|
Контрольная работа по дискретной математике.
Задание 1.
На рисунке изображен граф. Его дуги обозначены буквами a – p. Обозначить произвольным образом вершины графа. Взяв из таблицы вариантов данные о длине его дуг, определить:
1. Кратчайший путь из начальной вершины в конечную, и длину кратчайшего пути.
2. Критический путь из начальной вершины в конечную, и длину критического пути.
3. Считая этот граф сетевым графиком некоторого процесса, а длины дуг – временем осуществления работ, определить:
- для каждой вершины-события ранний и поздний срок его свершения и его резерв времени,
- для каждой дуги-работы независимый резерв времени.
 
Варианты:
| №
|
a
|
b
|
c
|
d
|
e
|
f
|
g
|
h
|
i
|
j
|
k
|
l
|
m
|
n
|
o
|
p
|
| 1
|
4
|
5
|
3
|
5
|
6
|
4
|
2
|
7
|
4
|
8
|
2
|
8
|
6
|
2
|
1
|
4
|
| 2
|
3
|
3
|
4
|
2
|
5
|
7
|
4
|
3
|
3
|
5
|
8
|
2
|
2
|
6
|
7
|
3
|
| 3
|
3
|
4
|
4
|
3
|
2
|
1
|
3
|
5
|
5
|
4
|
3
|
4
|
7
|
1
|
2
|
2
|
| 4
|
3
|
4
|
4
|
4
|
4
|
4
|
6
|
6
|
7
|
3
|
8
|
5
|
1
|
4
|
1
|
3
|
| 5
|
3
|
2
|
1
|
4
|
6
|
3
|
1
|
1
|
5
|
3
|
6
|
7
|
8
|
4
|
2
|
6
|
| 6
|
3
|
2
|
2
|
4
|
5
|
2
|
6
|
9
|
4
|
5
|
2
|
3
|
4
|
2
|
6
|
7
|
| 7
|
3
|
5
|
5
|
4
|
6
|
7
|
2
|
3
|
4
|
5
|
6
|
3
|
6
|
3
|
2
|
5
|
| 8
|
3
|
4
|
4
|
4
|
2
|
2
|
3
|
1
|
2
|
3
|
4
|
2
|
3
|
1
|
3
|
3
|
| 9
|
3
|
6
|
4
|
3
|
5
|
6
|
2
|
5
|
2
|
5
|
6
|
2
|
5
|
3
|
4
|
3
|
| 10
|
3
|
4
|
1
|
7
|
4
|
7
|
3
|
4
|
2
|
5
|
2
|
5
|
1
|
3
|
7
|
5
|
| 11
|
3
|
4
|
3
|
5
|
6
|
4
|
2
|
7
|
4
|
8
|
2
|
8
|
6
|
2
|
1
|
4
|
| 12
|
5
|
3
|
5
|
2
|
5
|
7
|
4
|
3
|
3
|
5
|
8
|
2
|
2
|
6
|
7
|
3
|
| 13
|
5
|
4
|
4
|
2
|
2
|
1
|
3
|
5
|
5
|
4
|
3
|
4
|
7
|
1
|
2
|
2
|
| 14
|
4
|
4
|
4
|
4
|
1
|
4
|
6
|
6
|
7
|
3
|
8
|
5
|
1
|
4
|
1
|
3
|
| 15
|
4
|
2
|
1
|
4
|
6
|
6
|
1
|
1
|
5
|
3
|
6
|
7
|
8
|
4
|
2
|
6
|
| 16
|
6
|
2
|
2
|
4
|
5
|
2
|
7
|
9
|
4
|
5
|
2
|
3
|
4
|
2
|
6
|
3
|
| 17
|
5
|
5
|
5
|
4
|
6
|
7
|
2
|
8
|
4
|
5
|
6
|
3
|
6
|
3
|
7
|
5
|
| 18
|
4
|
4
|
4
|
4
|
2
|
2
|
3
|
1
|
4
|
3
|
4
|
2
|
3
|
6
|
3
|
3
|
| 19
|
6
|
6
|
4
|
3
|
5
|
6
|
2
|
5
|
2
|
8
|
6
|
2
|
4
|
3
|
4
|
3
|
| 20
|
7
|
4
|
1
|
7
|
4
|
7
|
3
|
4
|
2
|
5
|
1
|
6
|
1
|
3
|
7
|
5
|
| 21
|
8
|
5
|
3
|
5
|
6
|
4
|
2
|
7
|
4
|
8
|
2
|
8
|
6
|
2
|
1
|
4
|
| 22
|
6
|
3
|
4
|
2
|
5
|
7
|
4
|
3
|
3
|
5
|
8
|
2
|
2
|
6
|
7
|
3
|
| 23
|
7
|
4
|
4
|
3
|
2
|
1
|
3
|
5
|
5
|
4
|
3
|
4
|
7
|
1
|
2
|
2
|
| 24
|
6
|
4
|
4
|
4
|
4
|
4
|
6
|
6
|
7
|
3
|
8
|
5
|
1
|
4
|
1
|
3
|
| 25
|
6
|
2
|
1
|
4
|
6
|
3
|
1
|
1
|
5
|
3
|
6
|
7
|
8
|
4
|
2
|
6
|
| 26
|
6
|
2
|
2
|
4
|
5
|
2
|
6
|
9
|
4
|
5
|
2
|
3
|
4
|
2
|
6
|
7
|
| 27
|
7
|
5
|
5
|
4
|
6
|
7
|
2
|
3
|
4
|
5
|
6
|
3
|
6
|
3
|
2
|
5
|
| 28
|
8
|
4
|
4
|
4
|
2
|
2
|
3
|
1
|
2
|
3
|
4
|
2
|
3
|
1
|
3
|
3
|
Задание 2.
Проект состоит из последовательного выполнения работ u1
, u2
, u3
, u4
.
Для каждой работы ui
( ) определена зависимость ее стоимости si
от времени ее осуществления ti
. ) определена зависимость ее стоимости si
от времени ее осуществления ti
.
1. Предполагая, что  , определить: , определить:
a) время осуществления работ  , для которых общая стоимость проекта , для которых общая стоимость проекта  минимальна при условии, что весь проект должен быть закончен не позднее времени Tmax
. Также найти при этих условиях минимальную стоимость проекта минимальна при условии, что весь проект должен быть закончен не позднее времени Tmax
. Также найти при этих условиях минимальную стоимость проекта  и стоимость осуществления каждой работы и стоимость осуществления каждой работы  . .
Значения
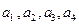 ,
Tmax
для каждого варианта даны в столбцах 2 - 6 таблицы вариантов
,
Tmax
для каждого варианта даны в столбцах 2 - 6 таблицы вариантов
б) стоимости работ 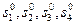 , для которых общее время осуществления проекта , для которых общее время осуществления проекта 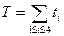 минимально при условии, что общая стоимость проекта не более Smax
. Также найти при этих условиях минимальное время осуществления проекта минимально при условии, что общая стоимость проекта не более Smax
. Также найти при этих условиях минимальное время осуществления проекта  и время осуществления каждой работы и время осуществления каждой работы  . .
Значения
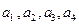 ,
Smax
для каждого варианта даны в столбцах 2 – 5 и 7 таблицы вариантов.
,
Smax
для каждого варианта даны в столбцах 2 – 5 и 7 таблицы вариантов.
2. Предполагая, что зависимость si
от ti
линейная и убывающая, и зная для каждой работы ui
ее минимальное и максимальное время осуществления 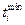 и и  , а также минимальную и максимальную стоимость , а также минимальную и максимальную стоимость  и и  определить: определить:
a) время осуществления работ  , для которых общая стоимость проекта , для которых общая стоимость проекта  минимальна при условии, что весь проект должен быть закончен не позднее времени Tmax
. Также найти при этих условиях минимальную стоимость проекта минимальна при условии, что весь проект должен быть закончен не позднее времени Tmax
. Также найти при этих условиях минимальную стоимость проекта  и стоимость осуществления каждой работы и стоимость осуществления каждой работы  . .
Значения
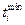 , ,  , ,
 , ,  , Tmax
для каждого варианта даны в столбцах 8 – 15 и 6 таблицы вариантов. , Tmax
для каждого варианта даны в столбцах 8 – 15 и 6 таблицы вариантов.
б) стоимости работ 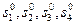 , для которых общее время осуществления проекта , для которых общее время осуществления проекта 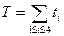 минимально при условии, что общая стоимость проекта не более Smax
. Также найти при этих условиях минимальное время осуществления проекта минимально при условии, что общая стоимость проекта не более Smax
. Также найти при этих условиях минимальное время осуществления проекта  и время осуществления каждой работы и время осуществления каждой работы  . .
Значения
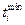 , ,  , ,
 , ,  , Smax
для каждого варианта даны в столбцах 8 – 15 и 7 таблицы вариантов. , Smax
для каждого варианта даны в столбцах 8 – 15 и 7 таблицы вариантов.
Варианты:
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
| №
вар-та.
|
a1
|
a2
|
a3
|
a4
|
Tmax
|
Smax
|
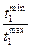
|
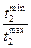
|

|

|

|

|
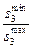
|

|
| 1
|
6
|
5
|
3
|
1
|
10
|
40
|

|

|
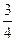
|
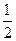
|

|

|
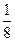
|
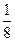
|
| 2
|
2
|
3
|
4
|
2
|
15
|
70
|
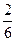
|

|

|

|

|

|

|
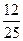
|
| 3
|
3
|
6
|
4
|
2
|
10
|
10
|
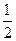
|
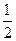
|

|
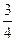
|

|

|

|
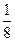
|
| 4
|
3
|
4
|
1
|
7
|
10
|
40
|

|
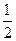
|

|

|

|

|

|
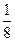
|
| 5
|
3
|
2
|
1
|
4
|
10
|
30
|
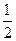
|

|
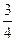
|

|

|

|

|
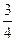
|
| 6
|
3
|
2
|
5
|
4
|
15
|
20
|
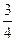
|

|

|

|

|

|
|

|
| 7
|
3
|
5
|
9
|
4
|
20
|
70
|

|

|

|
|
|

|

|

|
| 8
|
3
|
4
|
2
|
1
|
25
|
20
|
|

|

|

|

|

|
|

|
| 9
|
3
|
6
|
4
|
1
|
10
|
60
|

|
|

|

|

|

|

|

|
| 10
|
3
|
4
|
1
|
7
|
10
|
70
|

|

|

|

|

|

|
|

|
| 11
|
3
|
4
|
8
|
5
|
10
|
40
|

|

|
|

|

|

|

|
|
| 12
|
5
|
3
|
7
|
2
|
15
|
70
|

|

|

|

|

|

|
|

|
| 13
|
5
|
4
|
3
|
2
|
20
|
10
|

|

|
|

|

|

|

|
|
| 14
|
4
|
2
|
1
|
3
|
10
|
40
|
|

|

|
|

|

|

|

|
| 15
|
4
|
2
|
1
|
3
|
20
|
60
|
|

|

|

|

|

|
|
|
| 16
|
6
|
1
|
2
|
4
|
25
|
20
|

|

|
|

|

|

|

|
|
| 17
|
5
|
3
|
2
|
4
|
25
|
70
|

|
|
|

|

|

|

|

|
| 18
|
4
|
2
|
1
|
5
|
20
|
20
|

|
|
|

|

|

|

|

|
| 19
|
6
|
2
|
4
|
3
|
10
|
60
|

|
|

|

|

|

|

|

|
| 20
|
7
|
4
|
1
|
3
|
15
|
70
|
|

|

|

|

|

|

|

|
| 21
|
8
|
5
|
3
|
9
|
10
|
40
|
|

|

|

|

|

|

|

|
| 22
|
6
|
3
|
4
|
2
|
20
|
70
|

|

|

|
|

|

|

|

|
| 23
|
7
|
4
|
9
|
3
|
25
|
10
|

|

|

|

|

|

|

|

|
| 24
|
6
|
7
|
9
|
5
|
20
|
40
|

|

|

|

|

|

|

|

|
| 25
|
6
|
2
|
1
|
4
|
20
|
30
|
|

|

|

|

|

|
|

|
| 26
|
6
|
2
|
3
|
4
|
15
|
20
|

|

|

|

|

|

|
|
|
| 27
|
7
|
5
|
6
|
4
|
20
|
70
|

|

|
|
|

|

|

|

|
| 28
|
8
|
1
|
3
|
4
|
20
|
20
|

|

|

|

|

|

|

|

|
|

