|
Показатели вариации.
1. Понятие вариации и роль ее изучения в статистических исследованиях.
2. Измерители вариации.
3. Прямой способ расчета показателей вариации.
4. Свойства дисперсии и среднего квадратического отклонения.
5. Упрощенный способ расчета дисперсии и средне квадратического отклонения.
6. Относительные показатели вариации.
7. Стандартизация данных.
8. Моменты распределения.
9. Показатели асимметрии и эксцесса.
10. Средняя арифметическая и дисперсия альтернативного признака.
1. Понятие вариации и роль ее изучения в статистических исследованиях.
Вариация
– это колеблемость значений признака у отдельных единиц совокупности.
Наличию вариации обязана своим появлением статистика. Большинство статистических закономерностей проявляется через вариацию. Изучая вариацию значений признака в сочетании с его частотными характеристиками, мы обнаруживаем закономерности распределения (например: население по возрасту, студентов по уровню оценок).
Рассматривая вариацию одного признака параллельно с изменением другого, мы обнаруживаем взаимосвязи между этими признаками или их отсутствие (например: зависимость между торговой площадью и товарооборотом).
Вариации в статистике проявляются двояко, либо через изменения значений признака у отдельных единиц совокупности, либо через наличие или отсутствие изучаемого признака у отдельных единиц совокупности.
Изучение вариации в статистике имеет как самостоятельную цель, так и является промежуточным этапом более сложных статистических исследований.
2. Измерители вариации.
Простейшим показателем вариации является размах колебаний
: 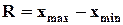 . .
Достоинство этого показателя простота расчета, возможность использования для оценки вариации однородных совокупностей. Недостаток – неприемлемость для неоднородных совокупностей с редкими выбросами крайних значений признака.
Частично недостатки этого показателя устраняет межквартельный размах
:  . Однако, он характеризует вариацию только половины совокупности. . Однако, он характеризует вариацию только половины совокупности.
Для учета колеблемости всех значений признака применяют показатели среднего линейного отклонения, дисперсии и средне квадратического отклонения.
Средне линейное отклонение
– среднее значение отклонений всех вариантов ряда от средней арифметической (иногда от моды или медианы):
 - для несгруппированных данных; - для несгруппированных данных;
 - для сгруппированных данных. - для сгруппированных данных.
 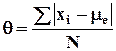
Аналогичным по смыслу среднему линейному отклонению является показатель дисперсии и рассчитываемый на его основе показатель средне квадратического отклонения.
Дисперсия
– рассеивание, данный показатель характеризует рассеивание значений признака относительно его средней величины.
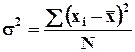 - для несгруппированных данных; - для несгруппированных данных;
 - для сгруппированных данных. - для сгруппированных данных.
Дисперсия
– средне квадратическое отклонение всех вариантов ряда от средней арифметической. Если извлечь квадратный корень из дисперсии, получим средне квадратическое отклонение
.
 - для несгруппированных данных; - для несгруппированных данных;
 - для сгруппированных данных. - для сгруппированных данных.
Несмотря на логическое сходство, дисперсия является более чувствительной к вариации и, следовательно, чаще применяемый показатель.
3. Прямой способ расчета показателей вариации.
Расчет показателей вариации
заработной платы работников завода.
| Группы со среднемесячной з/п, руб.
|
Число раб-в, 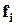
|

|

|

|

|

|

|
| До 1500
|
30
|
750
|
22500
|
1909,09
|
57272,7
|
3644628
|
109338843
|
| 1501-3000
|
75
|
2250
|
168750
|
409,09
|
30681,8
|
167355
|
12551653
|
| 3001-4500
|
45
|
3750
|
168750
|
1090,91
|
49090,9
|
1190083
|
53553719
|
| Свыше 4501
|
15
|
5250
|
78750
|
2590,91
|
38863,6
|
6712810
|
100692149
|
| Итого
|
165
|
|
438750
|
|
175909
|
|
276136364
|
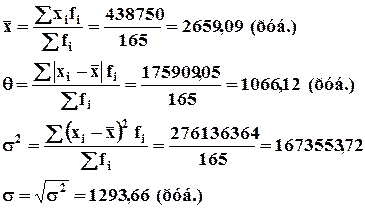
Заработная плата каждого из работников в среднем отклоняется от средне заработной платы на 1066,12 руб.
Средне квадратическое отклонение  заметно больше, чем аналогичный ему по смыслу среднее линейное отклонение. заметно больше, чем аналогичный ему по смыслу среднее линейное отклонение.
4. Свойства дисперсии и среднего квадратического отклонения.
Так же как и средняя дисперсия обладает рядом свойств, имеющих важное значение для понимания сущности этого показателя, методологии его расчета и практического использования для разработки более совершенных статистических методов.
Свойства дисперсии и средне квадратическое отклонение:
1) Если все варианты ряда уменьшить или увеличить на постоянное число, то величина дисперсии и средне квадратического отклонения не изменится.  ; ;
2) Если все варианты ряда умножить или разделить на постоянное число, дисперсия соответственно увеличится или уменьшится в квадрат этого числа раз, а средне квадратическое отклонение в это число раз.  ; ;
3) Если частоты ряда уменьшить или увеличить в постоянное число раз, то дисперсия и средне квадратическое отклонение от этого не изменится;
4) Дисперсия равна среднему квадрату вариантов ряда минус квадрат средней арифметической. 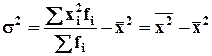 ; ;
5) Общая дисперсия равна средней арифметической из частных дисперсий (внутригрупповых дисперсий) плюс дисперсии частных средних (межгрупповые дисперсии). Это свойство называется правилом сложения дисперсий
, которое широко применяется в выборочном методе, методе измерений взаимосвязей явлений, а так же дисперсионном анализе.
 - общая дисперсия; - общая дисперсия;
 - частная дисперсия; - частная дисперсия;
 - средняя из частных дисперсий, - средняя из частных дисперсий,  - численность соответствующей группы; - численность соответствующей группы;
 - межгрупповая дисперсия; - межгрупповая дисперсия;

5. Упрощенный способ расчета дисперсии и средне квадратического отклонения.
Свойства дисперсии используются для упрощения методики ее расчета. В условиях развитой вычислительной техники данный способ имеет, прежде всего, иллюстративный характер и помогает понять сущность этого показателя.
Упрощенный способ расчета дисперсии и средне квадратического отклонения (метод расчета от условного нуля).
| Среднемесячная з/п работников, руб., 
|
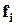
|

|

|
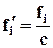
|

|
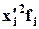
|
| 750
|
30
|
- 1 500
|
-1
|
2
|
-2
|
2
|
| 2 250
|
75
|
0
|
0
|
5
|
0
|
0
|
| 3 750
|
45
|
1 500
|
1
|
3
|
3
|
3
|
| 5 250
|
15
|
3 000
|
2
|
1
|
2
|
4
|
| Итого
|
|
|
|
11
|
3
|
9
|
А=2250; k=1500; с=15

6. Относительные показатели вариации.
Абсолютные измерители вариации (дисперсия, средне квадратическое отклонение) ограниченно пригодны для сравнительного анализа вариаций различных совокупностей.
Для цели сравнительного анализа применяют относительные показатели, коэффициенты вариации
. Наиболее распространенной формой коэффициентов вариации является 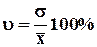 , он показывает, какой процент от средней арифметической составляет среднее квадратическое отклонение. , он показывает, какой процент от средней арифметической составляет среднее квадратическое отклонение.
Вместо средне квадратического в числителе коэффициента вариации иногда используют среднее линейное отклонение  . .
Если среднее линейное отклонение определялось относительно медианы или моды, то соответствующие показатели вариации будут выглядеть  , ,  . .
Коэффициенты вариации определенные по различным основаниям не одинаковы, поэтому, сопоставляя вариации разных совокупностей, нужно использовать коэффициенты вариации, рассчитанные по одной и той же величине.
Коэффициент вариации является так же количественной мерой однородности совокупности. Принято считать, что если  , то совокупность количественно однородна. Чем меньше, тем лучше. , то совокупность количественно однородна. Чем меньше, тем лучше.
7. Стандартизация данных.
Коэффициенты вариации являются сводными оценками вариаций различных совокупностей. Однако они не позволяют сопоставить между собой значения признака у отдельных или групп единиц разных совокупностей.
Для подобных сравнений прибегают к стандартизации вариантов разных совокупностей по формулам:
 , где , где 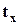 , , 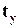 - это стандартизированные значения вариантов ряда x и y соответственно. В процессе стандартизации мы переходим от измерения вариантов в натуральных или стоимостных единицах к их измерению величинами соответствующих средне квадратических отклонений. - это стандартизированные значения вариантов ряда x и y соответственно. В процессе стандартизации мы переходим от измерения вариантов в натуральных или стоимостных единицах к их измерению величинами соответствующих средне квадратических отклонений.
Пример
: Стандартизация данных о доходах на одного члена семьи и среднедушевом потреблении мяса.
| Доход на
одного
члена семьи,
тыс. руб./год, 
|
Среднедушевое потребление
мяса, 
|

|
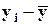
|

|

|
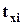
|

|
| 60,7
|
12,3
|
-97,5
|
-25,6
|
9 506,25
|
655,36
|
-1,28
|
-1,31
|
| 84,2
|
19,1
|
-74
|
-18,8
|
5 476,00
|
353,44
|
-0,97
|
-0,96
|
| 112,4
|
23,1
|
-45,8
|
-14,8
|
2 097,64
|
219,04
|
-0,60
|
-0,76
|
| 144,5
|
35,6
|
-13,7
|
-2,3
|
187,69
|
5,29
|
-0,18
|
-0,12
|
| 180,1
|
49,5
|
21,9
|
11,6
|
479,61
|
134,56
|
0,29
|
0,59
|
| 240,9
|
57,3
|
82,7
|
19,4
|
6 839,29
|
376,36
|
1,09
|
0,99
|
| 284,6
|
68,4
|
126,4
|
30,5
|
15 976,96
|
930,25
|
1,66
|
1,56
|
| 1107,4
|
265,3
|
|
|
40 563,44
|
2 674,30
|
|
|
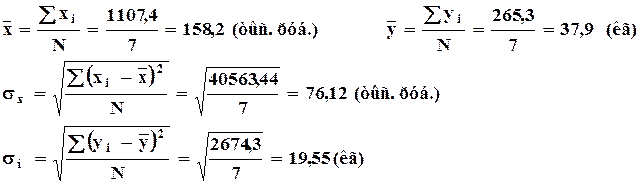

При стандартизации сгруппированных данных наряду с масштабированием вариантов ряда величинами соответствующих средне квадратических отклонений частоты этих рядов пересчитываются в частости.
Стандартизацию данных проводят, когда варианты сравниваемых рядов отличаются единицами измерения и порядком.
Стандартизация является важнейшим статистическим промежуточным этапом.
Стандартизация используется так же хорошо в теории выборочного метода.
8. Моменты распределения.
Моменты распределения
составляют алгоритмическую основу многих статистических методов. Различают:
- Произвольные (общий случай);
- Начальные;
- Центральные;
- Стандартные (частный случай).
Выделяют:
- Взвешенные;
- Невзвешенные.
Произвольным моментом
k
-го порядка
называется среднее значение k-ой степени отклонения всех вариантов ряда от произвольного постоянного числа.
 - для несгруппированных данных; - для несгруппированных данных;
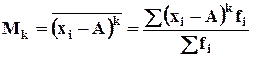 - для сгруппированных данных. - для сгруппированных данных.
При этом k принимает целочисленное значение от 1 до 4.
Если А=0
, то произвольный момент преобразуется в начальный момент
.
 - для несгруппированных данных; - для несгруппированных данных;
при k=1 M1
=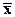
при k=2 M2
=
 - для сгруппированных данных. - для сгруппированных данных.
Если А=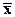 , произвольный момент преобразуется в центральный момент распределения
. , произвольный момент преобразуется в центральный момент распределения
.
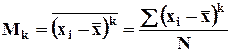 - для несгруппированных данных; - для несгруппированных данных;
 - для сгруппированных данных. - для сгруппированных данных.
При k=1 M1
=0
При k=2 M2
=
Стандартные моменты
это начальные моменты из стандартных отклонений.
 - для несгруппированных данных; - для несгруппированных данных;
 - для сгруппированных данных. - для сгруппированных данных.

Стандартный момент k-го порядка это отношение центрального момента того же порядка к средне квадратическому отклонению в k-ой степени.
Так же как средняя арифметическая величина и дисперсия, центральные и стандартные моменты обладают рядом свойств, которые по сути ближе всего к свойствам дисперсии.
9. Показатели асимметрии и эксцесса.
При анализе распределений помимо графического изображения характер распределения можно выяснить, рассчитывая такие показатели, как асимметрия и эксцесс.
В качестве показателя асимметрии
используют стандартный момент 3-го порядка. Если распределение симметрично относительно средней то показатель асимметрии равен нулю.
 
Если показатель асимметрии больше 0, то есть преобладают положительные отклонения от среднего, то наблюдается правосторонняя асимметрия
, то есть преобладание в совокупности вариантов ряда превышающих среднюю.
Если же показатель асимметрии меньше 0, налицо левосторонняя асимметрия
, то есть превышение численности вариантов ряда меньше чем средняя.
Показатель эксцесса
характеризует степень колеблемости исходных данных, чем сильнее вариация, тем более пологой является кривая распределения и наоборот, чем однороднее совокупность, тем в большей степени варианты ряда сконцентрированы около средней и тем более островершинней будет кривая распределения.
В качестве эталона высоты распределения в статистике принимается кривая нормального распределения. Доказано, что стандартный момент 4-го порядка у этой кривой равен 3.
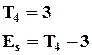 
10. Средняя арифметическая и дисперсия альтернативного признака.
Альтернативный признак
– тот которым обладает или не обладает единица совокупности.
Наличие альтернативного признака обозначают 1, а отсутствие – 0. Если численность совокупности – N, а M – число единиц, обладающих изучаемым признаком, то  - доля единиц, обладающих изучаемым признаком. Соответственно - доля единиц, обладающих изучаемым признаком. Соответственно  - доля единиц таким признаком не обладающих. - доля единиц таким признаком не обладающих.
Предположим
| 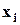
|
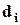
|
| 1
|
p
|
| 0
|
q
|
| |
1
|
p+q=1
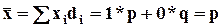
Средняя арифметическая альтернативного признака равна p.

Дисперсия альтернативного признака 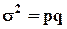 . .
Пример
: N=10, M=4
N-M=6
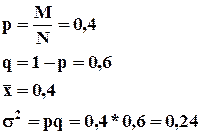
Максимальное значение дисперсии для неоднородных совокупностей  . .
|