| ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Амурский государственный университет»
(ГОУВПО «АмГУ»)
Кафедра энергетики
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА
на тему: "Расчёт и оценка надёжности электрических сетей"
по дисциплине "Надежность электроэнергетических систем и сетей"
Благовещенск 2006
Задание 1
Рассчитать надёжность схемы внутреннего электроснабжения насосной станции двумя методами.
| 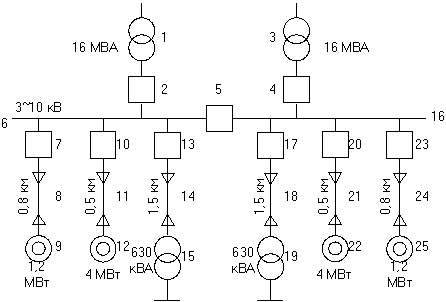
Рисунок 1 – Исходная схема к расчёту надёжности
|
|
1) Определим расчётные случаи по надёжности, предварительно составив расчётную схему для рассматриваемой сети (рис. 2). Разъединители учитываем в модели выключателя.
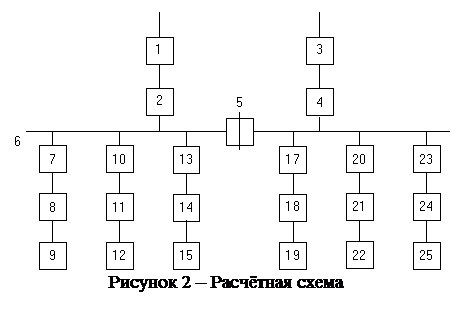
В данной сети расчётными будут являться случаи: полное погашение подстанции и потеря трансформатора.
2) Определим показатели надёжности каждого элемента.
Таблица 1-Показатели надёжности элементов сети
| Элементы
|
 , 1/год , 1/год
|
Тв
, ч
|
 , 1/год , 1/год
|
Тр
, ч
|
акз
|
ао.п.
|
| Выключатели
|
0,009
|
20
|
0,14
|
8
|
0,005
|
0,003
|
| Разъединители
|
0,01
|
7
|
0,166
|
3,7
|
-
|
-
|
| Шины
|
0,03
|
7
|
0,166
|
5
|
-
|
-
|
| Силовые трансформаторы
|
0,014
|
70
|
0,75
|
28
|
-
|
-
|
| Трансформаторы
|
0,016
|
50
|
0,25
|
6
|
-
|
-
|
| Кабельная линия
|
0,075
|
16
|
1
|
2
|
-
|
-
|
| Насосы
|
1,2 МВт
|
0,1
|
90
|
0,25
|
164
|
-
|
-
|
| 4 МВт
|
0,2
|
140
|
0,25
|
384
|
-
|
-
|
Релейные защиты, отключающие выключатели расчётной схемы:
- для ВЛ-10: дистанционная ПЗ 2, т. к. не имеем данных для токовой трёхступенчатой защиты;
- для СТ: дифференциальная и газовая защиты;
- на схеме «мостик» со стороны 10 кВ введено АВР;
- шины 10 кВ защищены дифференциальной защитой шин.
Укажем показатели надёжности для релейных защит в таблице 2.
Таблица 2 – Показатели надёжности для выделенных защит
| Релейная защита
|
q
|
| Дистанционная ПЗ2
|
0,018
|
| ДЗТ
|
0,0044
|
| Газовая защита
|
0,00525
|
| ДЗШ
|
0,0096
|
3) Составляем схему замещения согласно правилам:
1 Нерезервируемые элементы соединяются последовательно;
2 Резервируемые элементы соединяются параллельно.
Укажем варианты схемы в соответствии с расчётными случаями, найденными ранее:
Первый вариант – полное погашение подстанции.
| 
Рисунок 3
|
|
Второй вариант – потеря трансформатора (частичное ограничение мощности).
| 
Рисунок 4
|
|
4) Рассмотрим первый вариант.
Находим вероятности отказа для различных элементов:
Выключатели:
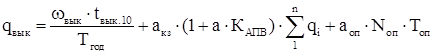
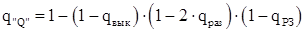 , ,
где акз
– относительная частота отказа выключателя при отключении КЗ;
а – коэффициент, учитывающий наличие (а = 1), отсутствие АПВ (а = 0);
КАПВ
– коэффициент успешного действия АПВ;
qi
– вероятность отказа смежных элементов;
аоп
– частота отказов при оперативном отключении;
Nоп
число оперативных отключений: 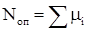 ; ;
Топ
– время оперативных переключений. Принимаем его равным 1 часу.
Разъединители:
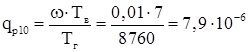
Шины:
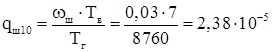
Силовые трансформаторы:
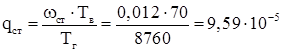
Трансформаторы:
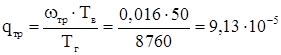
Кабельная линия:
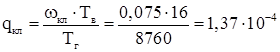
Насосы:
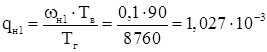

Эквивалентирование схемы показано в приложении А.
Как видно из него, qэкв
= 0,0087, pэкв
= 0,91.
Вероятность отказа схемы с учетом средств автоматики рассмотрим для участка схемы, показанного на рисунке 5.
| 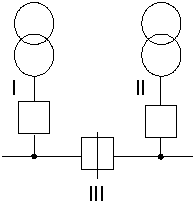
Рисунок 5
|
|
Вероятность отказа рассчитываем по формуле полной вероятности:
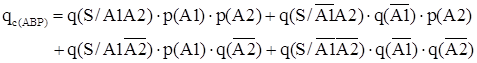
где 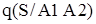 - условная вероятность отказа системы, при отсутствии отка- - условная вероятность отказа системы, при отсутствии отка-
зов средств автоматики или qэкв
;
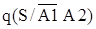 - условная вероятность при условии неуспешного автоматического отключения повреждённого элемента и отсутствии отказа во включении резервного, - условная вероятность при условии неуспешного автоматического отключения повреждённого элемента и отсутствии отказа во включении резервного,
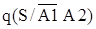 = 0,5; = 0,5;
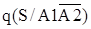 - условная вероятность при условии успешного автоматического отключения повреждённого элемента и отказа во включении резервного - условная вероятность при условии успешного автоматического отключения повреждённого элемента и отказа во включении резервного 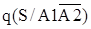 =0,5; =0,5;
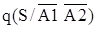 - условная вероятность при условии неуспешного автоматического отключения повреждённого элемента и отказа во включении резервного - условная вероятность при условии неуспешного автоматического отключения повреждённого элемента и отказа во включении резервного 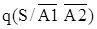 = 0,5; = 0,5;
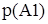 – вероятность безотказной работы при автоматическом отключении поврежденного элемента; – вероятность безотказной работы при автоматическом отключении поврежденного элемента;
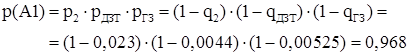
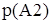 – вероятность безотказной работы при автоматическом включении резервного элемента; – вероятность безотказной работы при автоматическом включении резервного элемента;
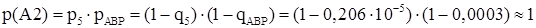
q(A1) – вероятность отказа работы при автоматическом отключении поврежденного элемента
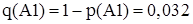 ; ;
q(A2) – вероятность отказа работы при автоматическом включении резервного элемента;
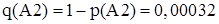
Получаем вероятность отказа схемы с учетом РЗиА:
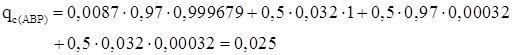
Задание 2
Записать систему дифференциальных уравнений на основе графа перехода из состояния в состояние для трёх параллельно соединённых элементов и показать чему равны стационарные КГ
, КП
.
| 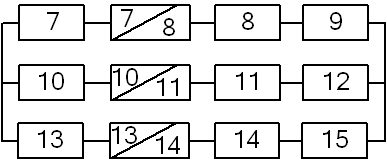
Рисунок 6
|
|
Решение
:
Сэквивалентируем элементы во второй и третьей ветвях до одного элемента (рис. 7). На этом же рисунке покажем все возможные состояния, в которых могут находиться элементы схемы (р – работа, о – отказ).
| 
Рисунок 7
|
|
Составим граф перехода со всеми возможными переходами из одного состояния в другое (рис. 8). Интенсивность восстановления μ на рисунке не показываем для того, чтобы его не загромождать. μ будут иметь обратные направления по отношению к параметру потока отказов ω, индекс у них будет тот же, что и у ω.
| 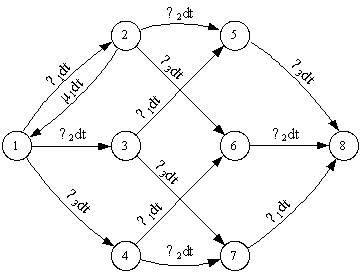
Рисунок 8 - Граф перехода
|
|
Система дифференциальных уравнений для полученного графа будет иметь вид:
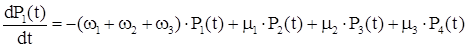 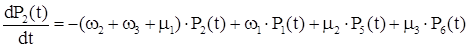
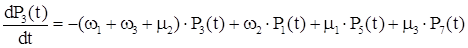
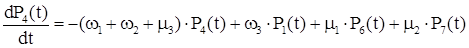
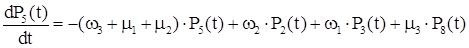
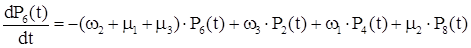
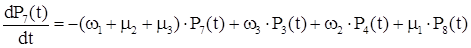
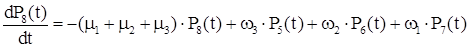
Для стационарного состояния эта система имеет следующее решение:
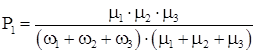
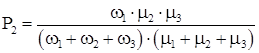
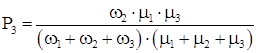
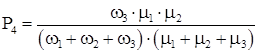
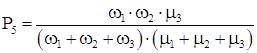
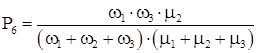
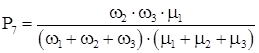
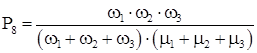
Для стационарного состояния коэффициенты готовности КГ
и простоя КП
находятся по формулам:
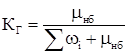
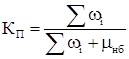
Для нашего случая:
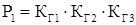 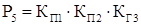
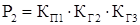 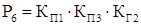
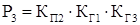 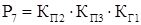
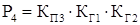 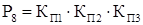
Из полученных выражений для вероятностей состояний системы определяются коэффициент готовности системы КГ.С
и коэффициент вынужденного простоя КП.С
.
КГ.С
= P1
+P2
+P3
+P4
+P5
+P6
+P7
КП.С
= P8
Задание 3
Определить кратность резервирования для схемы при условии, что есть резервные насосы 4 МВт и 1,2 МВт и определить при этом вероятность безотказной работы насосной станции.
Решение
:
Из условия видим, общее число насосов равно n = 6, в работе находятся четыре, r = 4. Число резервных элементов – (n-r) = 2.
Кратность резервирования в этом случае определится по формуле:
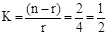
Как видим из формулы, чем большая кратность резервирования, тем лучше, т. к. чем больший резерв имеется в системе, тем безопасней её работа, а значит и надёжность работы такой системы выше.
Вероятность безотказной работы системы с постоянным резервом при заданных условиях рассчитывается по формуле:
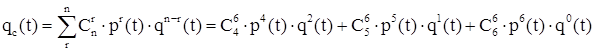 где где 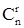 - число сочетаний из n-элементов по r: - число сочетаний из n-элементов по r: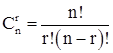 . .
Приняв из задания 1 qэкв
= 0,0087, pэкв
= 0,91, получим значение для вероятности безотказной работы насосной станции:
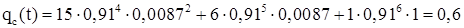
|