СОДЕРЖАНИЕ
СОДЕРЖАНИЕ................................................................................................................................
3
ВВЕДЕНИЕ....................................................................................................................................... 4
ОБОСНОВАНИЕ ВЫБОРА ТИПА МОДЕЛИ........................................................................... 5
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ МОДЕЛИ............................................................................. 7
РАСЧЕТ ХАРАКТЕРИСТИК МОДЕЛИ................................................................................... 9
Расчет характеристик для М=1...................................................................................................... 9
Расчет характеристик для М=3.................................................................................................... 12
Расчет характеристик для М=5.................................................................................................... 14
Определение оптимальных значений
быстродействия устройств........................................................................................ 16
Построение графических зависимостей.......................................................... 18
Анализ полученных результатов............................................................................ 20
Список литературы............................................................................................................ 21
Очень часто на практике встречаются объекты, в которых заявка проходит обслуживание в определенной последовательности во многих устройствах. В качестве модели таких объектов обычно выбирают сетевые модели (СМ).
В этом случае модель вычислительной системы (ВС) представляется как совокупность взаимосвязанных систем массового обслуживания (СМО), для описания процессов функционирования которых используются модели теории массового обслуживания.
Обычно сетевые модели ВС широкого класса строятся из набора типовых СМО: одно- и многоканальных. В этот набор могут входить СМО, имитирующие обслуживание заявок различными элементами аппаратного и программного обеспечения ВС, в частности устройствами типа процессор, оперативная память, селекторный канал, а также элементами, служащими источниками и приёмниками заявок. Т. о. Каждая СМО ставится в соответствие какому-то устройству реального объекта.
Различают разомкнутые и замкнутые сети. В разомкнутых сетях заявки поступают из внешнего источника. Интенсивность этого источника не зависит от состояния сети, т. е. от количества заявок уже поступивших в сеть. Для замкнутых сетей характерным является постоянство числа циркулирующих в них заявок (внешние источники в замкнутых сетях отсутствуют).
Разомкнутые сети обычно используются в качестве модели систем оперативной обработки (СОО), а замкнутые – как модели систем пакетной обработки (СПО).
В рамках данной курсовой работы будет выполнено моделирование системы пакетной обработки.
Определим модель системы пакетной обработки. СПО – ВС, выполнение работ в которых организуется путем загрузки в систему пакета задач, обрабатываемых в порядке ориентированном на минимизацию времени обработки всего пакета.
После ввода пакета ВС выполняет работы из него. При этом все прочие работы ожидают момента завершения обработки пакета. Следовательно, в качестве модели СПО выберем замкнутую СМ, так как в замкнутых СМ число заявок, циркулирующих в них, всегда постоянно.
В замкнутой СМ выделяется дуга, по которой заявка, соответствующая завершенной работе, инициирует заявку на выполнение новой работы. Обычно такая дуга помечается точкой «0». Условно эту систему называют нулевой системой. Время обслуживания заявки в нулевой системе равно 0. Количество заявок, проходящих в сети по отмеченной дуге за единицу времени, определяет производительность 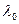 СПО. Значение СПО. Значение 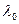 не зависит от каких-либо внешних причин, а определяется конфигурацией и параметрами сети. не зависит от каких-либо внешних причин, а определяется конфигурацией и параметрами сети.
Вся информация, относящаяся к пакету, вводится в память до начала его решения. Тогда за время решения пакета основной поток запросов формируется на обработку и обращения к ВЗУ. Т. е. процесс решения задачи представляется произвольной последовательностью этапов счета и обращений к файлам. Множество файлов 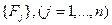 , используемых в процессе решения задач, размещается во внешней памяти системы. В рамках данного курсового проекта предполагается, что внешняя память ВС может состоять из накопителей двух типов: НМЛ и НМД. , используемых в процессе решения задач, размещается во внешней памяти системы. В рамках данного курсового проекта предполагается, что внешняя память ВС может состоять из накопителей двух типов: НМЛ и НМД.
Вследствие того, что к различным файлам производится разное число обращений при решении задач, естественно предположить, что файлы, сравнительно редко используемые в процессе решения задач, могут располагаться как в НМЛ, так и в НМД, в то время как файлы, частота обращений к которым велика, должны размещаться в НМД как устройствах внешней памяти с меньшим временем доступа.
Определим суммарный объем файлов G
с которыми работает система:
 Т. к. суммарный объем G
не превышает емкость НМД, то в систему будут включен единственный НМД, на котором расположены файлы F1
, F2
, F8
.
В качестве модели НМД будем использовать одноканальную СМО.
Для пересылки данных из ВЗУ в ОП используется селекторный канал (СК), к которому подключается ВЗУ (НМД). В качестве модели СК используется одноканальная СМО со своей очередью. Тогда схема модели системы пакетной обработки будет иметь вид, представленный на рис.1, где:
П-ОП – процессор и оперативная память;
НМД – накопитель на магнитном диске;
СК – селекторный канал.
Построим граф модели СПО:
S
1
– СМО моделирует П-ОП S
2
- СМО моделирует НМД
S3
- СМО моделирует СК
К параметрам модели относятся следующие величины:
1.
Число
N
систем массового обслуживания.
Из приведенной выше схемы модели СПО следует, что N=3.
2.
Число каналов, входящих в каждую СМО.
В нашей модели все СМО являются одноканальными, следовательно:

3.
Матрица вероятностей передач
P
=|
 |
|
где  - вероятность того, что заявка, покидающая систему
- вероятность того, что заявка, покидающая систему  , поступит в систему , поступит в систему 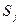 (i, j = 1,..,3). (i, j = 1,..,3).
Подсчитаем вероятности переходов системы. Очевидно, что: Чтобы найти вероятности остальных передач, найдем суммарное число обращений к файлам Q:
Тогда:
Так как:
То: 4.
Число М заявок, циркулирующих в замкнутой сети:
M=1,3,5.
5.
Средние длительности обслуживания заявок  одним каналом в системах одним каналом в системах  . .
Для расчета некоторых  нам понадобятся значения коэффициентов передач.
нам понадобятся значения коэффициентов передач.
где: n – число файлов; 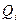 - число обращений к файлу - число обращений к файлу 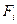 ; ; 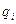 - средняя длина записи файла - средняя длина записи файла 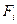 ; ;  -быстродействие устройства, в нашем случае -быстродействие устройства, в нашем случае  = =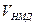 . .
1.
Определим значения коэффициентов передач  для всех СМО сети из следующей системы уравнений. для всех СМО сети из следующей системы уравнений.
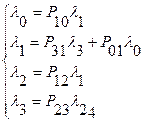 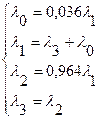 
Коэффициент передачи 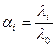 определяется относительно нулевой системы. Из системы уравнений следует: определяется относительно нулевой системы. Из системы уравнений следует:

Как видим, значение  совпадает с числом этапов обслуживания в i – ой системе, которое проходит каждая заявка, поступающая в СПО, т. е. равно среднему числу обращений к i – му устойству при выполнении одной задачи. совпадает с числом этапов обслуживания в i – ой системе, которое проходит каждая заявка, поступающая в СПО, т. е. равно среднему числу обращений к i – му устойству при выполнении одной задачи.
Теперь можно определить время обслуживания заявки в процессоре. Оно определяется как среднее арифметическое от времени обслуживания заявки в каждой из СМО с учетом коэффициентов передач: 2.
Определение вероятности состояний  . .
Вероятности состояний замкнутой сети определяются следующим выражением:
 (1) (1)
где:
Здесь Ki
– число каналов (приборов) в i-й системе. Символ  означает, что суммирование производится по всем возможным наборам mi
,…, mN
, для которых выполняется условие означает, что суммирование производится по всем возможным наборам mi
,…, mN
, для которых выполняется условие  . mi
– говорит о том, что в i – ом узле m заявок. M=1, число СМО N=3, тогда число возможных состояний найдем как: . mi
– говорит о том, что в i – ом узле m заявок. M=1, число СМО N=3, тогда число возможных состояний найдем как:
Перечислим эти состояния: (1,0,0), (0,1,0), (0,0,1).  для всех i=1..3, так как все СМО у нас одноканальные. для всех i=1..3, так как все СМО у нас одноканальные.
Для вычисления вероятностей возможных состояний нам в дальнейшем потребуются значения произведений 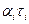 в соответствующих степенях: в соответствующих степенях:
| Устройство
|

|

|
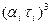
|

|
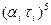
|
| П-ОП (
i=1
)
|
1,3664
|
1,867
|
2,551
|
3,4859
|
4,7631
|
| НМД (
i=2
)
|
1,89
|
3,5721
|
6,7513
|
12,76
|
24,1162
|
| СК (
i=3
)
|
0,8438
|
0,7119
|
0,6007
|
0,507
|
0,4276
|
Теперь отдельно вычислим знаменатель выражения (1):

Тогда: 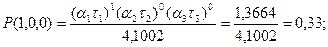
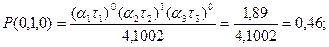
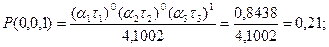
3.
Определение коэффициентов загрузки  каждой из СМО. каждой из СМО.
Для М=1 имеем, что 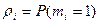 , тогда: , тогда:
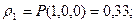 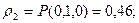 
4.
Определение интенсивности 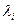 входного потока заявок
i
-й СМО. входного потока заявок
i
-й СМО.
Интенсивность входного потока – это число заявок, поступающих в единицу времени на вход соответствующей СМО.
Общая формула для расчета: 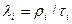 . .
Найдем 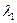 :
: 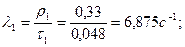
Остальные 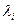 найдем через коэффициенты передач:
найдем через коэффициенты передач: 

5.
Определение времени цикла замкнутой сети.
Время цикла относительно i – ого узла – это среднее время от момента входа (выхода) одной и той же заявки в этот i – ый узел. Общая формула:
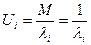 . .
Определим время цикла для нулевой системы:

6.
Определение среднего числа заявок
mi
в каждой СМО.
Общая формула для расчета: 
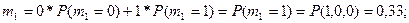
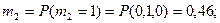 
1.
Определение вероятности состояний  . .
Число заявок в системе M=3, число СМО N=3, тогда число возможных состояний найдем как: Перечислим эти состояния: (3,0,0), (2,1,0), (2,0,1), (1,2,0), (1,1,1), (1,0,2), (0,3,0), (0,2,1), (0,1,2), (0,0,3).
 для всех i=1..3, так как все СМО у нас одноканальные. для всех i=1..3, так как все СМО у нас одноканальные.
Теперь отдельно вычислим знаменатель выражения (1):

Вероятности всех состояний представим в виде таблицы, опустив множество формул их определения:
| Вероятности
|
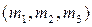
|

|
P1
|
(3,0,0)
|
0,0967
|
| P2
|
(2,1,0)
|
0,1338
|
| P3
|
(2,0,1)
|
0,0597
|
| P4
|
(1,2,0)
|
0,1851
|
| P5
|
(1,1,1)
|
0,0437
|
| P6
|
(1,0,2)
|
0,0369
|
| P7
|
(0,3,0)
|
0,256
|
| P8
|
(0,2,1)
|
0,1143
|
| P9
|
(0,1,2)
|
0,051
|
| P10
|
(0,0,3)
|
0,0228
|
2.
Определение коэффициентов загрузки 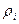 каждой из СМО. каждой из СМО.
Коэффициент загрузки здесь удобнее определять через коэффициент простоя. Коэффициент простоя hi
для каждой из одноканальных систем сети вычисляется суммированием по всем разложениям М вероятностей (1), для которых mi
=0, т.е. суммированием всех вероятностей простоя i-й системы: 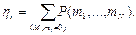
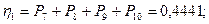
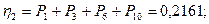

Тогда по формуле: 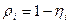 определим все коэффициенты загрузки. определим все коэффициенты загрузки.
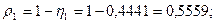 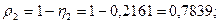

3.
Определение интенсивности 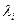 входного потока заявок
i
-й СМО. входного потока заявок
i
-й СМО.
Общая формула для расчета:  . .
Найдем 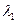 :
: 
Остальные 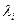 найдем через коэффициенты передач:
найдем через коэффициенты передач:


4.
Определение времени цикла замкнутой сети.
Общая формула:  . Определим время цикла для нулевой системы: . Определим время цикла для нулевой системы:
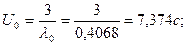
5.
Определение среднего числа заявок
mi
в каждой СМО.
Общая формула для расчета: 


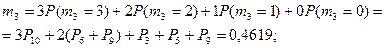
1.
Определение вероятности состояний  . .
Число заявок в системе M=5, число СМО N=3, тогда число возможных состояний найдем как:
Перечислим эти состояния: (5,0,0), (4,1,0), (4,0,1),(3,2,0), (3,1,1), (3,0,2), (2,3,0), (2,2,1), (2,1,2), (2,0,3), (1,4,0), (1,3,1), (1,2,2), (1,1,3), (1,0,4), (0,5,0), (0,4,1), (0,3,2), (0,2,3), (0,1,4), (0,0,5).  для всех i=1..3, так как все СМО у нас одноканальные. для всех i=1..3, так как все СМО у нас одноканальные.
Теперь найдем отдельно знаменатель выражения (1):

Вероятности всех состояний представим в виде таблицы, опустив множество формул их определения:
| Вероятности
|
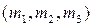
|

|
P1
|
(5,0,0)
|
0,038
|
| P2
|
(4,1,0)
|
0,0526
|
| P3
|
(4,0,1)
|
0,0235
|
| P4
|
(3,2,0)
|
0,0727
|
| P5
|
(3,1,1)
|
0,0325
|
| P6
|
(3,0,2)
|
0,0145
|
| P7
|
(2,3,0)
|
0,1006
|
| P8
|
(2,2,1)
|
0,0449
|
| P9
|
(2,1,2)
|
0,02
|
| P10
|
(2,0,3)
|
0,0089
|
| P11
|
(1,4,0)
|
0,1392
|
| P12
|
(1,3,1)
|
0,0621
|
| P13
|
(1,2,2)
|
0,0277
|
| P14
|
(1,1,3)
|
0,0124
|
| P15
|
(1,0,4)
|
0,0055
|
| P16
|
(0,5,0)
|
0,1925
|
| P17
|
(0,4,1)
|
0,0859
|
| P18
|
(0,3,2)
|
0,0384
|
| P19
|
(0,2,3)
|
0,0171
|
| P20
|
(0,1,4)
|
0,0076
|
| P21
|
(0,0,5)
|
0,0034
|
2.
Определение коэффициентов загрузки 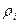 каждой из СМО. каждой из СМО.
Коэффициент загрузки здесь удобнее определять через коэффициент простоя. Коэффициент простоя h
i
для каждой из одноканальных систем сети вычисляется суммированием по всем разложениям М вероятностей (1), для которых mi
=0, т.е. суммированием всех вероятностей простоя i-й системы: 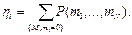
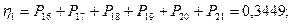


Тогда по формуле: 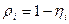 определим все коэффициенты загрузки. определим все коэффициенты загрузки.
 

3.
Определение интенсивности  входного потока заявок
i
-й СМО. входного потока заявок
i
-й СМО.
Общая формула для расчета:  . .
Найдем  :
: 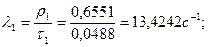
Остальные  найдем через коэффициенты передач:
найдем через коэффициенты передач:
 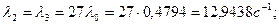
4.
Определение времени цикла замкнутой сети.
Общая формула:  . Определим время цикла для нулевой системы: . Определим время цикла для нулевой системы:
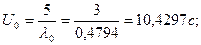
5.
Определение
среднего числа заявок
mi
в каждой СМО.
Общая формула для расчета: 
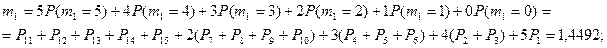
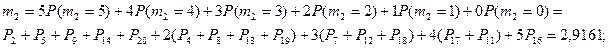

После определения всех характеристик системы для М=1,2,3, необходимо определить быстродействие всех устройств, входящих в модель.
Среднее время обслуживания t1
заявки в СМО, отображающей процессор, определяется параметром t1
=q/QV1
, где V1
– среднее быстродействие процессора, Q – среднее число этапов счета, q - средняя трудоемкость задачи, т.е. среднее число процессорных операций (операций счета). Тогда:

Быстродействия накопителей определим как обратные значениям времени доступа к данным:
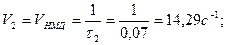
Быстродействие СК определим как средне взвешенную величину от скоростей передачи данных, подключенных к нему накопителей:

где: 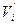 -скорость передачи данных соответствующего накопителя в Кбайт/c. -скорость передачи данных соответствующего накопителя в Кбайт/c.
Найдем стоимость всей СПО, обычно эта величина заранее задается:

где:  - это коэффициент пропорциональности, предполагаем, что - это коэффициент пропорциональности, предполагаем, что  =1; =1;
 -быстродействие i – ого устройства. -быстродействие i – ого устройства.
Тогда: 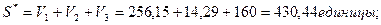
Затем нам требуется при заданной стоимости распределить быстродействия устройств так, чтобы производительность СПО была максимальной.
Для этого определим оптимальные значения быстродействия устройств по формуле:
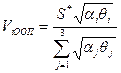 , (2) , (2)
где:  - коэффициент передачи i – ой СМО; - коэффициент передачи i – ой СМО;
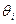 - трудоемкость одного этапа ВП для i – ого устройства, т.е. среднее число операций, которое выполняет i – ое устройство за одно обращение к нему. - трудоемкость одного этапа ВП для i – ого устройства, т.е. среднее число операций, которое выполняет i – ое устройство за одно обращение к нему.
Существует следующее соотношение для 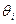 : :

где:  - время обслуживания заявки i -ой СМО. - время обслуживания заявки i -ой СМО.
Тогда: 
 
Найдем отдельно значение знаменателя выражения (2):

В итоге: 
 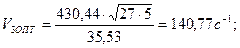
Теперь определим производительность системы 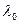 для полученных оптимальных значений быстродействия устройств при М=1: для полученных оптимальных значений быстродействия устройств при М=1:
 
Полученное значение 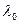 для М=1 оказалось больше значения для М=1 оказалось больше значения 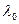 =0,256, рассчитанного выше для того же значения М, что подтверждает тот факт, что оптимально выбранные значения быстродействия устройств обеспечивают максимум производительности. =0,256, рассчитанного выше для того же значения М, что подтверждает тот факт, что оптимально выбранные значения быстродействия устройств обеспечивают максимум производительности.
Для ранее рассчитанных характеристик построим графики их зависимостей от М (числа заявок в системе). 1.
Зависимость коэффициентов загрузки  каждой СМО от М. каждой СМО от М.
2.
Зависимость интенсивности потока входных
заявок  каждой СМО от М. каждой СМО от М.
3.
Зависимость среднего числа заявокм 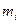 в каждой СМО от М. в каждой СМО от М.
4.
Зависимость времени цикла нулевой системы  от М. от М.
Из построенных зависимостей характеристик модели от М можно сделать следующие выводы:
- узким местом в системе, т.е. устройством, коэффициент загрузки которого стремится к единице при увеличении числа заявок в системе, является накопитель на магнитном диске. Это связано с его быстродействием.
- наибольшую величину интенсивности потока входных заявок имеет процессор, что оправдывает его достаточно высокую стоимость;
- наибольшее среднее число заявок имеет НМД, что говорит о его относительно малом быстродействии;
- время цикла нулевой системы увеличивается с количеством заявок в системе, что реально и должно наблюдаться.
1. Майоров С.А., Новиков Г.И. и др. Основы теории вычислительных систем. М.: 1988
2. Аверцев В.Г. Моделирование систем: Методические указания к курсовому проектированию /Рязан. гос. радиотехн. акад.; 2000, 15 с.
|