|
Исходные данные
Наличие предметов длительного пользования в домашних хозяйствах по регионам Российской Федерации (на 100 домохозяйств , штук)
(Вариант: 6)
| №
|
Области и республики
|
Холодильники. Морозильники
|
Стиральные машины
|
| 1
|
Белгородская
область
|
103
|
93
|
| 2
|
Брянская область
|
99
|
72
|
| 3
|
Владимирская область
|
105
|
90
|
| 4
|
Воронежская область
|
102
|
96
|
| 5
|
Ивановская область
|
106
|
92
|
| 6
|
Калужская область
|
106
|
88
|
| 7
|
Костромская область
|
100
|
85
|
| 8
|
Курская область
|
100
|
78
|
| 9
|
Липецкая область
|
113
|
95
|
| 10
|
Московская область
|
106
|
87
|
| 11
|
Орловская область
|
111
|
93
|
| 12
|
Рязанская область
|
106
|
80
|
| 13
|
Смоленская область
|
115
|
93
|
| 14
|
Тамбовская область
|
108
|
99
|
| 15
|
Тверская область
|
102
|
87
|
| 16
|
Тульская область
|
102
|
93
|
| 17
|
Ярославская область
|
110
|
88
|
| 18
|
Республика Карелия
|
106
|
87
|
| 19
|
Республика Коми
|
111
|
92
|
Задание:
1.Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2.Рассчитайте параметры уравнений линейной, степенной и экспоненциальной парной регрессии.
3.Оцените тесноту связи с помощью показателей корреляции и детерминации.
4.Дайте с помощью среднего (общего) коэффициента эластичности сравнительную характеристику силы связи фактора с результатом.
5.Оцените качество уравнений с помощью средней ошибки аппроксимации.
6.Оцените статистическую надёжность результатов регрессионного моделирования с помощью F-критерия Фишера. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование
7.Рассчитайте ожидаемое значение результата, если значение фактора увеличится на 5% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости α=0,05.
Задание №1.
Постройте поле корреляции и сформулируйте гипотезу о форме связи.

Задание №2.
Рассчитайте параметры уравнений линейной, степенной и экспоненциальной парной регрессии.
| №
|
х
|
у
|
ху
|
х²
|
у²
|
lnx
|
lny
|
| 1
|
103
|
93
|
9579
|
10609
|
8649
|
2
|
2
|
| 2
|
99
|
72
|
7128
|
9801
|
5184
|
2
|
1,9
|
| 3
|
105
|
90
|
9450
|
11025
|
8100
|
2
|
2
|
| 4
|
102
|
96
|
9792
|
10404
|
9216
|
2
|
2
|
| 5
|
106
|
92
|
9752
|
11236
|
8464
|
2
|
2
|
| 6
|
106
|
88
|
9328
|
11236
|
7744
|
2
|
1,9
|
| 7
|
100
|
85
|
8500
|
10000
|
7225
|
2
|
1,9
|
| 8
|
100
|
78
|
7800
|
10000
|
6084
|
2
|
1,9
|
| 9
|
113
|
95
|
10735
|
12769
|
9025
|
2,1
|
2
|
| 10
|
106
|
87
|
9222
|
11236
|
7569
|
2
|
1,9
|
| 11
|
111
|
93
|
10323
|
12321
|
8649
|
2
|
2
|
| 12
|
106
|
80
|
8480
|
11236
|
6400
|
2
|
1,9
|
| 13
|
115
|
93
|
10695
|
13225
|
8649
|
2,1
|
2
|
| 14
|
108
|
99
|
10692
|
11664
|
9801
|
2
|
2
|
| 15
|
102
|
87
|
8874
|
10404
|
7569
|
2
|
1,9
|
| 16
|
102
|
93
|
9486
|
10404
|
8649
|
2
|
2
|
| 17
|
110
|
88
|
9680
|
12100
|
7744
|
2
|
1,9
|
| 18
|
106
|
87
|
9222
|
11236
|
7569
|
2
|
1,9
|
| 19
|
111
|
92
|
10212
|
12321
|
8464
|
2
|
2
|
| ∑
|
2011
|
1688
|
178950
|
213227
|
150754
|
38
|
37
|
| x¯
|
105,8
|
|
|
|
|
|
|
| y¯
|
88,8
|
|
|
|
|
|
|
| x¯y
|
9418,4
|
|
|
|
|
|
|
Линейная парная регрессия:




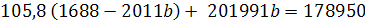
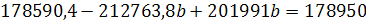
-10772,8b = 359,6
B = 0,03
2011a + 201991*0,03 = 178950
2011a + 6059,7 = 178950
2011a = 178952 – 6059,7
2011a = 172890,3
A = 86

Степенная парная регрессия:
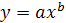

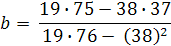
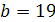
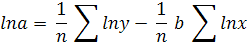
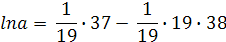
a = 1,56

Экспоненциальная парная регрессия:


Задание №3.
| №
|
х
|
у
|
ху
|
х²
|
у²
|
у^
|
у - у¯
|
| 1
|
103
|
93
|
9579
|
10609
|
8649
|
89,1
|
3,9
|
| 2
|
99
|
72
|
7128
|
9801
|
5184
|
89
|
-17
|
| 3
|
105
|
90
|
9450
|
11025
|
8100
|
89,2
|
0,8
|
| 4
|
102
|
96
|
9792
|
10404
|
9216
|
89,1
|
6,9
|
| 5
|
106
|
92
|
9752
|
11236
|
8464
|
89,2
|
2,8
|
| 6
|
106
|
88
|
9328
|
11236
|
7744
|
89,2
|
-1,2
|
| 7
|
100
|
85
|
8500
|
10000
|
7225
|
89
|
-4
|
| 8
|
100
|
78
|
7800
|
10000
|
6084
|
89
|
-11
|
| 9
|
113
|
95
|
10735
|
12769
|
9025
|
89,4
|
5,6
|
| 10
|
106
|
87
|
9222
|
11236
|
7569
|
89,2
|
-2,2
|
| 11
|
111
|
93
|
10323
|
12321
|
8649
|
89,3
|
3,7
|
| 12
|
106
|
80
|
8480
|
11236
|
6400
|
89,2
|
-9,2
|
| 13
|
115
|
93
|
10695
|
13225
|
8649
|
89,5
|
3,5
|
| 14
|
108
|
99
|
10692
|
11664
|
9801
|
89,2
|
9,8
|
| 15
|
102
|
87
|
8874
|
10404
|
7569
|
89,1
|
-2,1
|
| 16
|
102
|
93
|
9486
|
10404
|
8649
|
89,1
|
3,9
|
| 17
|
110
|
88
|
9680
|
12100
|
7744
|
89,3
|
-1,3
|
| 18
|
106
|
87
|
9222
|
11236
|
7569
|
89,2
|
-2,2
|
| 19
|
111
|
92
|
10212
|
12321
|
8464
|
89,3
|
2,7
|
| ∑
|
2011
|
1688
|
178950
|
213227
|
150754
|
1694,6
|
-6,6
|
| x¯
|
105,8
|
|
|
|
|
|
|
| y¯
|
88,8
|
|
|
|
|
|
|
| x¯y
|
9418,4
|
|
|
|
|
|
|

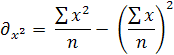


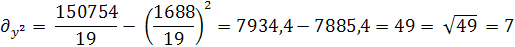





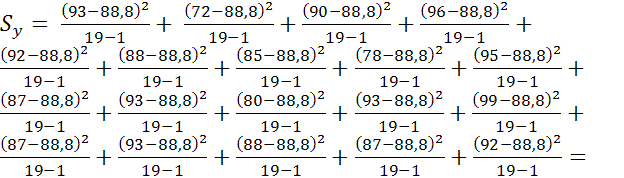 43,82 43,82
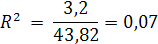
Задание №4.
Линейная парная регрессия:
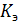 = = 

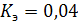
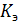 
Степенная парная регрессия:


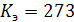
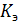 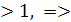
Экспоненциальная парная регрессия:
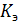 = = 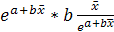




|