Санкт-Петербургский Государственный Университет Телекоммуникаций им. проф. М.А. Бонч-Бруевича
Кафедра ПРЭС
Курсовой проект по дисциплине
“Прикладная механика”
Работу выполнил:
Ст. Гр. ТСС-71
Игорев А.Н.
Руководитель проекта:
Чуракова Л.Д.
Санкт-Петербург
2009
Содержание:
1. Определение равнодействующей плоской системы сил
2. Определение центра тяжести фигуры
3. Расчёт на прочность элемента конструкции РЭА
4. Расчет задачи
Список литературы
1. Определение равнодействующей плоской системы сил
Вариант № 15
Условие задачи:
Блок радиоаппаратуры находится под действием системы 3 сил, заданных модулями 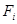 сил, величинами углов сил, величинами углов 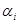 , составленных силами с положительной осью X, и координатами , составленных силами с положительной осью X, и координатами 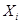 и и 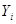 точек приложения сил. Требуется определить равнодействующую силу. Исходные значения указаны в таблице 1. точек приложения сил. Требуется определить равнодействующую силу. Исходные значения указаны в таблице 1.
Таблица 1.
Значение сил, углов и координат.
| Силы, Н
|
Углы, град
|
Координаты, см
|
| 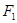
|
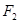
|
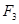
|
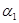
|
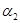
|
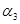
|
x1/ y1
|
x2/ y2
|
x3/ y3
|
| 75
|
85
|
110
|
165
|
120
|
240
|
45/ –35
|
15/ 45
|
–35/ 15
|
Решение:
1)Определение главного вектора аналитически
Fx = F * cosα;
Fy = F * sinα;
cos 165= cos (120 + 45)= cos120 * cos45 – sin120 * sin45 = – 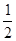 * * – – 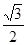 * * = –0,97; = –0,97;
cos120 = – 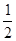 = – 0,5; = – 0,5;
cos 240 = – 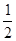 = – 0,5; = – 0,5;
sin 165 = sin (120 + 45) = sin120 * cos45 + cos120* sin45 = 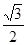 * *  – – 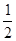 * * = 0,26; = 0,26;
sin 120 = 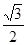 = 0,87; = 0,87;
sin 240 = – 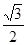 = – 0,87. = – 0,87.
Определяем проекции сил 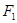 , , 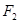 , , 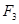 на координатные оси X,Y: на координатные оси X,Y:
F1x = F1 * cos165 = 75 * (– 0,97) = – 72,75 Н;
F1y = F1 * sin165 = 75 * 0,26 = 19,5 Н;
F2x = F2 * cos120= 85 * (– 0,5) = – 42,5 Н; (1)
F2y = F2 * sin120 = 85 * 0,87 = 73,95 Н;
F3x = F3 * cos240 = 110 * (– 0,5) = – 55 Н;
F3y = F3 * sin240 = 110 * (– 0,87) = – 95,7 Н;
Определяем проекции главного вектора системы на оси координат:
Rx =Σ Fix = – 72,75 – 42,5 – 55 = –170,25 ; (2)
Ry =Σ Fiy = 19,5 + 73,95 – 95,7 = – 2,25 ;
Расчёты по формулам (1) и (2) приводятся в таблице 2, в которой также определили главный момент системы:
Таблица 2.
| Номер силы, i
|
Значение
силы
Fi, Н
|
Угол направления
силы, град
|
Координаты, м
|
Проекции
сил, Н
|
Проекции
сил, Н
|
Произведения величин, Н/м
|
Главный момент системы Mo,Н/м
|
| Xi
|
Yi
|
Fix
|
Fiy
|
Xi*Fiy
|
Yi*Fix
|
–––
|
| 1
|
75
|
165
|
0,45
|
–0,35
|
–72,75
|
19,5
|
8,775
|
25,46
|
–––
|
| 2
|
85
|
120
|
0,15
|
0,45
|
– 42,5
|
73,95
|
11,025
|
–19,13
|
–––
|
| 3
|
110
|
240
|
–0,35
|
0,15
|
– 55
|
– 95,7
|
33,495
|
– 8,25
|
–––
|
| Суммарное значение параметра
|
–170,25
|
– 2,25
|
53,3
|
– 1,9
|
168
|
Определяем главный вектор системы:
 H H
Где значения  и и 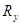 принимают из таблицы. Направление главного вектора определяет угол принимают из таблицы. Направление главного вектора определяет угол 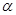 , который определяем из формул: , который определяем из формул:
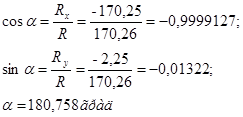
Определение главного момента системы сил относительно начала координат:
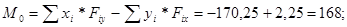
2)Определение главного вектора системы сил графически.
Построение выполнили на листе формата А3. Масштабы длин и сил выбраны так, чтобы максимально использовать площадь листа. Определим масштабные значения величин:
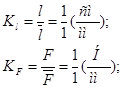
где l , F –действительное значение длины и силы соответственно,
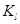 -масштабный коэффициент длин, -масштабный коэффициент длин,
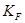 - масштабный коэффициент сил. - масштабный коэффициент сил.
Учитывая заданные значения координат, наносят на чертеже координатные оси, точки приложения сил 1,2,3, и изображаем сами силы.
Определяем действительное значение главного вектора

Где масштабное значение  мм, принимают по чертежу. мм, принимают по чертежу.
Направление вектора  определяем по чертежу: определяем по чертежу:
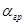 =181 градус. =181 градус.
3)Относительные отклонения определения параметров графическим способом.
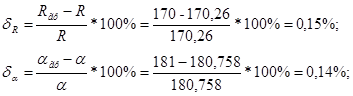
Отклонения не превышают 2-3% , следовательно, построения и расчёты выполнены правильно.
4)Определение значения и положения равнодействующей.
Определяем плечо пары сил:

Где С - точка приложения равнодействующей.
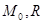 - действительные значения главного момента и главного вектора, определённые аналитически. - действительные значения главного момента и главного вектора, определённые аналитически.
2. Определение центра тяжести фигуры
Условия:
Определить координаты центра тяжести (центра масс) шасси блока РЭА. Шасси изготовлено из листового материала и представляет собой сложную фигуру.
a=280 мм; b=140 мм; c=65мм.
Решение:
При аналитическом определении положения центра тяжести (центра масс) исходят из понятия “центр параллельных сил”. Полагая, что материал тела сплошной и однородный, приведём формулы для определения координат центра тяжести (центра масс) сложной фигуры:
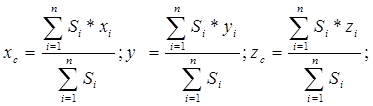
Где 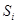 - площадь i–ой части сложной фигуры. - площадь i–ой части сложной фигуры.
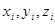 –координаты центра тяжести i–ой части фигуры. –координаты центра тяжести i–ой части фигуры.
n – число частей сложной фигуры.
Вычисление координат центра тяжести (центра масс) простых фигур составляющих сложную:
1)
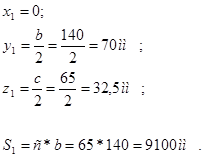
2)
 
3)

4)
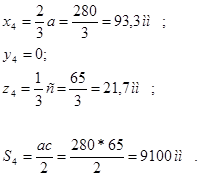
Вычисление координат центра тяжести (центра масс) сложной фигуры:
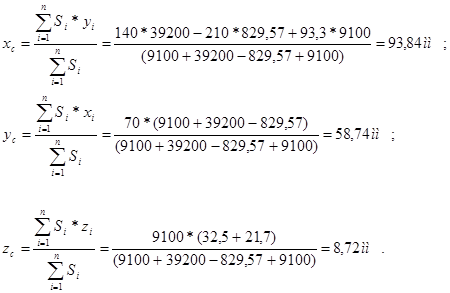
Координаты центра тяжести фигуры [93,84; 58,74; 8,72] мм (относительно начала координат).
3. Расчёт на прочность элемента конструкции РЭА
Условия:
Построить эпюры продольных сил. Определить размеры прямоугольного и круглого поперечного сечения стержня, растянутого силой. Определить абсолютное удлинение стержня. Материал стержня сталь 20 нормализированная. Определить опасное сечение стержня. F=2000 Н; l=140 мм, отношение b/a = 2.

Решение:
1)Из уравнения равновесия определяем реакцию заделки:
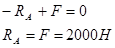
2) Построение эпюр продольных сил:
участок 0≤ X ≤ l, идём слева
 ; ;
3) Определение допускаемого напряжения:
Допускаемое напряжение можно определить по формуле:
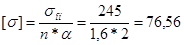 МПа; МПа;
Где  - опасное напряжение, - опасное напряжение,
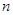 - коэффициент запаса прочности принимают в пределах 1,5-2 - коэффициент запаса прочности принимают в пределах 1,5-2
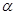 - коэффициент концентрации напряжения принимают в пределах 1,5-,2,5 - коэффициент концентрации напряжения принимают в пределах 1,5-,2,5
В качестве опасного напряжения  для металлов обычно принимают предел текучести для металлов обычно принимают предел текучести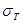 , который принимают по таблице 5. , который принимают по таблице 5.
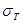 =245 МПа (материал – сталь 20) =245 МПа (материал – сталь 20)
4) Построение эпюр нормальных напряжений:
Из условия прочности можно определить площадь поперечного сечения:
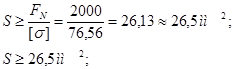
а) Если сечение - прямоугольник:
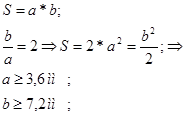
б) Если сечение – круг:
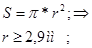
Т.е. высота должна быть a≥ 3,6 мм, ширина b должна быть b≥ 7,2 мм.
Если сечение круглое, тогда r≥ 2,9 мм
участок 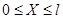 , идём слева , идём слева
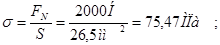
5) Расчет на прочность:
Условие прочности при растяжении сжатии

Т.к. допускаемое напряжение больше действующего в опасном сечении то после снятия напряжения конструкции вернется в исходное состояние (не останется остаточной деформации.)
6) Расчёт удлинения стержня:
При расчёте жёсткости стержня определяют его абсолютное удлинение (укорочение) по формуле
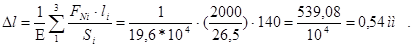 ; ;
где i-номер участка
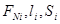 - соответственно продольная сила на участке, длина участка, площадь поперечного сечения на участке. - соответственно продольная сила на участке, длина участка, площадь поперечного сечения на участке.
4.
Расчётно-графическая работа
Условие задачи:

Манипулятор промышленного робота типа 2В состоит из двух вращающихся звеньев 1 и 2. Звенья движутся в плоскости XOY. Центр схвата манипулятора – точка С. Заданы функции изменения углов 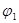 и и  ( (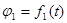 , , 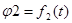 ) и размеры звеньев ) и размеры звеньев 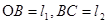 . Определить скорости и ускорения центра схвата и звеньев манипулятора при движении робота в течении t с (значения определить через каждые . Определить скорости и ускорения центра схвата и звеньев манипулятора при движении робота в течении t с (значения определить через каждые 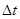 с). По результатам расчёта построить графики зависимостей скоростей и ускорений центра и звеньев манипулятора. Проанализировать полученные графики. с). По результатам расчёта построить графики зависимостей скоростей и ускорений центра и звеньев манипулятора. Проанализировать полученные графики.
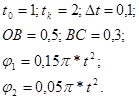
Решение:
1.1 Задаём движение подвижным звеньям манипулятора:
Звенья совершают вращательные движения, закон движения имеет вид

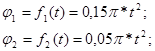 (1) (1)
где 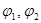 - углы поворота звеньев вокруг центра шарнира сочленяющего данные звенья с предыдущими звеньями кинематической схемы. - углы поворота звеньев вокруг центра шарнира сочленяющего данные звенья с предыдущими звеньями кинематической схемы.
t - время.
1.2 Исследуем движения звеньев манипулятора:
Дифференцируя уравнения типа (1), определяем угловую скорость и угловое ускорение:

(2)
(3)
Используя формулы (2),(3) определяем скорости и ускорения звеньев для моментов времени 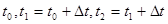 и так далее. Результаты расчётов представлены в Таблице №1. и так далее. Результаты расчётов представлены в Таблице №1.
Таблица №1
Значения скоростей и ускорения звеньев
| Моменты времени, с
|
Звено 1
|
Звено 2
|
| 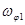 , 1/с , 1/с
|
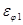 , 1/c2 , 1/c2
|
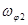 , 1/с , 1/с
|
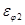 , 1/c2 , 1/c2
|
| 1
|
0,940
|
0,94
|
0,310
|
0,31
|
| 1,1
|
1,034
|
0,94
|
0,341
|
0,31
|
| 1,2
|
1,128
|
0,94
|
0,372
|
0,31
|
| 1,3
|
1,222
|
0,94
|
0,403
|
0,31
|
| 1,4
|
1,316
|
0,94
|
0,434
|
0,31
|
| 1,5
|
1,410
|
0,94
|
0,465
|
0,31
|
| 1,6
|
1,504
|
0,94
|
0,496
|
0,31
|
| 1,7
|
1,598
|
0,94
|
0,527
|
0,31
|
| 1,8
|
1,692
|
0,94
|
0,558
|
0,31
|
| 1,9
|
1,786
|
0,94
|
0,589
|
0,31
|
| 2
|
1,880
|
0,94
|
0,620
|
0,31
|
Строим графики зависимости параметров 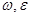 от времени t для двух звеньев. от времени t для двух звеньев.
Анализ графиков:
1.3.Определение движения центра схвата:
Используя формулы (1), определяющие движения отдельных звеньев, заданные размеры звеньев, записываем уравнения движения центра схвата в координатной форме
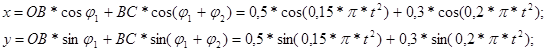 (4) (4)
Уравнения (4) определяют положение исследуемой материальной точки в любой момент времени t. Дифференцируя уравнения (4) , определяем проекции скорости точки на координатные оси:
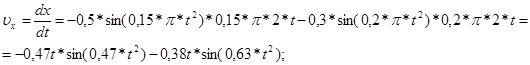 (5) (5)
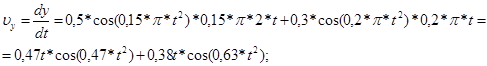
Дифференцируя полученные значения скоростей, получаем проекции ускорения точки:
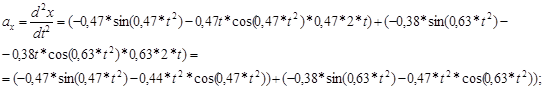 (6) (6)
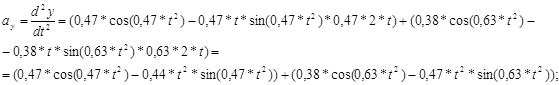
Скорость и ускорение точки по модулю определяются в виде:
 (7) (7)
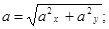 (8) (8)
1.4 Исследование движения центра схвата:
По формулам (5) и (6) определяем значения проекций скорости и ускорения исследуемой точки на оси координат для моментов времени 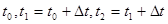 и так далее. По формулам (7) и (8) определяют скорость и ускорение точки для тех же моментов времени. Результаты расчётов представляют в Таблице 2. и так далее. По формулам (7) и (8) определяют скорость и ускорение точки для тех же моментов времени. Результаты расчётов представляют в Таблице 2.
Таблица 2:
| Моменты времени, 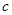
|
Проекции ускорения, 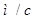
|
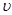 , ,
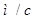
|
Проекции ускорения,

|
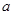 , ,
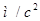
|
| 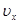
|
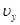
|
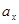
|
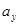
|
| 1
|
-0,0080336
|
0,84996121
|
0,84999919
|
-0,9179904
|
0,84118409
|
1,24510925
|
| 1,1
|
-0,0106926
|
0,93493753
|
0,93499834
|
-1,1107440
|
0,83709273
|
1,39084938
|
| 1,2
|
-0,0138818
|
1,01990349
|
1,01999794
|
-1,3218391
|
0,83171967
|
1,56173500
|
| 1,3
|
-0,0176493
|
1,10485599
|
1,10499694
|
-1,5512678
|
0,82482167
|
1,75691848
|
| 1,4
|
-0,0220432
|
1,18979141
|
1,18999558
|
-1,7990198
|
0,81613441
|
1,97548667
|
| 1,5
|
-0,0271117
|
1,27470549
|
1,27499376
|
-2,0650822
|
0,80537248
|
2,21657152
|
| 1,6
|
-0,0329028
|
1,35959333
|
1,35998085
|
-2,3494392
|
0,79222938
|
2,47941362
|
| 1,7
|
-0,0394645
|
1,44444935
|
1,44498835
|
-2,6520714
|
0,77637761
|
2,76337563
|
| 1,8
|
-0,0468450
|
1,52926720
|
1,52998451
|
-2,9729552
|
0,75746865
|
3,06793438
|
| 1,9
|
-0,0550921
|
1,61403975
|
1,61497915
|
-3,3120629
|
0,73513302
|
3,39266579
|
| 2
|
-0,0642536
|
1,69875905
|
1,69997375
|
-3,6693614
|
0,70898037
|
3,73759635
|
Таблица 3:
Координаты движения центра схвата.
| Моменты времени, 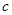
|
Значения координат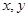 м. м.
|
| 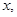 м. м.
|
 м. м.
|
| 1
|
0,79996505
|
0,00740209
|
| 1,1
|
0,79994883
|
0,00895646
|
| 1,2
|
0,79992752
|
0,01065883
|
| 1,3
|
0,79990018
|
0,01250918
|
| 1,4
|
0,79998657
|
0,01450747
|
| 1,5
|
0,79982307
|
0,01665367
|
| 1,6
|
0,79977096
|
0,01894775
|
| 1,7
|
0,79970811
|
0,02138965
|
| 1,8
|
0,79963313
|
0,02397931
|
| 1,9
|
0,79954455
|
0,02671667
|
| 2
|
0,79944087
|
0,02960162
|
По данным табл.2 строят графики зависимости параметров  от времени t. По данным табл.3 строят график перемещения центра схвата. от времени t. По данным табл.3 строят график перемещения центра схвата.
Оценка графиков:
Зависимости V и a от t (1 ,0<t<2,0):
Из анализа графиков скорости и ускорения видно, что cкорость и ускорение в промежутке времени от t0 до tk возрастают, поэтому движении ускоренное.
Траектории движения центра схвата (1 ,0<t<2,0):
Из анализа графика видно, что центр схвата манипулятора перемещается в плоскости XOY по прямой вдоль линии OY.
Список литературы:
1) Методические указания к выполнению расчетно-графических работ 1 и 2 по теоретической механике. С.С. Степанов, Л.Д. Чуракова; ЛЭИС. – Л., 2009г.
2) Методические указания к лабораторным работам по курсу ”Прикладная механика”. В.Ф. Рожченко, С.С. Степанов, Л.Д. Чуракова; ЛЭИС. – Л., 2009г.
3) Курс лекций по курсу прикладная механика. Л.Д. Чуракова.
|