| Глава
I
. Подбор двигателя и предварительный кинематический расчёт
§1. Определение ориентировочного к.п.д. редуктора
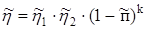 , ,
где по [1]*
,[2], 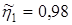 - примерный к.п.д. быстроходной зубчатой - примерный к.п.д. быстроходной зубчатой
пары повышенной степени точности;
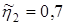 - примерный к.п.д. червячной передачи с - примерный к.п.д. червячной передачи с
однозаходным цилиндрическим червяком
(z
ч
=1 с целью малогабаритности);
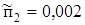 - примерный коэффициент потерь на валу - примерный коэффициент потерь на валу
с подшипниками качения;
 – число последовательных валов.
– число последовательных валов.
Численно
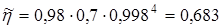
§2. Определение потребной мощности электродвигателя
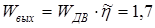 кВт. кВт.
Выбираем электродвигатель типа МПЩ мощностью 2,2 кВт с n
= 5000
об/мин.
§3. Определение диаметра звездочки (рис.3)
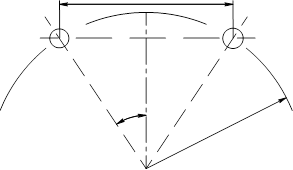
Рис.1. Теоретические размеры цепной звездочки.
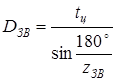 , ,
где по исходным данным
 мм – шаг цепи; мм – шаг цепи;
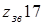 – число зубьев звездочки – число зубьев звездочки
Численно
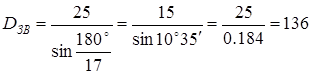 мм. мм.
§4. Расчет числа оборотов в минуту звездочки (выходного вала редуктора)
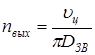 об/мин, об/мин,
где υ
ц
=8,0 м/мин
– скорость движения цепи (по исходным данным);
D
ЗВ
=0,136 м
(§4).
Численно
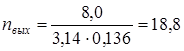 об/мин. об/мин.
§5. Общее передаточное число редуктора
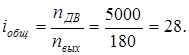
§6. Разбивка передаточного числа по передачам механизма
1. Определяем максимально допустимое передаточное число данного механизма по максимально допустимым передаточным числам его передач:
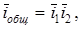
где 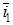 =6 – максимальное передаточное число конической передачи =6 – максимальное передаточное число конической передачи
([1],[2],[3]);
 ≈80 - максимальное передаточное число червячной передачи с ≈80 - максимальное передаточное число червячной передачи с
однозаходным червяком.
Численно
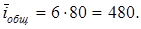
2. Определяем делитель для разбивки передаточного числа по передачам
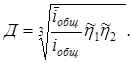
П р и м е ч а н и е. Показатель корня равен числу последовательно работающих передач механизма.
Численно
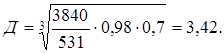
3. Разбивка передаточного числа по передачам производим по формуле

где индекс i
– номер передачи по ходу движения.
Итак,
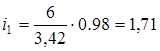 ; ;
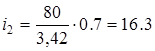 . .
Так как в червячной передаче взято z
ч
=1 то 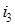 должно быть целым числом. должно быть целым числом.
Поэтому принимаем
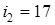 . .
Тогда
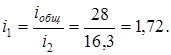
Глава
II
. Расчет червячной передачи
Схема червячной передачи помещена на рисунке.
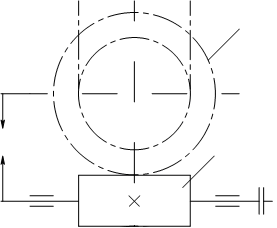 Рисунок – 2 Кинематическая схема червячной передачи редуктора.
Исходные данные
1. Число оборотов ведущего вала n
1
=180 (n
н
в предыдущем расчете).
2. Передаточное число i
= 17 (i
3
в разд. I, §7, п. 3).
3. Коэффициент возможной неравномерности раздачи усилий на две цепи К
нер
=1,25.
4. Коэффициент динамичности внешней нагрузки на валах червячных колес K
д
=1,05.
5. Ориентировочный к. п. д. 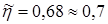 . .
§ 1. Определение угловых скоростей
Для червяка
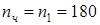 об/мин; об/мин;
Для колеса
 об/мин. об/мин.
§ 2. Определение крутящих моментов
На червяке:
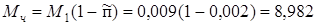 кГмм = кГмм =  Нмм, Нмм,
где 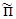 ≈0,002 – примерное значение коэффициента потерь вала на ≈0,002 – примерное значение коэффициента потерь вала на
подшипниках качения;
на червячном колесе (предварительно)
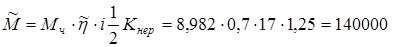 кГмм = кГмм = 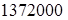 Нмм (далее подлежит уточнению). Нмм (далее подлежит уточнению).
§ 3. Выбор материалов червяка и червячного венца [
I
]
1. Червяк изготовлен из стали 40ХНА, имеет удовлетворительную вязкость и повышенную прочность после закалки с высоким отпуском:
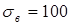 кГ/мм
2
; кГ/мм
2
; 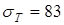 кГ/мм
2
; кГ/мм
2
;  кГ/мм
2
; кГ/мм
2
; 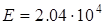 кГ/мм
2
. кГ/мм
2
.
НВ = 280ч310 (ввиду кратковременности работы высокая твердость здесь не обязательна).
2.Венец червячного колеса при ожидаемой скорости скольжения υ
ск
<5 м/сек
изготовлен из бронзы марки БрАЖ-9-4 (литье в киль) со следующими механическими характеристиками:
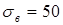 кГ/мм2
; кГ/мм2
;  кГ/мм2
; кГ/мм2
; 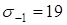 кГ/мм
2
; кГ/мм
2
; 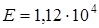 кГ/мм
2
. кГ/мм
2
.
§ 4. Определение числа циклов изменения напряжений
зубьев червячного
колеса за расчетную долговечность.
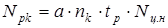 ,
,
где a
=1,
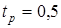 мин мин
Согласно расчету в 1-й ступени редуктора величина  оказалась практически одинаковой для контактных и изгибных напряжений зубьев. оказалась практически одинаковой для контактных и изгибных напряжений зубьев.
1. По контактным напряжениям:
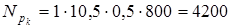 циклов. циклов.
2. По изгибным напряжениям.
Проверку нужно провести дважды: при r
=0 и  циклов
и при r
=-0,5 (реверс момента) соответственно числу реверсов циклов
и при r
=-0,5 (реверс момента) соответственно числу реверсов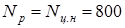 циклов. циклов.
§ 5. Определение допускаемых контактных напряжений для зубьев червячного колеса
Здесь их величины ограничиваются сверху и снизу так же, как и на рис.5, но по другим формулам [I], выраженным через  . .
Для безоловянистых бронз
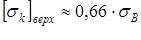 кГ/мм2
= кГ/мм2
= 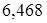 Н/мм2
; Н/мм2
;
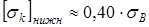 кГ/мм2
= кГ/мм2
= Н/мм2
. Н/мм2
.
Из записи условия
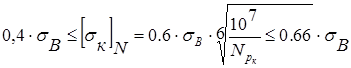 , ,
т. е. в числах
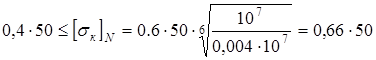 , ,
получается
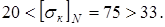
Следовательно, нужно принять для расчета
 кГ/мм
2
= кГ/мм
2
= Н/мм2
. Н/мм2
.
§ 6. Предварительный выбор
степени
точности червячного
зацепления
Ввиду небольшой величины ожидаемой окружной червячного колеса принимаем 8-ю степень точности.
§ 7. Выбор исходных параметров червячной пары
1. Число заходов резьбы червяка
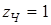
(выбрано ранее с целью уменьшения габаритности червячной ступени).
2. Число зубьев червячного колеса
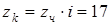
3. Число осевых модулей в делительном диаметре червяка
q
= 8
4. Угловая ширина червячного венца
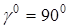
5. Угол подъема винтовой линии по делительному диаметру червяка
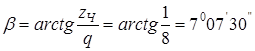
§ 8. Поправочные коэффициенты, определяющие расчетную величину погонной нагрузки
1. Коэффициент концентрации погонной нагрузки по длине червячного зуба
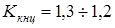 . .
При малой длительности работы принимаем  (приработка за счет износа не успевает проявиться). (приработка за счет износа не успевает проявиться).
2. Скоростной коэффициент.
Ввиду весьма небольшой ожидаемой величины  м/сек
можно принять в первом приближении м/сек
можно принять в первом приближении
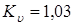
3. Коэффициент профильного перекрытия зубьев.
При расчете по контактным напряжениям при 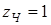 независимо от степени точности независимо от степени точности 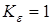 . .
§ 9. Определение межосевого расстояния из расчета
на контактную
прочность червячных зубьев на
номинальном режиме (первое
приближение)
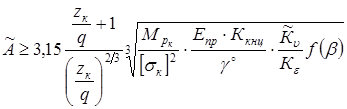 мм
, мм
,
где:
1) расчетный момент на колесе
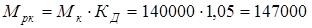 кГ/мм =
кГ/мм = Н/мм. Н/мм.
) приведенный модуль упругости
 кГ/мм2
= кГ/мм2
= 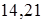 Н/мм2
; Н/мм2
;
3) величина, учитывающая влияние на контактные напряжения наклона
червячных зубьев под углом 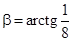 (§7, п. 5), (§7, п. 5),
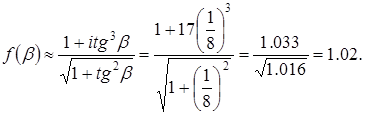
Подставляя численные значения, получаем
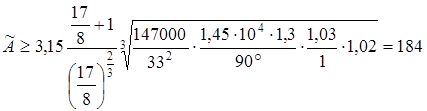 мм. мм.
Ввиду большой близости коэффициента K
υ
к единице второго приближения можно не выполнять, поскольку уточненное значение 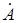 будет пренебрежимо отличаться от будет пренебрежимо отличаться от 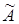 ( (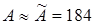 мм). мм).
§ 10. Подбор осевого модуля червяка и зубьев червячного колеса
По геометрической формуле находим
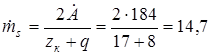 мм. мм.
По ГОСТу 2144-66 принимаем 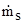 = 15 мм (в большую сторону). = 15 мм (в большую сторону).
§ 11. Определение основных размеров червячной пары
1. Точное значение межосевого расстояния (до 0,01 мм)
 мм. мм.
2. Точные значения делительных диаметров червяка и колеса:
 мм; мм;
 мм. мм.
3. Рабочая дуговая ширина червячного венца
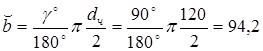 мм. мм.
4. Угол зацепления в осевой плоскости червяка
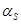 =200
; =200
; 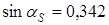 ; ; 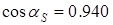 . .
5. Длина резьбовой части червяка [I].
При 
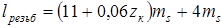 мм, мм,
где последнее слагаемое — технологическая прибавка для шлифуемых
червяков.
Численно:
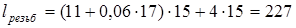 мм. мм.
§ 12. Проверка выбора степени точности зацепления и уточнение скоростного коэффициента
1. Фактическая окружная скорость червячного колеса
 м/сек. м/сек.
2. Предельно допустимое значение окружной скорости для бронзовых
червячных колес с цилиндрическим червяком при 8-й степени точности,
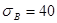 кГ/мм2
и при кГ/мм2
и при 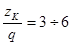
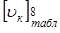 =2 =2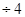 соответственно значению соответственно значению  [I]. [I].
Интерполируя по линейному закону для 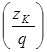 = =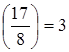 (рис. 13), (рис. 13),
получаем
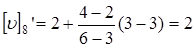 м/сек. м/сек.
С поправкой на 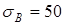 кГ/мм2
=
490 Н/мм2
,
находим кГ/мм2
=
490 Н/мм2
,
находим
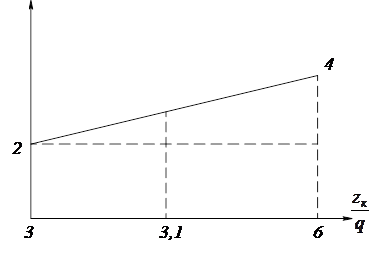 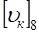 =2× =2×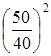 = 3,1 м/сек. = 3,1 м/сек.
Рисунок – 3.
3. Правильность выбора степени точности проверяем по условию
(1,5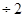 ) )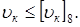
При среднем значении (1,75) коэффициента запаса на нераскрытие контактов зубьев получаем 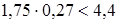 , т.е , т.е  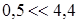 м/сек. м/сек.
Оставляем 8-ю степень точности, поскольку более грубые степени точности в механизмах летательных аппаратов не применяются
4. Скоростной коэффициент
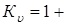 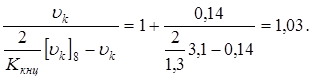
§ 13. Уточнение к. п. д. червячной пары
1. Приведенный коэффициент трения червячных зубьев в паре бронза — сталь при правильно подобранной смазке
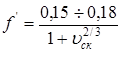 , ,
где 0,15 — при шлифованной резьбе червяка и 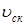 — скорость скольжения — скорость скольжения
вдоль по винтовой линии:
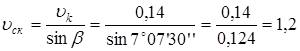 м/сек; м/сек;
 . .
Приведённый угол трения 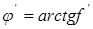 , т.е. , т.е. 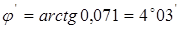 . .
2. К. п. д. червячной пары

При шлифованной резьбе находим
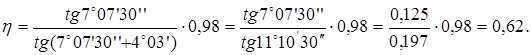
§ 14.Уточнение крутящего момента на червячном колесе в связи с уточнением к. п. д.
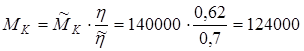 кГмм =
кГмм = 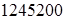 Нмм. Нмм.
§ 15. Проверка полученных размеров червячной пары на контактную прочность зубьев
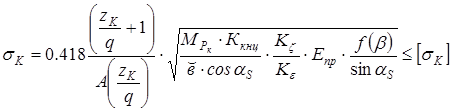 кГ/мм2
, кГ/мм2
,
где 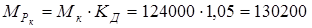 кГмм= кГмм=  Н/мм. Н/мм.
Подставляя принятые и найденные входящие сюда величины, получаем:
1. На номинальном режиме
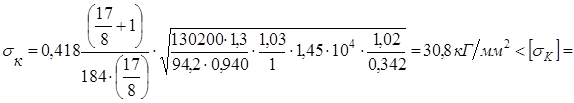 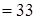 кГ/мм2
= кГ/мм2
= 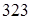 Н/мм2
. Н/мм2
.
2. На перегрузочном режиме пробуксовки муфты с коэффициентом перегрузки 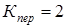 . .
 кГ/мм2
= кГ/мм2
= 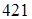 Н/мм2
, Н/мм2
,
что превышает
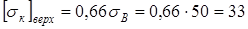 кГ/мм2
= кГ/мм2
=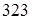 Н/мм2
. Н/мм2
.
Это легко можно исправить, перейдя на более прочную бронзу с включением никеля БрАЖН-4-4 (литье в кокиль, 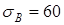 кГ/мм
2
) и пойдя на уширение червячного венца. кГ/мм
2
) и пойдя на уширение червячного венца.
Тогда новое значение
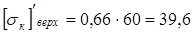 кГ/мм2
= кГ/мм2
=  Н/мм2
; Н/мм2
;
новое значение угловой ширины
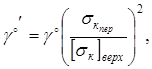 т.е. т.е.
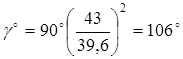 . .
3. На номинальном режиме
 кГ/мм2
< кГ/мм2
<
=33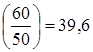 кГ/мм2
= кГ/мм2
= Н/мм2
, Н/мм2
,
на перегрузочном режиме
 кГ/мм2
= кГ/мм2
= 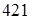 Н/мм2
= Н/мм2
= . .
В результате принимаем новое значение угловой ширины червячного венца 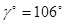 и дуговой ширины и дуговой ширины
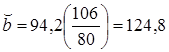 мм. мм.
§ 16. Определение расчетных изгибных напряжений в зубьях червячного колеса (на номинальном режиме)
1. Эквивалентное число зубьев для червячного колеса
 . .
2. Коэффициент формы профиля зуба
 . .
3. Расчетное напряжение изгиба
 ,
,
где
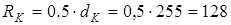 мм;
мм;
 мм; мм;
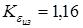 - коэффициент профильного перекрытия червячных зубьев 8-й - коэффициент профильного перекрытия червячных зубьев 8-й
степени точности при расчете на изгиб [I].
Численно
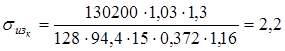 кГ/мм2
=
кГ/мм2
=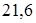 Н/мм2
. Н/мм2
.
§ 17. Допускаемые напряжения зубьев червячного колеса на изгиб
1. Механические характеристики бронзы БрАЖН-10-4-4 (литье в кокиль):
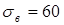 кГ/мм2
; кГ/мм2
; 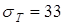 кГ/мм2
; кГ/мм2
; 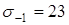 кГ/мм2
. кГ/мм2
.
2.
Теоретический коэффициент концентрации напряжений у корня зуба
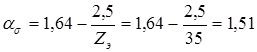 . .
3. Коэффициент чувствительности литой бронзы к концентрации
напряжений
q
= 0,4.
4. Эффективный коэффициент концентрации напряжений у корня зуба
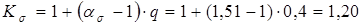 . .
5. Коэффициент влияния чистоты поверхности у корня зуба
 , ,
где a
=6 после чистового нарезания 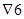 червячных зубьев. червячных зубьев.
Численно
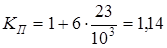 . .
6. Коэффициент качества литой заготовки (литье в кокиль) [I]
 . .
7. Масштабные коэффициенты зуба [I].
Соответственно 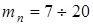 мм принимают мм принимают 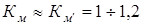 . .
При 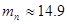 мм мм

8.Результирующие коэффициенты влияния отличий детали от экспериментального образца материала:
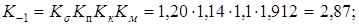
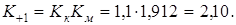
9. Предел ограниченной выносливости материала зубьев
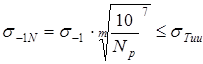 , ,
где 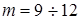 ; ;  - по §4, п. 2; - по §4, п. 2; 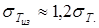 
При  , ,
 кГ/мм2
,> кГ/мм2
,> 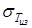 = =
=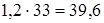 кГ/мм2
= кГ/мм2
=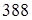 Н /мм2 Н /мм2
Следовательно, 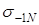 = 39,6 кГ/мм2
. = 39,6 кГ/мм2
.
При реверсе  и, следовательно, опять и, следовательно, опять
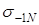 = 39,6 кГ/мм2
= 388 Н/мм2
. = 39,6 кГ/мм2
= 388 Н/мм2
.
10. Коэффициент чувствительности материала зубьев к асимметрии цикла напряжения [I]
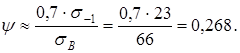
11. Допускаемые напряжения на изгиб зубьев при асимметричных циклах и ограниченной долговечности
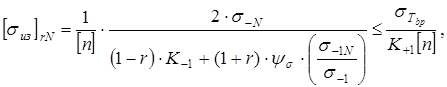 , ,
где [n
]= 1,7ч2— допускаемый коэффициент запаса прочности зубьев на
изгиб.
Принимая для незакаленных зубьев [n
] = 1,7 (отсутствуют закалочные напряжения), находим:
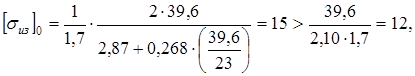
Следовательно
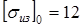 кГ/мм2
= 117 Н/мм2
; кГ/мм2
= 117 Н/мм2
;
при r=-0,5 (реверс момента)
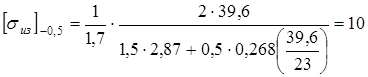 кГ/мм2
<21. кГ/мм2
<21.
Из сопоставления следует, что изгибная прочность зубьев лимируется величиной 
§ 18. Проверка зубьев червячного колеса на изгибную прочность
1. На номинальном режиме
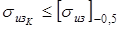 , т.е. 2,2 кГ/мм2
<10. , т.е. 2,2 кГ/мм2
<10.
§ 19. Окончательные основные размеры червячной пары
редуктора
A
= 187,50 мм
; 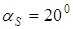 ; ; 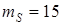 мм; мм;
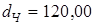 мм; мм;
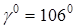 ; ; 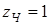 ; ;
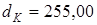 мм; мм;
 ; ; 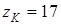 . .
Конструктивная ширина червячного венца b
≈1,08; b
=88; q
=8.
Глава
III
. Расчет конической зубчатой пары
Исходные данные
1. Мощность на ведущем валу W
1
=2,2 квт
.
2. Число оборотов ведущего вала n
1
=5000 об/мин
.
3. Межосевой угол δ
=90°
.
4. Передаточное число пары i
1
=1,72.
5. К.п.д. зубчатой пары η
≈0,98.
6. Коэффициент динамичности внешней нагрузки K
Д
=1,05.
7. Расчетная долговечность N
ц.н
=800 циклов
8. Коэффициент перегрузки при пробуксовке муфты K
пер
=2.
 Рисунок 4 - Кинематическая схема конической пары в 1-й ступени редуктора
§1. Определение угловых скоростей
n
1
=10 000 об/мин;
 об/мин (далее подлежит уточнению). об/мин (далее подлежит уточнению).
§2. Определение крутящих моментов (исходя из полной номинальной загрузки двигателя)
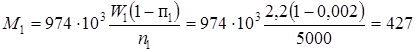 кГмм = кГмм =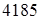 Нмм; Нмм;
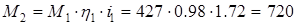 кГмм = кГмм =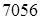 Нмм. Нмм.
§3. Подбор материала и термообработки зубчатых колес
Твердость зубьев шестерен для сближения долговечности шестерни и колеса рекомендуется назначать выше твердости зубьев колес.
Обычно 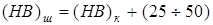 . .
Выбираем материал с высоким пределом выносливости, достаточной твердостью и хорошей ударной вязкостью (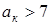 кГм/см2
). кГм/см2
).
С целью сохранения последней у малых зубьев желательно ограничить твердость HB
<400, поскольку применение здесь поверхностей закалки затруднительно.
Этим требованиям удовлетворяет сталь 18ХНВА с соответствующей термообработкой [I] (см. табл. 1).
Таблица 1
| Зубчатые колеса
|
Термообработка
|
σВ
,
кГ/мм2
|
σТ
,
кГ/мм2
|
σ1
,
кГ/мм2
|
НВ
|
Е,
кГ/мм2
|
aк
,
кГ/мм2
|
| Шестерня
Колесо
|
Закалка с низким отпуском
Термоу-
лучшение
|
130
110
|
110
80
|
56
53
|
370+
400
330+
340
|
2,04·104
---,,---
|
12
11
|
Заготовка колес – из проката или штамповки.
§4. Определение числа циклов изменения напряжений зубьев за расчетную долговечность
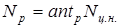 циклов, циклов,
где a
– число зацеплений, проходимых зубом одной и той же
стороной
профиля за 1 оборот;
n
– число оборотов в минуту;
t
p
– расчетная длительность нагружения детали в минутах за
один цикл
эксплуатационной нагрузки.
1. По контактным напряжениям.
При выпуске и уборке закрылков в воздухе в механизме данной схемы работают разные стороны профилей зубьев, поэтому при t
p
=t
°
=0.5 мин
, a
=1 и N
ц.н
=800 находим:
для ведущих зубьев
 циклов; циклов;
для ведомых зубьев
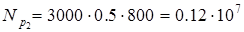 циклов. циклов.
2. По изгибным напряжениям.
Здесь нужно провести проверку дважды: при r
=0 и 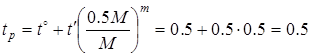 мин. мин.
 циклов; циклов;
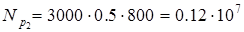 циклов; циклов;
при r=-0.5 (реверс момента) соответственно числу реверсов
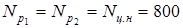 циклов. циклов.
§5. Определение допускаемых контактных напряжений для зубьев [
I
]
Их величины являются функцией твердости и числа циклов напряжения и ограничиваются верхним и нижним пределами :
 кГ/мм2
; кГ/мм2
;  кГ/мм2
. кГ/мм2
.
Из следующей записи условия:
 , ,
где N
p
(по §4, п.1) после числовых подстановок:
для шестерни
 , ,
получаем 68<125<132.
Значит,
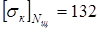 кГ/мм2
= 1294 Н/мм2
; кГ/мм2
= 1294 Н/мм2
;
для колеса
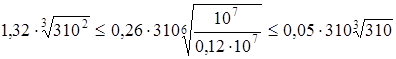 , ,
получаем 68<137>133.
Значит,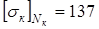 кГ/мм2
=1343 Н/мм2
. кГ/мм2
=1343 Н/мм2
.
Для расчета принимаем меньшее в паре
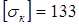 кГ/мм2
= 1303 Н/мм2
. кГ/мм2
= 1303 Н/мм2
.
§6. Предварительный подбор степени точности зацепления
В зубчатых передачах авиационных приборов наиболее распространены 5-я, 6-я, 7-я и 8-я степени точности зацепления в зависимости от окружной скорости и погонной нагрузки на зуб, а значит, и от твердости.
При НВmin
в паре =310 можно принимать 7-ю степень точности [I], но, учитывая значительную ожидаемую скорость (n
1
=10 000 об/мин), задаемся
6-й повышенной степенью точности.
§7. Выбор относительной ширины зубчатых венцов
В узлах авиационных агрегатов обычно применяются зубчатые пары узкого типа как менее чувствительные к приборам валов и сниженной жесткости облегченных корпусов. При малой мощности (1ч5 квт) обычно ψL
≤0,2[I]. Предварительно принимаем ψL
=0,16.
§8. Выбор формы зуба в плане
Ввиду значительной ожидаемой скорости задаемся косым зубом с углом скоса по условию [I]
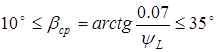 . .
При ψL
=0,16 имеем
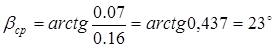 . .
Принимаем  ; ; 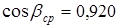 . .
§9. Определение поправочных коэффициентов, влияющих на расчетную величину погонной нагрузки
1. Неравномерность распределения погонной нагрузки по длине зубьев учитывается коэффициентом концентрации 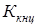 [I] [I]
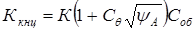 , ,
где К
=1,2 – для косозубых колес;
 =0,45 – для несимметрично расположенного колеса по отношению к =0,45 – для несимметрично расположенного колеса по отношению к
опорам и консольно сидящей шестерни;
Соб
=1 – при ободе с тонким диском.
Подставляя числовые значения, получаем
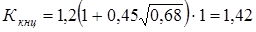 . .
2. Дополнительные динамические нагрузки на зубья в зависимости от окружной скорости, твердости и степени точности, возникающие как следствие погрешностей изготовления зубьев по основному шагу, учитывает скоростной коэффициент [I]
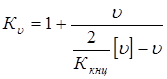 , ,
где  - окружная скорость, а - окружная скорость, а 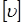 - ее допускаемое значение в данном случае. - ее допускаемое значение в данном случае.
Поскольку величина 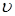 зависит от размеров передачи, которые еще не определены, задаемся в первом приближении зависит от размеров передачи, которые еще не определены, задаемся в первом приближении
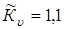 . .
3.Взаимоподдерживающее действие пар зубьев, находящихся в зацеплении, учитывает коэффициент профильного перекрытия К.
Для косых зубьев при расчете их по контактным напряжениям для 6-й степени точности предварительно принимаем [I]
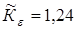 . .
§10. Определение конусного расстояния из расчета на контактную прочность зубьев на номинальном режиме (первое приближение) [
I
]
 мм, мм,
где δ
=90°
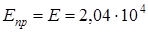 кГ/мм = кГ/мм = Н/мм; Н/мм;
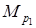 =М1
·Кд
=427·1,05=448 кГмм = =М1
·Кд
=427·1,05=448 кГмм =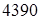 Нмм. Нмм.
Подставляя принятые и найденные входящие сюда величины, получаем
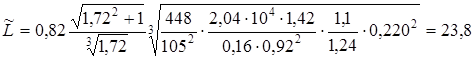 мм. мм.
§11. Проверка выбора степени точности зацепления
1. Ориентировочная окружная скорость в среднем сечении
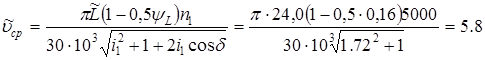 м/сек. м/сек.
2. Предельно допустимое значение окружной скорости для стальных цилиндрических косозубых пар 6-й степени точности, НВmin
=350 и при i
=1ч5[I]
Интерполируем по линейному закону для i1
=1,71:
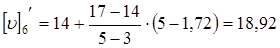 м/сек. м/сек.
С поправкой на твердость НВmin
=310 находим
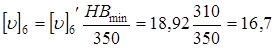 м/сек. м/сек.
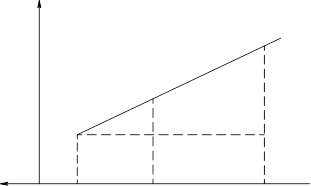 Рисунок 6 - Предельно допустимое значение окружной скорости в зависимости от передаточного числа при 6-й степени точности и НВmin
=350
3. Правильность выбора степени точности проверяем по условию
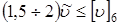 . .
При  м/сек
и среднем значении 1,75 коэффициента запаса на нераскрытие контактов зубьев получаем м/сек
и среднем значении 1,75 коэффициента запаса на нераскрытие контактов зубьев получаем
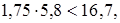 т.е. т.е. 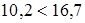 м/сек. м/сек.
Ввиду небольшого повышения (<4%) оставляем пока выбранную в §6 расчета 6-ю степень точности зацепления.
§12. Уточнение межосевого расстояния
1. Скоростной коэффициент во втором приближении
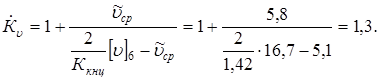
2. Коэффициент профильного перекрытия остается без изменения, так как степень точности осталась прежней:
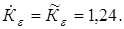
3. Уточненное конусное расстояние (второе приближение)
 мм. мм.
§13. Подбор модуля зубьев
Для обеспечения хорошей плавности зацепления  модуль подбираем по условию [I] модуль подбираем по условию [I]
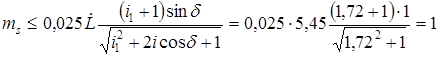 мм. мм.
По ГОСТу 9563-60 принимаем 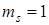 мм. мм.
§14. Выбор числа зубьев колес
При выбранном модуле и найденном межосевом расстоянии числа зубьев определяются геометрическими выражениями:
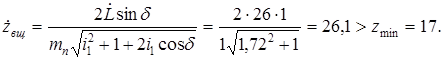
Округляем до целого числа:
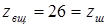 , ,
и далее
 . .
Так же округляем
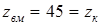 . .
§15. Определение основных размеров зубчатой пары
1. Точное значение конусного расстояния (до сотых долей мм
)
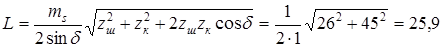 мм. мм.
2. Рабочая ширина зубчатых венцов (до десятых долей мм)
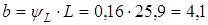 мм. мм.
3. Точные значения делительных диаметров шестерни и колеса (до сотых долей мм
):
 мм; мм;
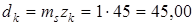 мм. мм.
4. Угол зацепления в среднем торцовом сечении (при 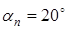 ) )
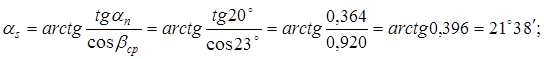
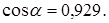
5. Половинные углы начальных конусов φ
1
и φ
2
:
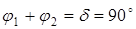 ; ;   ; ;
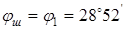 ; ; 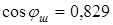 ; ;
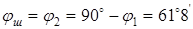 ; ;  . .
§16. Уточнение кинематического расчета
1. Передаточное число 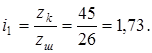
Отклонение от прежнего 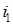 составляет +0,9%, что вполне допустимо (±2- составляет +0,9%, что вполне допустимо (±2-
3%).
2. Число оборотов валов:
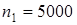 об/мин; об/мин; 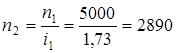 об/мин. об/мин.
3. Фактическая окружная скорость в среднем сечении
Поскольку средний диаметр шестерни найдется из следующего соотношения:
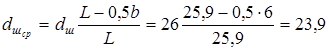 мм
, мм
,
получим
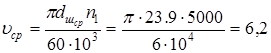 м/сек
. м/сек
.
§17. Повторная проверка выбора степени точности зацепления и коэффициентов К
υ
и К
ε
1. По записи, аналогично как и в §11, п.3, получаем
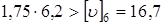 м/сек; м/сек;
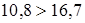 . .
Так как расхождений нет оставляем 8-ю степень.
§18. Проверка полученных размеров конической пары на контактную прочность зубьев [
I
]
 кГ/мм2
. кГ/мм2
.
Подставляя принятые и найденные входящие сюда величины, получим:
1. На номинальном режиме
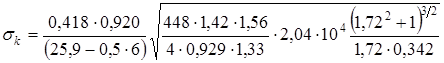 = =
=112 кГ/мм2
<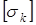 =133 кГ/мм2
= 1274 Н/мм2
. =133 кГ/мм2
= 1274 Н/мм2
.
2. На перегрузочном режиме пробуксовки предохранительной муфты с коэффициентом перегрузки 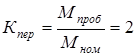 (по исходным данным); (по исходным данным);
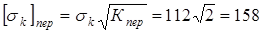 кГ/мм2
= кГ/мм2
=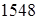 Н/мм2
, Н/мм2
,
что превышает
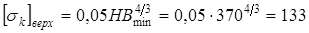 кГ/мм2
=1274 Н/мм2
. кГ/мм2
=1274 Н/мм2
.
Проще всего это можно исправить путем уширения колес.
Исходя из соотношения

получаем новое значение b
'
= 6 мм.
Это означает 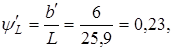 что выполнимо без усложнения конструкции. что выполнимо без усложнения конструкции.
3. Тогда на номинальном режиме получим
при

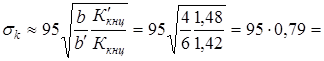
=78 кГ/мм2
< =133 кГ/мм2
, =133 кГ/мм2
,
а на перегрузочном режиме
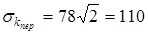 кГ/мм2
=1078 Н/мм2
=1,2 кГ/мм2
=1078 Н/мм2
=1,2 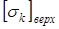 , ,
что вполне допустимо.
В результате принимаем новое значение рабочей ширины зубчатых венцов b
=6 мм.
§19. Определение расчетных изгибных напряжений в зубьях (на номинальном режиме)
1. Эквивалентное число зубьев для цилиндрических косозубых колес
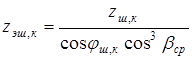 , ,
2. Коэффициент формы профиля зуба
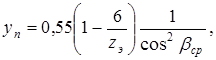

3. Расчетное напряжение изгиба в зубьях шестерни на номинальном режиме [I]
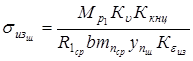 кГ/мм2
, кГ/мм2
,
где 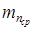 - нормальный модуль в среднем сечении, находящийся из - нормальный модуль в среднем сечении, находящийся из
соотношения
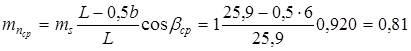 мм; мм;
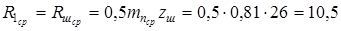 мм; мм;
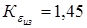 - коэффициент профильного перекрытия для косозубых колес 6-й степени точности при расчете зубьев на изгиб [I]. - коэффициент профильного перекрытия для косозубых колес 6-й степени точности при расчете зубьев на изгиб [I].
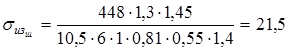 кГ/мм2
= кГ/мм2
=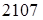 Н/мм2
. Н/мм2
.
4. Расчетное напряжение изгиба в зубьях колеса на номинальном режиме
 кГ/мм2
= кГ/мм2
=  Н/мм2 Н/мм2
§ 20. Допускаемые напряжения зубьев на изгиб
1. Эквивалентное число зубьев по §19, п. 1:
|  Для шестерни Для шестерни
|
Для колеса
|
2. Теоретический коэффициент концентрации напряжений у корня зуба

 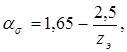
3. Коэффициент чувствительности материала к концентрации напряжений для стали
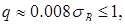

следовательно, 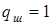 , ,
4. Эффективный коэффициент концентрации напряжений у корня зуба
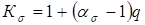 , ,
5. Коэффициент влияния чистоты поверхности у корня зуба (здесь шероховатость часто больше, чем на рабочем профиле)
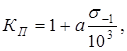
где а
=6, если чистота у корня зуба 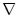 6, 6,
6. Коэффициент качества заготовки из проката или штамповки [I]:
7. Масштабные коэффициенты зуба [I]. При  мм мм

8. Результирующие коэффициенты влияния отличий детали от экспериментального образца материала:
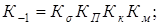
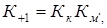
9. Пределы ограниченной выносливости материала зубьев
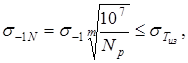
где m
=9ч12;
Np
– по §4, п.2;
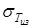 ≈1,2 ≈1,2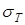 . .

| 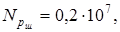
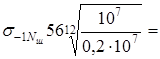
=64 кГ/мм
2
<132.
При реверсе 
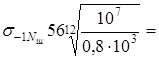
=123 кГ/мм
2
<132.
|
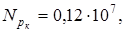
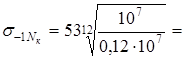
=63 кГ/мм
2
<96.
При реверсе 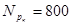
  116>96. 116>96.
Значит, 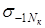 =96 кГ/мм
2
. =96 кГ/мм
2
.
|
Следовательно, 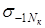 =96 кГ/мм
2
= 940 Н/мм2
. =96 кГ/мм
2
= 940 Н/мм2
.
10. Коэффициенты чувствительности материала зубьев к асимметрии цикла напряжения [I] для сталей
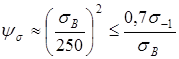 , ,
11. Допускаемые напряжения на изгиб зубьев при асимметричных циклах и ограниченной долговечности [I]
 кГ/мм2
, кГ/мм2
,
где допускаемый коэффициент запаса прочности 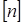 =1,7ч2. =1,7ч2.
Для незакаленных зубьев 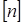 =1,7; =1,7;
для высокозакаленных (низкий отпуск) в результате существенного влияния остаточных закалочных напряжений на прочность зубьев 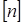 =2. =2.
Принимая в нашем случае для зубьев шестерни 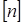 ш
=1,9 и для зубьев колес ш
=1,9 и для зубьев колес 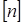 к
=1,8, находим к
=1,8, находим
при r
=0
|  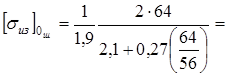
=28 кГ/мм
2
<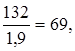
|

=31 кГ/мм
2
<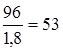 ; ;
|
при r
=-0,5 (реверс момента)
|  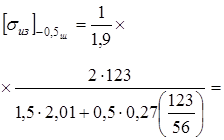
=37 кГ/мм
2
<69.
|
  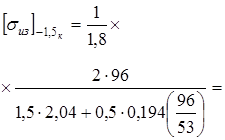
=33 кГ/мм
2
<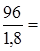 53. 53.
|
Из сравнения следует, что для проверки прочности зубьев на изгиб должны быть взяты
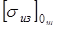 =28 кГ/мм2
= =28 кГ/мм2
=  Н/мм2
и Н/мм2
и 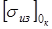 =31 кГ/мм2
= =31 кГ/мм2
=  Н/мм2
. Н/мм2
.
§21. Проверка зубьев на изгибную прочность
1. На номинальном режиме:

| 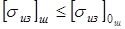 , ,
т.е. 21,5<28 кГ/мм2
|
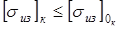 , ,
т.е. 19<30 кГ/мм2
,
|
2. На перегрузочном режиме при пробуксовке муфты:
| 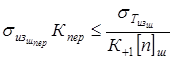 , ,
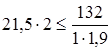 , ,
43<69 кГ/мм2
,
|
 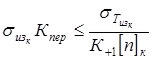 , ,
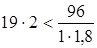 , ,
38<53 кГ/мм2
.
|
§22. Окончательные основные размеры конической пары редуктора
| dш
=26,00 мм;
zш
=26;
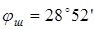 ; ;
|
dк
=45,00мм;
zк
=45;
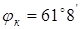 ; ;
|
L=25,9 мм;
b=6,0 мм;
ms
=1 мм;
|
δ=90°
;
αn
=20°
;
βср
=23°
.
|
Степень точности зацепления – 4-я.
Глава
IV
. Расчет выходного вала редуктора
Исходные данные (из предыдущего расчета)
1. Угловая скорость вала n
=10,5 об/мин.
2. Крутящий момент на червячном колесе 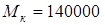 кГмм = кГмм = 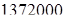 Н. Н.
3. Коэффициент динамичности внешней нагрузки 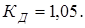
4. Делительные диаметры:
червячного колеса 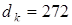 мм, мм,
цепной звездочки 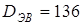 мм. мм.
5. Угол скоса зубьев червячного колеса 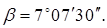
6. Угол зацепления зубьев 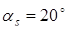 . .
7. Приведенный коэффициент трения скольжения вдоль по винтовой линии
зубьев 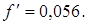
8. Приведенный угол трения 
§1. Определение расчетных величин нагрузок, действующих на вал
1. Расчетный момент на валу
 кГмм = кГмм = 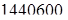 Н/мм. Н/мм.
3. Расчетная окружная сила на колесе
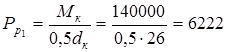 кГ
=
60975 H
. кГ
=
60975 H
.
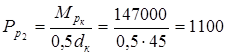 кГ. = 9790 H. кГ. = 9790 H. 4. Расчетная аксиальная сила на колесе
 кГ = кГ =  Н. Н.
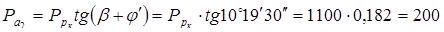 кГ = кГ = 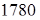 Н. Н.
5. Расчетное распорное усилие в зацеплении
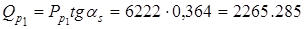 кГ = кГ = 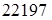 Н, Н,
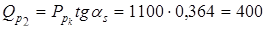 кГ = кГ = 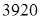 Н. Н.
6. Расчетная окружная сила на цепной звездочке
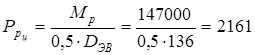 кГ = кГ = 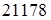 Н. Н.
§2. Выбор материала вала
Для унификации материала возьмем сталь 40ХНА с термоупрочнением, как и для червячного вала. После закалки с высоким отпуском 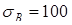 кГ/мм2
= 980 Н/мм2
; кГ/мм2
= 980 Н/мм2
; 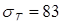 кГ/мм2
= 813 Н/мм2
; кГ/мм2
= 813 Н/мм2
; 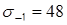 кГ/мм2
= 470Н/мм2
при удовлетворительной вязкости. кГ/мм2
= 470Н/мм2
при удовлетворительной вязкости.
§3. Предварительное определение диаметра и конструктивная разработка вала
1. Для уменьшения веса выполняем вал полым, задавшись относительной величиной диаметра отверстия 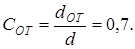
Для наиболее нагруженного участка вала диаметр вала ищем по условию [I]
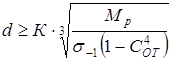 мм, мм,
где 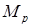 - расчетный момент на валу, кГмм; - расчетный момент на валу, кГмм;
К
– коэффициент, учитывающий влияние расположения зубчатых колес по отношению к подшипникам; для тихоходного вала при консольном расположении цепной звездочки 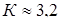 ; ;
 - предел выносливости материала вала, кГ/мм2
. - предел выносливости материала вала, кГ/мм2
.
Подставляя соответствующие числовые значения, получаем
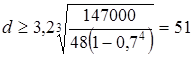 мм. мм.
2. По ГОСТу 6636-60 принимаем для наиболее нагруженного участка вала под подшипником выходного конца 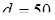 мм. мм.
Задаемся из легкой серии подшипником №7208 со следующими данными [4]:
d
=50
мм; D
=72
мм; В=12
мм.
угол наклона беговой дорожки наружного кольца (угол нормали контакта) 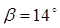 ; ;
коэффициент работоспособности 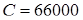 ; ;
допускаемая статическая нагрузка  кГ кГ 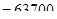 Н; Н;
предельное число оборотов 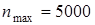 об/мин. об/мин.
§
4. Составление расчетной
схемы вала как балки
и построение
эпюр
нагрузок
и напряжений
Коэффициент равен
к=
1. В плоскости ху
опорные реакции:
из 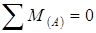
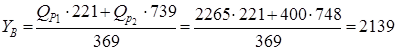 кГ =20962 Н. кГ =20962 Н.
из 
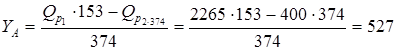 кГ =5164 Н. кГ =5164 Н.
Изгибающие моменты

2. В плоскости zx
:

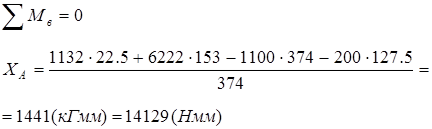
Изгибающие моменты:
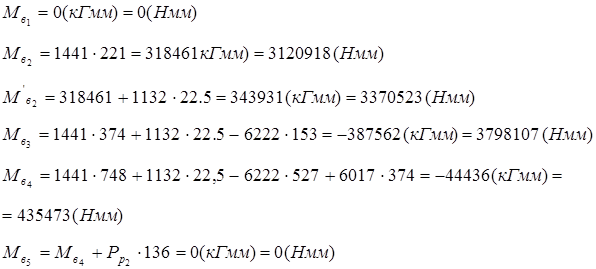
3.Полные реакции и изгибающие моменты:
на опоре A
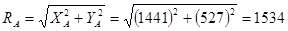 кГ =15033 Н . кГ =15033 Н .
на опоре В
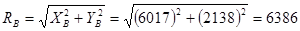 кГ =62583 Н. кГ =62583 Н.
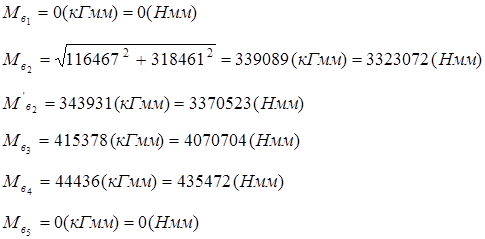
4.Крутящий момент
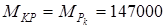 кГмм.= 1440600 Нмм кГмм.= 1440600 Нмм
Считаем, что вдоль по шлицам крутящий момент изменяется линейно.
| Рисунок 7 – Построение эпюр
|
|
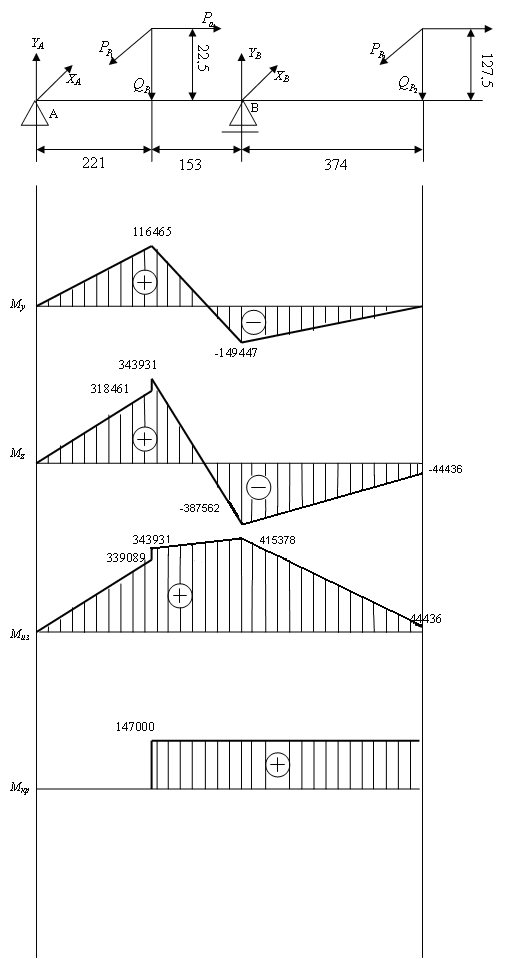 5. Осевая сила.
На тело вала осевая сила в этой конструкции не переходит, а передается через установочное кольцо сразу на внутренне кольцо подшипника В.
6. Строим эпюры напряжений по эпюрам крутящего и изгибающего моментов, используя формулы сопротивления материалов
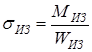 и и 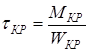 . .
Эпюры напряжений получают скачки в сечениях, где имеют место скачки моментов и скачки диаметров.
Далее на эти эпюры накладываем картину концентрации напряжений.
7. По эпюрам напряжений намечаем два опасных сечения I-I и II-II, по которым следует провести проверочный расчет вала на прочность.
§ 5. Проверочный расчет вала по сечению
I
–
I
1.Геометрические характеристики сечения.
Относительная величина отверстия
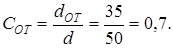
Момент сопротивления сечения при изгибе
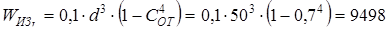 мм3
. мм3
.
Момент сопротивления сечения при кручении
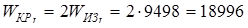 мм3
. мм3
.
2. Внутренние моменты в сечении I – I.
Интерполируя по эпюре 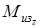 , находим , находим  кГмм.= кГмм.= Нмм Нмм
Интерполируя по эпюре 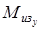 , находим , находим 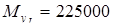 кГмм.=2205000Нмм кГмм.=2205000Нмм
Полный изгибающий момент
 кГмм = 3030160 Нмм. кГмм = 3030160 Нмм.
3.Расчетные напряжения:
изгиба
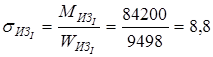 кГ/мм2
=86,24 Н/мм2
. кГ/мм2
=86,24 Н/мм2
.
кручения
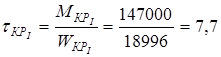 кГ/мм2
=75,46 Н/мм2
. кГ/мм2
=75,46 Н/мм2
.
4. Коэффициенты влияния отличий детали от образца материала.
Эффективные коэффициенты концентрации напряжений для валов с галтельными переходами [I].
Сначала находим по соответствующему графику теоретический коэффициент
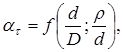
где 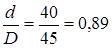 и и 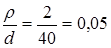 ; следовательно, ; следовательно, 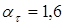 . .
Затем определяем коэффициент чувствительности материала к концентрации напряжений для сталей:
 т.е т.е
 . .
Далее находим эффективные коэффициенты концентрации
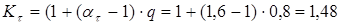
по приближённой формуле

Коэффициент чистоты поверхности около сечения I – I.
При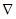 8 коэффициент шероховатости а
= 4 и 8 коэффициент шероховатости а
= 4 и
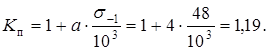
Коэффициент качества заготовки из проката с последующей обработкой
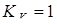 . .
Масштабные коэффициенты находим по экспериментальным кривым на рис. 17 и 18 [I] интерполяций для 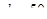 мм
: мм
:
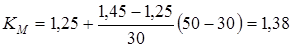 ; ;
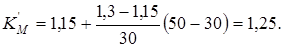
Результирующие коэффициенты влияния отличий детали от образца материала:
при  при расчете на изгиб при расчете на изгиб
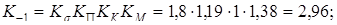
при расчете на кручение

и при 
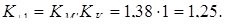
  | Рисунок 8 - Зависимость масштабного коэффициента от размера расчетного сечения (циклическая прочность).
|
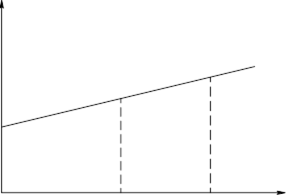
Рисунок 9 - Зависимость масштабного коэффициента от размера расчетного сечения (статическая прочность).
|
5. Пределы ограниченной выносливости материала вала.
По изгибу
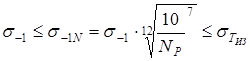 , ,
где кГ/мм2
и число циклов напряжений изгиба кГ/мм2
и число циклов напряжений изгиба
вала за расчетную долговечность
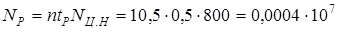 . .
Численные подстановки дают
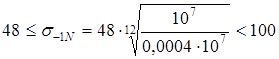 , т.е. , т.е. 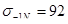 кГ/мм2
=901,6 Н/мм2
. кГ/мм2
=901,6 Н/мм2
.
По кручению с реверсом момента при числе реверсов
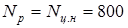
 , ,
где 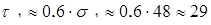 кГ/мм2
= 284 Н/мм2
; кГ/мм2
= 284 Н/мм2
;
 кГ/мм2
=490 Н/мм2. кГ/мм2
=490 Н/мм2.
Численно
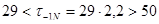 кГ/мм2
,т.е. кГ/мм2
,т.е.  кГ/мм2
=490 Н/мм2
. кГ/мм2
=490 Н/мм2
.
6. Коэффициент чувствительности материала к асимметрии цикла напряжения:
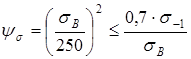 ; ; 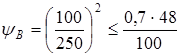 ; ;
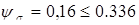 ; ; 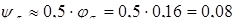 . .
7. Предельные напряжения изгиба и кручения для сечения I-I вала:
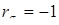 ; ;  кГ/мм2
=294 Н/мм2
. кГ/мм2
=294 Н/мм2
.
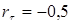 ; ; 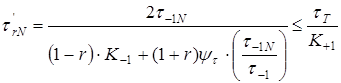 ; ;
 кГ/мм2
<41 кГ/мм2
<41
8. Коэффициенты запасов прочности по сечению I-I вала на номинальном режиме:
по изгибу
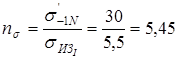 ; ;
по кручению
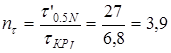 . .
Результативный запас прочности по сечению I-I вала
 . .
§6. Проверочный расчет вала по сечению
II
-
II
Расчет шлицевого участка на изгиб ведут по среднему диаметру 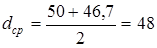 мм; а на кручение – по внутреннему диаметру мм; а на кручение – по внутреннему диаметру 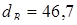 мм
, поскольку выступы принимают весьма малое участие в передаче крутящего момента. мм
, поскольку выступы принимают весьма малое участие в передаче крутящего момента.
1. Геометрические характеристики сечения.
Момент сопротивления сечения при изгибе
при 
 мм3
. мм3
.
Момент сопротивления сечения при кручении
при 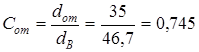
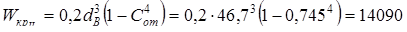 мм3
. мм3
.
2. Внутренние моменты в сечении II-II.
Интерполируя по эпюре  , находим , находим  кГмм=415520 Нмм в то время как по эпюре кГмм=415520 Нмм в то время как по эпюре 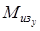 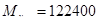 кГмм= 1199520 Нмм. кГмм= 1199520 Нмм.
Полный изгибающий момент
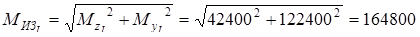 кГмм = 1615040 Нмм. кГмм = 1615040 Нмм.
3. Расчетные напряжения:
изгиба
 кГ/мм2
= 51,94 Н/мм2
. кГ/мм2
= 51,94 Н/мм2
.
кручения
 кГ/мм2
= 101,9 Н/мм2
. кГ/мм2
= 101,9 Н/мм2
.
4. Коэффициенты влияния отличий детали от образца материала.
Эффективные коэффициенты концентрации напряжений во впадинах шлицов по сечению II-II при плавном выходе впадин:
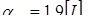 
 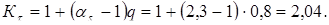
Коэффициент чистоты поверхности около сечения II-II.
Соответственно  имеем имеем  и и
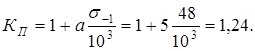
Коэффициент качества заготовки из проката с последующей обработкой 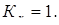
Масштабные коэффициенты.
Интерполирование по кривым дает:
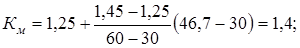
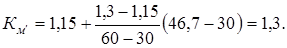
Результирующие коэффициенты влияния отличий детали от образца материала:
при  при расчете на изгиб при расчете на изгиб
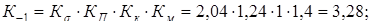
при расчете на кручение

при 
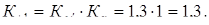
5. Пределы ограниченной выносливости материала вала.
Как и в расчете по сечению I-I,
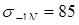 кГ/мм2
; кГ/мм2
; 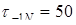 кГ/мм2
. кГ/мм2
.
6. Коэффициент чувствительности материала к асимметрии цикла напряжения.
Как и в расчете по сечению I-I,
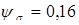 ; ; 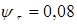 . .
7. Предельные напряжения изгиба и кручения для сечения II-II:
 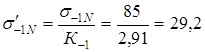 кГ/мм2
= 286,16 Н/мм2
. кГ/мм2
= 286,16 Н/мм2
.
 ; ; 
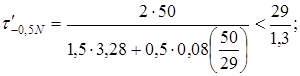 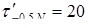 кГ/мм2
<24. кГ/мм2
<24.
8. Коэффициенты запасов прочности по сечению II-II:
по изгибу
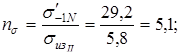
по кручению
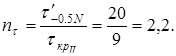
Результативный запас прочности по сечению II-II вала
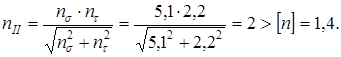
Глава
V
. Проверка подшипников выходного вала на долговечность и на перегрузку
Исходные данные (из расчета вала) (рис. 10)

Рисунок 10 - Силовая схема для расчета подшипников вала.
1. Опорные реакции: 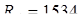 кГ; кГ; 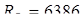 кГ. кГ.
2. Осевая сила  кГ= 80360 Н. кГ= 80360 Н.
3. Угловая скорость вала n
=10,5 об/мин.
4. Коэффициент динамичности внешней нагрузки 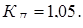
Необходимые данные взятого подшипника приведены в конструктивной
разработке вала.
В частности, 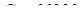 - коэффициент работоспособности подшипника; - коэффициент работоспособности подшипника;
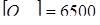 кГ
=63700 Н –допускаемая статическая нагрузка на подшипник; кГ
=63700 Н –допускаемая статическая нагрузка на подшипник;
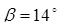 - угол нормали контакта роликов по наружному кольцу. - угол нормали контакта роликов по наружному кольцу.
§1. Определение результирующей осевой нагрузки на подшипник

Рисунок 11 - Схема для определения результирующей осевой нагрузки на подшипник.
1. Аксиальные составляющие, возникающие в подшипниках:

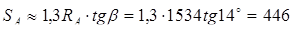 кГ = 4371 Н. кГ = 4371 Н.
 кГ = 18185 Н. кГ = 18185 Н.
2. Результирующая осевая нагрузка
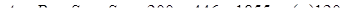 кГ = -11848 Н. кГ = -11848 Н.
Знак (-) указывает на направление А
навстречу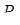 . Следовательно, вся осевая нагрузка воспринимается левым подшипником А
. . Следовательно, вся осевая нагрузка воспринимается левым подшипником А
.
§2. Определение поправочных коэффициентов к нагрузкам на подшипники [4]
1. Коэффициент приведения осевой нагрузки на подшипник к радиальной.
Для роликоподшипников конических легкой серии находим по таблице
каталога (справочника) 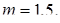
2. Коэффициент кинематический.
При вращении внутреннего кольца

3. Коэффициент динамичности нагрузки
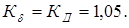
4. Коэффициент температурный.
При работе подшипника в условиях рабочей температуры <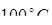
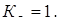
§3. Расчет приведенных радиальных нагрузок на подшипники

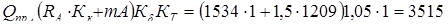 кГ
= 34445 Н
,
кГ
= 34445 Н
,
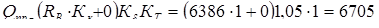 кГ
= 65712 Н.
кГ
= 65712 Н.
Отсюда следует, что проверку достаточно провести по более нагруженному подшипнику на опоре В
, поскольку сами подшипники взяты одинаковыми.
§4. Определение ожидаемой долговечности подшипника
Из выражения для коэффициента работоспособности согласно каталогу
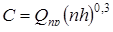
находим
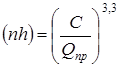 ; ;

откуда 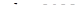 и и 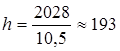 часа. часа.
§5. Определение минимально необходимой долговечности
подшипника
Для подшипников качения согласно нагрузочному графику за один цикл эксплуатационной нагрузки
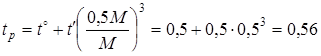 мин. мин.
За расчетную долговечность 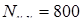 циклов циклов
 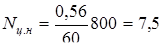 часов. часов.
§6. Условие по долговечности
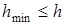
удовлетворяется с огромным запасом (7,5<<193), но на более легкий подшипник перейти нельзя, если допускаемая статическая нагрузка для него согласно каталогу меньше 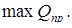
Заключение
В данной курсовой работе был разработан конический редуктор электромеханизма подъемника створок колеса шасси. В процессе проектирования были рассчитаны:
конические зубчатые пары;
| d
ш
=26,00 мм;
zш
=26;
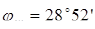 ; ;
|
d
к
=45,00 мм;
z
к
=45;
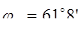 ; ;
|
L
=25,9 мм;
b
=6,0 мм;
m
s
=1 мм;
|
δ
=90°
;
α
n
=20°
;
βср
=23.
|
червячные передачи;
A
= 187,00 мм ; 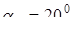 ; ; 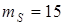 мм; мм;
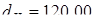 мм; мм;
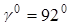 ; ; 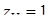 ; ;
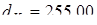 мм; мм;
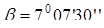 ; ; 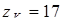 . .
определена математическая модель редуктора, а также выходной вал редуктора и проверены подшипники выходного вала на долговечность
Литература
1. «Сборник заданий на курсовое проектирование деталей машин, приборов и механизмов радиоаппаратуры». Под редакцией Хринеченко Е. П. М. МАИ 1973г.
2. Куприянов В. И. Рощин Г. И. «Методическое пособие для курсового проектирования по деталям механизма». М. МАИ, 1975г.
3. «Расчёт деталей механизмов и машин». под редакцией Герлаха Л. Г. М. МАИ, 1971г.
4. Шейнберг А. Е. «Курсовое проектирование деталей машин». Калиниград. «Янтарный сказ», 2005г.
5. Методическое пособие по дипломному и курсовому проектированию для специальности «Авиационные приборы и ИВК» и «Информационно-измерительная техника и технологии»/ НГТУ; Сост.: Карасёва Т. В., Миркин Я. Л.. Н. Новгород, 2005г.
6. «Конструирование узлов и деталей авиационных приборов». Учебное пособие под редакцией Волгина В. В. М. МАИ, 1988г.
|