Быстрое преобразование Фурье (БПФ) - это алгоритм вычисления преобразования Фурье для дискретного случая. В отличие от простейшего алгоритма, который имеет сложность порядка O(N2
), БПФ имеет сложность всего лишь O(Nlog2
N). Алгоритм БПФ был впервые опубликован в 1965 году в статье Кули (Cooly) и Тьюки (Tukey).
Данное пособие содержит исходный код работающей программы для вычисления БПФ, подробное объяснение принципа ее работы и теоретическое обоснование. Все это можно найти и на других ресурсах, но трудно найти именно в таком комплекте: и программа, и объяснения, и теория, и на русском языке.
Если у вас нет времени и желания разбираться с теорией, то можете сразу скопировать текст программы на C++. Здесь находится заголовочный файл fft.h и исходник fft.cpp для быстрого преобразования Фурье для числа отсчетов, равного степени двойки. Вызывать надо функцию fft. А здесь находится заголовочный файл и исходник для произвольного (!) числа отсчетов. Он чуть медленнее, но скорость там тоже порядка Nlog2
N. Вызывать надо функцию universal_fft.
Определение 1
.
Дана конечная последовательность x0
, x1
, x2
,...,xN-1
(в общем случае комплексных). Дискретное преобразование Фурье (ДПФ) заключается в поиске другой последовательности X0
, X1
, X2
,...,XN-1
элементы которой вычисляются по формуле:
 (1). (1).
Определение 2
.
Дана конечная последовательность X0
, X1
, X2
,...,XN-1
(в общем случае комплексных). Обратное дискретное преобразование Фурье (ДПФ) заключается в поиске другой последовательности x0
, x1
, x2
,...,xN-1
элементы которой вычисляются по формуле:
 (2). (2).
Основным свойством этих преобразований (которое доказывается в соответствующих разделах математики) является тот факт, что из последовательности {x} получается (при прямом преобразовании) последовательность {X}, а если потом применить к {X} обратное преобразование, то снова получится исходная последовательность {x}.
Определение 3
.
Величина

называется поворачивающим множителем
.
Рассмотрим ряд свойств поворачивающих множителей, которые нам понадобятся в дальнейшем.
Верхняя цифра в поворачивающем множителе не является индексом, это - степень. Поэтому, когда она равна единице, мы не будем ее писать:
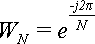
Прямое преобразование Фурье можно выразить через поворачивающие множители. В результате формула (1) примет вид:
 (3). (3).
Эти коэффициенты действительно оправдывают свое название. Нарисуем на комплексной плоскости любое комплексное число, в виде вектора, исходящего из начала координат. Представим это комплексное число в показательной форме: rejφ
, где r - модуль числа, а φ - аргумент. Модуль соответствует длине вектора, а аргумент - углу поворота:

Теперь возьмем какой-нибудь поворачивающий множитель  . Его модуль равен единице, а фаза - 2π/N. Как известно, при умножении комплексных чисел, представленных в показательной форме, их модули перемножаются, а аргументы суммируются. Тогда умножение исходного числа на поворачивающий множитель не изменит длину вектора, но изменит его угол. То есть, произойдет поворот
вектора на угол 2π/N (см. предыдущий рисунок).
. Его модуль равен единице, а фаза - 2π/N. Как известно, при умножении комплексных чисел, представленных в показательной форме, их модули перемножаются, а аргументы суммируются. Тогда умножение исходного числа на поворачивающий множитель не изменит длину вектора, но изменит его угол. То есть, произойдет поворот
вектора на угол 2π/N (см. предыдущий рисунок).
Если теперь посмотреть на формулу (3), то станет ясен геометрический смысл преобразования Фурье: он состоит в том, чтобы представить N комплексных чисел-векторов из набора {x}, каждое в виде суммы векторов из набора {X}, повернутых на углы, кратные 2π/N.
Теорема 0
.
Если комплексное число представлено в виде e j2πN
, где N - целое, то это число e j2πN
= 1.
Доказательство
:
По формуле Эйлера, и ввиду периодичности синуса и косинуса:
e j2
π
N
= cos(2πN) + j sin(2πN) = cos 0 + j sin 0 = 1 + j0 = 1
Теорема 1
.
Величина  периодична по k и по n с периодом N. То есть, для любых целых l и m выполняется равенство:
периодична по k и по n с периодом N. То есть, для любых целых l и m выполняется равенство:
 (4). (4).
Доказательство
:
 (5) (5)
Величина -h = -(nl+mk+mlN) - целая, так как все множители целые, и все слагаемые целые. Значит, мы можем применить Теорему 0:

Что и требовалось доказать по (4).
Теорема 2
.
Для величины  справедлива формула:
справедлива формула:

Доказательство
:

Алгоритм быстрого преобразования Фурье (БПФ) - это оптимизированный по скорости способ вычисления ДПФ. Основная идея заключается в двух пунктах.
- Необходимо разделить сумму (1) из N слагаемых на две суммы по N/2 слагаемых, и вычислить их по отдельности. Для вычисления каждой из подсумм, надо их тоже разделить на две и т.д.
- Необходимо повторно использовать уже вычисленные слагаемые.
Применяют либо "прореживание по времени" (когда в первую сумму попадают слагаемые с четными номерами, а во вторую - с нечетными), либо "прореживание по частоте" (когда в первую сумму попадают первые N/2 слагаемых, а во вторую - остальные). Оба варианта равноценны. В силу специфики алгоритма приходится применять только N, являющиеся степенями 2. Рассмотрим случай прореживания по времени.
Теорема 3
.
Определим еще две последовательности: {x[even]
} и {x[odd]
} через последовательность {x} следующим образом:
x[even]n
= x2n
,
x[odd]n
= x2n+1
, (6)
n = 0, 1,..., N/2-1
Пусть к этим последовательностям применены ДПФ и получены результаты в виде двух новых последовательностей {X[even]
} и {X[odd]
} по N/2 элементов в каждой.
Утверждается, что элементы последовательности {X} можно выразить через элементы последовательностей {X[even]
} и {X[odd]
} по формуле:
 (7). (7).
Доказательство
:
Начинаем от формулы (2), в которую подставляем равенства из (6):
 (8) (8)
Теперь обратим внимание на то, что:
 (9) (9)
Подставляя (9) в (8) получаем:
 (10) (10)
Сравним с формулами для X[even]k
и X[odd]k
при k = 0,1,…,N/2-1:
 (11) (11)
Подставляя (11) в (10) получим первую часть формулы (7):

Это будет верно при k = 0,1,…,N/2-1.
Согласно теореме 1:
 (12) (12)
Подставим (12) в (10), и заменим  по теореме 2:
по теореме 2:
 (13) (13)
Для k = N/2,…,N-1 по формуле (2):
 (14) (14)
Подставляем (14) в (13):

Эта формула верна для k = N/2,…,N-1 и, соответственно, (k - N/2) = 0,1,…,N/2-1 и представляет собой вторую и последнюю часть утверждения (7), которое надо было доказать.
Формула (7) позволяет сократить число умножений вдвое (не считая умножений при вычислении X[even]k
и X [odd]k
), если вычислять Xk
не последовательно от 0 до N - 1, а попарно: X0
и XN/2
, X1
и XN/2+1
,..., XN/2-1
и XN
. Пары образуются по принципу: Xk
и XN/2+k
.
Теорема 4
.
ДПФ можно вычислить также по формуле:
 (15) (15)
Доказательство
:
Согласно второй части формулы (7), получим:

Это доказывает второе равенство в утверждении теоремы, а первое уже доказано в теореме 3.
Также по этой теореме видно, что отпадает необходимость хранить вычисленные X[even]k
и X[odd]k
после использования при вычислении очередной пары и одно вычисление  можно использовать для вычисления двух элементов последовательности {X}.
можно использовать для вычисления двух элементов последовательности {X}.
На этом шаге будет выполнено N/2 умножений комплексных чисел. Если мы применим ту же схему для вычисления последовательностей {X[even]
} и {X[odd]
}, то каждая из них потребует N/4 умножений, итого еще N/2. Продолжая далее в том же духе log2
N раз, дойдем до сумм, состоящих всего из одного слагаемого, так что общее количество умножений окажется равно (N/2)log2
N, что явно лучше, чем N2
умножений по формуле (2).
Рассмотрим БПФ для разных N. Для ясности добавим еще один нижний индекс, который будет указывать общее количество элементов последовательности, к которой этот элемент принадлежит. То есть X{R}k
- это k-й элемент последовательности {X{R}
} из R элементов. X{R}[even]k
- это k-й элемент последовательности {X{R}[even]
} из R элементов, вычисленный по четным элементам последовательности {X{2R}
}. X{R}[odd]k
- это k-й элемент последовательности {X{R}[odd]
}, вычисленный по нечетным элементам последовательности {X{2R}
}.
В вырожденном случае, когда слагаемое всего одно (N = 1) формула (1) упрощается до:
 , ,
Поскольку в данном случае k может быть равно только 0, то X{1}0
= x{1}0
, то есть, ДПФ над одним числом дает это же самое число.
Для N = 2 по теореме 4 получим:

Для N = 4 по теореме 4 получим:

Отсюда видно, что если элементы исходной последовательности были действительными, то при увеличении N элементы ДПФ становятся комплексными.
Для N = 8 по теореме 4 получим:

Обратите внимание, что на предыдущем шаге мы использовали степени W4
, а на этом - степени W8
. Лишних вычислений можно было бы избежать, если учесть тот факт, что

Тогда формулы для N=4 будут использовать те же W-множители, что и формулы для N=8:

Подведем итог:
В основе алгоритма БПФ лежат следующие формулы:
 (16) (16)
Теперь рассмотрим конкретную реализацию БПФ. Пусть имеется N=2T
элементов последовательности x{N}
и надо получить последовательность X{N}
. Прежде всего, нам придется разделить x{N}
на две последовательности: четные и нечетные элементы. Затем точно так же поступить с каждой последовательностью. Этот итерационный процесс закончится, когда останутся последовательности длиной по 2 элемента. Пример процесса для N=16 показан ниже:

Итого выполняется (log2
N)-1 итераций.
Рассмотрим двоичное представление номеров элементов и занимаемых ими мест. Элемент с номером 0 (двоичное 0000) после всех перестановок занимает позицию 0 (0000), элемент 8 (1000) - позицию 1 (0001), элемент 4 (0100) - позицию 2 (0010), элемент 12 (1100) - позицию 3 (0011). И так далее. Нетрудно заметить связь между двоичным представлением позиции до перестановок и после всех перестановок: они зеркально симметричны. Двоичное представление конечной позиции получается из двоичного представления начальной позиции перестановкой битов в обратном порядке. И наоборот.
Этот факт не является случайностью для конкретного N=16, а является закономерностью. На первом шаге четные элементы с номером n переместились в позицию n/2, а нечетные из позиции в позицию N/2+(n-1)/2. Где n=0,1,…,N-1. Таким образом, новая позиция вычисляется из старой позиции с помощью функции:
ror(n,N) = [n/2] + N{n/2}
Здесь как обычно [x] означает целую часть числа, а {x} - дробную.
В ассемблере эта операция называется циклическим сдвигом вправо (ror)
, если N - это степень двойки. Название операции происходит из того факта, что берется двоичное представление числа n, затем все биты, кроме младшего (самого правого) перемещаются на 1 позицию вправо. А младший бит перемещается на освободившееся место самого старшего (самого левого) бита.

рис. 1
Дальнейшие разбиения выполняются аналогично. На каждом следующем шаге количество последовательностей удваивается, а число элементов в каждой из них уменьшается вдвое. Операции ror подвергаются уже не все биты, а только несколько младших (правых). Старшие же j-1 битов остаются нетронутыми (зафиксированными), где j - номер шага:

рис. 2
Что происходит с номерами позиций при таких последовательных операциях? Давайте проследим за произвольным битом номера позиции. Пусть этот бит находился в j-м двоичном разряде, если за 0-й разряд принять самый младший (самый правый). Бит будет последовательно сдвигаться вправо на каждом шаге до тех пор, пока не окажется в самой правой позиции. Это случится после j-го шага. На следующем, j+1-м шаге будет зафиксировано j старших битов и тот бит, за которым мы следим, переместится в разряд с номером T-j-1. После чего окажется зафиксированным и останется на месте. Но именно такое перемещение - из разряда j в разряд T-j-1 и необходимо для зеркальной перестановки бит. Что и требовалось доказать.
Теперь, мы убедились в том, что перестановка элементов действительно осуществляется по принципу, при котором в номерах позиций происходит в свою очередь другая перестановка: зеркальная перестановка двоичных разрядов. Это позволит нам получить простой алгоритм:
for(I = 1; I < N-1; I++){ J = reverse(I,T); // reverse переставляет биты в I в обратном порядке if (I >= J) // пропустить уже переставленные conitnue; S = x[I]; x[I] = x[J]; x[J] = S; // перестановка элементов xI и xJ}Некоторую проблему представляет собой операция обратной перестановки бит номера позиции reverse(), которая не реализована ни в популярной архитектуре Intel, ни в наиболее распространенных языках программирования. Приходится реализовывать ее через другие битовые операции. Ниже приведен алгоритм функции перестановки T младших битов в числе I:
unsigned int reverse(unsigned int I, int T){ int Shift = T - 1; unsigned int LowMask = 1; unsigned int HighMask = 1 << Shift; unsigned int R; for(R = 0; Shift >= 0; LowMask <<= 1, HighMask >>= 1, Shift -= 2) R |= ((I & LowMask) << Shift) | ((I & HighMask) >> Shift);return R;}Пояснения к алгоритму. В переменных LowMask и HighMask хранятся маски, выделяющие два переставляемых бита. Первая маска в двоичном представлении выглядит как 0000…001 и в цикле изменяется, сдвигая единицу каждый раз на 1 разряд влево:
0000...0010000...0100000...100...Вторая маска (HighMask) принимает последовательно значения:
1000...0000100...0000010...000..., каждую итерацию сдвигая единичный бит на 1 разряд вправо. Эти два сдвига осуществляются инструкциями LowMask <<= 1 и HighMask >>= 1.
Переменная Shift показывает расстояние (в разрядах) между переставляемыми битами. Сначала оно равно T-1 и каждую итерацию уменьшается на 2. Цикл прекращается, когда расстояние становится меньше или равно нулю.
Операция I & LowMask выделяет первый бит, затем он сдвигается на место второго (<<Shift). Операция I & HighMask выделяет второй бит, затем он сдвигается на место первого (>>Shift). После чего оба бита записываются в переменную R операцией "|".
Вместо того чтобы переставлять биты позиций местами, можно применить и другой метод. Для этого надо вести отсчет 0,1,2,…,N/2-1 уже с обратным следованием битов. Опять-таки, ни в ассемблере Intel, ни в распространенных языках программирования не реализованы операции над обратным битовым представлением. Но алгоритм приращения на единицу известен, и его можно реализовать программно. Вот пример для T=4.
I = 0;J = 0;for(J1 = 0; J1 < 2; J4++, J ^= 1)for(J2 = 0; J2 < 2; J3++, J ^= 2) for(J4 = 0; J4 < 2; J4++, J ^= 4) for(J8 = 0; J8 < 2; J8++, J ^= 8) { if (I < J){ S = x[I]; x[I] = x[J]; x[J] = S; // перестановка элементов xIи xJ } I++; }В этом алгоритме используется тот общеизвестный факт, что при увеличении числа от 0 до бесконечности (с приращением на единицу) каждый бит меняется с 0 на 1 и обратно с определенной периодичностью: младший бит - каждый раз, следующий - каждый второй раз, следующий - каждый четвертый и так далее.
Эта периодичность реализована в виде T вложенных циклов, в каждом из которых один из битов позиции J переключается туда и обратно с помощью операции XOR (В C/C++ она записывается как ^=). Позиция I использует обычный инкремент I++, уже встроенный в язык программирования.
Данный алгоритм имеет тот недостаток, что требует разного числа вложенных циклов в зависимости от T. На практике это не очень плохо, поскольку T обычно ограничено некоторым разумным пределом (16..20), так что можно написать столько вариантов алгоритма, сколько нужно. Тем не менее, это делает программу громоздкой. Ниже я предлагаю вариант этого алгоритма, который эмулирует вложенные циклы через стеки Index и Mask.
int Index[MAX_T];int Mask[MAX_T];int R;for(I = 0; I < T; I++){ Index[I] = 0; Mask[I] = 1 << (T - I - 1);}J = 0;for(I = 0; I < N; I++){ if (I < J){ S = x[I]; x[I] = x[J]; x[J] = S; // перестановка элементов xI и xJ} for(R = 0; R < T; R++) { J ^= Mask[R]; if (Index[R] ^= 1) // эквивалентно Index[R] ^= 1; if (Index[R] != 0)break; }}Величина MAX_T определяет максимальное значение для T и в наихудшем случае равна разрядности целочисленных переменных ЭВМ. Этот алгоритм, может быть, чуть медленнее, чем предыдущий, но дает экономию по объему кода.
И, наконец, последний алгоритм. Он использует классический подход к многоразрядным битовым операциям: надо разделить 32-бита на 4 байта, выполнить перестановку в каждом из них, после чего переставить сами байты.
Перестановку бит в одном байте уже можно делать по таблице. Для нее нужно заранее приготовить массив reverse256 из 256 элементов. Этот массив будет содержать 8-битовые числа. Записываем туда числа от 0 до 255 и переставляем в каждом порядок битов.
Теперь этот массив применим для последней реализации функции reverse:
unsigned int reverse(unsigned int I, int T){ unsigned int R; unsigned char *Ic = (unsigned char*) &I; unsigned char *Rc = (unsigned char*) &R; Rc[0] = reverse256[Ic[3]]; Rc[1] = reverse256[Ic[2]]; Rc[2] = reverse256[Ic[1]]; Rc[3] = reverse256[Ic[0]];R >>= (32 - T); Return R;}Обращения к массиву reverse256 переставляют в обратном порядке биты в каждом байте. Указатели Ic и Ir позволяют обратиться к отдельным байтам 32-битных чисел I и R и переставить в обратном порядке байты. Сдвиг числа R вправо в конце алгоритма устраняет различия между перестановкой 32 бит и перестановкой T бит. Ниже приводится наглядная геометрическая иллюстрация алгоритма, где стрелками показаны перестановки битов, байтов и сдвиг.

рис. 3
Оценим сложность описанных алгоритмов. Понятно, что все они пропорциональны N с каким-то коэффициентом. Точное значение коэффициента зависит от конкретной ЭВМ. Во всех случаях мы имеем N перестановок со сравнением I и J, которое предотвращает повторную перестановку некоторых элементов. Рядом присутствует некоторый обрамляющий код, применяющий достаточно быстрые операции над целыми числами: присваивания, сравнения, индексации, битовые операциии и условные переходы. Среди них в архитектуре Intel наиболее накладны переходы. Поэтому я бы рекомендовал последний алгоритм. Он содержит всего N переходов, а не 2N как в алгоритме со вложенными циклами или их эмуляцией и не NT как в самом первом алгоритме.
С другой стороны, предварительная перестановка занимает мало времени по сравнению с последующими операциями, использующими (N/2)log2
N умножений комплексных чисел. В таком случае тоже есть смысл выбрать не самый короткий, но самый простой и наглядный алгоритм - последний описанный. Вот его окончательный вид с небольшой оптимизацией:
static unsigned char reverse256[]= { 0x00, 0x80, 0x40, 0xC0, 0x20, 0xA0, 0x60, 0xE0,0x10, 0x90, 0x50, 0xD0, 0x30, 0xB0, 0x70, 0xF0,0x08, 0x88, 0x48, 0xC8, 0x28, 0xA8, 0x68, 0xE8, 0x18, 0x98, 0x58, 0xD8, 0x38, 0xB8, 0x78, 0xF8, 0x04, 0x84, 0x44, 0xC4, 0x24, 0xA4, 0x64, 0xE4, 0x14, 0x94, 0x54, 0xD4, 0x34, 0xB4, 0x74, 0xF4, 0x0C, 0x8C, 0x4C, 0xCC, 0x2C, 0xAC, 0x6C, 0xEC,0x1C, 0x9C, 0x5C, 0xDC, 0x3C, 0xBC, 0x7C, 0xFC,0x02, 0x82, 0x42, 0xC2, 0x22, 0xA2, 0x62, 0xE2, 0x12, 0x92, 0x52, 0xD2, 0x32, 0xB2, 0x72, 0xF2, 0x0A, 0x8A, 0x4A, 0xCA, 0x2A, 0xAA, 0x6A, 0xEA, 0x1A, 0x9A, 0x5A, 0xDA, 0x3A, 0xBA, 0x7A, 0xFA, 0x06, 0x86, 0x46, 0xC6, 0x26, 0xA6, 0x66, 0xE6, 0x16, 0x96, 0x56, 0xD6, 0x36, 0xB6, 0x76, 0xF6, 0x0E, 0x8E, 0x4E, 0xCE, 0x2E, 0xAE, 0x6E, 0xEE, 0x1E, 0x9E, 0x5E, 0xDE, 0x3E, 0xBE, 0x7E, 0xFE, 0x01, 0x81, 0x41, 0xC1, 0x21, 0xA1, 0x61, 0xE1,0x11, 0x91, 0x51, 0xD1, 0x31, 0xB1, 0x71, 0xF1,0x09, 0x89, 0x49, 0xC9, 0x29, 0xA9, 0x69, 0xE9, 0x19, 0x99, 0x59, 0xD9, 0x39, 0xB9, 0x79, 0xF9, 0x05, 0x85, 0x45, 0xC5, 0x25, 0xA5, 0x65, 0xE5, 0x15, 0x95, 0x55, 0xD5, 0x35, 0xB5, 0x75, 0xF5, 0x0D, 0x8D, 0x4D, 0xCD, 0x2D, 0xAD, 0x6D, 0xED, 0x1D, 0x9D, 0x5D, 0xDD, 0x3D, 0xBD, 0x7D, 0xFD, 0x03, 0x83, 0x43, 0xC3, 0x23, 0xA3, 0x63, 0xE3,0x13, 0x93, 0x53, 0xD3, 0x33, 0xB3, 0x73, 0xF3,0x0B, 0x8B, 0x4B, 0xCB, 0x2B, 0xAB, 0x6B, 0xEB, 0x1B, 0x9B, 0x5B, 0xDB, 0x3B, 0xBB, 0x7B, 0xFB, 0x07, 0x87, 0x47, 0xC7, 0x27, 0xA7, 0x67, 0xE7, 0x17, 0x97, 0x57, 0xD7, 0x37, 0xB7, 0x77, 0xF7, 0x0F, 0x8F, 0x4F, 0xCF, 0x2F, 0xAF, 0x6F, 0xEF, 0x1F, 0x9F, 0x5F, 0xDF, 0x3F, 0xBF, 0x7F, 0xFF,};unsigned int I, J;unsigned char *Ic = (unsigned char*) &I;unsigned char *Jc = (unsigned char*) &J;for(I = 1; I < N - 1; I++){ Jc[0] = reverse256[Ic[3]]; Jc[1] = reverse256[Ic[2]]; Jc[2] = reverse256[Ic[1]]; Jc[3] = reverse256[Ic[0]]; J >>= (32 - T); if (I < J) { S = x[I]; x[I] = x[J];x[J] = S; }}Напомним основные формулы:
 (16) (16)
На рисунке проиллюстрирован второй этап вычисления ДПФ. Линиями сверху вниз показано использование элементов для вычисления значений новых элментов. Очень удобно то, что два элемента на определенных позициях в массиве дают два элемента на тех же местах. Только принадлежать они будут уже другим, более длинным массивам, размещенным на месте прежних, более коротких. Это позволяет обойтись одним массивом данных для исходных данных, результата и хранения промежуточных результатов для всех T итераций.

рис. 4
Итак, вот действия, которые нужно выполнить после первичной перестановки элементов.
#define T 4#define Nmax (2 << T)complex Q, Temp, j(0,1);static complex x[Nmax];static double pi2 = 2 * 3.1415926535897932384626433832795;int N, Nd2, k, mpNd2, m;for(N = 2, Nd2 = 1; N <= Nmax; Nd2 = N, N += N){ for(k = 0; k < Nd2; k++) { W = exp(-j*pi2*k/N); for(m = k; m < Nmax; m += N) { mpNd2 = m + Nd2; Temp = W * x[mpNd2]; x[mpNd2] = x[m] - Temp;x[m] = x[m] + Temp; } }} Переменная Nmax содержит полную длину массива данных и окончательное количество элементов ДПФ. В таблице показано соответствие между выражениями в формуле (16) и переменными в программе.
| В алгоритме |
В формуле |
| N |
N |
| Nd2 |
N/2 |
| k |
k |
| m |
k с поправкой на номер последовательности |
| mpNd2 |
k+N/2 с поправкой на номер последовательности |
| pi2 |
2π |
| j |
j (мнимая единица) |
| x[k] (в начале цикла) |
X{N/2}[even]k
|
| x[mpNd2] (в начале цикла) |
X{N/2}[odd]k
|
| x[k] (в конце цикла) |
X{N}k
|
| x[mpNd2] (в конце цикла) |
X{N}N/2+k
|
| W |

|
Внешний цикл - это основные итерации. На каждой из них 2Nmax/N ДПФ (длиной по N/2 элементов каждое) преобразуются в Nmax/N ДПФ (длиной по N элементов каждое).
Следующий цикл по k представляет собой цикл синхронного вычисления элементов с индексами k и k + N/2 во всех результирующих ДПФ.
Самый внутренний цикл перебирает Nmax/N штук ДПФ одно за другим.
Именно так, а не иначе: сначала вычисляются элементы с номерами 0 и N/2, во всех ДПФ в количестве Nmax/N штук, потом с номерами 1 и N/2 + 1 и так далее. На рис.4 показана последовательность вычислений для N = 8. Такая последовательность обеспечивает однократное вычисление  . .
Обратите внимание, что x[mpNd2] вычисляется раньше, чем x[k], чтобы значение x[k] не было модифицировано прежде, чем будет использовано.
Алгоритм обратного дискретного преобразования Фурье отличается только тем, что вместо -j надо использовать +j и после всех вычислений поделить каждое x[k] на Nmax.
Для справки: произведение, сумма и экспонента для комплексных чисел вычисляются по формулам:
(x,y)(x',y')=(xx'-yy')(xy'+x'y)
(x,y)+(x',y')=(x+x')(y+y')
e-jv
=(cos v, - sinv)
где v - действительное число.
В приведенной выше программе велико искушение для вычисления поворачивающих множителей использовать формулу:
 . (17) . (17)
Это позволило бы избавиться от возведений в степень и обойтись одними умножениями, если заранее вычислить WN
для N = 2, 4, 8,…, Nmax. Но то, что можно делать в математике, далеко не всегда можно делать в программах. По мере увеличения k поворачивающий множитель будет изменяться, но вместе с тем будет расти погрешность
. Ведь вычисления с плавающей точкой на реальном компьютере совсем без погрешностей невозможны. И после N/2 подряд умножений в поворачивающем множителе может накопиться огромное отклонение от точного значения. Вспомним правило: при умножении величин их относительные погрешности складываются. Так что, если погрешность одного умношения равна s%, то после 1000 умножений она может достигнуть в худшем случае 1000s%.
Этого можно было бы избежать, будь число WN
целым, но оно не целое при N > 2, так как вычисляется через синус и косинус:

Как же избежать множества обращений к весьма медленным функциям синуса и косинуса? Здесь нам приходит на помощь давно известный алгоритм вычисления степени через многократные возведения в квадрат и умножения. Например:

В данном случае нам понадобилось всего 5 умножений (учитывая, что  не нужно вычислять дважды) вместо 13. В худшем случае для возведения в степень от 1 до N/2-1 нужно log2
N умножений вместо N/2, что дает вполне приемлемую погрешность для большинства практических задач.
не нужно вычислять дважды) вместо 13. В худшем случае для возведения в степень от 1 до N/2-1 нужно log2
N умножений вместо N/2, что дает вполне приемлемую погрешность для большинства практических задач.
Можно сократить вдвое количество умножений на каждом шаге, если использовать результаты прошлых вычислений
 , ,
для хранения которых нужно дополнительно log2
(Nmax) комплексных ячеек памяти:

Если очередное  не было вычислено предварительно, то берется двоичное представление k и анализируется. Каждому единичному биту соответствует ровно один множитель. В общем случае единице в бите с номером b (младший бит имеет номер 0) соответствует множитель
не было вычислено предварительно, то берется двоичное представление k и анализируется. Каждому единичному биту соответствует ровно один множитель. В общем случае единице в бите с номером b (младший бит имеет номер 0) соответствует множитель  , который хранится в b-й ячейке упомянутого выше массива.
, который хранится в b-й ячейке упомянутого выше массива.
Есть способ уменьшить количество умножений для вычисления  до одного на два цикла. Но для этого нужно отвести N/2 комплексных ячеек для хранения всех предыдущих
до одного на два цикла. Но для этого нужно отвести N/2 комплексных ячеек для хранения всех предыдущих  . Алгоритм достаточно прост. Нечетные элементы вычисляются по формуле (17). Четные вычисляются по формуле:
. Алгоритм достаточно прост. Нечетные элементы вычисляются по формуле (17). Четные вычисляются по формуле:

То есть, ничего не вычисляется, а берется одно из значений, вычисленных на предыдущем шаге, когда N было вдвое меньше. Чтобы не нужно было копировать величины на новые позиции достаточно их сразу располагать в той позиции, которую они займут при N = Nmax и вводить простую поправку Skew (см. листинг программы).
И последние пояснения относительно листинга.
Во-первых, здесь присутствует реализация простейших операций над комплексными числами (классы Complex и ShortComplex), оптимизированная под данную задачу. Обычно та или иная реализация уже есть для многих компиляторов, так что можно использовать и ее.
Во-вторых, массив W2n содержит заранее вычисленные коэффициенты W2
, W4
, W8
,...,WNmax
.
В-третьих, для вычислений используются наиболее точное представление чисел с плавающей точкой в C++: long double размером в 10 байт на платформе Intel. Для хранения результатов в массивах используется тип double длиной 8 байт. Причина - не в желании сэкономить 20% памяти, а в том, что 64-битные и 32-битные процессоры лучше работают с выровненными по границе 8 байт данными, чем с выровненными по границе 10 байт.
Для чего нужно быстрое преобразование Фурье или вообще дискретное преобразование Фурье (ДПФ)? Давайте попробуем разобраться.
Пусть у нас есть функция синуса x = sin(t).

Максимальная амплитуда этого колебания равна 1. Если умножить его на некоторый коэффициент A, то получим тот же график, растянутый по вертикали в A раз: x = Asin(t).
Период колебания равен 2π. Если мы хотим увеличить период до T, то надо умножить переменную t на коэффициент. Это вызовет растяжение графика по горизонтали: x = A sin(2πt/T).
Частота колебания обратна периоду: ν = 1/T. Также говорят о круговой частоте, которая вычисляется по формуле: ω= 2πν = 2πT. Откуда: x = A sin(ωt).
И, наконец, есть фаза, обозначаемая как φ. Она определяет сдвиг графика колебания влево. В результате сочетания всех этих параметров получается гармоническое колебание
или просто гармоника
:

Очень похоже выглядит и выражение гармоники через косинус:

Большой разницы нет. Достаточно изменить фазу на π/2, чтобы перейти от синуса к косинусу и обратно. Далее будем подразумевать под гармоникой функцию косинуса:
x = A cos(2πt/T + φ) = A cos(2πνt + φ) = A cos(ωt + φ) (18)
В природе и технике колебания, описываемые подобной функцией чрезвычайно распространены. Например, маятник, струна, водные и звуковые волны и прочее, и прочее.
Преобразуем (18) по формуле косинуса суммы:
x = A cos φ cos(2πt/T) - A sin φ sin(2πt/T) (19)
Выделим в (19) элементы, независимые от t, и обозначим их как Re и Im:
x = Re cos(2πt/T) - Im sin(2πt / T) (20)
Re = A cos φ, Im = A sin φ
По величинам Re и Im можно однозначно восстановить амплитуду и фазу исходной гармоники:
 и и  (21) (21)
Рассмотрим очень распространенную практическую ситуацию. Пусть у нас есть звуковое или какое-то иное колебание в виде функции x = f(t). Пусть это колебание было записано в виде графика для отрезка времени [0, T]. Для обработки компьютером нужно выполнить дискретизацию
. Отрезок делится на N-1 равных частей, границы частей обозначим tn
= nT/N. Сохраняются N значений функции на границах частей: xn
= f(tn
) = { x0
, x1
, x2
,..., xN
}.

В результате прямого дискретного преобразования Фурье были получены N значений для Xk
:
 (22) (22)
Теперь возьмем обратное преобразование Фурье:
 (23) (23)
Выполним над этой формулой следующие действия: разложим каждое комплексное Xk
на мнимую и действительную составляющие Xk
= Rek
+ j Imk
; разложим экспоненту по формуле Эйлера на синус и косинус действительного аргумента; перемножим; внесем 1/N под знак суммы и перегруппируем элементы в две суммы:
 (24) (24)
Это была цепочка равенств, которая начиналась с действительного числа xn
. В конце получилось две суммы, одна из которых помножена на мнимую единицу j. Сами же суммы состоят из действительных слагаемых. Отсюда следует, что вторая сумма должна быть равна нулю. Отбросим ее и получим:
 (25) (25)
Поскольку при дискретизации мы брали tn
= nT/N и , то можем выполнить замену: n = tn
N/T. Следовательно, в синусе и косинусе вместо 2πkn/N можно написать 2πktn
/T. В результате получим:
 (26) (26)
Сопоставим эту формулу с формулой (20) для гармоники:
x = Re cos(2πt/T) - Im sin(2πt / T) (20)
Слагаемые суммы (26) аналогичны формуле (20), а формула (20) описывает гармоническое колебание. Значит сумма (26) представляет собой сумму из N гармонических колебаний разной частоты, фазы и амплитуды.
Выше объяснялось, каким образом формула вида (20) может быть преобразована в формулу вида (18):
x = A cos(2πt/T + φ) (18)
Выполним такое же преобразование для слагаемых суммы (26), преобразуем их из вида (20) в вид (18). Получим:
 (27) (27)
Далее будем функцию
Gk
(t) = Ak
cos(2πtk/T + φk
) (28)
называть k-й гармоникой
.
Для вычисления Ak
и φk
надо использовать формулу (21). Теперь выпишем в одном месте все формулы, которые связывают амплитуду, фазу, частоту и период каждой из гармоник с коэффициентами Xk
:
 (29) (29)
Итак.
Физический смысл дискретного преобразования Фурье состоит в том, чтобы представить некоторый дискретный сигнал в виде суммы гармоник. Параметры каждой гармоники вычисляются прямым преобразованием, а сумма гармоник - обратным.
Что такое зеркальный эффект.
Предположим, что исходный сигнал состоял из суммы гармоник. fs
(t) = As
cos(2πtms
/ T + φs
). Пусть мы этот сигнал подвергли дискретизации, выполнили над ним прямое и обратное преобразование Фурье. Представили в виде суммы гармоник Gk
(t) = Ak
cos(2πtk / T + φk
), как это описано в предыдущей главе. Спрашивается, эти гармоники Gk
- те же самые, что и исходные гармоники fs
или нет? Оказывается, нет, не те. Но кое-какую информацию об исходных гармониках все же можно попытаться восстановить.
Эта задача имеет практический интерес. Пусть нам дан некий сигнал, который физически получился как сумма гармонических колебаний (или близких к ним). Простейший пример: кто-то сыграл аккорд, аккорд записан как звуковое колебание в виде mp3 или wav-файла; и надо восстановить, из каких нот аккорд состоял. Или другой случай. Во время испытаний самолета возик флаттер (разрушительные нарастающие колебания), самолет разбился, но самописцы в черном ящике записали изменение перегрузки (суммарное механическое колебание). Надо посмотреть, из каких гармоник состояло это колебание. Каждой гармонике соответствует некоторая часть конструкции. В результате можно понять, какие части самолета колебались сильнее всего и вызвали флаттер.
Вернемся к предыдущей ситуации.
Дана функция f(t) на отрезке [0, T].
Выполнена ее дискретизация, для чего отрезок разбит на N равных частей в точках tn
= Tn/N и вычислены значения функции в этих точках: {x} : xn
= f(tn
) = f(Tn/N).
Пусть выполнено прямое дискретное преобразование Фурье (далее - ДПФ) {X} : Xk
= NAk
e jφ
k
, и функция разложена на сумму из N гармоник:
Gk
(t) = Ak
cos(2πtk / T + φk
)
Теперь предположим, что наша исходная функция сама представляла собой такую гармонику:
f(t) = A cos(2πtm / T + φ).
Получится ли в результате ее преобразования последовательность {X}, в которой все элементы равны нулю, кроме элемента Xm
= NAm
e jφ
m
, который дает как раз эту гармонику?
Gm
(t) = Am
cos(2πtm / T + φm
) = f(t), Am
= A, φm
= φ
Как уже говорилось, нет, нас ждет разочарование. Вместо этой одной гармоники мы получим две:
Gm
(t) = (A/2) cos(2πtm / T + φ) = f(t) / 2 = f'(t)
и
GN-m
(t) = (A/2) cos(2πt(N - m) / T - φ) = f''(t)
Как видите у них половинные амплитуды, противоположные фазы, а частоты зеркально симметрично расположены на отрезке [0, N]. Это - тот самый зеркальный эффект.
Неоднозначность представления суммой гармоник.
Преобразуем сумму этих гармоник по формуле суммы косинусов:

Итого:
f'(t) + f''(t) = A cos(πtN / T) cos(2πtm / T - πtN / T + φ) (30)
А нам требовалось:
f(t) = A cos(2πtm / T + φ) (31)
Однако, формулы (30) и (31) дают один и тот же результат в точках tn
= Tn / N. В самом деле, подставим Tn / N вместо t сначала в (30):
f'(t) + f''(t) =
= A cos(πTnN / TN) cos(2πTnm / TN - πTnN / TN + φ) =
= A cos(πn) cos(2πnm / N - πn + φ) = ...
Второй множитель разложим по формуле косинуса разности, отделив πn:
... = A cos(πn) [cos(2πnm / N + φ) cos(πn) +
+ sin(2πnm / N + φ) sin(πn)] = ...
Учитывая, что для целого n выполняется sin(πn) = 0 и cos2
(πn) = 1, получаем:
... = A cos(πn) [cos(2πnm / N + φ) cos(πn)] =
= A cos2
(πn) cos(2πnm / N + φ) = A cos(2πnm / N + φ) (32)
Теперь подставим Tn / N вместо t в (31):
f(t) = A cos(2πtm / T + φ) = A cos(2πTnm / TN + φ) =
= A cos(2πnm / N + φ) (33)
Формулы (32) и (33) совпадают, что и требовалось доказать.
Из этого примера следует важный вывод. Заданная дискретная последовательность {x} может быть разложена в общем случае на разные
суммы гармоник Gk
(t). Даже в элементарном случае, когда исходная функция представляла собой одну гармонику, в результате можно получить две. То есть, разложение дискретной последовательности на гармоники неоднозначно
.
Этим эффектом мы обязаны именно дискретизации. Дело в том, что если вместо ДПФ использовать его непрерывный аналог - разложение в ряд Фурье непрерывной функции или непрерывное преобразование Фурье f(t), то мы получим единственую правильную гармонику Gm
(t) = A cos(2πtm / T + φ) = f(t). Если же мы применяем ДПФ, то получим сумму гармоник, которая только в точках дискретизации совпадает с исходной функцией:

На этом графике для N = 8 и m = 2 синим цветом показана исходная гармоника f(t) и две гармоники, которые получаются в результате преобразвания Фурье: f'(t) зеленым цветом и f''(t) красным. В точках дискретизации, отмеченных вертикальными штрихами, сумма гармоник f'(t) и f''(t) совпадает с гармоникой f(t).
Заметим также, что тот же результат преобразования получился бы, если бы мы в качестве исходной функции f(t) взяли 2f''(t) или f'(t) + f''(t). Это следует из того, что в результате дискретизации была бы получена та же последовательность {x} и результаты ДПФ, естественно, дали бы то же самое.
Итак, мы имеем правило:
Разложение на гармоники, когда исходные данные представлены дискретным набором точек {x} является принципиально неоднозначным. Функции
f(t) = A cos(2πtm / T + φ),
2f''(t) = A cos(2πt(N-m) / T - φ) и
f'(t) + f''(t) = (A/2) cos(2πtm / T + φ) + (A/2) cos(2πt(N-m) / T - φ)
дают после дискретизации одни и те же исходные данные и те же результаты ДПФ.
Доказательство зеркального эффекта.
В начале главы упоминалось о том, что в результате ДПФ гармонической функции на практике получаются две гармоники. Однако этот эмпирический факт не доказывался. Докажем теперь строго, какие гармоники дает произвольная гармоническая функция f(t) = A cos(2πtm / T + φ) при целочисленном m  [0, N[. [0, N[.
Напомним формулу прямого ДПФ:

В данном случае
xn
= f(tn
) = f(Tn / N) = A cos(2πTnm / NT + φ) = A cos(2πnm / N + φ)
Введем обозначения:
wn
= 2πn / N
Zk,n
= (f(tn
) / A) e-j2πkn / N
= cos(wn
m + φ) e-jw
n
k
В результате формула прямого ДПФ упрощается до:
Xk
= A Zk,n Zk,n
Теперь преобразуем Zk,n
:
Zk,n
= cos(wn
m + φ) e-jw
n
k
=
применяем формулу Эйлера:
= cos(wn
m + φ) (cos(-wn
k) + j sin(-wn
k)) =
= cos(wn
m + φ) (cos(wn
k) - j sin(wn
k)) =
раскрываем скобки:
= cos(wn
m + φ) cos(wn
k) - j cos(wn
m + φ) sin(wn
k) =
применяем формулы произведения косинусов и синуса на косинус:
= (1/2)[cos((wn
m + φ) - wn
k) + cos((wn
m + φ) + wn
k)] -
= - (j/2)[sin(wn
k - (wn
m + φ)) + sin(wn
k + (wn
m + φ))] =
перегруппировываем слагаемые:
= (1/2)[cos((wn
m + φ) - wn
k) + cos((wn
m + φ) + wn
k) -
- j sin(wn
k - (wn
m + φ)) - j sin(wn
k + (wn
m + φ))] =
= (1/2)[cos((wn
m + φ) - wn
k) + cos((wn
m + φ) + wn
k) +
+ j sin((wn
m + φ) - wn
k) - j sin((wn
m + φ) + wn
k)] =
= (1/2)[cos(wn
m + φ - wn
k) + j sin(wn
m + φ - wn
k) +
+ cos(wn
m + φ + wn
k) - j sin(wn
m + φ + wn
k)] =
применяем формулу Эйлера (только наоборот):
= (1/2)[e j(w
n
m + φ - w
n
k)
+ e -j(w
n
m + φ + w
n
k
)] =
и выносим за скобки все, что можно:
= (1/2)[e jφ
e jw
n
(m - k)
+ e -jφ
e -jw
n
(m + k)
]
Теперь подставляем полученные величины в сумму ДПФ и преобразуем:
Xk
= A Zk,n
= Zk,n
=
= A (1/2)[e jφ
e jw
n
(m - k)
+ e -jφ
e -jw
n
(m + k)
] = (1/2)[e jφ
e jw
n
(m - k)
+ e -jφ
e -jw
n
(m + k)
] =
= (A/2)e jφ
 e jw
n
(m - k)
+ (A/2)e -jφ e jw
n
(m - k)
+ (A/2)e -jφ
 e -jw
n
(m + k)
= e -jw
n
(m + k)
=
подставляем wn
:
= (A/2)e jφ
 e j2πn(m - k) / N
+ (A/2)e -jφ e j2πn(m - k) / N
+ (A/2)e -jφ
 e -j2πn(m + k) / N
= e -j2πn(m + k) / N
=
вводим обозначения для сумм:
= (A/2)e jφ
S1
+ (A/2)e -jφ
S2
Легко видеть, что суммы S1
и S2
являются геометрическими прогрессиями, а формула суммы геометрической прогрессии нам известна:
SN
= a0
(qN
- 1) / (q - 1), q ≠ 1 (34)
Первый элемент прогрессии в обоих случаях равен a0
= 1.
Знаменатели прогрессий равны
q1
= e j2π(m - k) / N
для S1
и
q2
= e -j2π(m + k) / N
для S2
.
Условие q ≠ 1 вынуждает нас решить уравнения:
e j2π(m - k) / N
= 1,
и
e -j2π(m + k) / N
= 1,
Учитывая Теорему 0, получим, что условие q ≠ 1 не выполняется при k = m для S1
и при k = (N - m) для S2
.
В случае, когда выполняются оба условия: k = m и k = (N - m), то есть k = m = N /2 обе суммы нельзя считать по формуле геометрической прогресии.
В случае k = m для S1
придется выполнить небольшие дополнительные преобразования:
S1
=  e j2πn(m - m) / N
= e j2πn(m - m) / N
=  1 = N 1 = N
Аналогично в случае k = N - m для S2
:
S2
=  e -j2
π
n(m + N - m) / N
= e -j2
π
n(m + N - m) / N
=  e -j2
π
n
= e -j2
π
n
=  1 = N 1 = N
В случае k = m = N / 2 имеем:
Xk
= (A/2)Ne j
φ
+ (A/2)Ne -j
φ
=
= (A/2)N(e j
φ
+ e -j
φ
) =
= (A/2)N(cos φ + j sin φ + cos φ - j sin φ) =
= (A/2)N(2 cos φ) =
= ANcos φ
В случае k = m = 0 имеем:
Xk
= (A/2)e j
φ
N + (A/2)e -j
φ
N = (A/2)N(e j
φ
+ e -j
φ
) =
= (A/2)N(cos φ + jsin φ + cos φ - jsin φ) = ANcos φ
Наконец, получаем формулу для Xk
:
Для k = m = N / 2 или k = m = 0:
Xk
= ANcos φ
Для k = m ≠ N / 2:
Xk
= (A/2)Ne jφ
+ (A/2)e -jφ
(e -j4πm
- 1) / (e -j4πm / N
- 1)
Для k = (N - m) ≠ N / 2:
Xk
= (A/2)e jφ
(e j4πm
- 1) / (e j4πm / N
- 1) + (A/2)Ne -jφ
Для остальных k:
Xk
= (A/2)e jφ
(e j2π(m - k)
- 1) / (e j2π(m - k) / N
- 1) +
+ (A/2)e -jφ
(e -j2π(m + k)
- 1) / (e -j2π(m + k) / N
- 1) (35)
Заметим, что эта формула получена без использования факта целочисленности m и k.
Теперь учтем целочисленность. Для этого применим Теорему 0 и заменим в формуле (35) экспоненты на 1 везде, где выполняется это условие:
Для k = m = N / 2 или k = m = 0:
Xk
= ANcos φ
Для k = m ≠ N / 2:
Xk
= (A/2)Ne jφ
+ (A/2)e -jφ
(1 - 1) / (e -j4πm / N
- 1)
Для k = (N - m) ≠ N / 2:
Xk
= (A/2)e jφ
(1 - 1) / (e j4πm / N
- 1) + (A/2)Ne -jφ
Для остальных k:
Xk
= (A/2)e jφ
(1 - 1) / (e j2π(m - k) / N
- 1) +
+ (A/2)e -jφ
(1 - 1) / (e -j2π(m + k) / N
- 1)
Сокращаем везде, где получаются нули, и приходим к формулам:
Для k = m = N / 2 или k = m = 0:
Xk
= ANcos φ
Для k = m ≠ N / 2:
Xk
= (A/2)Ne jφ
Для k = (N - m) ≠ N / 2:
Xk
= (A/2)Ne -jφ
Для остальных k:
Xk
= 0 (36)
Вывод:
Зеркальный эффект всегда проявляется так, что гармонические колебания:
f(t) = A cos(2π
tm / T + φ
),
2f
''(t) = A cos(2π
t(N-m) / T - φ
) и
f'(t) + f''(t) = (A/2) cos(2π
tm / T + φ
) + (A/2) cos(2π
t(N-m) / T - φ
)
в процессе дискретного преобразования Фурье представляются как сумма колебаний
f'(t) + f''(t).
При этом все коэффициенты ДПФ равны нулю за исключением
Xm
= (A/2)Ne j
φ
и
XN - m
= (A/2)Ne -j
φ
кроме частных случаев m = N / 2 и m = 0, в которых единственный ненулевой коэффициент:
Xm
= ANcos φ
В этом последнем частном случае зеркальный эффект выглядит несколько иначе: у исходного гармонического колебания теряется фаза и искажается амплитуда. Лишь частота сохраняется прежней.
Исправление зеркального эффекта.
Таким образом зеркальный эффект в подавляющем большинстве случаев искажает исходную картину, поскольку в действительности очень редко на вход подается сумма двух гармонических сигналов f'(t) + f''(t) именно с таким соотношением частот: mν и (N - m)ν. В результате исходный спектр искажается, словно отражаясь в зеркале:

На этом рисунке сверху показан ожидаемый спектр сигнала, полученный с помощью непрерывного преобразования Фурье, а снизу - полученный на компьютере с помощью дискретного преобразования Фурье. Нижний спектр искажен зеркальным эффектом.
Пусть мы обннаружили ненулевой коэффициент Xm
. Выдвинем гипотезу, что этот коэффициент соответствует исходному гармоническому колебанию. Восстановим его амплитуду, фазу и частоту.
Xm
= (A/2)Ne jφ
f(t) = A cos(2πtm / T + φ).
Частота восстанавливается проще всего: ν = m/T, где m - индекс найденного ненулевого элемента Xm
. Амплитуда и фаза восстанавливаются по формуле (29):

Известно свойство преобразований Фурье: они линейны. То есть, чтобы получить преобразование для суммы функций, можно сделать преобразование для каждой функции и потом их сложить. Проще говоря, сложения и вычитание исходной функции соответствует сложению и вычитанию результатов прямого ДПФ, и сложению и вычитанию результатов обратного ДПФ.
Поэтому, не теряя полезной информации, мы можем вычесть из ДПФ коэффициенты, соответствующие найденной гармонике: Xm
= Rem
+ jImm
и XN - m
= Rem
- jImm
. Для этого мы обнуляем Xm
, а над коэффициентом XN - m
выполняем действия:
ReN - m
:= ReN - m
- Rem
ImN - m
:= ImN - m
+ Imm
Полученный ДПФ можно подвергнуть дальнейшему анализу. В результате таких действий будет выделен набор гармоник, причем при таком выборе гармоники низкой частоты считаются более предпочтительными.
Что такое эффект размазывания.
В предыдущей главе мы рассматривали ситуацию, когда период колебания равнялся целому числу m от периода дискретизации 1/T. Теперь рассмотрим ситуацию, когда это не так. Положим, что частота равна не m, а m+q, где 0 < q < 1. Воспользуемся формулой (35). Поскольку первые несколько условий для нецелого m+q не выполняются, то остается последняя, самая сложная формула, помеченная словами "Для остальных k":

Подставим в эту формулу m+q вместо m и выполним упрощения, воспользовавшись формулой (34) и введя обозначение ρ = 2πj.

Итого:
 , ρ = 2πj (37) , ρ = 2πj (37)
Теперь построим график функции, чтобы понять, как она себя ведет. Ниже показана трехмерная поверхность. По горизонтальной оси отложено k, по вертикальной |Xk
| и по оси, уходящей вглубь плоскости, отложено q от 0.01 до 0.99.

Рис. 1.
На рисунке видно два ярко выраженных ребра. Первое из них всегда приходится на k = m и k = m + 1. Второе ребро получается в результате зеркального эффекта. Высота пика наименьшая в окрестности q = 0.5. А наибольшая в окрестности q = 1 и q = 0 - то есть при целочисленном m.
К сожалению, пик не является единственным ненулевым коэффициентом Фурье. Рядом с ним есть множество меньших, но не нулевых величин. Если при целочисленном m можно наблюдать единственную полоску, то при нецелом m + q эта полоска размазывется.

Рис. 2.
На рисунке приведена практическая ситуация. Это - ДПФ для звука, содержащегося в обычном WAV-файле. Черный цвет соответствует |Xk
|, а синий - Arg(Xk
). Исходный сигнал содержал ноту "ля" второй октавы с частотой 440 гц и фазой в 90 градусов. ДПФ было выполнено для N = 1000. Однако частота дискретизации звука в WAV-файле составляла 44100 Гц, так что период дискретизации был равен T = 1000/44100 секунд и m = 440*1000/44100 = 9.97, то есть, не целое. В результате ярко выраженный пик окружают дополнительные ненулевые значения.
На следующем рисунке:

Рис. 3.
показана "хорошая" ситуация, когда частота исходного звука составляла 441 Гц, и m = 441*1000/44100 = 10, то есть целое. Вы видите только один ненулевой отсчет.
Этот эффект будем называть эффектом размазывания. Вы видите, что он определяет погрешность, с которой можно найти период исходного колебания. Погрешность равна 1/T. При достаточно большом отклонении от целого m эффект может быть очень заметен. Например ниже вы видите ДПФ для сигнала, соответствующего ноте "ля-бемоль":

Рис. 4.
Точнее можно попытаться определить параметры m, A и φ численными методами.
Для поиска φ следует учесть, что изменение A не повлияет на комплексную фазу (аргумент) коэффициентов Xk
. В самом деле, мы можем представить коэффициенты в виде:
Xk
= (A/2)Z(m,φ)k
,
где Z(m,φ)k
- комплексное число, не зависящее от действительного числа A, но зависящее от m и φ:
Z(m,φ)k
= 
Также не зависит от A отношение коэффициентов Xk
/Xl
= Z(m,φ)k
/Z(m,φ)l
.
Это значит, что у нас есть две целевые функции, с помощью которых мы можем найти частоту m/T и фазу φ. Возьмем Xk
, максимальное по модулю. Если соседние отсчеты Xk-1
и Xk+1
равны нулю, то у нас нет эффекта размазывания и параметры восстанавливаются так, как описано в предыдущей главе. На самом деле нам придется сравнивать не с нулем, а с некоторым малым числом, поскольку некоторая погрешность при вычислении ДПФ неизбежна.
Теперь, когда мы убедились в наличии эффекта размазывания, попробуем найти m и φ после чего восстановим A по формуле: A = |2Xk
/ Z(m,φ)k
|.
Сначала найдем два максимальных отсчета Xk
и Xk+1
. Теперь мы знаем, что искомое m лежит на интервале (k, k+1).
Для нахождения m и φ нужно численно решить систему уравнений:
|Z(m,φ)k
/Z(m,φ)k+1
| = |Xk
/Xk+1
|
Arg(Z(m,φ)k
) = Arg(Xk
)
Здесь только две неизвестных - m и φ, неизвестная A исключена. Систему можно решить итерационно. Для этого сначала фиксируем φ и подбираем m, которое удовлетворяет первому уравнению системы. Потом - наоборот фиксируем найденное m и подбираем φ, которое удовлетворяет второму уравнению системы. Потом снова возавращаемся к первому уравнения - до тех пор, пока оба уравнения не окажутся сбалансированы с достаточной точностью.
Ранее мы рассмотрели случаи, когда число элементов преобразования равно степени двойки. К сожалению, на данный момент не существует столь же эффективного алгоритма вычисления ДПФ для произвольного N. Однако, существует алгоритм, который значительно лучше "лобового" решения задачи. Он требует, чтобы N было четным. Допустим, что N = M 2T
= M L. Число L - целая степень двойки, числа M и T - положительные целые.
Сложность этого алгоритма равна N2
/ L + Nlog2
L. Как видите, этот алгоритм тем эффективнее, чем больше L, то есть, чем больше число элементов N "похоже" на степень двойки. В худшем случае, когда L = 2, он лишь немногим лучше "лобового" решения, которое имеет сложность N2
.
Тем не менее, на практике нам часто полезен именно описанный алгоритм. Допустим, у нас имеется оцифрованный звуковой сигнал, длиной в 2001 отсчет, и мы хотим узнать его спектр. Если мы применим обычный алгоритм, то нам придется отрезать "лишний" кусок сигнала, размером почти в его половину, уменьшив число отсчетов до 1024. Но в таком случае мы потеряем гармоники, которые, возможно, возникли только ближе к концу сигнала. Другой вариант: дополнить исходный сигнал до 2048 отсчетов - тоже плох. В самом деле: чем его дополнить? Если нулями, то в результате мы приобретем множество лишних гармоник из-за резкого скачка сигнала вниз на 2001-м отсчете. Совершенно неясно, как интерполировать сигнал на дополнительные 47 отсчетов так, чтобы не появились новые, ненужные гармоники (шумы). И только новый алгоритм решает эту проблему. С помощью него мы можем "отрезать" совсем небольшой кусочек, в 1 отсчет, взяв L = 16 и получив ускорение в 16 раз! Либо мы можем пожертвовать кусочком чуть длиннее, взяв L еще больше. Для реальных сигналов невелика вероятность, что на этом маленьком отрезке спектр резко изменится, так что результат получится вполне удовлетворительный.
Теперь рассмотрим сам алгоритм. Его главной частью является уже знакомый нам алгоритм "fft" для N, равного степени двойки. Этот алгоритм лишь немного модифицирован. Из исходной последовательности длиной N выбирается L элементов, начиная от элемента с номером h (0 ≤ h < M) и с шагом M. В результате получается последовательность из L элементов. Так как L у нас - степень двойки, мы можем применить к полученной последовательности обычный алгоритм БПФ. Результаты преобразования записываются в те же ячейки, откуда были взяты. Изменение алгоритма заключается всего лишь в том, что каждый раз вместо g-го элемента берется элемент с номером h + gM, то есть, выполняется замена индексов по формуле:
g → h + gM (38)
Позднее мы еще дополнительно оптимизируем этот алгоритм, а пока выпишем его результат в виде формулы:
 (39) (39)
Где g = 0, 1,..., L - 1. Как видите, по сравнению с формулой (1) мы выполнили замену переменных: k → g, n → l, N → L и сделали преобразование индексов по формуле (38).
На первом этапе модифицированный алгоритм БПФ применяется ко всем элементам исходной последовательности. Для этого вычисление по формуле (38) выполняется для h = 0, 1,..., M - 1. Каждое такое вычисление меняет L элементов с индексами h, h + M, h + 2M,..., h + (L - 1)M. Таким образом, вызвав M раз этот алгоритм, мы изменим все N = ML элементов заданной последовательности:
На втором этапе заводится новый массив размером в N элементов, и к нему применяется формула:
 (40) (40)
В двойном цикле величина s проходит значения 0..M - 1, а величина r проходит значения 0..L - 1. Общее число итераций, таким образом, равно ML = N. Каждая итерация требует суммирования M элементов. То есть, общее количество слагаемых равно NM. На предварительном этапе мы M раз применили обычный алгоритм БПФ для L элементов, который, как мы уже знаем, имеет сложность L log2
L. Таким образом, общая сложность алгоритма равна:
NM + L log2
L = N(N/L) + ML log2
L = N2
/L + N log2
L.
Тем самым, мы доказали формулу сложности, приведенную в начале главы.
Теперь нам осталось доказать только то, что формула (40) действительно дает ДПФ. Для этого подставим формулу (39) в формулу (40):

... поскольку выражение  не зависит от l, то мы его можем внести под знак внутренней суммы:
не зависит от l, то мы его можем внести под знак внутренней суммы:

... теперь учтем, что L = N/M, чтобы привести выражение в показателе степени к общему знаменателю и упростить:

... теперь воспользуемся Теоремой 0, чтобы добавить полезный множитель, равный единице:

... теперь воспользуемся равенством N = ML, чтобы разбить сумму в числителе на множители:

... теперь выполним замену переменных r + sL → k, m + lM → n:

Эта сумма эквивалентна сумме (1), с точностью до перемены мест слагаемых. В самом деле, если n = m + lM, m = 0..M - 1, l = 0..L - 1, N = LM, то переменная n по мере суммирования принимает все значения от 0 до N - 1 ровно по одному разу. Что и требовалось доказать.
Настало время написать и оптимизировать алгоритм. Посмотрите на исходный алгоритм "fft" и на алгоритм для случая четного N "fft2".
Здесь мы рассмотрим листинг "fft2" сверху вниз, комментируя все детали.
Сверху вы видите фрагмент, совпадающий со старым листингом вплоть до #define M_2PI. Этот макрос определяет константу 2π.
Функция complex_mul выполняет умножение комплексных чисел z1 и z2 и записывает результат в ячейку z.
Мы собираемся вызывать алгоритм "fft" M раз для одного и того же числа элементов L. Для оптимизации мы должны вынести за пределы алгоритма "fft" те действия, которые не зависят от выбора конкретных элементов в массиве.
К таким действиям можно отнести выделение памяти для хранения поворачивающих множителей и освобождение ее. Деление результата на N также можно выполнить позже для всего массива сразу. А главное, мы можем всего лишь однажды вычислить все поворачивающие множители. Для решения этой задачи мы напишем отдельную функцию createWstore, которая и вычисляет множители, и выделает массив ячеек памяти для них. Позднее этот массив будет передаваться как параметр в новый вариант алгоритма "fft".
Функция createWstore представляет собой ту часть основного цикла "fft", которая отвечала за рассчет поворачивающих множителей. Однако, она оптимизирована. Число итераций меньше, чем в исходном алгоритме, поскольку не на всех итерациях выполнялось вычисление нового множителя, иногда происходило только копирование. Поэтому шаг приращений индекса в массиве вдвое больше: Skew2 вместо Skew. Переменная k для определения четности/нечетности нам больше не нужна, так что внутренний цикл останавливается при достижении границы массива WstoreEnd.
Порядок вычисления множителей  будет понятнее на примере. Если L = 32, то порядок изменения k такой (точкой с запятой разделены итерации внешнего цикла, а запятой - внутреннего):
будет понятнее на примере. Если L = 32, то порядок изменения k такой (точкой с запятой разделены итерации внешнего цикла, а запятой - внутреннего):
k = 0; 16; 8, 24; 4, 12, 20, 28; 2, 6, 10, 14, 18, 22, 26; 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23...31
Далее, вместо старого алгоритма "fft" мы напишем новый - "fft_step" с учетом того, что поворачивающие множители считать не надо, и не надо делить результат на N.
Сам алгоритм практически не изменился за исключением того, что все расстояния между элементами массива увеличились в M раз, согласно формуле (38). Приставка "M" перед именами новых переменных означает умножение на M.
На вход этой функции будет передаваться массив со смещением. Тем самым происходит коррекция индекса на +h элементов, согласно формуле (38).
В основной функции сначала анализируется параметр N. Если он нечетный, то мы вынуждены отсечь один элемент (последний) и уменьшить N на единицу. Таким образом, на входе алгоритма требуется N ≥ 2.
Далее вычисляется L как максимальная степень двойки, кратная N, сама эта степень T и величина M.
Затем вычисляются поворачивающие множители для "fft_step" и вызывается сам "fft_step" нужное число раз. Если оказывается, что N является степенью двойки, то сработает обычный "fft".
Следующим шагом мы вычисляем поворачивающие коэффициенты уже для формулы (40). Этот фрагмент алгоритма очень похож на createWstore, поэтому в дополнительных комментариях не нуждается. Результат оказывается в массиве mult.
Далее вычисляется формула (40). Смысл переменных: pX - указатель на Xr+sL
; rpsL = r + sL; mprM = m + rM; one - очередное слагаемое суммы (40).
Величина widx равна остатку от деления m(r + sL) на N. Таким способом мы избегаем выхода за границы массива mult. Это можно делать, благодаря Теореме 1 - ведь поворачивающие множители как раз имеют период N.
Еще можно заметить, что в сумме (40) в первом множителе поворачивающий коэффициент всегда равен 1, благодаря чему мы экономим несколько умножений.
И наконец, происходит корректировка результатов для обратного ДПФ делением на N.
Функция БПФ для четного N называется "fft2".
Пусть N = PQ. Этот представляет собой более общий случай, чем рассмотренный в предыдущей главе. Теперь не требуется, чтобы P или Q были степенями двойки.
Напомним основную формулу:
 (1). (1).
Рассмотрим формулу:
 (41). (41).
Эта формула эквивалентна формуле (1). В самом деле:

Двойная сумма по pQ + q - это все равно, что одинарная сумма по n, просто порядок слагаемых другой.
Вернемся к формуле (41). В скобках там стоит обычное прямое БПФ, только не для всех xn
, а для последовательности из P штук, взятых с шагом Q. Количество последовательностей равно Q. Элементы последовательности выбираются формулой xpQ + q
, где p - номер элемента, q - номер последовательности.
Пусть мы умеем вычислять БПФ для P элементов за время Z(P). Нам понадобится вычислить Q таких БПФ, на что потратим время O(QZ(P)). Тем самым мы получим все множители в скобках из формулы (41). После этого надо будет вычислить N элементов Xk
, каждый из которых потребует O(Q) действий, итого потребуется еще O(NQ) действий, а в сумме - O(QZ(P) + QN) действий.
В предыдущем алгоритме P - было степенью двойки, а для такого числа элементов мы умеем вычислять БПФ за O(Plog2
P) шагов, т.е. Z(P) = Plog2
P, и получится O(QZ(P) + QN) = O(QPlog2
P + QN) = O(Nlog2
P + N2
/P) действий. Тем самым, мы несколько более простым путем получим ту же оценку сложности алгоритма.
Если P - не степень двойки, мы умеем вычислять ПФ за O(P2
) шагов, т.е. Z(P) = P2
, и получится O(QZ(P) + QN) = O(QP2
+ QN) = O(N2
/Q + N2
/P) действий. Если P и Q достаточно велики, это лучше, чем O(N2
).
В "Википедии" нашелся алгоритм сложности O(Nlog2
N)для произвольного N. Алгоритм основан на значительном увеличении числа элементов последовательности и дополнении ее нулями. Хотя такое расширение, естественно, будет компенсироваться высокой скоростью алгоритма.
Длина последовательности берется равной N', где N' - степень двойки ближайшая сверху к 2N. То есть, 4N > N' = 2T
≥ 2N. Т.е. число элементов новой последовательности в худшем случае может превышать число элементов исходной последовательности почти в 4 раза. Например, если N = 9, то N' = 32.
Обозначим

Представим формулу (1) в виде:

Преобразуем степень:
kn = 2kn/2 = (−k2
+ k2
+ 2kn + n2
− n2
)/2 = (−k2
+ (k + n)2
− n2
)/2
Это используем для дальнейшего преобразования формулы (1):

Далее введем обозначения:
x'n
= xn
W −n2/2
X'k
= Xk
W k2/2
Для n > N, полагаем xn
= 0.
Тогда
 (42) (42)
И далее авторы алгоритма выполняют виртуозный "финт ушами". Пусть:
zk
= (2N − 2 − k)
wn
= W z
n
2/2
И превращают формулу (42) в:
 (43) (43)
Проверим:
wzk − n
= W (z
zk − n
)2/2
= W (2N − 2 − (z
k
− n))2/2
= W (2N − 2 − z
k
+ n)2/2
= W (2N − 2 − (2N − 2 − k) + n)2/2
= W (2N − 2 − 2N + 2 + k + n)2/2
= W (k + n)2/2
Правая часть формулы (43) является дискретной сверткой. В общем случае формула свертки имеет вид:
 (44) (44)
где f и g - функции от целых переменных (т.е. дискретные функции). В данном случае роль таких функций играют x'n
и wn
, которые "зависят" от своих индексов как от целых переменных. Свертка обладает замечательным свойством:
F(f * g) = F(f) F(g) (45)
где F(f) - это дискретная функция, которая получается из дискретной функции f с помощью быстрого преобразования Фурье.
Дальнейший порядок вычисления таков. Сначала надо вычислить F(x'), то есть взять набор x'n
и вычислить БПФ для n = 0...N' − 1. Затем вычислить F(w), для чего взять набор wn
и вычислить БПФ для n = 0...N' − 1. Потом по формуле (45) простым перемножением получаем F(x' * w) = F(x') F(w). Просто берем i-й элемент, полученный после БПФ набора x'n
, и умножаем на i-й элемент, полученный после БПФ набора wn
. В результате получим БПФ свертки x' * w. Теперь у нас есть БПФ свертки, из него надо получить саму свертку. Для этого применяем обратное преобразование Фурье. Теперь нам надо найти X'k
. Для этого используем формулу (43). k-й элемент набора Xk
будет соответствовать zk
-му элементу свертки. Наконец, останется перейти от X'k
к Xk
.
В процессе вычислений мы применяли алгоритмы порядка сложности N, N' и N'log2
N' (когда делали три БПФ). Поскольку N' не может превышать N более, чем в 4 раза, то весь алгоритм имеет сложность O(Nlog2
N)
Обратное преобразование требует величины W без минуса в показателе и в конце алгоритма - деления всех полученных элементов на N. Три алгоритма БПФ остаются в этом случае теми же: два прямых перобразования и одно обратное.
На следующей страничке приведен листинг программы, выполняющей прямое и обратное преобразования по этому алгоритму. Оптимизация выполнена примерно теми же способами, что и в предыдущем случае с незначительными модификациями. Переменные x' в алгоритме обозначаются как x_, 2N как N2, N' как N_, zk
как N22, π/N (или −π/N при обратном преобразовании) как piN.
|