МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(государственный технический университет)
ФИЛИАЛ «ВЗЛЕТ»
Кафедра РЭВС
РАЛДЫГИН И.К.
КОНСПЕКТ ЛЕКЦИЙ ПО КУРСУ
«Основы теории цепей». Часть 3.
Переходные процессы в линейных электрических цепях
Учебное пособие для студентов радиотехнической специальности.
ОДОБРЕНО
НА ЗАСЕДАНИИ КАФЕДРЫ РЭВС
«____» ________________ 2004 года
Протокол № ____
|
|
Ахтубинск – 2004
Предисловие к 3-ей части
В третьей части конспекта по Основам теории цепей (ОТЦ) кратко изложены два метода расчета переходных процессов в линейных электрических цепях: Классический метод и Операторный метод. И классический и операторный методы расчета теоретически можно применять для решения задач любой сложности. Каким из них пользоваться определяется автором.
Однако классический метод физически более прозрачен, чем операторный, в котором решение уравнений во многом формализовано. Операторный метод имеет перед классическим явное преимущество если для расчета переходных процессов использовать прикладную программу Mathcad
2000
, особенно в тех случаях, когда воздействующее напряжение является линейно возрастающее или в виде всплеска одной или несколько экспонент.
Глава 1. Основные сведения о переходных процессах в линейных электрических цепях
1.1 Возникновение и общая характеристика переходных процессов
Выше рассматривались цепи, в которых выполнялись два условия: 1) Источники энергии были подключены к цепи теоретически бесконечно давно; 2) Никаких изменений в состоянии цепи не производилось. Такой режим работы цепи называется установившимся или принужденным.
Переходным называют электромагнитный процесс, возникающий в электрической цепи, при переходе от одного установившегося режима к другому. Этот переход может происходить вследствие преднамеренного или случайного отключения цепи, а также подключения ее под напряжение, вследствие обрыва или короткого замыкания в цепи.
Любые изменения в цепи можно представить в виде переключений, которые называются коммутацией. Коммутация на схемах обозначается в виде ключа со стрелкой, обозначающей замыкание или размыкание:
Теоретически считается, что коммутация производится мгновенно.
Установившийся режим работы цепи при заданных и неизменных ее параметрах полностью определяется источником энергии: постоянный ток, переменный ток.
После коммутации, т.е. во время переходного процесса, токи и напряжения в цепи определяются не только внешними, но и внутренними источниками энергии, в качестве которых выступают индуктивности и емкости.
Дело в том, что в режиме, который существовал до коммутации, в катушках и конденсаторах было накоплено определенное количество энергии:
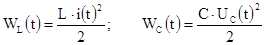
В момент коммутации (t=0) начинается перераспределение энергии между внутренними накопителями и внешними источниками; при этом часть энергии необратимо преобразуется в тепло.
По истечении какого-то времени после коммутации в цепи установится новый режим, который будет обусловлен только внешними источниками энергии. При отключении цепи от внешних источников переходной процесс будет существовать только за счет энергии накопленной в индуктивностях и емкостях, т.е. только за счет внутренней энергии. Новый установившийся режим, в этом случае, будет характеризоваться отсутствием тока в цепи.
Задача анализа переходного процесса заключается в том, чтобы установить по какому закону и как долго будет происходить переход от одного режима к другому.
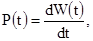 В соответствии с законом непрерывности энергии напряжение на емкости и ток через индуктивность не могут изменяться скачком, т.к. в этом случае мощность, равная скорости изменения энергии обращалась бы в бесконечность, что физически невозможно. В соответствии с законом непрерывности энергии напряжение на емкости и ток через индуктивность не могут изменяться скачком, т.к. в этом случае мощность, равная скорости изменения энергии обращалась бы в бесконечность, что физически невозможно.
На основании изложенного сформулированы два закона коммутации:
· Заряд и напряжение на емкости в момент коммутации остаются такими же, какими они были непосредственно перед коммутацией, а затем плавно изменяются;
· Ток через индуктивность в момент коммутации остается таким же, каким он был непосредственно перед коммуникацией, а затем плавно изменяется.
Математически законы коммутации записываются в следующем виде:
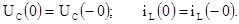
Ток через емкость и напряжение на индуктивности могут изменяться скачком.
1.2 Начальные условия
Значения токов, напряжений и их производных в момент коммутации называют начальными условиями.
Начальные условия подразделяются на зависимые и независимые.
Напряжение на емкости и ток через индуктивность, непосредственно перед коммутацией, называются независимыми начальными условиями, т.к. их значения не зависят от вида и места коммутации и определяются только энергетическим состоянием цепи непосредственно перед коммутацией.
Зависимыми начальными условиями являются токи через емкость и напряжение на индуктивности в момент коммутации. Они зависит от вида и места коммутации и в общем случае, в момент коммутации, могут изменяться скачком.
Независимые начальные условия определяются в цепи до коммутации, а зависимые начальные условия определяются в цепи образовавшейся в момент коммутации.
1.3 Математические основы анализа переходных процессов
Электромагнитные процессы в линейных электрических цепях в установившемся режиме описываются законами Кирхгофа для мгновенных или комплексных значений токов и напряжений.
Для определения законов изменения токов и напряжений в переходном режиме необходимо линейные уравнения, составленные по законам Кирхгофа для мгновенных значений, записать в виде дифференциальных уравнений, а затем решить эти уравнения относительно искомых токов и напряжений.
Таким образом, анализ переходных процессов сводится к решению обыкновенных дифференциальных уравнений с правой частью.
На практике для решения дифференциальных уравнений применяют классический и операторный методы расчета.
Суть классического метода расчета рассмотрим на конкретном примере.
Пусть задана электрическая цепь из последовательно соединенных RC элементов Рис.1.1.
 Рис. 1.1. Цепь RC в момент t=0 при нулевых начальных условиях, Uc
(0)=0, подключается к источнику постоянного напряжения Рис. 1.1. Цепь RC в момент t=0 при нулевых начальных условиях, Uc
(0)=0, подключается к источнику постоянного напряжения
Определим, в общем виде, законы изменения напряжения на емкости и ток в цепи после коммутации.
Решение.
При анализе переходных процессов классическим методом необходимо составить уравнения по законам Кирхгофа для мгновенных значений токов и напряжений. В данном случае можно составить только одно уравнение по второму закону Кирхгофа:
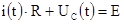 (1.1) (1.1)
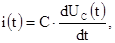
Поскольку исходное алгебраическое уравнение (1.1) можно записать в дифференциальной форме:
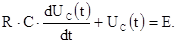
(1.2)
При анализе переходных процессов в качестве искомых функций могут выступать токи и напряжения на пассивных элементах цепи, образовавшейся после коммутации. Для общности обозначений, принятых в математике, условимся в дальнейшем искомую функцию обозначать Y
(
t
)
.
Тогда дифференциальное уравнение (1.2) можно записать в виде:
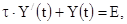 (1.3) (1.3)
где 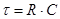 - постоянная времени. - постоянная времени.
Из курса математики известно, что полное решение дифференциального уравнения (1.3) представляется в виде суммы двух составляющих:
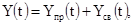
(1.4)
где Y
пр
(
t
)
- принужденная составляющая;
Y
св
(
t
)
- свободная составляющая.
Принужденная составляющая искомого тока или напряжения определяется из анализа установившегося режима в цепи, образовавшейся после коммутации, для чего применяются любые известные методы расчета: по законам Кирхгофа, методом контурных токов и др.
Таким образом, принужденная составляющая зависит от вида источника напряжения и параметров цепи, образовавшейся после коммутации.
Свободная составляющая искомого тока или напряжения представляет собой решение уравнения (1.3) без правой части:
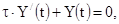
(1.5)
а именно:
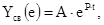
(1.6)
где 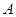 - постоянная интегрирования, которая зависит от начальных условий; - постоянная интегрирования, которая зависит от начальных условий;
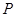 - корень характеристического уравнения - корень характеристического уравнения
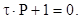 (1.7) (1.7)
Свободная составляющая является результатом действия внутренних источников энергии, когда они не уравновешены внешними источниками. Свободная составляющая с течением времени затухает и в пределе стремится к нулю.
Свободная составляющая не зависит от вида воздействующих внешних источников энергии, и ее характер определяется только свойствами цепи, образовавшейся после коммутации.
Таким образом, закон изменения искомого тока или напряжения в переходном режиме определяется двумя факторами: свойствами цепи образовавшейся после коммутации и приложенным напряжением.
Глава 2. Переходные процессы в цепях первого порядка
2.1 Общий алгоритм расчета переходных процессов в цепях первого порядка классическим методом
Электрической цепью первого порядка называется цепь, которая включает в себя только один накопитель энергии (индуктивности или емкость) или сколько угодно накопителей одного характера, но которые могут быть заменены одним эквивалентным.
На основании вышеизложенного составлен алгоритм расчета переходных процессов в цепях первого порядка, который сводится к выполнению следующих операций.
1. Расчет независимых начальных условий производится в цепи непосредственно перед коммутацией, в результате чего определяются значения напряжений на емкости и ток через индуктивность в момент коммутации:
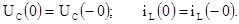
Независимые начальные условия бывают нулевые, когда UC
(0) = 0,
iL
(0) = 0
и ненулевые, когда UC
(0)
¹ 0,
iL
(0)
¹ 0
.
2. Расчет зависимых начальных условий производится в цепи, которая образовалась после коммутации. Для этого необходимо составить уравнения по законам Кирхгофа и рассмотреть их на момент коммутации t
=0
. После этого определяются зависимые начальные условия, например, для цепи Рис.1.1:
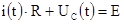
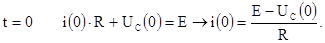
3. Расчет принужденных составляющих производится в цепи, которая образовалась после коммутации, используя известные методы расчета установившихся процессов. В результате определяются принужденные составляющие искомых токов и напряжений Y
пр
(
t
)
.
Например, для цепи Рис.1.1:
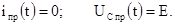
4. Составление характеристического уравнения и определение его корня. Для решения дифференциального уравнения первого порядка, например (1.5), необходимо составить характеристическое уравнение первого порядка и найти его корень.
Характеристическое уравнение можно составить двумя способами, например, для цепи Рис.1.1:
· либо путем формальной замены оператора дифференцирования оператором 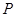
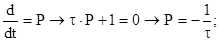
· либо для цепи, образовавшейся после коммутации, составить комплексное входное сопротивление, а затем путем формальной замены j
*
w
=
P
получить операторное сопротивление, которое приравнять к нулю и найти корень этого уравнения.
Например, для цепи Рис.1.1:
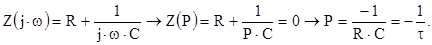
5. Определение свободных составляющих искомых токов и напряжений.
Свободные составляющие всех токов и напряжение в цепях первого порядка представляют собой решение дифференциального уравнения без правой части (1.5) и записываются в виде:
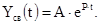
(2.1)
Например, для цепи Рис.1.1 свободные составляющие для тока в цепи и напряжения на емкости имеют вид:
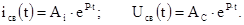
Они отличаются друг от друга только постоянными интегрирования.
6. Расчет постоянных интегрирования. Для расчета постоянных интегрирования, входящих в (2.1), необходимо составить полное решение дифференциального уравнения и рассмотреть его на момент коммутации 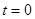 : :
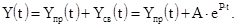 (2.2) (2.2)
При t
=0
имеем:
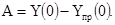 (2.3) (2.3)
Например, для цепи Рис.1.1:
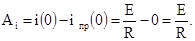 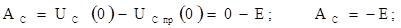
7. Запись полного решения дифференциального уравнения (2.3):
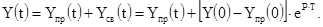
Для цепи Рис.1.1 получим:
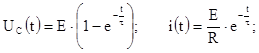 (2.4) (2.4)
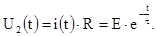
2.2 Переходные процессы в цепи
RC
при подключении ее к источнику постоянного напряжения и коротком замыкании
Рассмотрим электрическую цепи, изображенную на Рис.2.1, которая в момент 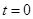 , при нулевых начальных условиях UC
(0)=0
, подключается к источнику постоянного напряжения E
, а затем в момент t
1
>
0
в цепи происходит короткое замыкание, (ключ K
2
замыкается, а ключ K
1
размыкается). , при нулевых начальных условиях UC
(0)=0
, подключается к источнику постоянного напряжения E
, а затем в момент t
1
>
0
в цепи происходит короткое замыкание, (ключ K
2
замыкается, а ключ K
1
размыкается).
  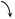     Рис. 2.1. Цепь RC при подключении к источнику постоянного напряжения (ключ 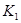 замыкается, ключ замыкается, ключ 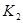 - разомкнут) и коротком замыкании (ключ - разомкнут) и коротком замыкании (ключ 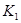 - размыкается, а ключ - размыкается, а ключ 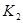 - замыкается). - замыкается).
Определим законы изменения напряжений на емкости и на резисторе после первой и второй коммутаций.
Законы изменения напряжений на емкости и резисторе после первой коммутации получены при изложении алгоритма расчета переходных процессов в цепях первого порядка (2.4).
Определим теперь эти законы после второй коммутации, полагая, что вторая коммутация произошла в момент t
>
0
.
Фактически требуется рассчитать переходные процессы в цепи RC при ненулевых начальных условиях.
Следуя принятому алгоритму, получим следующее:
1. Независимые начальные условия. Напряжение на емкости в момент t
1
будет:
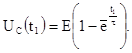
2. Зависимые начальные условия определим из уравнения, составленного по второму закону Кирхгофа, для цепи образовавшейся после второй коммутации:
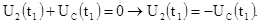
3. Принужденные составляющие после второй коммутации будут равны нулю, т.к. в цепи нет источника напряжения:
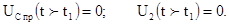
4. Характеристическое уравнение остается таким же как после первой коммутации:
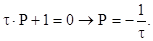
5. Свободные составляющие не зависят от входного напряжения, поэтому определяются по формуле (2.1).
6. Постоянные интегрирования определяются по формуле (2.3).
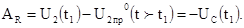 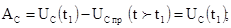
7. Законы изменения напряжений на емкости и на резисторе после второй коммутации принимают вид:
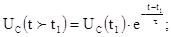
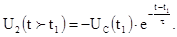
Из формулы (2.4) видно, что нарастание напряжения на емкости происходит тем быстрее, чем меньше постоянная времени. Для различных моментов времени напряжение на емкости, отнесенное к входному напряжению, характеризуется следующими данными (Таблица 2.1).
Таблица 2.1.
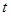
|
0
|
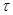
|
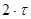
|
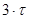
|
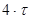
|
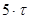
|
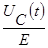
|
0
|
0,63
|
0,86
|
0,95
|
0985
|
0,993
|
Переходной процесс теоретически продолжается бесконечно долго. Однако, как видно из приведенной таблицы, в цепях первого порядка он заканчивается через время, равное (4…
5)*
t
после коммутации. В связи с этим принято считать, что длительность переходного процесса в цепях первого порядка составляет
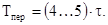 В заключение отметим, что описанные выше переходные процессы возникают при подключении цепи RC к одиночному прямоугольному импульсу напряжением E
и длительностью t
1.
В связи с этим характер изменения напряжений на емкости и резисторе будет определяться соотношением между постоянной времени цепи и длительностью импульса. В заключение отметим, что описанные выше переходные процессы возникают при подключении цепи RC к одиночному прямоугольному импульсу напряжением E
и длительностью t
1.
В связи с этим характер изменения напряжений на емкости и резисторе будет определяться соотношением между постоянной времени цепи и длительностью импульса.
Ниже приведен пример расчета переходных процессов в цепи RC по программе Mathcad (Рис.2.2), а также пример электронного моделирования работы этой цепи по программе Electronics Workbench (Рис.2.3 и Рис.2.4). Из этих рисунков видно, что результаты расчетов и результаты моделирования практически совпадают.

2.3 Переходные процессы в цепи
RC
при подключении ее к источнику синусоидального напряжения
Рассмотрим цепи RC Рис.1.1, которая при нулевых начальных условиях UC
(0)=0
подключается к источнику синусоидального напряжения
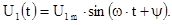
Определим для этой цепи закон изменения напряжения на емкости UC
(
t
)
после коммутации, применив вышеприведенный алгоритм.
1. Независимые начальные условия UC
(0)=0
.
2. Зависимые начальные условия
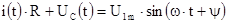
На момент коммутации 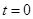 , получим , получим
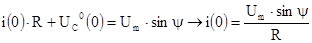
3. Амплитуда принужденной составляющей напряжения на емкости определяется по общему правилу расчета одноконтурных цепей.
Определим модуль входного сопротивления
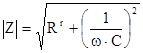
и его аргумент
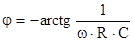
Определяем комплексную амплитуду тока в цепи в установившемся режиме
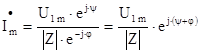
Определим комплексную амплитуду напряжения на емкости
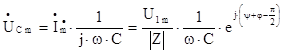
Теперь можно записать принужденную составляющую напряжения на емкости
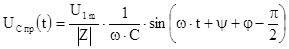
4.5. Характеристическое уравнение и его корень, а также свободная составляющая не зависят от вида входного напряжения и определяются по ранее приведенным формулам
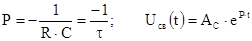
5. Постоянная интегрирования:
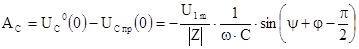
6. Закон изменения напряжения на емкости принимает следующий вид:
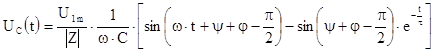
Ниже приведен пример 2.2 расчета переходных процессов в цепи RC при подключении ее к источнику синусоидального напряжения при нулевых начальных условиях Рис.2.5. На Рис.2.6 приведены результаты электронного моделирования этой цепи при синусоидальном воздействии.
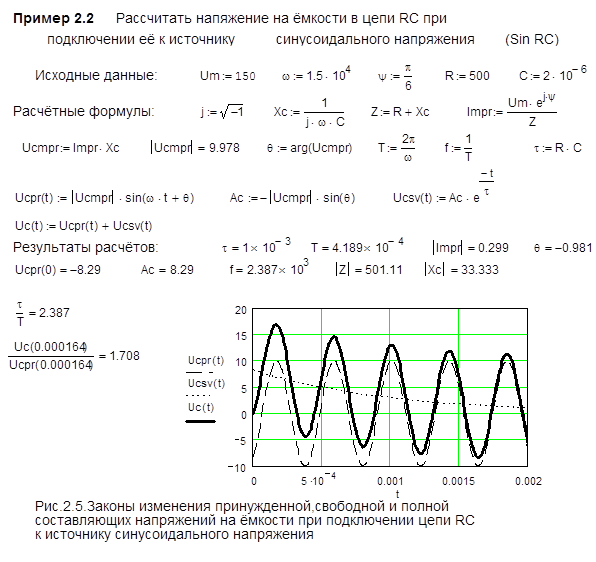
Из этих рисунков видно, что результаты расчетов по программе Mathcad (Рис.2.5) и результаты электронного моделирования по программе Elecrronics Workbench (Рис.2.6) практически совпадают.
В первый полупериод после коммутации напряжение на емкости в 1,7 раза больше принужденной составляющей, что необходимо учитывать при выборе пробивного напряжения на конденсаторе.
2.4 Переходные процессы в цепи
RL
при подключении ее к источнику постоянного напряжения и коротком замыкании
Рассмотрим электрическую цепь, состоящую из последовательно соединенных RL элементов Рис.2.7.
  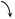    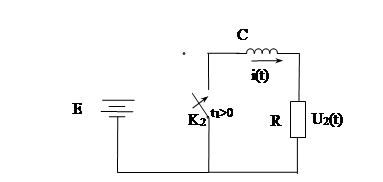 Рис. 2.7. Цепь RL в момент t
=0
при нулевых начальных условиях i
(0)=0
подключается к источнику постоянного напряжения; в момент 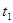 ключ ключ 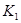 размыкается, а ключ размыкается, а ключ 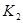 замыкается. замыкается.
Определим законы изменения напряжений на резисторе и индуктивности после первой коммутации и после второй.
Вначале определим U
2
(
t
) ,
UL
(
t
)
после первой коммутации: K
1
- замкнут, K
2
- разомкнут.
1. Независимые начальные условия
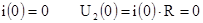
2. Зависимые начальные условия
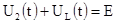
На момент первой коммутации имеем
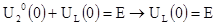
Отсюда следует, что индуктивность в момент коммутации представляет собой разрыв цепи. До коммутации напряжение на индуктивности было равно нулю, а в момент коммутации оно скачком принимает значение, равное входному напряжению.
3. Принужденные составляющие.
В установившемся режиме в цепи будет протекать постоянный ток, при котором индуктивное сопротивление равно нулю и поэтому
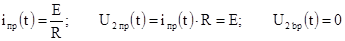
4. Характеристическое уравнение и его корень
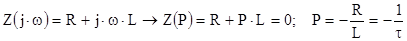
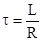
где - постоянная времени цепи RL.
5. Свободные составляющие
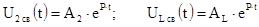
6. Постоянные интегрирования
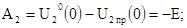
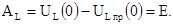
7. Законы изменения напряжений на индуктивности и резисторе после первой коммутации:
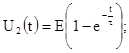
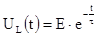
Переходные процессы в цепи RL при коротком замыкании (после второй коммутации).
Переходные процессы в цепи RL Рис.2.7 происходят при ненулевых начальных условиях.
1. Независимые начальные условия на момент t
1
>0
:
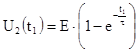
2. Зависимые начальные условия
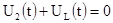
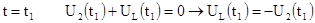
3. Принужденные составляющие.
В цепи после второй коммутации нет источников напряжения, поэтому
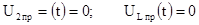
4. Характеристическое уравнение и его корень после второй коммутации такие же, как после первой:
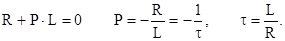
5. Свободные составляющие

6. Постоянные интегрирования
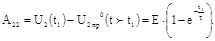
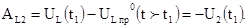
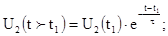 7. Законы изменения напряжений на индуктивности и резисторе после второй коммутации: 7. Законы изменения напряжений на индуктивности и резисторе после второй коммутации:
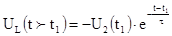
Ниже приведен пример расчета переходных процессов в цепи RL, выполненный по программе Mathcad (Рис.2.8), а также результат электронного моделирования переходных процессов (Рис.2.9), который получен по программе ElectronicsWorkbench (EWB). Из анализа Рис.2.8 и Рис.2.9 видно, что кривые U
2
(
t
)
и UL
(
t
)
первого рисунка практически совпадают с одноименными кривыми второго рисунка.

2.5 Подключение цепи RL к источнику синусоидального напряжения
Пусть цепь RL Рис. 2.7. при нулевых начальных условиях подключается к источнику синусоидального напряжения с начальной фазой не равной нулю:
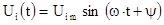
Определим закон изменения тока в цепи после коммутации.
1. Независимые начальные условия i
(0)=0
.
2. Зависимые начальные условия
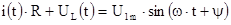
На момент коммутации t
=0
имеем
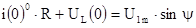
Отсюда получаем:
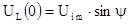
3. Принужденная составляющая тока в цепи:
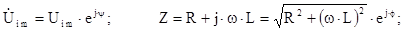
где
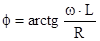 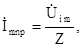
Отсюда амплитуда принужденной составляющей тока
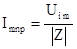
Мгновенное значение принужденной составляющей тока
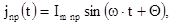
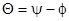
4.5. Характеристическое уравнение и его корень, а также свободная составляющая тока не зависят от вида входного напряжения и определяются по ранее приведенным формулам:
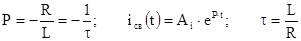
6. Постоянная интегрирования
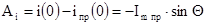
7. Закон изменения тока в цепи RL при подключении ее к источнику синусоидального напряжения

Ниже приведен пример 2.4 расчета переходных процессов в цепи RL при подключении ее к источнику синусоидального напряжения.
Из приведенных формул видно, что при подключении цепи RL к источнику синусоидального напряжения ток в переходном режиме содержит две составляющие: синусоиду и экспоненту и его значение, в первый момент после коммутации, зависит от фазы включения.
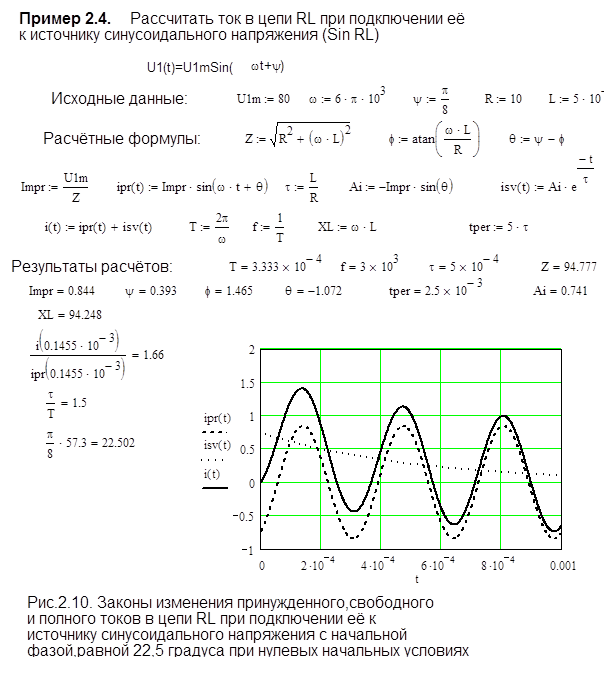
Если включение произошло в момент, когда y
=
f
, то свободная составляющая будет отсутствовать и в цепи сразу будет установившийся режим (удачное включение). Наоборот, неудачное включение имеет место, когда начальная фаза входного напряжения будет y
=
f
±
90
°
.
Если при этом постоянная времени велика, то в начальный момент после коммутации ток переходного режима может достигнуть почти удвоенной амплитуды принужденной составляющей, что наглядно показано на Рис.2.10, где ток переходного режима в 1,66 раза больше амплитуды принужденной составляющей.
2.6 Синтез цепи
RC
с заданными параметрами переходного процесса
Выше рассматривались переходные процессы при заданных параметрах RC-элементов.
На практике возникает необходимость в решении обратной задачи: рассчитать потребные значения RC-элементов, при которых обеспечивалась бы заданная длительность переходного процесса и заданное значение выходного напряжения, снимаемого с резистора.
Рассмотрим электрическую цепь, изображенную на Рис.2.11.
Рис. 2.11. Исходная схема для расчета неизвестных R1
и C
На вход этой цепи подается последовательность однополярных прямоугольных импульсов напряжением E
B
, длительностью ti
, с частотой f
и скважностью 2.
Для синхронного управления ключевыми схемами с помощью цепи Рис.2.11 необходимо сформировать остроконечные импульсы, длительность которых была бы во много раз меньше длительности прямоугольных импульсов на входе цепи. Другими словами, заряд и разряд конденсатора должен происходить за время много меньше, чем длительность прямоугольного импульса
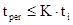
где K
<<1
- коэффициент длительности переходного процесса в цепи Рис.2.11.
При этом заданными величинами должны быть: сопротивление нагрузки R
2
, с которого снимается напряжение и максимальное значение U
2
этого напряжение (U
2
<
E
).
Решение.
Из условия задачи следует, что необходимо определить два параметра:
R
1
- балластное (регулировочное) сопротивление;
C
- емкость конденсатора цепи Рис.2.11.
В соответствии с принятым алгоритмом расчета переходных процессов в цепях первого порядка получаем следующее.
1. Независимые начальные условия:
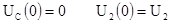
где U
2
- потребное значение напряжения на нагрузке в момент коммутации.
2. Зависимые начальные условия.
К зависимым начальным условиям, в данном случае, относится напряжение на балластном сопротивление 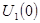 . Для определения этого напряжения составим уравнение по второму закону Кирхгофа и рассмотрим его на момент коммутации (на момент воздействия первого импульса): . Для определения этого напряжения составим уравнение по второму закону Кирхгофа и рассмотрим его на момент коммутации (на момент воздействия первого импульса):
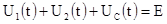
На момент воздействия первого импульса t
=0
имеем
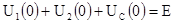
Поскольку UC
(0)=0,
U
2
(0)=
U
2
, следовательно, U
1
(0)
должно быть равным:
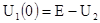
С другой стороны на момент t
=0
можно записать
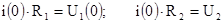
Разделив левые и правые части этих соотношений, получим:
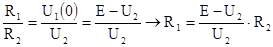
Для определения потребного значения емкости примем во внимание, что длительность переходного процесса в спроектированной цепи должно составлять не более
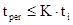
Это означает, что должно выполняться равенство:
5*
t
=K*ti
или 5*(R1
+R2
)*C=K*ti
.
Отсюда получаем потребное значение емкости
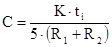
Расчет законов изменения напряжений на емкости и резисторах R
1
,
R
2
в цепи Рис.2.11 можно производить по формулам, приведенным в примере 2.1. Однако, ограничимся расчетом потребных значений R
1
,
C
, но выполним электронное моделирование спроектированной цепи.
Результаты расчетов и электронного моделирования приведены в примере 2.5.
Из Рис.2.12, где приведены результаты электронного моделирования, видно, что для спроектированной цепи RC переходной режим является «штатным». Данную цепь можно рассматривать как генератор остроконечных импульсов или преобразователь напряжения: прямоугольные импульсы преобразуются в остроконечные.
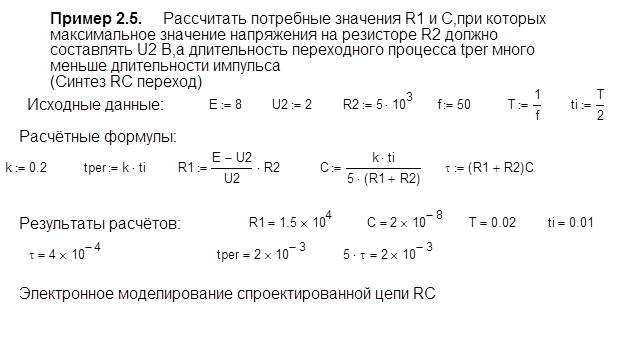
Глава 3. Переходные процессы в цепях второго порядка
3.1 Общая характеристика переходных процессов в цепях второго порядка
Цепями второго порядка называются цепи, в которых содержится два накопителя энергии: индуктивность и емкость.
Электрические цепи второго порядка бывают разветвленными и неразветвленными. К неразветвленным цепям второго порядка относится последовательный колебательный контур. К разветвленным цепям второго порядка относятся Г-образные фильтры нижних и верхних частот.
Электромагнитные процессы в цепях второго порядка описываются дифференциальными уравнениями второго порядка.
Например, дифференциальное уравнение относительно тока в последовательном колебательном контуре можно получить из уравнения, составленного по второму закону Кирхгофа, для мгновенных значений тока и напряжений:
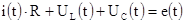
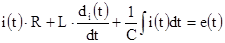
После дифференцирования (3.2) получим дифференциальное уравнение второго порядка относительно тока
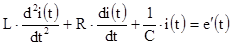
Обозначим, как и ранее, искомый ток i
(
t
)
через Y
и разделим левую и правую части (3.3) на L
, получим дифференциальное уравнение второго порядка:
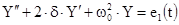
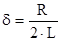
где - коэффициент затухания;
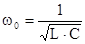
- резонансная частота контура;
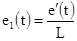
- правая часть дифференциального уравнения (3.3).
Из курса математики известно, что решение дифференциального уравнения второго порядка, также как и первого, представляется в виде двух слагаемых:
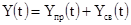
где Y
пр
(
t
)
- принужденная составляющая искомого тока или напряжения, которая зависит от вида источника напряжения, оставшегося в цепи после коммутации;
Y
св
(
t
)
- свободная составляющая, характер которой определяется только структурой цепи образовавшейся после коммутации.
Для решения дифференциального уравнения второго порядка, также как и первого, и по тем же правилам, составляется характеристическое уравнение, которое, в общем, имеет вид:
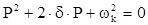
Корни этого уравнения:
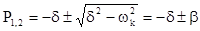
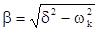 где . где .
Свободная составляющая искомого тока или напряжения записывается в виде:
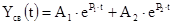 (3.8) (3.8)
где A
1
,
A
2
- неизвестные постоянные интегрирования, которые зависят от начальных условий.
Допустим, что для цепи второго порядка составлено характеристическое уравнение (3.6) и определены его корни (3.7), а также найдены принужденные составляющие искомых токов и напряжений. Тогда общее решение дифференциального уравнения можно записать в виде:
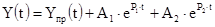 . (3.9) . (3.9)
Для определения двух неизвестных 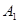 и и 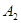 необходимо составить два уравнения. необходимо составить два уравнения.
В качестве первого уравнения используется уравнение (3.9), а в качестве второго – используется первая производная от (3.9).
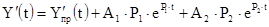
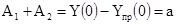 Рассматривая (3.9) и (3.10) на момент t
=0
, получим два уравнения с двумя неизвестными A
1
и A
2
: Рассматривая (3.9) и (3.10) на момент t
=0
, получим два уравнения с двумя неизвестными A
1
и A
2
:
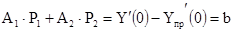
Совместное решение системы (3.11) дает:
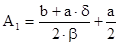
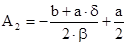
После подстановки корней характеристического уравнения (3.6) и найденных постоянных интегрирования (3.12) в формулу общего решения (3.9) и преобразования, получим закон изменения искомого тока или напряжения:
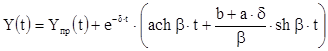
(3.13)
где a
=
Y
(0)-
Y
пр
(0)
; b
=
Y
’(0)-
Y
’пр
(0)
- постоянные коэффициенты, зависящие от начальных условий.
Отметим, что формула (3.13) является общей для всех токов и напряжений в данной цепи второго порядка. При этом меняются только коэффициенты a
и b
и их размерность.
При решении конкретных задач могут представиться три случая.
Случай 1
.
Корни характеристического уравнения (3.7) действительные и разные, что возможно при d>wk
.
В этом случае после коммутации в цепи возникает апериодический режим, при котором все токи и напряжения изменяются плавно, без колебаний, а их законы описываются уравнением (3.13).
Случай 2
.
Корни характеристического уравнения (3.7) действительные и одинаковые, что возможно при d=wk
.
В этом случае в цепи после коммутации возникает критический режим.
При d
=
w
k
,
b
=
Ö
d
2
-
w
k
2
=0,
P
1
=
P
2
=-
d
,
формула (3.13) приобретает другой вид, поскольку

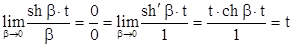
Подстановка полученных результатов в (3.13) дает формулу для расчета законов изменения токов и напряжений в критическом режиме:
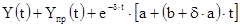
В критическом режиме токи и напряжения, как видно из (3.14), изменяются также плавно, как в апериодическом режиме.
Критический режим лежит на границе между апериодическим и колебательным, к рассмотрению которого приступаем.
Случай 3
.
Корни характеристического уравнения (3.7) комплексные сопряженные, что возможно при d
<
w
k
.
В этом случае в цепи после коммутации возникает колебательный режим.
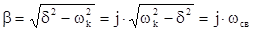 При d
<
w
k
имеем: При d
<
w
k
имеем:
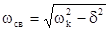
где - частота свободных колебаний.
Корни характеристического уравнения в этом случае принимают вид:
P
1
= -
d
+
j
*
w
св
; P
2
= -
d
-
j
*
w
св
.
Если в формуле (3.13) заменить b = j
*
w
св
, то получим:
 . .
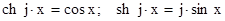
Поскольку, законы изменения токов и напряжений в колебательном режиме принимают вид:
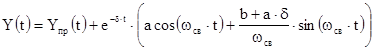
(3.15)
Подчеркнем еще раз, что формулы (3.13), (3.14) и (3.15) являются общими для всех токов и напряжений в цепях второго порядка.
3.2 Алгоритм расчета переходных процессов в цепях второго порядка
На основании вышеизложенного можно предложить следующий алгоритм расчета переходных процессов в цепях второго порядка.
1. Расчет независимых начальных условий производится в цепи до коммутации, в результате чего определяются ток через индуктивность и напряжение на емкости:

2. Расчет зависимых начальных условий производиться для цепи, образовавшейся после коммутации. Для этого составляются уравнения по первому и второму законам Кирхгофа для мгновенных значений токов и напряжений. Затем эти уравнения необходимо рассмотреть на момент t
=0
.
В уравнениях, составленных на момент t
=0
, известными будут: e
(0),
iL
(0)
и UC
(0)
, а неизвестными UL
(0)
и iC
(0)
, которые и определяются.
3. Расчет первых производится на момент t
=0
.
Для определения постоянных коэффициентов a
и b
, входящих в формулы (3.13), (3.14) и (3.15), необходимо знать значения не только искомых функций, но и их первых производных на момент t
=0
.
Первые производные искомых функций определяются путем дифференцирования уравнений, составленных по законам Кирхгофа, и рассмотрения их на момент t
=0
.
При этом в первую очередь определяются первые производные тока через индуктивность и напряжение на емкости, для чего используются уравнения связи между током и напряжением этих элементов.

. (3.16)

После этого определяются первые производные Y
’(0)
.
4. Расчет принужденных составляющих и их первых производных на момент t
=0
.
Принужденные составляющие искомых токов и напряжений определяются любым известным методом расчета установившихся режимов в цепи образовавшейся после коммутации (по законам Кирхгофа, методом контурных токов и др).
Затем полученные выражения для мгновенных значений принужденных токов и напряжений необходимо продифференцировать по времени, после чего определить: Y
пр
(0)
и Y
пр
’(0)
.
5. Расчет постоянных коэффициентов a
и b
.
Постоянные коэффициенты a
и b
определяются по формулам:


6. Составление характеристического уравнения, определение и анализ его корней, выбор расчетной формулы для свободной составляющей.
Одним из описанных выше методов составляется характеристическое уравнение, например, Z
(
P
)=0
и определяются его корни P
1
и P
2
.
На основании анализа корней характеристического уравнения выбирается одна из трех формул (3.13), (3.14), (3.15) для расчета законов изменения тока или напряжения после коммутации.
3.3 Переходные процессы в последовательном колебательном контуре при подключении его к источнику постоянного напряжения
Рассмотрим последовательный колебательный контур (Рис.3.1), который относится к неразветвленным цепям второго порядка.
Пусть данный контур при нулевых начальных условиях подключается к источнику постоянного напряжения 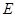 . .

Рис. 3.1. Последовательный колебательный контур
Определим для этих условий законы изменения тока в цепи и напряжений на пассивных элементах после коммутации.
Расчет законов будем вести по принятому выше алгоритму.
1. Независимые начальные условия.
Цепь до коммутации была обесточена, поэтому

2. Зависимые начальные условия.
Зависимым начальным условием, в данном случае, является напряжение на индуктивности. Для его определения составим единственно возможное уравнение по второму закону Кирхгофа для мгновенных значений напряжений и рассмотрим его на момент t
=0
.
 . .
На момент t
=0
получим:

 Поскольку i
(0)=0
и UC
(0)=0
, постольку Поскольку i
(0)=0
и UC
(0)=0
, постольку
Напряжение на индуктивности в момент коммутации скачком принимает значение, равное приложенному напряжению.
3. Первые производные и их значения на момент t
=0
.
В соответствии с (3.16), имеем:

(3.18)
 . .
Производную напряжения на индуктивности найдем после дифференцирования уравнения (3.17) и рассмотрения его на момент t
=0
.

На момент t
=0
, имеем

Таким образом, первые производные для рассматриваемого случая:

4. Принужденные составляющие и их первые производные на момент t
=0
.
В цепи образовавшейся после коммутации (Рис.3.1), через какое-то время конденсатор зарядится до уровня приложенного напряжения 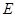 , ток в цепи прекратится, т.к. постоянный ток через емкость не проходит. Принужденные составляющие и их первые производные соответственно будут равны: , ток в цепи прекратится, т.к. постоянный ток через емкость не проходит. Принужденные составляющие и их первые производные соответственно будут равны:


5. Постоянные коэффициенты a
и b
определяются по общей формуле:

.
  
6. Характеристическое уравнение и его корни.
Характеристическое уравнение, соответствующее дифференциальному уравнению второго порядка (3.4), получим из комплексного входного сопротивления цепи Рис.3.1 путем формальной замены j
*
w
®
P
.

Приравняв к нулю Z
(
P
)
и выполнив очевидные преобразования, получим характеристическое уравнение (3.6), корни которого зависят от конкретных значений RLC-элементов рассматриваемого контура Рис.3.1.
 (3.20) (3.20)
В данном случае корни (3.20) определяются по формулам:


где - коэффициент затухания свободной составляющей;

- резонансная частота последовательного контура Рис.3.1;

- постоянная величина.
Как было сказано выше, в цепях второго порядка, в зависимости от вида корней характеристического уравнения (3.19), после коммутации может возникнуть один из трех возможных режимов: апериодический, критический или колебательный.
Найдем закон изменения напряжений на пассивных элементах цепи Рис.3.1 при подключении ее к источнику постоянного напряжения при нулевых начальных условиях для упомянутых случаев.
3.3.1 Апериодический режим
Апериодический режим наступает, если корни характеристического уравнения (3.20) действительные и разные, а это возможно если


где - волновое сопротивление контура;
 - добротность контура. - добротность контура.
Таким образом, в последовательном колебательном контуре (Рис.3.1) апериодический режим наступает при Q
<0.5
.
В связи с этим при анализе переходных процессов в последовательном колебательном контуре отпадает надобность в составлении характеристического уравнения и определении его корней.
В апериодическом режиме законы изменения тока и напряжений на пассивных элементах описываются формулой (3.13).
Если подставить в (3.13) найденные значения коэффициентов a
и b
(см. п.5) и выполнить простейшие преобразования, то получим законы изменения напряжений на пассивных элементах последовательного колебательного контура (3.1) в апериодическом режиме:



Для иллюстрации законов изменения напряжений на пассивных элементах последовательного колебательного контура в апериодическом режиме зададимся произвольными значениями E
,
L
,
C
,
, а сопротивление нагрузки R
выберем таким, чтобы Q
<0.5
и по формулам (3.20) рассчитаем и построим соответствующие графики.
Пример таких расчетов приведен на Рис.3.2.

3.3.2 Критический режим
Критический режим в последовательном колебательном контуре наступает, если корни характеристического уравнения действительные и одинаковые, а это возможно, если:

Таким образом, критический режим в последовательном колебательном контуре наступает при Q<0.5.
Законы изменения напряжений на пассивных элементах цепи Рис.3.1 в критическом режиме описываются формулой (3.14).
 Если подставить в (3.14) значения a
и b
(см. п.5) и выполнить простейшие преобразования, то получим: Если подставить в (3.14) значения a
и b
(см. п.5) и выполнить простейшие преобразования, то получим:
 
Для иллюстрации законов изменения напряжений на пассивных элементах последовательного колебательного контура в критическом режиме выберем значения E
,
L
и C
такими как в примере 3.1, а сопротивление нагрузки выберем из условия Q
=0.5
.
Пример расчетов по формулам (3.21) приведен на Рис.3.3.
Из сравнения рисунков 3.2 и 3.3 следует, что изменения напряжений на резисторе (ток в цепи) в критическом режиме происходят более плавно, чем в апериодическом.
Кроме того, в критическом режиме конденсатор заряжается, примерно, в 2,6 раза быстрее, чем в апериодическом.
Если ограничить длительность переходного процесса в критическом режиме временем t
пер
=5/
d
, при котором UC
(
t
пер
)=0.96*
E
, то возникает возможность синтеза последовательного колебательного контура в заданной длительностью переходного процесса в критическом режиме.
 Пусть задано сопротивление нагрузки R
в цепи рис.3.1, которая подключается к источнику постоянного напряжения при нулевых начальных условиях. Необходимо найти такие значения L
и C
, при которых в цепи возникает критический режим, длительность которого должна составлять t
пер
. Пусть задано сопротивление нагрузки R
в цепи рис.3.1, которая подключается к источнику постоянного напряжения при нулевых начальных условиях. Необходимо найти такие значения L
и C
, при которых в цепи возникает критический режим, длительность которого должна составлять t
пер
.
Решение.
В критическом режиме t
пер
=5/
d
;
 Совместное решение этих уравнений дает формулы для расчета потребных значений индуктивности и емкости Совместное решение этих уравнений дает формулы для расчета потребных значений индуктивности и емкости

3.3.3 Колебательный режим
Колебательный режим в последовательном колебательном контуре возникает, если корни характеристического уравнения комплексные и сопряженные, а это возможно если

В этом случае


где - частота свободных колебаний.
В колебательном режиме законы изменения напряжений на пассивных элементах контура определяются по формуле (3.15).
Подстановка коэффициентов a
и b
(3.19) в формулу (3.15) дает законы изменения напряжений на пассивных элементах контура Рис.3.1:

 . .

Для иллюстрации законов изменения напряжений на пассивных элементах последовательного колебательного контура в колебательном режиме (3.22) выберем значения E
,
L
и C
такими же, как в примерах 3.1 и 3.2, а сопротивление нагрузки выберем из условия Q
=5
.
Пример расчетов по формулам (3.22) приведен на Рис.3.4.
Из анализа изложенного следует, что при Q
>0.5
в последовательном контуре Рис.3.1 возникают затухающие колебания, при которых происходит непрерывный обмен энергией между индуктивностью и емкостью.
Затухание свободных колебаний происходит вследствие необратимых потерь энергии в активном сопротивлении R
.
Длительность переходного процесса в колебательном режиме определятся коэффициентом затухания

Чем больше Q
, т.е. чем меньше R
, тем дольше продолжается переходной процесс.
Частота свободных колебаний всегда меньше резонансной частоты контура

и при

Из Рис.3.4 видно, что напряжение на емкости в начале переходного процесса почти в два раза превышает приложенное напряжение, что необходимо учитывать при выборе пробивного напряжения конденсатора.
Таким образом, режим переходного процесса в колебательном контуре, при подключении его к источнику постоянного напряжения, целиком определяется комбинацией значений RLC-элементов:

При Q
<0.5
- в цепи после коммутации наступает апериодический режим;
при Q
=0.5
- критический режим;
при Q
>0.5
- колебательный режим.

Глава 4. Операторный метод расчета переходных процессов в линейных электрических цепях
4.1 Общие сведения
В предыдущих главах был изложен классический метод расчета переходных процессов в линейных электрических цепях.
Такие процессы описываются линейными дифференциальными уравнениями с постоянными коэффициентами. Для их решения классическим методом необходимо определить постоянные интегрирования, зависящие от начальных условий. По мере усложнения электрических схем и возрастания порядка дифференциальных уравнений трудности, связанные с нахождением постоянных интегрирования, увеличиваются.
Решение упомянутых уравнений может быть выполнено операторным методом, где не требуется дополнительно определить постоянные интегрирования.
При использовании операторного метода действительные функции времени, называемые оригиналами, заменяются их операторными изображениями. В результате чего исходные дифференциальные уравнения заменяются алгебраическими; затем после решения алгебраических уравнений производится обратный переход в область функций действительного переменного.
Связь между оригиналом f
(
t
)
и его изображением устанавливается прямым преобразованием Лапласа:

гдеP
=
s
+
j
*
w
- комплексное число.
Из определения изображения (4.1) следует, что каждый оригинал имеет единственное изображение. В свою очередь, оригинал вполне определяется своим изображением.
 Фразу «оригинал f
(
t
)
имеет своим изображением F
(
P
)
» принято записывать в виде знака соответствия : Фразу «оригинал f
(
t
)
имеет своим изображением F
(
P
)
» принято записывать в виде знака соответствия :
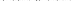
 или или
Существует обратное функциональное преобразование, дающее возможность определить оригинал по его изображению (4.1):
Формула (4.2) называется обратным преобразование Лапласа.

4.2 Изображения простейших функций
При исследовании переходных процессов в электрических цепях чаще всего возникает необходимость в определении изображений единичной функции l
(
t
)
, линейной функции a
*
t
, экспоненциальной функции 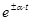 , синусоидальной и косинусоидальной функции, их производных и интегралов. , синусоидальной и косинусоидальной функции, их производных и интегралов.
Единичная функция задается условием:

Изображение единичной функции:

Изображение постоянной величины E
:

Изображение линейной функции:

Изображение экспоненты:

Изображения тригонометрических функций:

Изображение производной от функции f
(
t
)
:

Изображение интеграла от функции f
(
t
)
:

Операция дифференцирования оригинала заменяется операцией умножения на P
изображения, а операция интегрирования оригинала заменяется операцией деления изображения на P
.
4.3 Операторное сопротивление. Закон Ома в операторной форме
Рассмотрим вначале пассивные RLC-элементы и определим их операторные сопротивления.
Пусть через индуктивность при нулевых начальных условиях i
(0)=0
протекает ток i
(
t
)
, изображение которого I
(
P
)
.
По закону электромагнитной индукции напряжение на индуктивности:
Умножим обе части этого равенства на множитель 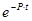 и выполним прямое преобразование Лапласа: и выполним прямое преобразование Лапласа:


По теореме дифференцирования оригинала, при i
(0)=0
, получим:

Отсюда получаем выражение для операторного сопротивления индуктивности:

(4.3)
Рассмотрим теперь емкость C
, которая при нулевых начальных условиях подключается к источнику напряжения UC
(
t
)
, изображение которого UC
(
P
)
.
Ток и напряжение на емкости связаны уравнением:

Применим к левой и правой частям этого выражения прямое преобразование Лапласа, в результате получим:

Отсюда находим операторное сопротивление емкости:
 . .
Рассмотрим теперь последовательный колебательный контур Рис.3.1, который при нулевых начальных условиях подключается к источнику 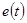 , изображение которогоE
(
P
)
. , изображение которогоE
(
P
)
.
По второму закону Кирхгофа можем записать (3.17):
 (4.5) (4.5)
Применим к этому уравнению прямое преобразование Лапласа, в результате, с учетом (4.3) и (4.4), получим:
  (4.6) (4.6)
или

где - операторное сопротивление последовательного колебательного контура.
Формула (4.6) представляет собой закон Ома в операторной форме. Нетрудно заметить, что структура операторного и комплексного сопротивлений подобны по форме:

Для перехода от комплексного сопротивления к операторному достаточно заменить j
*
w
на P
.
Сопротивление цепи в операторной форме есть новая более общая форма сопротивления, которая может применяться для решения задач, относящихся к любому режиму цепи при любой форме внешнего воздействия. Тогда как комплексное сопротивление применимо лишь при синусоидальном воздействии на цепь.
Наряду с операторным сопротивлением применяется операторная проводимость, которая, по определению, является величиной обратной сопротивлению.

4.4 Законы Кирхгофа в операторной форме
Первый закон Кирхгофа для мгновенных значений токов в узле электрической цепи:

Полагая, что каждый ток, входящий в узел или выходящий из него, имеет свое изображение Ik
(
P
)
, получим первый закон Кирхгофа в операторной форме:

который формулируется так: алгебраическая сумма изображений токов в узле электрической цепи равна нулю.
Соответственно второй закон Кирхгофа для любого замкнутого контура

где ek
(
t
),
Uk
(
t
)
- мгновенные значения э.д.с. и напряжений на пассивных элементах данного замкнутого контура, записывается в операторной форме:

Естественно, что при составлении уравнений по законам Кирхгофа в операторной форме необходимо задаться положительными направлениями всех токов и э.д.с., а также соблюдать все правила при составлении уравнений по законам Кирхгофа для действительных функций времени.
4.5 Эквивалентные операторные схемы
Вышеприведенные формулы (4.7) и (4.8), выражающие законы Кирхгофа в операторной форме справедливы при нулевых начальных условиях:
iL
(0)=0 и
UC
(0)=0.
Если до возникновения переходного процесса цепь обладала запасом энергии в виде электрического и магнитного полей, то, естественно, этот запас энергии необходимо учесть при составлении операторных уравнений. Надо ожидать, что законы Ома и Кирхгофа в этом случае изменяются в своей записи и примут более общую форму, из которой, как частный случай, должны вытекать формулы для нулевых начальных условий.
При ненулевых начальных условиях формула (4.3) принимает следующий вид:

гдеi
(0)
- ток через индуктивность в момент коммутации (t=0
).
Этому операторному уравнению соответствует следующая эквивалентная операторная схема замещения (Рис.4.1)
 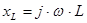 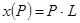
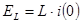
а) в)
Рис. 4.1. Исходная а) и в) операторная схема замещения индуктивности: EL
=
L
*
i
(0)
– внутренний источник напряжения, направление которого совпадает с направлением тока.
При ненулевых начальных условиях уравнение (4.4) принимает вид:

где UC
(0)
- напряжение на емкости в момент коммутации.
Операторному уравнению (4.10) соответствует следующая эквивалентная операторная схема замещения (Рис.4.2):
 

Рис. 4.2. Исходная а) и в) эквивалентная операторная схема замещения емкости
 - внутренний источник напряжения, направление которого противоположно направлению тока. - внутренний источник напряжения, направление которого противоположно направлению тока.
Расчет переходных процессов операторным методом сводится к выполнению следующих операций:
· вместо источников напряжений, оставшихся в цепи после коммутации, вводятся их операторные изображения e
(
t
)
®
E
(
P
)
;
· вместо всех искомых токов и напряжений на пассивных элементах вводятся пока неизвестные их изображения:

· вместо индуктивности и емкости рисуются их операторные схемы замещения, как показано на Рис.4.1 и Рис.4.2; при этом комплексные сопротивления заменяются операторными, а при ненулевых начальных условиях в операторную схему замещения вводятся внутренние источники напряжений


Активное сопротивление 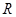 остается без изменений. остается без изменений.
Искомые изображения токов и напряжений могут быть определены любым известным методом расчета установившихся режимов (по законам Кирхгофа, методом контурных токов и др.).
Рассмотрим, для примера, электрическую схему Рис.4.3а, в которой до коммутации был установившийся режим. В момент коммутации t
=0
происходит короткое замыкание резистора R
1
и в цепи возникает переходной процесс.
Определим изображения токов в ветвях с индуктивностью и емкостью.
а) в)
Рис. 4.3. Исходная а) и ее операторная схема замещения в)
Операторный метод, как и классический, предусматривает, в первую очередь, определить независимые начальные условия.
В исходной схеме до коммутации был установившийся режим, при котором:

 Для определения неизвестных изображений токов через индуктивность и емкость составим операторную схему замещения (рис.4.3 в), а затем составим два уравнения по второму закону Кирхгофа: Для определения неизвестных изображений токов через индуктивность и емкость составим операторную схему замещения (рис.4.3 в), а затем составим два уравнения по второму закону Кирхгофа:


где

Отсюда определяем неизвестные изображения токов
 (4.11) (4.11)
4.6 Определение оригинала по известному изображению
Из вышеизложенного следует, что по законам Ома и Кирхгофа в операторной форме всегда можно найти изображения искомых токов и напряжений. После этого возникает обратная задача: по известному изображению тока или напряжения, например (4.11), найти соответствующий ему оригинал i
(
t
)
, т.е. найти закон изменения тока или напряжения в функции времени.
Для нахождения оригинала пользуются готовыми таблицами, которые приводятся в учебниках и справочниках, где приводятся изображения и соответствующие им оригиналы.
Однако, в настоящее время расчет переходных процессов операторным методом можно выполнять с помощью программы Mathcad, которая позволяет производить прямое и обратное преобразование не прибегая в таблицам: laplace, invlaplace.
На нескольких примерах покажем, как производится расчет переходных процессов операторным методом в среде Mathcad.
4.6.1 Расчет переходных процессов в цепях первого порядка операторным методом
Пример 4.1.
Рассчитать реакцию цепи RC (Рис.4.4) при воздействии на нее одиночного прямоугольного импульса.
Рис. 4.4. Одиночный прямоугольный импульс с напряжением E
и длительностью T
воздействует на цепь RC в момент t
=0
Для описания единичной функции в среде Mathcad имеется встроенная функция Хевисайда, Ф(
t
)
которая представляет собой источник постоянного напряжения в 1 В
.
Одиночный прямоугольный импульс, изображенный на Рис.4.4, описывается так:
U1
(t)=E*(
Ф
(t)-
Ф
(t-T)).
где Ф(
t
-
T
)
- функция Хевисайда, смещенная по оси времени вправо на T
.
Результаты расчетов переходных процессов в цепи RC, выполненные операторным методом в среде Mathcad, представлены на Рис.4.5.
Сравнение законов изменения напряжений на резисторе и емкости, полученные классическим методом Рис.2.2 и операторным методом Рис.4.5, показывает, что они совпадают.

Пример 4.2.
Рассчитать реакцию цепи RC (Рис.4.4) при подключении ее к источнику синусоидального напряжения.
Результаты расчетов представлены на Рис.4.6.
Сравнение Рис.4.6 с рис.2.6 показывает, что они совпадают.

Пример 4.3.
Рассчитать реакцию цепи RC (Рис.4.4), если входное напряжение представляет затухающую экспоненту.

Результаты расчетов представлены на Рис.4.7.

4.6.2 Расчет переходных процессов в цепях второго порядка операторным методом
Пример 4.4.
Рассчитать переходные процессы в последовательном колебательном контуре (Рис.4.8) операторным методом при подключении его к источнику постоянного напряжения U
1
(
t
)
.

Рис. 4.8. Последовательный колебательный контур при нулевых начальных условиях подключается к источнику напряжения U
1
(
t
)
.
Реакция цепи (Рис.4.8) при подключении ее к источнику постоянного напряжения U
1
(
t
)=E
представлена на Рис.4.9 и Рис.4.10 для критического и колебательного режимов соответственно.
Сравнение этих рисунков с результатами расчетов, выполненными классическим методом (Рис.3.3 и рис.3.4), показывает, что они совпадают.


Пример 4.5.
Реакция цепи RLC (Рис.4.8) при воздействии одиночного прямоугольного импульса (опер ХЕВИСАЙД LRC) показана на Рис.4.11.
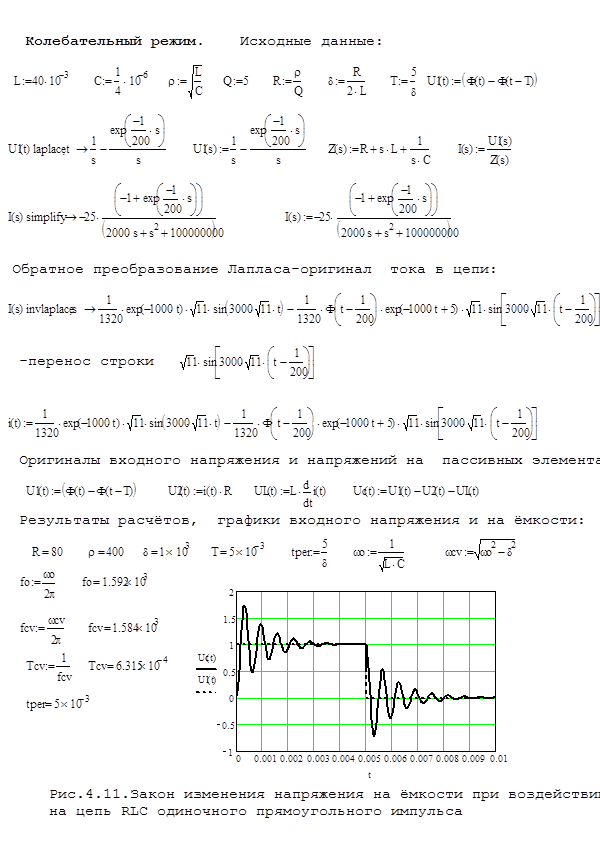


ЛИТЕРАТУРА
1. Атабеков Г.И. Основы теории цепей. Учебник для вузов. М., «Энергия», 1969 г. 424с. с ил.
2. Г.В. Зевеке Г.В., П.А. Ионкин, А.В. Нетушил, С.В. Страхов. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия» 1975 г. 752с. с ил.
3. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи: Учебник для электротехн., энерг., приборостроит. спец. вузов.-8-е изд., перераб. и доп.-М.: Высш. шк., 1984.-559с., ил.
4. Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники: В 2-х т. Учебник для вузов. Том 1.-3-е изд., перераб. и доп.-Л.: Энергоиздат. Ленингр. отд-ние, 1981.-536с., ил.
5. Дьяконов В. Д. Mathcad 2000: Учебный курс-СПб: Питер, 2000.-592с.: ил.
6. М. Херхагер, Х. Партоль Mathcad 2000 полное руководство: перевод с нем.-К.: Издательская группа BHV. 2000.-416с.
7.Карлащук В.И. Электронная лаборатория на IBMPC. Программа ElectronicsWorkbench и ее применение. «Салон-Р», 2000.-506с.
СОДЕРЖАНИЕ
Предисловие к 3-ей части
Глава 1. Основные сведения о переходных процессах в линейных электрических цепях
1.1 Возникновение и общая характеристика переходных процессов
1.2 Начальные условия
1.3 Математические основы анализа переходных процессов
Глава 2. Переходные процессы в цепях первого порядка
2.1 Общий алгоритм расчета переходных процессов в цепях первого порядка классическим методом
2.2 Переходные процессы в цепях RC при подключении ее к источнику постоянного напряжения и коротком замыкании
2.3 Переходные процессы в цепях RC при подключении ее к источнику синусоидального напряжения
2.4 Переходные процессы в цепях RL при подключении ее к источнику постоянного напряжения и коротком замыкании
2.5 Подключение цепи RL к источнику синусоидального напряжения
2.6 Синтез цепи RC с заданными параметрами переходного процесса
Глава 3 Переходные процессы в цепях второго порядка
3.1 Общая характеристика переходных процессов в цепях второго порядка
3.2 Алгоритм расчета переходных процессов в цепях второго порядка
3.3 Переходные процессы в последовательном колебательном контуре при подключении его к источнику постоянного напряжения
3.3.1 Апериодический режим
3.3.2 Критический режим
3.3.3 Колебательный режим
Глава 4. Операторный метод расчета переходных процессов в линейных электрических цепях
4.1 Общие сведения
4.2 Изображения простейших функций
4.3 Операторное сопротивление. Закон Ома в операторной форме
4.4 Законы Кирхгофа в операторной форме
4.5 Эквивалентные операторные схемы
4.6 Определение оригинала по известному изображению
4.6.1 Расчет переходных процессов в цепях первого порядка операторным методом
4.6.2 Расчет переходных процессов в цепях второго порядка операторным методом
Литература
|