В В Е Д Е Н И Е
Физика - наука о природе, изучающая наиболее общие свойства материального мира, наиболее общие формы движения материи, лежащие в основе всех явлений природы. Физика устанавливает законы, которым подчиняются эти явления.
Физика изучает также свойства и строение материальных тел, указывает пути практического использования физических законов в технике.
В соответствии с многообразием форм материи и ее движения физика подразделяется на ряд разделов: механика, термодинамика, электродинамика, физика колебаний и волн, оптика, физика атома, ядра и элементарных частиц.
На стыке физики и других естественных наук возникли новые науки: астрофизика, биофизика, геофизика, физическая химия и др.
Физика является теоретической основой техники. Развитие физики послужило фундаментом для создания таких новых отраслей техники, как космическая техника, ядерная техника, квантовая электроника и др. В свою очередь, развитие технических наук способствует созданию совершенно новых методов физических исследований, обуславливающих прогресс физики и смежных наук.
ФИЗИЧЕСКИЕ ОСНОВЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
| Лекция 1
|
Понятие состояния в классической механике. Кинематика материальной точки. Механическое движение, система отсчета. Скорость, ускорение. Радиус кривизны траектории, нормальное и тангенциальное ускорения. |
| Кинематика поступательного и вращательного движения твёрдого тела. Угловая скорость и ускорение, их связь с линейными. |
I.
Механика. Общие понятия
Механика - раздел физики, который рассматривает простейшую форму движения материи - механическое движение.
Под механическим движением понимают изменение положения изучаемого тела в пространстве со временем относительно некоторого гола или системы тел, условно считаемых неподвижными. Такую систему тел вместе с часами, в качестве которых может быть выбран любой периодический процесс, называют системой отсчета
(С.О.). С.О. часто выбирают из соображений удобства.
Для математического описания движения с С.О. связывают систему координат, часто прямоугольную.
Простейшее тело в механике - материальная точка. Это тело, размерами которого в условиях денной задачи можно пренебречь.
Всякое тело, размерами которого пренебречь нельзя, рассматривают как систему материальных точек.
Механика подразделяется на кинематику
, которая занимается геометрическим описанием движения, не изучая его причин, динамику,
которая изучает законы движения тел под действием сил, и статику, которая изучает условия равновесия тел.
2. Кинематика точки
Кинематика изучает пространственно-временное перемещение тел. Она оперирует такими понятиями, как перемещение 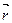 , путь , путь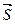 , время t , скорость движения , время t , скорость движения 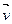 , ускорение , ускорение 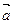 . .
Линию, которую описывает при своем движении материальная точка, называют траекторией. По форме траектории движения делятся на прямолинейные и криволинейные. Вектор 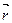 ,
соединяющий начальную I и конечную 2 точки, называют перемещением (рис. I.I). ,
соединяющий начальную I и конечную 2 точки, называют перемещением (рис. I.I).
Каждому моменту времени t соответствует свой радиус-вектор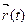 : :
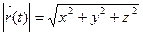
 Таким образом движение точки может быть описано векторной функцией. Таким образом движение точки может быть описано векторной функцией.
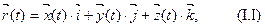
которая определяем векторный
способ задания движения, или тремя скалярными функциями
x=
x(
t);
y=
y(
t);
z=
z(
t) ,
(1.2)
которые называют кинематическими уравнениями. Они определяют задание движения координатным
способом.
Движение точки будет также определено, если для каждого момента времени будет установлено положение точки на траектории, т.е. зависимость
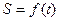 (1.3) (1.3)
Она определяет задание движения естественным
способом.
Каждая из указанных формул представляет собой закон
движения точки.
3. Скорость
Если моменту времени t1
соответствует радиус-вектор 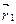 , а , а 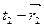 , то за промежуток , то за промежуток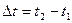 тело получит перемещение
тело получит перемещение 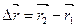 . В этом случае средней скоростью . В этом случае средней скоростью
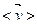 за Dt называют величину за Dt называют величину
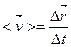 , (1.4) , (1.4)
которая по отношению к траектории представляет секущую, проходящую через точки I и 2. Скоростью
в момент времени t называют вектор
 , (1.5) , (1.5)
Из этого определения следует, что скорость в каждой точке траектории направлена по касательной к ней. Из (1.5) следует, что проекции и модуль вектора скорости определятся выражениями:
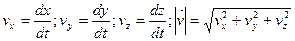 , (1.6) , (1.6)
Если задан закон движения (1.3), то модуль вектора скорости определится так:
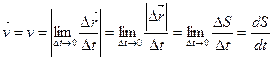 , (1.7) , (1.7)
Таким образом, зная закон движения (I.I), (1.2), (1.3), можно вычислить вектор и модуль доктора скорости и, наоборот, зная скорость из формул (1.6), (1.7), можно вычислять координаты и путь.
4. Ускорение
При произвольном движении вектор скорости непрерывно меняется. Величина, характеризующая быстроту изменения вектора скорости, называется ускорением 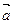 . .
Если в. момент времениt1
скорость точки 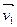 ,а приt2
- ,а приt2
- 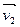 , то приращение скорости составит , то приращение скорости составит 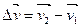 (Рис.1.2). Среднее ускорение (Рис.1.2). Среднее ускорение  при этом при этом
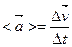 , (1.8) , (1.8)
а мгновенное
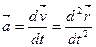 , (1.9) , (1.9)
Для проекции и модуля ускорений имеем: 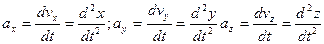 , (1.10) , (1.10)
Если задан естественный способ движения, то ускорение можно определить и так. Скорость меняется по величине и по направлению, приращение скорости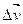 раскладывают на две величины; раскладывают на две величины;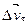 - направленный вдоль - направленный вдоль 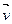 (приращение скорости по величине) и (приращение скорости по величине) и 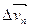 - направленный перпендикулярно - направленный перпендикулярно 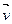 (приращение. скорости по направлению), т.е. (приращение. скорости по направлению), т.е. 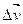 = =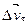 + +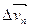 (Рис.I.З). Из (1.9) получаем: (Рис.I.З). Из (1.9) получаем:
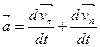 (1.11); (1.11);  (1.12) (1.12)
Тангенциальное (касательное) ускорение характеризует быстроту изменения 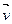 по величине по величине  (1.13) (1.13)
нормальное (центростремительное ускорение) характеризует быстроту изменения по направлению. Для вычисления a
n
рассмотрим
DOMN и DMPQ при условии малого перемещения точки по траектории. Из подобия этих треугольников находим PQ:MP=MN:OM :
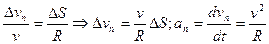 , (1.14) , (1.14)
Полное ускорение в этом случае определится так:
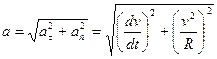 , (1.15) , (1.15)
5. Примеры
I. Равнопеременное прямолинейное движение. Это движение с постоянным ускорением(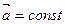 ) . Из (1.8) находим ) . Из (1.8) находим
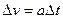 или или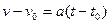 , где v
0
- скорость в момент времениt
0
. Полагая t
0
=0, находим
, где v
0
- скорость в момент времениt
0
. Полагая t
0
=0, находим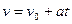 ,
а пройденный путь S
из формулы (I.7): ,
а пройденный путь S
из формулы (I.7):
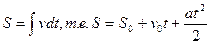 гдеS
0
- постоянная, определяемая из начальных условий. гдеS
0
- постоянная, определяемая из начальных условий.
2. Равномерное движение по окружности. В этом случае скорость меняется только по направлению, то есть 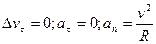 - центростремительное ускорение. - центростремительное ускорение.
| Лекция 2
|
Динамика материальной точки и поступательного движения твёрдого тела. Закон инерции. |
| Внешние и внутренние силы. Центр масс. Закон сохранения импульса. |
I. Основные понятия
Перемещение тел в пространстве - результат их механического взаимодействия между собой, в результате которого происходит изменение движения тел или их деформация. В качестве мары механического взаимодействия в динамике вводится величина – сила 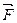 . Для данного тела сила - внешний фактор, а характер движения зависит и от свойства самого тела - податливости оказываемому на него внешнему воздействию или степени инерции тела. Мерой инерции тела является его масса т
, зависящая от количества вещества тела. . Для данного тела сила - внешний фактор, а характер движения зависит и от свойства самого тела - податливости оказываемому на него внешнему воздействию или степени инерции тела. Мерой инерции тела является его масса т
, зависящая от количества вещества тела.
Таким образом, основными понятиями механики являются: движущаяся материя, пространство и время как формы существования движущейся материи, масса как мера инерции тел, сила как мера механического взаимодействия между телами.Соотношения между этими понятиями определяются законам! движения, которые были сформулированы Ньютоном как обобщение и уточнение опытных фактов.
2. Законы механики
1-й закон.
Всякое тело сохраняет состояние покоя или равномерного прямолинейного движения, пока внешние воздействиянеизменяют этого состояния. Первый закон заключает в себе закон инерции, а также определение силы какпричины, нарушающей инерциальное состояние тела. Чтобы выразить его математически, Ньютон ввел понятие количества движения или импульса тела:
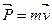 ( 2.1) ( 2.1)
тогда 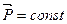 , если , если 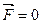
2-й закон.
Изменение количества движения пропорционально приложенной силе и происходит по направлению действия этой силы. Выбрав единицы измерения m
и 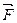 так, чтобы коэффициент пропорциональности был равен единице, получаем так, чтобы коэффициент пропорциональности был равен единице, получаем
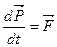 или или 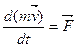 (2.2) (2.2)
Если при движении m
=
const
, то
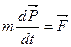 или или 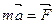 (2.3) (2.3)
В этом случае 2-й закон формулируют так: сила равна произведению массы тела на его ускорение. Этот закон является основным законом динамики и позволяет по заданным силам я начальным условиям находить закон движения тел. 3-й закон.
Силы, с которыми два тела действуют друг на друга, равны и направлены в противоположные стороны, т.е.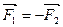 , (2.4) , (2.4)
Законы Ньютона приобретают конкретный смысл после того, как указаны конкретные силы, действующие на тело. Например, часто в механике движение тел вызывается действием таких сил: сила тяготения 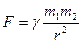 , где r - расстояние между телами, , где r - расстояние между телами,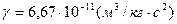 - гравитационная постоянная; сила тяжести - сила тяготения вблизи поверхности Земли, P
=
mg
; сила трения - гравитационная постоянная; сила тяжести - сила тяготения вблизи поверхности Земли, P
=
mg
; сила трения 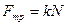 ,где k
- коэффициент трения, N -
сила нормального давления ; cила упругости ,где k
- коэффициент трения, N -
сила нормального давления ; cила упругости 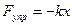 , где k
- коэффициент упругости (жесткости); x -перемещение тела. , где k
- коэффициент упругости (жесткости); x -перемещение тела.
3. Инерциальные системы отсчёта (И.С.О.)
Для описания движения тела необходимо указать систему отсчета. Существует целый ряд систем, в которых выполняются законы Ньютона и для которых верно утверждение, что когда тело приобретает ускорение, можно указать тела, действие которых вызывает это ускорение. Систему отсчета, в которой это утверждение, вытекающее из закона инерции, выполняется, называют инерциальной
. Любая С.O., движущаяся с постоянной скоростью (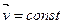 ) относительно инерциальной системы, сама будет инерциальной. Существует бесконечное множество И.С.О., движущихся друг относительно друга равномерно и прямолинейно. В таких системах: отсчета физические явления выглядят наиболее просто. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, будет неинерциальной.
В такой системе отсчета на тело действует сила инерции ) относительно инерциальной системы, сама будет инерциальной. Существует бесконечное множество И.С.О., движущихся друг относительно друга равномерно и прямолинейно. В таких системах: отсчета физические явления выглядят наиболее просто. Всякая система отсчета, движущаяся с ускорением относительно инерциальной, будет неинерциальной.
В такой системе отсчета на тело действует сила инерции 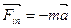 , где , где 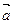 - ускорение системы отсчета, которая не является результатом взаимодействия тел. - ускорение системы отсчета, которая не является результатом взаимодействия тел.
4. Принципы относительности Галилея
Опыт показывает, что во всех инерциальных системах отсчета механические явления протекают одинаково, т.е. в механическом отношении все И.С.О. равноправны. Это утверждение называют принципом относительности Галилея.
5. Закон сохранения импульса
Совокупность взаимодействующих тел называют механической системой. Силы, действующие между телами системы, называют внутренними, а со стороны тел, не включенных в данную систему - внешними. Если действием внешних тел на тела данной системы можно пренебречь, то систему называют замкнутой или изолированной. В ней действуют лишь внутренние силы. В такой системе описать движение тел можно без помощи 2-го закона Ньютона, т.к. в ней имеются величины, на меняющиеся со временем, т.е. сохраняющиеся. Одной их таких величин является полны импульс всех тел системы. Рассмотрим взаимодействие двух материальных точек m1
и m2
составляющих замкнутую систему. Движение каждой из них описывается 2-й законом Ньютона:
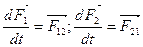 (2.5) (2.5)
Т.к. по третьему закону Ньютона 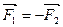 , то из (2.5) получаем: , то из (2.5) получаем:
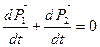 ,откуда ,откуда 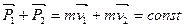 (2.6) (2.6)
Этот результат и представляет закон сохранения импульса для замкнутой системы.
Полный импульс всех тел замкнутой системы сохраняется (т.е. не меняется со временем).
Нужно помнить, что импульсы отдельных тел при этом могут меняться.
6. Реактивное движение
Закон сохранения импульса лежит в основе реактивного движения. Рассмотрим, например, движение ракеты,
где 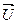 — скорость истечения газов — скорость истечения газов  относительно ракеты. Полный импульс системы ракета-газы для моментов времени t1
и t2
будет равен: относительно ракеты. Полный импульс системы ракета-газы для моментов времени t1
и t2
будет равен:
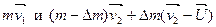 , ,
гдеDm
-
масса вылетевших газов, 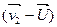 - их скорость относительно Земли, тогда - их скорость относительно Земли, тогда 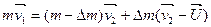 или или 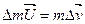 (2.7). Из этой формулы следует, ччо
отделение газов от ракеты эквивалентно действию на не силы: (2.7). Из этой формулы следует, ччо
отделение газов от ракеты эквивалентно действию на не силы: 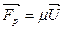 , где , где 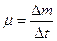 - расход топлива. Эту силу называют реактивной. Переходя в (2.7) к дифференциалам, получим - расход топлива. Эту силу называют реактивной. Переходя в (2.7) к дифференциалам, получим
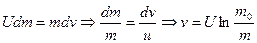 (2.8) (2.8)
Полученный результат представляет Формулу Циолковского.
7. Центр инерции
Рассмотрим движение произвольной системы материальных точек (Рис. 2.2). Движение каждой из них определяется законом изменения радиус-вектора изменения радиус-вектора 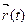 .Центром инерции
(центром масс) такой системы зазывается точка (т.С.), радиус-вектор которой равен: .Центром инерции
(центром масс) такой системы зазывается точка (т.С.), радиус-вектор которой равен:
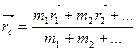 (2.9) (2.9)
Центр инерции может и не совпадать ни с одним из тел системы, а, например, для двух тел центр инерции делит расстояние между ними на части, обратно пропорциональные их массам. Вычислим скорость центра инерции:
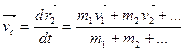 (2.10) (2.10)
Числитель этой формулы есть полный импульс 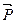 поэтому: поэтому:
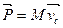 (2.11) (2.11)
Как видно, между полный импульсом системы тел и скоростью центра инерции такая же связь, как и для материальной т.С. массой 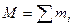 . Таким образом, центр инерции приобретает смысл точки, скорость которой равна скорости движения всей системы как целого. Если . Таким образом, центр инерции приобретает смысл точки, скорость которой равна скорости движения всей системы как целого. Если 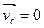 , то система как целое покоится, в то же время отдельные тела системы могут двигаться относительно центра инерции. , то система как целое покоится, в то же время отдельные тела системы могут двигаться относительно центра инерции.
Формула (2.11) есть обобщение закона инерции для системы тел: для замкнутой системы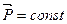 , .поэтому центр инерции такой системы движется равномерно и прямолинейно или покоится.
, .поэтому центр инерции такой системы движется равномерно и прямолинейно или покоится.
| Лекция
3
|
Энергия и работа силы. Кинетическая энергия. Силовое поле. Потенциальная энергия, её связь с силой. |
| Закон сохранения энергии (упругий и неупругий удар). |
I. Работа
Количественной характеристикой процесса взаимодействия тел является работа, совершаемая силой А.
Работа есть скалярная величина, равная произведению проекции силы (на направление перемещения) на величину перемещения точки приложения силы
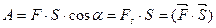 (3.1) (3.1)
гдеa
-
угол между направлением силы и перемещением. Если a
<90°. то сила совершает положительную работу (А>0), если a
>90°, то А<0; приa
=90° сила работы не совершает, oна лишь искривляет траекторию тела.
Если работа совершается переменной силойF=
F(
S)
, во для элементарного перемещения 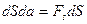 , а для всего пути , а для всего пути
 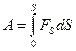 (3.2) (3.2)
Вычислим для примера работу, совершаемую силой тяжести при движении тела по наклонной плоскости (Рис. 3.1):
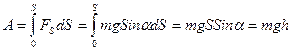 , ,
где h - высота наклонной плоскости. Как видно, работа силы тяжести не зависит от длины пути, а зависит от начального и конечного положений тела. Можно показать, что такой же результат получается для любой криволинейной траектории. Таким же свойством обладает и сила упругости.
Силы, обладающие указанным свойством, называются консервативными или потенциальными.
Для таких сил работа по любому замкнутому контуру равна нулю, или:
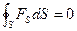 (3.3) (3.3)
Это и есть условие потенциального характера силы.
Работа, совершаемая за единицу временя, называется мощностью:
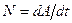
2. Энергия
В результате совершения работы в окружающих телах происходят определенные изменения - переход одних форм движения материи в другие. Общей количественной мерой различных форм движения материи является физическая величина, которую называют энергией Е
.
В физике соответственно различным физическим процессам и взаимодействиям различают механическую энергию; тепловую, электромагнитную, ядерную и т.д.
Энергия может, быть выражена через величины, характеризующие строение и состояние тела. Она является функцией его состояния. Изменение состояния тела, например, его движение, приводит к изменению его энергии, а сам процесс изменения есть результат работы, совершаемой силой, поэтому изменение энергии тела или системы тел определяется работой, совершенной приложенными к телу силами:
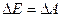 (3.4) (3.4)
Механическая энергия состоит из двух величин - кинетической энергии K - энергии движения и потенциальной энергии П - энергии взаимодействия между телами:
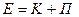 (3.5) (3.5)
3. Кинетическая и потенциальная энергии
Чтобы получить выражение для кинетической энергии подсчитаем работу силы, необходимую для изменения скорости тел от v
1
до v
2
:
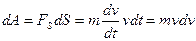
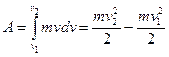
Итак, совершенная силой работа равна приращению кинетической энергии тела: 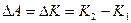 , где , где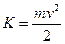 . Потенциальная энергия обусловлена характером взаимодействия между телами, их взаимным расположением. Поэтому вид формулы для потенциальной энергии зависит от конкретного вида силы. . Потенциальная энергия обусловлена характером взаимодействия между телами, их взаимным расположением. Поэтому вид формулы для потенциальной энергии зависит от конкретного вида силы.
Так, работа силы тяжести, необходимая дня изменения положения тела относительно Земли, равна:
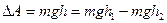 , ,
где h
1
и h
2
- начальная и конечная высота тела относительно Земли. Эта работа равна изменению потенциальной энергии тела:
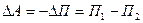 , ,
т.е. совершенная силой работа равна убыли потенциальной энергии тела.
Так как 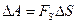 , то , то 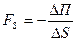 или или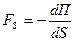 (3.7) (3.7)
Эта формула, связывающая между собой силу, перемещений тела и соответствующее этому изменение его потенциальной энергии, даёт возможность вычислить потенциальную энергию в отдельном случае.
Вычислим, например, потенциальную энергию силы тяготения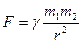
Из (3.7) находим 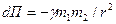 и и 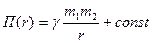 , , 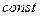 есть так называемый нулевой уровень потенциальной энергии, который обычно выбирается из условия есть так называемый нулевой уровень потенциальной энергии, который обычно выбирается из условия 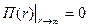 , тогда , тогда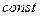 = 0 и = 0 и 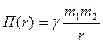
4. Закон сохранения механической энергии
В изолированной системе кроме полного импульса сохраняющейся величиной является и полная механическая энергия.
Так, для двух взаимодействующих материальных точек уравнения движения будут 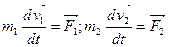 (3.8) (3.8)
Под действием сил точки совершают перемещения 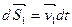 ; ; 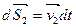 . Умножив каждое из уравнений (3.8) на соответствующее перемещение, получим: . Умножив каждое из уравнений (3.8) на соответствующее перемещение, получим:
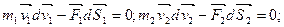 сложив их, получим: сложив их, получим:
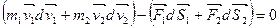 (3.9) (3.9)
т.к. 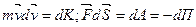 , то вместо (3.9) имеем: , то вместо (3.9) имеем:
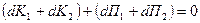 или или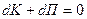 , ,
где 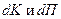 - изменение кинетической и потенциальной энергии всех тел системы. Тогда - изменение кинетической и потенциальной энергии всех тел системы. Тогда 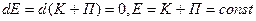 , (3.10) , (3.10)
Полная энергия изолированной системы есть величина постоянная. Это и есть формулировка закона сохранения энергии.
5. Удар абсолютно упругих и неупругих тел
Под ударом понимают кратковременное столкновение соударяющихся тел.
Прямая, проходящая через точку соприкосновения обоих тел, называется линией удара (Рис. 3.2). Если она проходит через центры масс тел, то удар центральный. Отношение относительных скоростей шаров после удара U
к скорости их v
до удара называют коэффициентом восстановления: 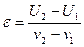  . Если . Если 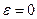 , то удар абсолютно неупругий, если , то удар абсолютно неупругий, если 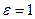 , то удар абсолютно упругий. , то удар абсолютно упругий.
При абсолютно неупругом ударе часть механической энергии тел переходит в другие формы энергии (например, в тепловую). В этом случае выполняется лишь закон сохранения импульса, на основании которого и находим скорость шаров после столкновения:
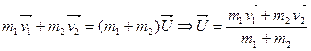 (3.11) (3.11)
Найдем изменение кинетической энергии шаров, т.е. ту её часть которая перешла во внутреннюю энергию:
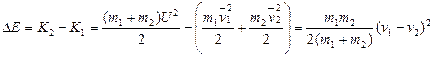 (3.12) (3.12)
При абсолютно, упругом ударе потерь энергии нет, н в этом случае выполняются законы сохранения импульса и энергии:
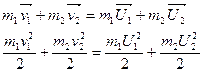
Решая эти уравнения, находим:
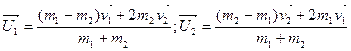 (3.13) (3.13)
Когда массы соударяющихся тел равны: 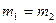 , то шары обмениваются скоростями: , то шары обмениваются скоростями: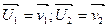
| Лекция
4
|
Динамика вращательного движения. Моменты силы и импульса относительно центра и оси. Уравнение динамики вращения. |
| Кинетическая энергия вращения, момент инерции. Закон сохранения момента импульса. |
I. Кинематика вращательного движения
Абсолютно твердым телом в механике называют совокупность частиц, взаимное расположение которых остается неизменным во время движения.
 Вращательным называют такое движение, при котором все точки тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения. Вращательным называют такое движение, при котором все точки тела описывают концентрические окружности, центры которых лежат на одной прямой, называемой осью вращения.
Положение вращающегося тела может быть определено взятым с соответствующим знаком двугранным углом j между двумя полуплоскостями, проходящими через ось вращения, одна из которых Q
неподвижна относительно С.О., а другая Р
связана с телом и вращается вместе о ним (рис. 4.1). Знак j определяют по правилу правого винта. Положение тела в любой момент времени t
определяется уравнением 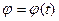 , дающим закон вращательного движения. , дающим закон вращательного движения.
Различные точки тела проходят при одинаковом угловом перемещении d
j
разные линейные перемещения d
S
, которые связаны соотношением:
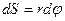 (4.1) (4.1)
где r
- расстояние от точки тела до оси вращения.
Поэтому вращательное движение удобно характеризовать не линейными, а угловыми величинами, одинаковыми для всех точек тела.
Угловой скоростью 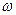 называют скорость изменения угла попорота: называют скорость изменения угла попорота:
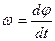 (4.2) (4.2)
Угловым ускорением 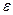 называют величину, характеризующую быстроту изменения угловой скорости: называют величину, характеризующую быстроту изменения угловой скорости:
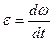 (4.3) (4.3)
С помощью (4.1) можно найти связь 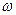 и и 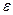 в с соответствующими линейными величинами в с соответствующими линейными величинами 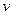 и и 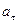 : :
 (4.4) (4.4) 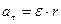 (4.5) (4.5)
Угловые скорость и ускорение - векторные величины, направленные вдоль оси вращения. Их направление определяют с помощью правила правого винта. Так, что:
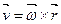 (4.6) (4.6) 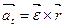 (4.7) (4.7)
Полное ускорение 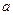 находится по формуле: находится по формуле:
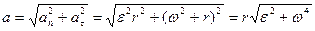 (4.8) (4.8)
2. Кинетическая энергия вращательного движения. Момент инерции.
Если дело вращается вокруг неподвижной оси, то его кинетическая энергия равна:
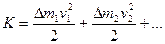 (Рис. 4.2.) (Рис. 4.2.)
 Используя формулу (4.4), получим Используя формулу (4.4), получим 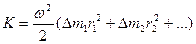
где 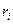 и и 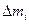 - расстояние i-частицы тела до оси вращения; - расстояние i-частицы тела до оси вращения; 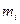 - её масса. - её масса.
Величина, стоящая в скобках, не зависит от скорости движения тела и характеризует инерционные свойства тела во вращательном движении: чем больше эта величина, тем большую энергию надо затратить для достижения данной скорости. Эта величина, характеризующая твердое тело, а также выбранную, ось вращения, называется моментоминерции тала относительно данной оси 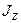 . Тогда кинетическую энергию можно записать в виде: . Тогда кинетическую энергию можно записать в виде:
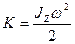 (4.9) (4.9)
Момент инерции тела вычисляют по формуле:
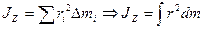 (4.10) (4.10)
 Для материальной точки, вращающейся вокруг оси, Для материальной точки, вращающейся вокруг оси, 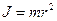 ; для шара, вращающегося вокруг оси, проходящей через его центр, ; для шара, вращающегося вокруг оси, проходящей через его центр, 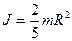 .Полная кинетическая энергия катящегося тела вычисляется по формуле: .Полная кинетическая энергия катящегося тела вычисляется по формуле:
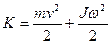 (4.11) (4.11)
Если известен момент инерции относительно оси, проходя через центр инерции тела 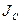 , можно вычислить момент инерция относительно параллельной оси (теорема Штейнера): , можно вычислить момент инерция относительно параллельной оси (теорема Штейнера):
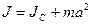 , (4.12) , (4.12)
где 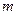 - масса тела, - масса тела, 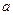 - расстояние между осями (Рис. 4.3). - расстояние между осями (Рис. 4.3).

3. Основное уравнение динамики вращательного движения
Рассмотрим цилиндр вращающийся вокруг неподвижной оси (Рис. 4.4) под действием постоянной касательной силы 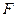 .За время .За время 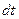 точка приложения силы переместится на точка приложения силы переместится на 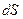 и работа этой силы будет и работа этой силы будет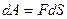 , которая равна приращению кинетической энергии: , которая равна приращению кинетической энергии: 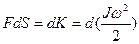 , т.к. , т.к. 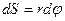 , то , то
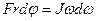 (4.13) (4.13)
Величину 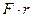 , равную произведению проекции силы на плоскость, перпендикулярную оси вращения, на рассотояние до оси вращения (плечо силы , равную произведению проекции силы на плоскость, перпендикулярную оси вращения, на рассотояние до оси вращения (плечо силы 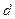 ), называют моментом силы относительно оси ), называют моментом силы относительно оси 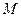 : :
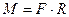 , (4.14) , (4.14)
Тогда вместо (4.13) запишем:
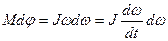 или или 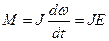 (4.15) (4.15)
Эта формула выражает основное уравнение динамики вращательного движения: момент силы относительно оси вращения равен произведению момента инерции относительно этой оси на угловое ускорение. Роль силы при вращательном движении играет, момент силы, массы - момент инерции. Момент силы - векторная величина, направленная вдоль оси вращения. Его направление определяется правилом правого винта.
4. Момент импульса. Закон сохранения момента импульса
При вращательном движении точки количественной мерой её движения является момент импульса точки относительно оси, который определяется по формуле:
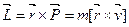 , (4.16) , (4.16)
где 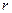 -
радиус окружности, по которой движется точка; -
радиус окружности, по которой движется точка; 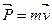 - её имульс - её имульс
Момент импульса вращающегося тала равен сумме моментов отдельных его частиц:
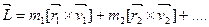
Если ось вращения неподвижна, то момент импульса вращающегося тела можно найти так:
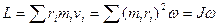 , (4.17) , (4.17)
где 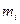 и и 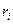 - масса и радиус вращения - масса и радиус вращения 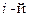 точки, точки, 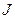 - момент - момент
инерции всего тела относительно выбранной оси вращения.
Используя эту формулу, основное уравнение вращательного движения можно записать в виде:
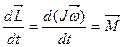 , (4.18) , (4.18)
Если на вращающееся тело не действуют внешние силы или их результирующий момент равен нулю, то момент импульса тела относительно оси вращения есть величина постоянная. Из (4.18) при 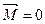 : :
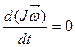 и и  (4.19) (4.19)
В изолированной системе полный момент импульса есть величина постоянная. Это есть закон сохранения момента импульса.
| Лекция 7 |
Основы релятивистской механики. Постулаты специальной теории относительности. Преобразование Лоренца. |
| Относительность длин и промежутка времени. Преобразование скоростей и ускорений в релятивистской кинематике. Понятие о релятивистской динамике. Закон взаимосвязи массы и энергии. |
I. Принцип относительности
 Как только тело начинает двигаться со скоростью, сравнимой со скоростью света в пустоте Как только тело начинает двигаться со скоростью, сравнимой со скоростью света в пустоте 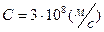 , рассмотренные законы механики (классическая механика) становятся неприменимыми.
В этом случае они заменяются более общими законами теории относительности (релятивистской теории). Основное содержание этой теории составляет доказательство принципа относительности - независимости физических процессов от выбора системы отсчета. Доказательство этого закона в инерциальных системах отсчета рассматривается в специальной теории относительности (С.Т.О.). Таким образом, теория относительности по называет, что законы природы не зависят от выбора системы отсчета, положения и движения наблюдателя, а результаты измерений в различных системах отсчета могут быть сопоставлены. , рассмотренные законы механики (классическая механика) становятся неприменимыми.
В этом случае они заменяются более общими законами теории относительности (релятивистской теории). Основное содержание этой теории составляет доказательство принципа относительности - независимости физических процессов от выбора системы отсчета. Доказательство этого закона в инерциальных системах отсчета рассматривается в специальной теории относительности (С.Т.О.). Таким образом, теория относительности по называет, что законы природы не зависят от выбора системы отсчета, положения и движения наблюдателя, а результаты измерений в различных системах отсчета могут быть сопоставлены.
В классической механике математическим выражением принципа относительности являлись преобразования Галилея
. позволявшие сопоставлять результаты измерении в разных И.С.О.
Для случая движения двух И.С.О., изображенных на рис. 5.1,
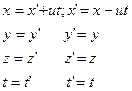 (5.1) (5.1)
где 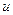 - скорость движения системы - скорость движения системы 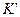 относительно относительно 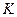 . Из формул (5.1) вытекает и классический закон сложения скоростей: . Из формул (5.1) вытекает и классический закон сложения скоростей:
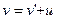
Эта формула оказалась неприменимой при определении скорости света по отношению к Земле (опыт Майкельсона и Морли, 1887 г.). Результат опыта показал, что скорость свата во всех инерциальных системах отсчета постоянна, она не зависит ни от скорости источника, ни от скорости приемника.
2. Постулаты Эйнштейна
Выход из создавшегося положения был найден Эйнштейном, который, анализируя опытные факты, сформулировал два постулата:
1. Не только механические, но и все физические процессы протекают одинаково во всех И.С.О.
2. Скорость света в вакууме есть величина постоянная.
Этих двух постулатов оказалось достаточно, чтобы разрешить все возникшие противоречия. Однако второй постулат оказался в противоречии с преобразованиями Галилея, из чего следовало, что преобразования Галилея необходимо было пересмотреть. Такой пересмотр оказался связанным с коренной ломкой представлений о пространстве и времени. В частности, из постулатов следует, что понятие одновременности, считавшееся само собой разумеющимся, не является абсолютным: в разных системах отсчета время течет по-разному 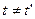 . .
3. Преобразования Лоренца
В С.Т.О. преобразования координат (5.1), описывающие переход от одной И.С.О. к другой, заменяются новыми соотношениями, которые удовлетворяют постоянству скорости света - преобразованиями Лоренца.
Для частного случая двух систем 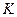 и и 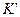 , находящихся в относительном движении вдоль оси , находящихся в относительном движении вдоль оси 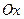 (Рис. 5.1), они имеют вид: (Рис. 5.1), они имеют вид:
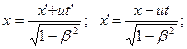
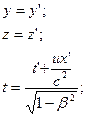 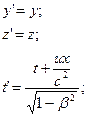 (5.3) (5.3)
где 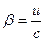 . .
Из этих формул видно, что при малых скоростях для 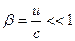 формулы (5.3) переходят в (5.1), следовательно, законы классической физики входят в С.Т.О. как частный случай. формулы (5.3) переходят в (5.1), следовательно, законы классической физики входят в С.Т.О. как частный случай.
Из преобразований Лоренца вытекают основные следствия.
4. Замедление времени
В направлении 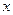 часы, связанные с системой часы, связанные с системой 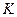 , измеряют интервал времени: , измеряют интервал времени: 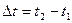 . При наблюдении в движущейся системе этот интервал становится равным . При наблюдении в движущейся системе этот интервал становится равным 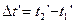
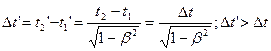 , (5.4) , (5.4)
Для движущегося наблюдателя время идёт медленнее.
5. Сокращение длин
Если в системе 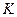 находится отрезок находится отрезок 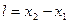 , то это же расстояние для движущегося наблюдателя в системе , то это же расстояние для движущегося наблюдателя в системе 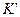 окажется равным: окажется равным:
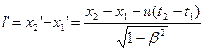
Так как наблюдатель видит в своей системе 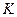 оба конца одновременно оба конца одновременно 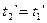 , то из формул обратного преобразования Лоренца , то из формул обратного преобразования Лоренца 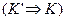 (5.3) получим (5.3) получим 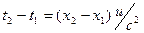 , откуда следует, что: , откуда следует, что:
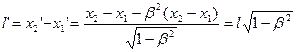 , (5.5) , (5.5)
Для движущегося наблюдателя длина отрезка кажется уменьшенной в направлении движения 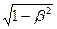 раз, т.е. движущемуся наблюдателю шар кажется сплющенным эллипсоидом. раз, т.е. движущемуся наблюдателю шар кажется сплющенным эллипсоидом.
6. Сложение скоростей в теории относительности.
Пусть некоторая точка М движется относительно системы 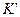 вдоль оси вдоль оси 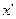 со скоростью со скоростью 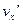 . Скорость её относительно неподвижной системы . Скорость её относительно неподвижной системы 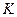 будет: будет:
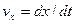 , (5.6) , (5.6)
Координата этой точки определится из формул (5.3):
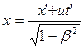 , откуда , откуда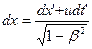 , (5.7) , (5.7)
Аналогично определяем 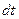 : :
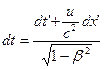 , (5.8) , (5.8)
Подставляя (5.7) и (5.8) в (5.6) и учитывая, что 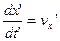 , получаем: , получаем:
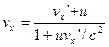 , (5.9) , (5.9)
Эта формула выражает релятивистский закон сложения скоростей. Сравнивая (5.9) с (5.2), видно, что при малых скоростях 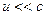 теорема сложения скоростей Галилея остаётся верной. Из формулы (5.9) следует предельный характер скорости света. Действительно, если относительно теорема сложения скоростей Галилея остаётся верной. Из формулы (5.9) следует предельный характер скорости света. Действительно, если относительно 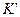 послать световой импульс со скоростью послать световой импульс со скоростью 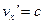 , то относительно , то относительно 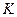 получим: получим:
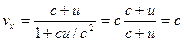 , ,
т.е. в системе 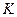 скорость светового импульса тоже равна скорость светового импульса тоже равна 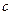 . Найдем другие составляющие скорости . Найдем другие составляющие скорости 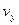 и и 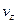 . .
Так как 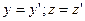 , то: , то:
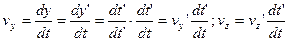 , (5.10) , (5.10)
Из формулы (5.3) находим:
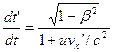
Подставляя это в (5.10), получим:
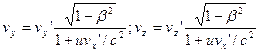 (5.11) (5.11)
7. Изменение массы со скоростью
В классической механике основной закон динамики имеет вид:
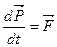 или при или при 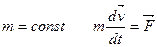
Из этой формулы следует, что при действии постоянной силы скорость может возрастать неограниченно:
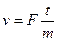 при при 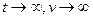
Этот результат противоречит теории относительности. Поэтому, естественно, сделать предположений, что масса как мера инертности должна зависеть от скорости: 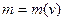 ,
так что при ,
так что при 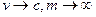 , т.к. при этой скорость тела будет ограничена. , т.к. при этой скорость тела будет ограничена.
Из преобразований Лоренца вытекает, что масса, определяемая как 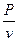 , является переменной, зависящей от скорости. Эта зависимость дается выражением: , является переменной, зависящей от скорости. Эта зависимость дается выражением:
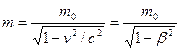 , (6.1) , (6.1)
где 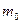 - масса покоя, т.е. в той С.О. где тело покоится, - масса покоя, т.е. в той С.О. где тело покоится, 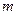 называют релятивистской массой. называют релятивистской массой.
Эта формула имеет очень большое значение и постоянно используется в атомной физика, где частицы двигаются со скоростями 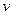 1111 1111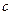 . Она была проверена экспериментально. . Она была проверена экспериментально.
Таким образом, в С.Т.О. основной закон динамики приобретает вид:
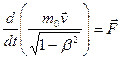 (6.2) или (6.2) или 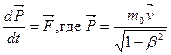 (6.3) (6.3)
8. Движение релятивистской частицы
Найдем закон движения релятивистской частицы, движущейся под действием постоянной силы 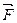 , которая в начальный момент , которая в начальный момент 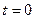 покоилась. покоилась.
Из формулы (6.2) находим:
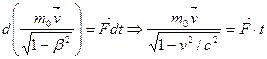 откуда откуда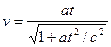 , (6.4) , (6.4)
где 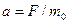 при малых при малых 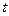 , , 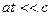 и и 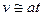 как и в классической механике; при как и в классической механике; при 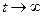 , , 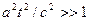 и и 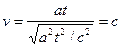
Путь, пройденный телом, будет равен 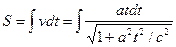 , вычисления дают: , вычисления дают: 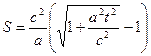 (6.5) (6.5)
при малых 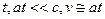 используя формулу используя формулу 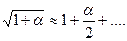 , получаем: , получаем:
 как в классической механике. как в классической механике.
9. Связь между массой и энергией
Энергия 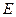 движущегося тела вызывается работой силы движущегося тела вызывается работой силы 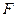 действующей на него, следовательно: действующей на него, следовательно:
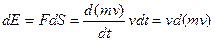 или или 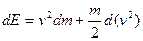 (6.6) (6.6)
Из формулы (6.1) получаем:
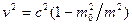 и и 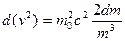
Подставляя эти выражения в (б.6), получаем:
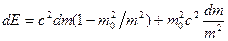 , откуда , откуда 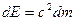
После интегрирования 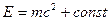 . Полагая . Полагая 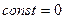 , получим энергию покоя тела , получим энергию покоя тела
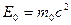 (6.7) и энергию движущегося тела (6.7) и энергию движущегося тела 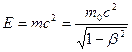 (6.8) (6.8)
Из формул (6.7) и (6.6) следует, что между массой и энергией существует неразрывная связь:
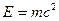 (6.9) (6.9)
Всякая масса 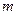 связана с определенным количеством энергии связана с определенным количеством энергии 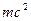 . .
В состоянии покоя с массой 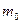 связана энергия покоя: связана энергия покоя:
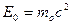
С другой стороны, с энергией 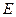 связана определенная масса: связана определенная масса:
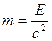
Изменение энергии влечет одновременно и изменение массы наоборот:
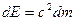
Фундаментальное соотношение (6.9) было впервые установлено Эйнштейном.
10. Кинетическая энергия. Энергия и импульс
Кинетическая энергия 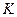 равна разности равна разности 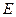 и и 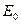 : :
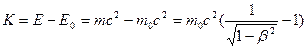 (6.10) (6.10)
При малых скоростях (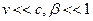 ) ) 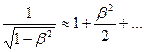 и из формулы (6.10) .получаем: и из формулы (6.10) .получаем:
 , ,
т.е. получим выражение для кинетической энергии в классической механике.
Исключив 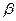 ив выражений ив выражений 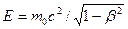 и и 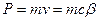 , находим соотношение между импульсом и энергией: , находим соотношение между импульсом и энергией:
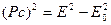 , откуда , откуда 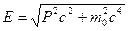 (6.10) (6.10)
Для частицы с массой покоя 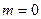 (фотон) имеем: (фотон) имеем:
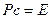
|