Билет №1
Что такое математическая модель экономического объекта?
Модель
– это материальный или мысленно представляемый объект, который в процессе исследования замещает объект-оригинал, так что его непосредственное: изучение дает новые знания об объекте-оригинале.
Математическая модель экономического объекта
- это его гомоморфное отображение в виде совокупности уравнений, неравенств, логических отношений, графиков. Гомоморфное отображение объединяет группы отношений элементов изучаемого объекта в аналогичные отношения элементов модели (создает условный образ объекта).
Экономико-математические модели можно подразделить на классы по ряду признаков.
1. По целевому назначению экономико-математические модели делятся на:
· теоретические, используемые при исследовании общих свойств и закономерностей экономических процессов;
· прикладные, используемые для решения конкретных экономических задач (модели экономического анализа, прогнозирование, управление).
2. по характеристике моделируемого объекта:
Экономико-математические модели могут предназначаться для исследования разных сторон народного хозяйства (производственно-технологической, территориальной) и его отдельных частей.
3. По исследуемым экономическим процессам и содержательной проблематике:
Выделяются модели народного хозяйства в целом и его отдельных подсистем – отраслей, регионов и т. д., комплексы моделей производства, потребления, формирования и распределения доходов, трудовых ресурсов, ценообразования, финансовых связей...
4. По способам отражения фактора времени:
· Статистические
· Динамические
В статических
моделях все зависимости относятся к одному моменту времени. Динамические
модели характеризуют изменение экономических процессов во времени.
Макроэкономические
модели описывают экономику страны как единое целое, связывая между собой укрупненные материальные и финансовые показатели: ВНП, потребление, инвестиции, занятость, ставку процента, денежные траты и др.
Микроэкономические
модели описывают взаимодействие структурных и функциональных составляющих экономики либо поведение отдельной такой составляющей в рыночной среде.
Различают дескриптивные и нормативные
модели. Дескриптивные
модели объясняют наблюдаемые факты или дают вероятностный прогноз. Нормативные
отвечают на вопрос: как это должно быть – т. е. предполагают целенаправленную деятельность.
В моделировании рыночной экономики особое место занимают равновесные модели. На их основе на микроэкономическом уровне моделируются оптимизационные модели. На макроуровне равновесные статические модели помогают исследовать состояние экономических систем.
Какие переменные в модели являются экзогенными, эндогенными?
При применении моделирования, Для решения поставленной задачи нужно построить математическую модель, наполнить ее информацией, а затем провести по ней необходимые расчеты. Вначале при построении модели нужно определить индексы, экзогенные и эндогенные переменные и параметры.
Для начала определяются экзогенные
переменные - те, которые задаются вне модели, т.е. известны заранее.
Далее вводятся обозначения для эндогенных
переменных - тех, которые определяются в ходе расчетов по модели и не задаются в ней извне.
Данные переменные делятся на 2 группы: показатели потоков и показатели запасов.
Поток
— показатель, характеризующий количество за определённый период времени.
Запас
— показатель, характеризующий количество на определённый момент, на какую-то дату.
Расскажите о классификации математических моделей экономики?
Математическая модель
– это описание объекта на математическом языке.
По способам выражения соотношений между внешними условиями, внутренними параметрами и искомыми характеристиками математические модели делятся на два основных типа: функциональные и структурные.
Основная идея функциональных моделей
– познание сущности объекта через важнейшие проявления этой сущности: деятельности, функционирования, поведения. Внутренняя структура при этом не изучается, а информация о структуре не используется. Функциональная модель имитирует поведение объекта так, что задавая значения «входа» X
,
можно получать значения «выхода» Y
. Построить функциональную модель – значит отыскать оператор D
,
связывающий X
и Y
:
Y
=
D
(
X
).
Структурные модели
отражают внутреннюю организацию объекта: его составные части, внутренние параметры и их связи с «входом» и «выходом».
Наиболее распространены два вида структурной модели:
· все неизвестные выражаются в виде функции от внешних условий и внутренних условий объекта:
 ; ;
· неизвестные определяются совместно, на основе системы отношений этого вида, т. е. уравнений, неравенств и т. д.:
 . .
По степени сложности математические модели экономических объектов и явлений подразделяются на несколько основных типов.
К первому типу относятся функциональные модели
, которые выражают прямые зависимости между известными (экзогенными) или неизвестными (эндогенными) величинами. Необходимые для построения модели параметры определяются на основе нормативных данных или статистическим способом.
Модели второго типа – это модели, выраженные с помощью систем уравнений относительно эндогенных величин. Они выражают обычно балансовое соотношение
между различными экономическими показателями и используются для нахождения сбалансированных плановых решений (например, модель межотраслевого баланса).
Третья группа - модели оптимизационного типа
. Основную часть такой модели составляют системы уравнений или неравенств относительно эндогенных величин. При этом необходимо найти такое решение этой системы, которое давало бы оптимальное (т. е. максимальное или минимальное в зависимости от постановки задачи) значение некоторого экономического показателя.
К четвертой группе относятся имитационные модели
, которые используются в составе человеко-машинных или игровых имитационных систем.
Пятую группу составляют более сложные образования – такие, как системы
и комплексы взаимосвязанных моделей
, относящихся к перечисленным выше типам.
Что такое производственная функция?
Производственными функциями
называют соотношения между используемыми в производстве материальными благами и трудовыми ресурсами (называемыми в совокупности производственными ресурсами), а также выпускаемой продукцией.
Пусть в модели рассматривается n
производственных ресурсов. Количество i
- го ресурса, используемого (или потребляемого) в течение некоторой единицы времени обозначим через xi
.
Пусть выпускается т
продуктов, причем объем выпуска j
-го продукта мы обозначим через yj
.
Производственная функция связывает значение вектора продукции y
со значениями вектора ресурсов х
:

Причем не учитываются эффекты, связанные с продолжительностью производственного цикла, т. е. с периодом между затратами ресурсов и выпуском продукции Вместо общего представления производственных функций в виде (1) часто используют два частных случая.
Описание элементарной производственной единицы начинается с формулировки списка ресурсов и номенклатуры продукции с указанием характерных значений и пределов изменения этих величин.
Материальные производственные ресурсы необходимо различать по способам их расходования в производственных процессах. Обычно выделяют материальные ресурсы двух типов: предмет труда (сырье) и основные фонды (здания, оборудование и т. д.). Ресурсы первого типа в процессе производства в течении одного производственного цикла (периода выпуска продукции) расходуются полностью. Ресурсы второго типа используются в течение значительного числа производственных циклов.
1. Функция выпуска,
в которой в качестве независимых переменных берутся затраты ресурсов, а функцией является выпуск:
 .
(2)
.
(2)
2. Функция производственных затрат,
в которой независимой переменной является выпуск, а функцией - затраты:
 .
.
В соотношениях (2) и (3) величины х, у
,
и а
могут быть многокомпонентными или векторными.
В функции затрат (3) задание выпуска продукции полностью определяет затраты ресурсов. Поэтому функция затрат используется в том случае, когда в описываемой элементарной экономической единице отсутствует возможность замещения одного ресурса другим.
Функция выпуска используется тогда, когда такая замена допустима. Как правило, в экономической литературе под производственной функцией подразумевают функцию выпуска.
С понятием производственной функции тесно связано понятие множество производственных возможностей,
которое определяется как множество всех возможных сочетаний затрат трудовых материальных ресурсов и выпусков продукции:
[
x
,
y
]
Î
G
(
a
),
(4)
где G
(
a
) -
некоторое множество G
в пространстве ресурсов и продуктов, зависящее от вектора параметра (а).
Множество производственных возможностей задается соотношением:
 ,
(5)
,
(5)
где а
-
параметр удовлетворяет соотношению  . .
Мультипликативная производственная функция и ее свойства?
Производственная функция (ПФ) выражает зависимость результата производства от затрат ресурсов.
Рассмотрим один из ее подвидов: мультипликационную функцию.
Мультипликативная ПФ задается выражением
X=AKa
1
La
2
a1>0 a2>0
где А - коэффициент нейтрального технического прогресса; а1, a2 -коэффициенты эластичности по труду и фондам . (K – соответственно фонды, L – труд)
Под техническим прогрессом в данной модели подразумевается вся совокупность качественных изменений труда и капитала. Таким образом, показатель технического прогресса является показателем времени. Технический прогресс называется нейтральным, так как он одинаково влияет на все задействованные для выпуска продукции ресурсы.
Свойства мультипликативной функции:
· При отсутствии одного из ресурсов производство невозможно.
Это означает, что каждый из ресурсов необходим хотя бы в малых количествах. Полное его отсутствие не может быть компенсировано другими ресурсами.
· При увеличении затрат производственных ресурсов выпуск продукции не уменьшается. Это означает, что предельные эффективности ресурсов положительны.
· С увеличением ресурсов скорость роста выпуска замедляется.
· При неограниченном увеличении одного из ресурсов, выпуск неограниченно растет.
Какова норма замены труда фондами и норма замены фондов трудом? Как связаны между собой эти величины?
В качестве ресурсов (факторов производства) на макроуровне наиболее часто рассматриваются накопленный труд в форме производственных фондов (капитал) К и настоящий (живой) труд L, а в качестве результата - валовой выпуск Х (либо валовой внутренний продукт Y, либо национальный доход N).
Норма замены труда фондами показывает, сколько нужно единиц фондов для компенсации выбывшей малой единицы труда, чтобы сохранить выпуск на прежнем уровне. И наоборот, норма замены фондов трудом показывает, сколько нужно единиц труда для замены выбывшей малой единицы фондов.
Что такое предельные эффективности фондов и труда?
Частные производные выпуска по факторам называются предельными продуктами или предельными (маржинальными) эффективностями факторов и представляют собой прирост выпуска на малую единицу прироста фактора:
- предельный продукт фондов, предельная фондоотдача (предельная эффективность фондов);
- предельный продукт труда, предельная производительность (предельная эффективность труда).
Что такое коэффициенты эластичности?
Коэффициент эластичности фактора показывает, на сколько процентов увеличится выпуск, если фактор возрастет на 1%.
Какой экономический смысл коэффициентов А, α1, α2, мультипликативной производственной функции?
Мультипликативная ПФ (МПФ) выпуска имее вид:
X=AKa
1
La
2
a1>0 a2>0
Величина X/L
называется средней производительностью труда, а величина X/K
средней производительностью ОПФ (средней фондоотдачей).
Частные производные выпуска по факторам называются предельными продуктами или предельными (маржинальными) эффективностями факторов, и характеризуют прирост выпуска на единицу прироста фактора:
 предельная фондоотдача (предельная эффективность фондов), предельная фондоотдача (предельная эффективность фондов),
 предельная производительность труда (предельная эффективность труда). предельная производительность труда (предельная эффективность труда).
Для МПФ предельная производительность труда пропорциональна с коэффициентом α2
средней производительности труда X/L
, а предельная фондоотдача – средней фондоотдаче X/K
с коэффициентом α1
:
 и и 
Т.е. а1 — эластичность выпуска по основным фондам, а a2 – эластичность выпуска по труду.
Дайте определение изокванты, изоклинали, расскажите о их свойствах?
Возможность взаимного замещения ресурсов означает, что одно и то же количество продукта у
может быть произведено различных сочетаниях ресурсов. Совокупность таких сочетаний ресурсов, т.е. точек в пространстве ресурсов, при котором может быть произведено определенное количество продукции у
,
называется изоквантой
иобозначается:
Q
(
y
0
) = {
x
:
f
(
x
) =
y
0
}.
Свойства изоквант:
· изокванты не пересекаются друге другом;
· изокванта Q
(
yo
)
разбивает неотрицательный ортант пространства ресурсов на 2 множества: в одном из которых у < уо
,
в другом у > уо
,
причем граница между этими множествами проходит по изокванте Q
(
yo
)
;
· большему выпуску продукции соответствует изокванта, более удаленна от начала координат;
· изокванты не имеют общих точек с осями координат.
Линии  называют изоклиналями
производственных функций с двумя ресурсами. Это функция одного ресурса от остальных при постоянной предельной норме замещения. Показывает при каких различных сочетаниях ресурсов может быть обеспечена одинаковая предельная норма замещения. называют изоклиналями
производственных функций с двумя ресурсами. Это функция одного ресурса от остальных при постоянной предельной норме замещения. Показывает при каких различных сочетаниях ресурсов может быть обеспечена одинаковая предельная норма замещения.
Свойства изоклиналей:
· Изоклинали ортогональны изоквантам.
· Для однородных функций они являются лучами, исходящими из начала координат.
Расскажите о характеристиках эффективности производства?
Эффективность производства
- это показатель деятельности производства по распределению и переработке ресурсов с целью производства товаров. Эффективность можно измерить через коэффициент - отношение результатов на выходе к ресурсам на входе или через объёмы выпуска продукции, её номенклатуры.
Суть проблемы повышения экономической эффективности производства состоит в том, чтобы на каждую единицу трудовых, материальных и финансовых ресурсов добиваться существенного увеличения объёма производства продукции. Это, в конечном счете, означает повышение производительности общественного труда, что и является критерием (мерилом) повышения эффективности производства.
Для характеристики эффективности производства используется ряд частных показателей, с помощью которых измеряется результативность применения отдельных видов ресурсов, среди которых следует выделить следующие:
1. Производительность
труда = результат / затраты живого труда (это прямой показатель)
Обратная величина есть трудоёмкость продукции:
Трудоёмкость = затраты времени / результат
2. Материалоотдача = результат / затраты материалов
Обратная этой величина есть материалоёмкость:
Материалоёмкость = затраты материалов / результат
3. Фондоотдача = результат / использованные фонды (капитал)
Обратная величина – Фондоёмкость = стоимость использованных основных фондов / результат.
Общим совокупным показателем эффективности производства выступает норма прибыли и уровень рентабельности. Прибыль в рыночных условиях выступает основной целью предпринимательства и критерием эффективности производства.
Производительность труда, качество продукции, ее материалоёмкость и фондоёмкость выступают основными слагаемыми эффективности производства. В условиях жесткой конкуренции в оценке эффективности производства возрастает значение конкурентоспособности, которая определяется рядом показателей, среди которых особое место занимают цена и качество продукции. В этой связи и на микроуровне, и на макроуровне важным показателем эффективности производства выступает улучшение качества продукции.
Что такое предельная норма замещения труда фондами?
Предельная норма замещения
одного ресурса другим показывает, сколько второго ресурса может быть высвобождено при увеличении затрат первого ресурса, если выпуск продукции остается неизменным.
Предельная норма замещения (γ)
имеет отрицательную величину, т. к. при уменьшении использования одного из ресурсов для сохранения выпуска продукции использование другого ресурса надо увеличить.
Вдоль изокванты верны следующие уравнения:
(Уравнения писала сама в маткаде, поэтому буквы красные: не обращай внимания)
Где уравнение изокванты:
Q(X
0
) = {(K, L
): F
(K, L
) = X
0}
Величину S
K
принято называть предельной нормой замещения труда фондами. Она показывает, сколько труда может быть высвобождено при увеличении затрат фондов, при постоянном выпуске.
Аналогично величину S
L
принято называть предельной нормой замещения фондов трудом. Она показывает, сколько фондов может быть высвобождено при увеличении затрат труда, при постоянном выпуске.
Как можно заметить, прослеживается обратно пропорциональная связь между объемом труда и объемом фондов.
Расскажите о модели межотраслевого баланса
Межотраслевой баланс (МОБ, метод «затраты-выпуск»)
— экономико-математическая балансовая модель, характеризующая межотраслевые производственные взаимосвязи в экономике страны. Характеризует связи между выпуском продукции в одной отрасли и затратами, расходованием продукции всех участвующих отраслей, необходимым для обеспечения этого выпуска. Межотраслевой баланс составляется в денежной и натуральной формах.
Межотраслевой баланс представлен в виде системы линейных уравнений. Межотраслевой баланс (МОБ) представляет собой таблицу, в которой отражен процесс формирования и использования совокупного общественного продукта в отраслевом разрезе. Таблица показывает структуру затрат на производство каждого продукта и структуру его распределения в экономике. По столбцам отражается стоимостный состав валового выпуска отраслей экономики по элементам промежуточного потребления и добавленной стоимости. По строкам отражаются направления использования ресурсов каждой отрасли.
Таблица межотраслевого баланса разделена на 4 квадранта:
1. Первый квадрант (верхний левый) отражает межотраслевые материальные связи. Они характеризуют текущее производственное потребление.
2. Во втором разделе баланса (в таблице справа от первого) отражена структура конечного продукта.
3. В третьем (он расположен под первым) — формирование стоимости конечного продукт как суммы чистой продукции и амортизации (т.е. отражена стоимостная структура ВВП).
4. В четвертом квадранте показываются элементы перераспределения и конечного использования национального дохода
Сформулируйте свойства продуктивности и прибыльности модели Леонтьева?
Предположим: в рассматриваемой экономической системе выпускается п
видов продуктов. В процессе производства своего вида продукта каждая отрасль нуждается в продукции других отраслей.
Введем обозначения: числа от 1 до n
– номера отраслей, величина a
ij
– объем продукции отрасли с номером i
, израсходованной отраслью j
в процессе производства единицы продукции. Число x
j
,
равно общему объему продукции (ВВ) j
-й отрасли за некоторый промежуток времени (например, плановый год), а значение y
j
,
показывает объем продукции j
-й отрасли, который был потреблен в непроизводственной сфере (объем КП), числа x
ij
– объем продукции i
-й отрасли расходуемый отраслью j
в процессе производства балансовые уравнения имеют вид:
Σx
ij
= x
i
– y
i
. i
= 1, 2,..., n
.
Матрица А =
(a
ij
) – матрица прямых затрат несет много информации о структуре межотраслевых связей. Сравнивая такие матрицы, составленные в достаточно разнесенные моменты времени, можно проследить направления изменения и развития технологии. Для осуществления объема x
j
ВВ продукции отрасли j
необходимо и достаточно произвести затраты в объемах x
j
a
ij
, i
== 1, 2, ..., n
продукции всех отраслей. Обозначим через X
вектор ВВ, X
= (x
1, x
2, …, x
n
). Тогда часть общего ВВ, израсходованная на производственные нужды в процессе производства определяется вектором
(Σa
1j
x
j
, Σa
2j
x
j
, . . ., Σa
nj
x
j
). (3.2)
В матричных обозначениях вектор производственных затрат равен AХ
. Тогда свободный остаток равный Y = X – AX
будет использован на непроизводственные цели и накопление. Основной вопрос, возникающий в планировании производства на заданный период, однако, формулируется, как правило, наоборот: при заданном векторе Y
КП требуется решить систему:
X – AX = Y
, X
≥ 0. (3.3)
Условие неотрицательности вектора X
создает определенные трудности при исследовании вопроса о существовании решения системы (3.3).
Приведенные выше уравнения вместе с изложенной интерпретацией матрицы A
и векторов X
, Y
называется моделью Леонтьева. В том случае когда решение системы (3.3) существует для любого неотрицательного вектора Y конечного спроса, говорят, что модель Леонтьева (и матрица А
) продуктивна.
Особенность матриц A
в модели Леонтьева состоит в том, что все элементы этой матрицы неотрицательны (A
≥ 0).
Рассмотрим балансовую модель, двойственную к модели Леонтьева (модель равновесных цен). Обозначим через p =
(p
1
, p
2
, …, p
n
) – вектор цен, i
-я координата которого равна цене единицы продукции i-
й отрасли; тогда i
-я отрасль получит доход, равный pixi.
Часть дохода эта отрасль потратит на закупку продукции у других отраслей. Так, для выпуска единицы продукции ей необходима продукция первой отрасли, второй отрасли и т.д. соответственно в объемах a
1i
, a
2i
, ..., a
ni
. На покупку этой продукции ею будет затрачена сумма
a
1
i
p
1
+
a
2
i
p
2
+ . .. +
a
ni
p
n
.
Для выпуска x
i
единицы продукции затраты составят
x
i
(a
1i
p
1
+ a
2i
p
2
+...+ a
ni
p
n
).
Оставшуюся часть дохода, называемую добавленной стоимостью, обозначим через V
i
(эта часть дохода идет на выплату зарплаты и налогов, предпринимательскую прибыль и инвестиции).
Таким образом, имеет место следующие уравнения:
p
i
– (a
1i
p
1
+ a
2i
p
2
+ ... + a
ni
p
n)
= v
i
, i =
1, 2, ..., n
, (3.5)
где v
i
– норма добавленной стоимости (добавленная стоимость на единицу выпускаемой продукции). Найденные равенства могут быть записаны в матричной форме следующим образом:
p
− A
T
p
= v ,
(3.6)
где v
– вектор норм добавленной стоимости, A
T
– матрица транспонированная для A
. Полученная система уравнений является двойственной к системе уравнений модели Леонтьева.
Система (3.6) называется прибыльной, если она разрешима в неотрицательных p
≥ 0.
Продуктивность и прибыльность модели Леонтьева эквивалентны: из продуктивности следует прибыльность и наоборот.
Какой смысл имеют коэффициенты технологической матрицы А модели Леонтьева?
Технологическая матрица А (матрица Леонтьева)
используется для моделирования экономик по методу «затраты – выпуск». Технологическая матрица А вводится как квадратная матрица коэффициентов затрат, названных «прямыми», на основе канонической формы системы линейных уравнений. Элементы матрицы А – aik
показывают, сколько продукции, выпущенной i-ой системой, надо затратить для производства единицы продукции k-ой системы.
Технологические коэффициенты для производимых товаров можно представить квадратной технологической матрицей:

Подставим в матрицу технические коэффициенты:

В матричных обозначениях эта система уравнений принимает вид:

Матричную форму модели прямых затрат принято записывать в виде │1 - A│x = 0 , где А – квадратная матрица коэффициентов затрат aik размером I*I ; 1– единичная диагональная матрица; x – вектор затрат размером I. Локальные потоки затрат xik
i-ой системы зависят от общих затрат xk
k-ой системе xik
=aik
xk
. Тогда общий объем прямых затрат i-ой системы равен сумме локальных затрат на приобретение продуктов у других систем
Метод межотраслевого анализа
Создатель теории межотраслевого анализа экономических систем - Василий Васильевич Леонтьев. По определению академика А. Г. Гранберга, сущность и сила межотраслевого анализа В. В. Леонтьева состоит в соединении теории функционирования экономических систем, метода математического моделирования, приемов систематизации и обработки экономической информации. Типичный продукт и вместе с тем предмет межотраслевого анализа –
межотраслевой баланс экономики. Это и система показателей, характеризующих соотношения, структуру, связи экономики, и математическая модель, позволяющая не только изучать взаимовлияние множества экономических величин, но и конструировать возможные (альтернативные) состояния экономики.
Экономическая система, для исследования которой применяется метод межотраслевого анализа, может быть большой, как народное хозяйство страны или даже вся мировая экономика, или малой, такой как экономика региона или даже одного предприятия.
В любом случае подход в основном один и тот же. Структура производственного процесса в каждом секторе представляется определенным вектором структурных коэффициентов, который количественно характеризует связь между затратами этого сектора и результатами его деятельности. Взаимозависимость между секторами рассматриваемой экономики описывается системой линейных уравнений, выражающих балансы между совокупными затратами и агрегированным выпуском каждого продукта и услуг, производимых и используемых в течение одного или нескольких промежутков времени.
Соответственно, технологическая структура системы в целом может быть представлена матрицей технологических коэффициентов «затраты-выпуск» всех ее секторов. В то же время эта матрица содержит множество параметров, на которых основываются балансовые соотношения.
Таблица межотраслевого баланса
Таблица межотраслевого баланса описывает потоки товаров и услуг между всеми секторами народного хозяйства в течение фиксированного периода времени, например года.
Упрощенный пример такой таблицы, отражающий трех-секторную экономику приведен в табл. 1.
Таблица 1
| Изß |
В=> |
Сектор 1
Сельское хозяйство |
Сектор 2
Промышленность |
Сектор 3
Домашнее хозяйство
|
Общий выпуск
|
| Сектор 1
. Сельское хозяйство |
20 |
30 |
50 |
100 т зерна |
| Сектор 2
Промышленность |
100 |
300 |
100 |
500 т стали |
| Сектор 3
Домашнее хозяйство |
60 |
110 |
30 |
200 человеке лет труда |
Девять чисел, составляющих основное содержание таблицы, характеризуют межсекторные потоки. Каждый сектор производит продукцию, часть которой используется внутри него самого, остальная часть распределяется и потребляется другими секторами.
В столбцах числа описывают структуру затрат соответствующего сектора. То есть, сколько нужно одной отрасли потребить собственного продукта и продукта других отраслей , чтобы произвести определенное количество своего совокупного продукта.
Предполагается, что все числа в табл. 1 представляют количества или, по крайней мере, физические индексы количеств определенных товаров или услуг. Более детализированная таблица межотраслевого баланса позволяет получить более определенную характеристику каждого отдельного числа.
Балансовые уравнения
Всю производимую отраслями продукцию удобно разделить на две части: промежуточный продукт и конечный продукт.
Промежуточный продукт
- это та часть совокупного продукта, которой производители обмениваются между собой или используют для собственных нужд.
Конечный продукт
- это продукция, предназначенная для потребителей.
Сектор конечного спроса
- это сектор, где потребляется конечный продукт -домашние хозяйства, экспорт, правительственные закупки.
Обозначения: U
–
общий выпуск; V–
промежуточный продукт; k
–
конечный продукт.
Объем продукции данной отрасли равняется сумме потоков продукции этой отрасли в другие отрасли, продукции, потребляемой в данной отрасли, и конечного продукта данной отрасли. Следовательно, баланс между совокупным выпуском и суммарными затратами продукции каждого сектора, показанный нашем примере, может быть описан следующей системой уравнений:
 . .
Эти уравнения называются балансовыми уравнениями производства. Для экономики с n
отраслями балансовые уравнения будут иметь вид:

Изложенная модель получила название модели «затраты-выпуск», или модели межотраслевого анализа (англ.: Input - OutputAnalysis).
Технологические коэффициенты
Объем выпуска сектора i
, используемого сектором j
при производстве единицы его совокупного выпускаj
, обозначается символом aij
и называется технологическим коэффициентом затрат продукта i
в секторе j
.
Представим вычисление технологических коэффициентов для примера трехсекторной экономики в табличном виде (табл. 3).
Таблица 3
| Отрасль
|
Межотраслевые потоки в
экономической системе
|
Общий выпуск
|
| 1
|
2
|
Конечный спрос
|
| 1
|
a11
=V11
/U1
=0.2 |
a12
=V12
/U2
=0.06 |
k13
|
U1
|
| 2
|
a21
=V21
/U1
=1.0 |
a22
=V22
/U2
=0.6 |
k23
|
U2
|
| Конечный спрос
|
a31
=V31
/U1
=0.6 |
a32
=V32
/U2
=0.22 |
k33
|
U3
|
Множество всех коэффициентов затрат всех секторов рассматриваемой экономики, представленной в форме прямоугольной таблицы, соответствующей таблице межотраслевого баланса, называется структурной матрицей этой экономики. Технологические коэффициенты образуют следующую квадратную матрицу n
-го порядка:

На практике структурные матрицы обычно вычисляются на основе межотраслевого баланса в стоимостном выражении. Но во всех случаях коэффициенты затрат должны интерпретироваться как отношения двух количеств, измеренных в физических единицах.
Решение системы балансовых уравнений
Из определения технологических коэффициентов вытекает:

Следовательно, балансовые уравнения можно записать так:

Или в матричной форме:

Введя обозначения:

получим матричное уравнение откуда: откуда: 
Умножим полученное уравнение на (Е-А)-1
:
 
откуда:

Планирование материального производства начинается с определения размеров и структуры общественного продукта. Решение матричного уравнения позволяет определить плановый объем производства отдельных продуктов таким образом, чтобы получить необходимые количества конечных продуктов. Полученное выражение позволяет быстро разработать разные варианты плана материального производства в соответствии с вариантами заданного конечного общественного продукта.
Введем обозначение:
 
Тогда можем записать:

Умножив, получим:
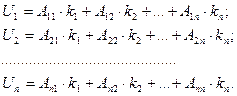
Данное уравнение показывает, что элементы матрицы 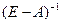 есть величины, определяющие количественные соотношения между конечными продуктами всех отраслей и продуктами каждой отрасли. Постоянные Aij
показывают, насколько увеличится выпуск Ui
сектора i
при увеличении kj
,
т. е. количества товара j
, потребляемого домашними хозяйствами (или любым другим потребителем этого сектора) на единицу. есть величины, определяющие количественные соотношения между конечными продуктами всех отраслей и продуктами каждой отрасли. Постоянные Aij
показывают, насколько увеличится выпуск Ui
сектора i
при увеличении kj
,
т. е. количества товара j
, потребляемого домашними хозяйствами (или любым другим потребителем этого сектора) на единицу.
В качестве примера рассмотрим нашу трехсекторную экономику, где матрица технологических коэффициентов равна:

Примем два варианта потребности в конечном продукте:
1. k1
= 50; k2
= 100,
2. k1
= 75; k2
= 110.
Тогда



Для второго варианта имеем:

С помощью модели межотраслевого баланса решаются и другие задачи: определение занятости в производстве; определение совокупных затрат труда; распределение совокупного общественного продукта и.т.д.
Билет №21
Определение цен продукта
Цены в системе межотраслевых связей определяются из системы уравнений, каждое из которых устанавливает, что цена единицы выпуска соответствующего производственного сектора должна быть равна совокупным издержкам в процессе производства этой продукции (в расчете на единицу выпуска). В эти издержки входит не только оплата затрачиваемых ресурсов, но и добавленная стоимость, которая представляет собой в основном платежи секторам конечного спроса (di
). Эти платежи состоят обычно из зарплаты, процента на капитал, предпринимательской прибыли, налогов, выплачиваемых правительству и другим секторам конечного спроса.
Обозначим через pi
цену единицы i
-го продукта. Тогда балансовые уравнения можно записать так:
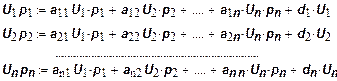
Сократив в обеих частях уравнений Ui
получим систему уравнений:

или в матричной форме:

где А
T
-
транспонированная матрица технологических коэффициентов, а р
и D -
вектора цен и платежей секторам конечного спроса соответственно.
Матричное уравнение можно представить в виде:
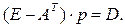
откуда получим в окончательном виде:
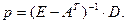
Данное уравнение позволяет определить соответствующую цену продукт отрасли. Элементы матрицы  измеряют зависимость цены р
j
продукции сектора j
добавленной стоимости di
,
полученной в секторе i
в расчете на единицу продукции этого сектора. измеряют зависимость цены р
j
продукции сектора j
добавленной стоимости di
,
полученной в секторе i
в расчете на единицу продукции этого сектора.
В применявшемся выше примере добавленная стоимость, выплаченная в сельском хозяйстве и промышленности (т. е. зарплата), в расчете на единицу выпуска составляет 0,6 и 0,22 соответственно. Транспонированная матрица технологических коэффициентов равна:
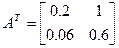
Далее рассчитываем:
 , , 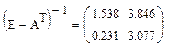
Тогда цены равны:
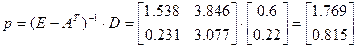 , ,
т. е. цены на сельскохозяйственную и промышленную продукцию, используемые при расчете стоимостных показателей межотраслевых потоков.
Внутреннее единство стоимостных и физических взаимосвязей в рамках открытой системы межотраслевых связей подтверждается следующим тождеством:

В левой части соотношения находится общая сумма добавленных стоимостей, выплаченная секторами системы секторам конечного спроса; в правой части - сумма стоимостей продуктов, доставленных всеми секторами секторам конечного спроса.
Билет №22
Разработка плана предприятия методом межотраслевого анализа
Метод межотраслевого анализа применим и для такой экономической системы, как предприятие. В этом случае место отраслей займут цеха, а конечного продукта - товарная продукция предприятия. Допустим, что предприятие состоит из п
производственных цехов, производящих однородные продукты 1, 2, ..., п.
Основа технико-экономического плана промышленного предприятия есть система технико-экономических норм. В эту систему входят:
1. Нормы затрат .продуктов собственного производства в отдельных цехах; эти нормы можно представить в виде матрицы:
2. Нормы расхода сырья, основных материалов, топлива и электроэнергии на единицу продукта, произведенного в соответствующем цехе; эти нормы можно записать в виде матрицы:
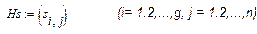 . .
3. Нормы времени работы машин и оборудования; эти нормы можно представить в виде матрицы:
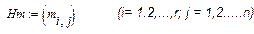 . .
4. Нормы, определяющие время работы отдельных групп персонала, необходимое для производства единицы продукта в соответствующем цехе; эти нормы можно представить в виде матрицы:
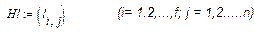 . .
Обозначим через Ui
совокупную продукцию i
-го цеха, а через ki
, - товарную продукцию этого цеха, т. е. ту часть совокупной продукции, которая остается после обеспечения производственных цехов и предназначается для сбыта. Поскольку затраты продукции i
-го цеха на единицы продукта j
-го цеха определяются по матрице ,(i,j = 1,2,...,n)
можно записать следующую систему уравнений: ,(i,j = 1,2,...,n)
можно записать следующую систему уравнений:

или в матричной форме:
U=
HzU +
K.
Решение, данного уравнения есть матрица:
U=(
E -
Hz)-1
К.
Отсюда следует, что матрица продукции есть произведение матрицы норм полных затрат продуктов, произведенных отдельными цехами, и вектора плановой товарной продукции предприятия.
Матрица Hs
норм расхода сырья, материалов, топлива и электроэнергии есть основа плана материально - технического снабжения. Из матрицы Hs
следует, что расходы отдельных видов сырья и материалов составляют:

или в матричной форме:
R =
HsU.
Подставляя выражение для определения матрицы товарной продукции, получаем:
R =
Hs(
E-
Hz)-
l
K.
Элементы произведения Hs(
E-
Hz)-
l
можно назвать коэффициентами полных затрат сырья и материалов. Матрицу потребности в сырье и материалах можно получить, умножив матрицу коэффициентов полных затрат сырья и материалов на вектор товарной продукции.
Матрица Н
m
-
основа плана использования машин и оборудования. Использование машин и оборудования в производстве составляет:
 , ,
или в матричной форме:
M = Н
m
U = Н
m (
E-
Hz)-1
К.
Элементы матрицы Н
m (
E-
Hz)-1
называются коэффициентами полного иcпользования машин и оборудования. Матрицу плана использования машин оборудования можно получить, умножив матрицу коэффициентов полного иcпользования машин и оборудования на вектор товарной продукции.
Матрица h
l-
основа плана по труду. Матрица рабочей силы есть:
L =
Hl.
U =
h
l(
E-
Hz)-1
К.
Элементы произведения h
l(
E-
Hz)-1
1
называются коэффициентами полных затрат рабочей силы. Матрица плановых затрат рабочей силы представляет собой произведение матрицы коэффициентов полных затрат рабочей силы и вектора товарной продукции.
Матричная форма технико-экономического плана в значительной мере упрощает планирование и уменьшает его трудоемкость: она позволяет быстро разработать различные варианты технико-экономического плана
Билет №23
Свойства производственных функций
Обратимся к некоторым наиболее общим свойствам производственных функций, имеющих форму 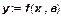 ,
т. е. функций выпуска, допускающих замещение одного ресурса другим. Рассмотрим в данном разделе функции с одним продуктом и несколькими ресурсами – трудовыми и материальными. ,
т. е. функций выпуска, допускающих замещение одного ресурса другим. Рассмотрим в данном разделе функции с одним продуктом и несколькими ресурсами – трудовыми и материальными.
Вектор параметров а
в данном соотношении будем опускать, считая, что параметры уже определены и их влияние нас не интересует. Тогда функция выпуска приобретает вид:
 ,
(8) ,
(8)
где:  - вектор. - вектор.
Соотношение (8) задано при неотрицательных значениях компонентов вектора х
.
Обычно относительно производственной функции (8) делают предположение, очень удобное с математической точки зрения, - о непрерывном изменении переменных х
и достаточно плавном изменении выпуска при изменении затрат ресурсов. В математической форме эти предположения имеют следующий вид: функция (8) задана при всех неотрицательных значениях составляющих вектора х
и является непрерывной или нужное число раз дифференцируемой функцией своих аргументов.
Перейдем к формулировке предположений (свойств), имеющих под собой экономическое обоснование. Для этого нам потребуются показатели предельного анализа.
Частная производная производственной функции по одному из ресурсов является предельной производительностью (эффективностью) данного ресурса -
¶
f/
¶
xi
. Она характеризует скорость изменения функции выпуска по отношению к изменению затрат ресурса. Если предельная производительность ресурса положительна, то, следовательно, выпуск растет при росте затрат ресурса. Если предельная производительность ресурса отрицательна, то выпуск уменьшается при росте затрат ресурса.
Средней производительностью ресурса будет показатель f(
x)/
xi
.
Относительной характеристикой изменения выпуска продукции при увеличении затрат ресурсов будет показатель эластичности выпуска по отношению к изменению затрат i
-го ресурса:

Эластичность выпуска по отношению к изменению затрат ресурса показывает, на сколько процентов возрастет объем продукции при увеличении затрат ресурсов на 1%.
Величину 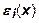 можно вычислить по другой, эквивалентной формуле: можно вычислить по другой, эквивалентной формуле:

Определим данные показатели для производственной функции у
= х
a
при х >
0
. Предельная эффективность ресурса равна:
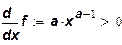
Средняя эффективность ресурса равна:
 . .
В силу того, что 0 < а <
1, для этой производственной функции предельна эффективность меньше средней.
Эластичность выпуска по ресурсу будет равна:
 = =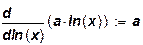
Эта производственная функция характеризуется постоянной эластичностью выпуска по отношению к изменению ресурса.

Рис. 3
На рис. 3 изображен график производственной функции  ,
ее предельной и средней эффективностей, а также эластичности выпуска по ресурсу. ,
ее предельной и средней эффективностей, а также эластичности выпуска по ресурсу.
Теперь сформулируем экономические предположения.
Первое предположение
. Производство невозможно при отсутствии хотя бы одного ресурса (точнее незаменимого ресурса), т. е.
 ; (5) ; (5)
Это означает, что каждый из ресурсов необходим хотя бы в малых количествах. Полное его отсутствие не может быть компенсировано другими ресурсами.
Второе предположение.
При увеличении затрат производственных ресурсов выпуск продукции не уменьшается. Это означает, что предельные эффективности ресурсов положительны. В математической форме:
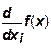 ≥0. (10) ≥0. (10)
Предположение (10), являющееся на первый взгляд очевидным, выполняется не всегда. Например, при возрастании количества удобрений, приходящихся на единицу площади, производство зерна сначала растет, а затем начинает снижаться. Поэтому для производственных функций, не удовлетворяющих соотношению (10), вводится понятие экономической области
. Использование ресурсов в сочетаниях, не попадающих в экономическую область, бессмысленно с экономической точки зрения.
Для функций (8), имеющих непрерывные производные, границами экономической области являются поверхности¶
f/
¶ х
i
= 0
, которые называют разделяющими поверхностями.
Третье предположение.
По мере увеличения количества одного ресурса при постоянных количествах других предельная эффективность использования этого ресурса не возрастает. Математически это требование для дважды дифференцируемых функций выглядит следующим образом:
 ≤0, ≤0, 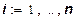 . (11) . (11)
Для производственной функции вида  это условие выполняется. Оно означает, что рост вооруженности средствами производства приводит к росту выпуска продукции, но темп роста выпуска продукции все время падает. В случае экстенсивного роста производства, т. е. роста только за счет количества ресурсов без повышения эффективности их использования на основе достижений научно-технического прогресса, соотношение (11) имеет разумную интерпретацию: поскольку каждая следующая единица производственного ресурса, количество которого возрастает, должна соединиться со все меньшим приходящимся на нее количеством других ресурсов, эффективность использования этого ресурса уменьшается. это условие выполняется. Оно означает, что рост вооруженности средствами производства приводит к росту выпуска продукции, но темп роста выпуска продукции все время падает. В случае экстенсивного роста производства, т. е. роста только за счет количества ресурсов без повышения эффективности их использования на основе достижений научно-технического прогресса, соотношение (11) имеет разумную интерпретацию: поскольку каждая следующая единица производственного ресурса, количество которого возрастает, должна соединиться со все меньшим приходящимся на нее количеством других ресурсов, эффективность использования этого ресурса уменьшается.
Часто вместо условия (11) формулируется более сильное математическое требование, близкое к (11) по смыслу. Если f(
x)
– выпуклая вверх функция своих аргументов, на неотрицательном ортанте для любых двух неотрицательных векторов х'
и х"
и любого числа а
Î
[0,1]
справедливо неравенство:
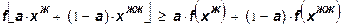 . (12) . (12)
Если используется единственный ресурс, а функция f(
x)
достаточно гладкая то требования (11) и (12) равносильны. Если же ресурсов несколько то (11) не эквивалентно (12), т. е. не эквивалентно выпуклости вверх функции f(
x)
.
Четвертое предположение
. Производственная функция характеризуется определенной отдачей от расширения масштабов производства. Последняя характеризует изменение выпуска продукции при пропорциональном изменении затрат ресурсов и математически выражается в умножении всех компонентов вектора х
на положительный скаляр t
.
Скалярная функция f(
x)
является однородной функцией степени δ
, если для любого вектора х
и любого скаляра t
она удовлетворяет соотношению:
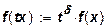 .
(13) .
(13)
Математически четвертое предположение состоит в требовании однородности производственной функции. Если δ > 1
, то производственная функция характеризуется возрастающей отдачей от расширения масштабов производства; если δ=1
– постоянной отдачей; при δ< 1
- убывающей отдачей. Естественно, что выполняется предположение δ ≥ 1
, ибо в противном случае нарушалось бы условие (10) во всех точках положительного ортанта и отсутствовала бы экономическая область. Данное предположение выполняется далеко не для всех производственных функций, используемых в экономических исследованиях. Для характеристики последствий изменения масштаба производства вводят показатель ε(х),
называемый эластичностью производства
и определяемый следующие образом:
 (14) (14)
Этот показатель характеризует процентное изменение выпуска продукции при изменении масштаба производства на 1% при данной структуре ресурсов х. Для производственных функций, удовлетворяющих соотношению (13), получаем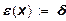 . .
Можно установить связь между эластичностью производства и эластичностью выпуска по отношению к изменению затрат ресурсов ε
i
(х)
. Учитывая, что
 , (15)
, (15)
тогда
 = = = = (16) (16)
Таким образом, эластичность производства в некоторой точке пространстве ресурсов равна сумме эластичности выпуска по отношению к затратам производственных ресурсов в этой точке.
В случае единственного ресурса, например в функции (6), эластичность производства совпадает с эластичностью выпуска по отношению к изменению затрат ресурса. Для производственных функций с постоянной отдачей от расширения масштабов производства (13) связь между эластичностями выпусков и эластичностью производства приобретает вид:
 . (17) . (17)
Рассмотрим производственные функции, удовлетворяющие четырем сформулированным выше предположениям, а именно: (9), (11). (13), (17). Возьмем t
,
удовлетворяющее условиям 0 < t
< 1. Из условия (12) получаем:
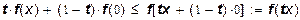 . .
Поскольку в силу (9) имеем 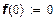 , то , то 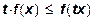 . Из соотношения (13) получаем . Из соотношения (13) получаем  , т. е. для выпуклых вверх производственных функций имеет место невозрастающая отдача от увеличения масштаба производства. Если производственная функция является строго выпуклой, условие (12) выполняется со знаком строгого неравенства (δ < 1). Это означает, что отдача от увеличения масштаба может быть только убывающей. Таким образом, для производственных функций, удовлетворяющих четырем соотношениям, в силу (17) и неотрицательности эластичности выпуска по ресурсам существует ограничение по эластичности выпуска: , т. е. для выпуклых вверх производственных функций имеет место невозрастающая отдача от увеличения масштаба производства. Если производственная функция является строго выпуклой, условие (12) выполняется со знаком строгого неравенства (δ < 1). Это означает, что отдача от увеличения масштаба может быть только убывающей. Таким образом, для производственных функций, удовлетворяющих четырем соотношениям, в силу (17) и неотрицательности эластичности выпуска по ресурсам существует ограничение по эластичности выпуска:
 . (18) . (18)
 Таким образом, в основе производствен. функций лежат предположения, приведенные на рис.4. Таким образом, в основе производствен. функций лежат предположения, приведенные на рис.4.
Билет №24
Возможности замещения ресурсов
Возьмем производственную функцию с двумя ресурсами:
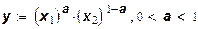 . (19)
. (19)
Функции такого типа часто используются при описании народного хозяйства или его структурных единиц. В таких производственных функциях величина у
имеет смысл конечной продукции народного хозяйства, x1
- общего количества основных фондов, x2
- общего количества трудовых ресурсов в стране.
Функция (19) удовлетворяет всем предположениям предыдущего раздела, причем для нее δ= 1. Поэтому можно построить функцию φ(х)
, которая в данном случае будет показывать объем продукции на 1 трудящегося и имеет вид:
 , ,
где χ
-
отношение количества основных фондов к численности трудящихся, т. е. фондовооруженность.
График функции  совпадает в этом случае с графиком производственной функции с одним ресурсом. Возможность взаимного замещения ресурсов означает, что одно и то же количество продукта у
может быть произведено различных сочетаниях ресурсов. Совокупность таких сочетаний ресурсов, т.е. точек в пространстве ресурсов, при котором может быть произведено определенное количество продукции у
,
называется изоквантой
иобозначается: совпадает в этом случае с графиком производственной функции с одним ресурсом. Возможность взаимного замещения ресурсов означает, что одно и то же количество продукта у
может быть произведено различных сочетаниях ресурсов. Совокупность таких сочетаний ресурсов, т.е. точек в пространстве ресурсов, при котором может быть произведено определенное количество продукции у
,
называется изоквантой
иобозначается:
Q(
y0
) = {
x:
f(
x) =
y0
}.
(20)
Рассмотрим произвольный луч в пространстве ресурсов, исходящий из начала координат и лежащий в положительном ортанте. Математически этот луч описывается как множество:
L = {
x:
x =
tx0
,
t≥0},
x0
≥0.
Согласно соотношению (13), получается, что для точек луча L
имеет место соотношение:
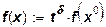
Если  и и 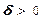 , то при достаточно больших t
выпуск продукции на луче может достичь любых предварительно заданных величин, в том числе и y0
. , то при достаточно больших t
выпуск продукции на луче может достичь любых предварительно заданных величин, в том числе и y0
.
Пусть 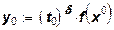 тогда в точке х* = тогда в точке х* =
 луч L
пересекается с изоквантой Q(
yo)
.
В точках луча, лежащих ближе к началу координат, т. е. t <
t0
,
выполняется соотношение у < уо
.
А в точках луча, лежащих от начала координат дальше чем точка х*, имеем у > уо
.
Поскольку данное утверждение верно для любого луча с положительным направляющим вектором х° -
таким, что
луч L
пересекается с изоквантой Q(
yo)
.
В точках луча, лежащих ближе к началу координат, т. е. t <
t0
,
выполняется соотношение у < уо
.
А в точках луча, лежащих от начала координат дальше чем точка х*, имеем у > уо
.
Поскольку данное утверждение верно для любого луча с положительным направляющим вектором х° -
таким, что  , то можно сделать следующие выводы о свойствах изоквант: , то можно сделать следующие выводы о свойствах изоквант:
- изокванты не пересекаются друге другом;
- изокванта Q(
yo)
разбивает неотрицательный ортант пространства ресурсов на 2 множества: в одном из которых у < уо
,
в другом у > уо
,
причем граница между этими множествами проходит по изокванте Q(
yo)
;
- большему выпуску продукции соответствует изокванта, более удаленна от начала координат;
- изокванты не имеют общих точек с осями координат.
Одна из изоквант производственной функции 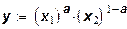 изображена на рис. 5. Луч L представлен на рисунке отрезком ОА.
Изокванта Q(
yo)
представляет собой зависимость X2(xi). Уравнение изокванты (20) задает эту зависимость неявно: изображена на рис. 5. Луч L представлен на рисунке отрезком ОА.
Изокванта Q(
yo)
представляет собой зависимость X2(xi). Уравнение изокванты (20) задает эту зависимость неявно: 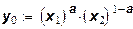
В явном виде получаем
 (21) (21)
Рис. 5.Функция х2
(х1
),
имеющая смысл количества трудовых ресурсов, необходимых для получения заданного конечного продукта в зависимости от использующегося объема основных фондов, является монотонно убывающей функцией. При ¶
f/
¶ х
2
> 0
вдоль изокванты выполняется соотношение:
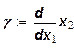 = =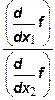 (22) (22)
Из условия (11) получается, что γ≤0
, а при строгой положительности предельных эффективностей ресурсов γ < 0
. Величину γ
принято называть предельной нормой замещения
одного ресурса другим. Она показывает, сколько второго ресурса может быть высвобождено при увеличении затрат первого ресурса, если выпуск продукции остается неизменным.
Предельная норма замещения γ
имеет отрицательную величину, т. к. при уменьшении использования одного из ресурсов для сохранения выпуска продукции использование другого ресурса надо увеличить. На рис. 5 предельная норма замещения а совпадает по величине с тангенсом угла φ
. Можно заметить, что 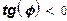 , а угол φ
и величина γ
меняются при движении вдоль изокванты , а угол φ
и величина γ
меняются при движении вдоль изокванты 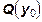
Для производственной функции 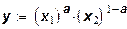 имеем: имеем:
 (23) (23)
Из формулы следует, что для функции (19) абсолютная величина предельной нормы замещения труда основными фондами обратно пропорций фондовооруженности х1
/х2
.
Этот факт можно легко объяснить: увеличение фондовооруженности приводит к уменьшению количества трудовых ресурсов, высвобождаемых каждой новой единицей основных фондов. Такой результат тесно связан со свойством (13) функции (19).
Линии 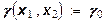 называют изоклиналями
производственных функций с двумя ресурсами. Для функции (19) изоклинали имеют вид: называют изоклиналями
производственных функций с двумя ресурсами. Для функции (19) изоклинали имеют вид:
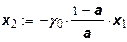
На рис. 6 представлены две изокванты, Q
(у0
) и Q (у1
),
и три изоклинали соответствующие значениям нормы замещения,  , ,  и и  , где , где  для производственной функции (19). для производственной функции (19).

Рис. 6
Величины углов φ1
,φ2
и φ3
удовлетворяют соотношению:
 , ,
а уравнения изоклиналей выглядят так:

В данном случае изоклинали имеют особенно простой вид – они являются лучами, исходящими из начала координат.
Такое свойство имеют изоклинали для важного класса производственных функций - однородных функций.
Для количественной характеристики скорости изменения предельной нормы замещения вдоль изокванты используется понятие эластичности замещения ресурсов
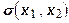 :
:
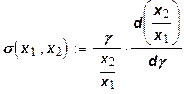 (24)
(24)
Эластичность замещения ресурсов имеет следующий экономический смысл – она приближенно показывает, на сколько процентов должно измениться отношение ресурсов при движении вдоль изокванты, чтобы при этом предельна норма замещения у
изменилась на 1%.
Для производственной функции (19) эластичность замещения ресурсов имеет простую геометрическую интерпретацию: поскольку изоклинали этой функции – прямые линии, то отношение х2
/х1
характеризуется тангенсом угла наклона изоклинали (см. рис. 5). Поэтому величина δ
показывает, на сколько процентов необходимо повернуть изоклиналь (т. е. изменить tgξ
), чтобы tgφ
изменился на 1%.
Как и в случае эластичности выпуска по ресурсу, эластичность замещения ресурсов также может быть представлена в более удобной форме:

Для производственной функции (19), учитывая соотношение
 , получаем: , получаем:
 =1 =1
Постоянство эластичности замещения ресурсов σ
многих производственных функций позволяет охарактеризовать с ее помощью возможность замещения ресурсов в целом (а не при каком-то конкретном соотношении ресурсов, как удается на основе предельной нормы замещения γ
). Чем больше σ, тем в более широких пределах производственные ресурсы могут замещать друг друга.
Все изложенные понятия, относящиеся к анализу замещения ресурсов в производственных функциях с двумя ресурсами, могут быть обобщены и на случай произвольного числа ресурсов. Понятие изокванты (20) с самого начала введено для произвольного числа ресурсов. Продифференцировав функцию вдоль изокванты, получим:
 .
(25) .
(25)
Зафиксируем затраты всех ресурсов, кроме i-
ro и j
-го. Получаем соотношение:
 , ,
которое полностью совпадает с соотношением (21) для производственной функции с двумя ресурсами. Это дает возможность ввести предельную норму замещения для ресурсов i
и j:
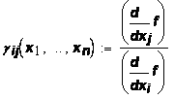 (25) (25)
где . Величина . Величина  характеризует отношения между малыми изменениями количеств этих ресурсов при сохранении выпуска на прежнем уровне. характеризует отношения между малыми изменениями количеств этих ресурсов при сохранении выпуска на прежнем уровне.
Можно ввести понятие эластичности замещения ресурсов i
и j:
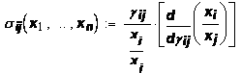 = = (26)
(26)
где по-прежнему меняются объемы только двух ресурсов, i
-го и j
-го, а производная берется вдоль изокванты.
Эластичность замещения ресурсов i
и j
приближенно показывает, на сколько процентов должно измениться отношение ресурсов i
и j
,
чтобы при этом предельная норма замещения этих ресурсов изменялась на 1%.
Итак, основными показателями анализа замещения ресурсов являются параметры, приведенные в табл. 1.

Билет №25
Линейная функция
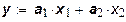
У данной функции предельные производительности факторов постоянны, эластичность замены факторов - бесконечна. Функция может использоваться в тех случаях, когда вклад каждого ресурса независим, например: производственная система состоит из отдельных производственных единиц, каждая из которых использует свой собственный производственный ресурс, подходящий только для этого производства.
Билет №26
Функция Аллена
 . .
Такая функция предназначена для описания производственных процессов, в которых чрезмерный рост любого из факторов оказывает отрицательное воздействие на объем выпуска. Обычно такая функция используется для описания мелкомасштабных систем с ограниченными возможностями переработки ресурсов.
Билет №27
Функция с линейной эластичностью замены факторов (функция
LES)
 . .
Функция LES применяется для описания производственных процессов, у которых (в отличие от описываемых функцией CES) возможность замещения вовлекаемых факторов существенно зависит от их пропорций, причем при низком уровне отношений х1
/х2
близка к единице, а с ростом отношения х1
/х2
-
неограниченно возрастает. Такая ситуация возможна, например, если рост ресурсов х1
связан с общим расширением производства, появлением множественных технологических процессов с широкими возможностями комбинирования.
Билет №28
Функция Солоу
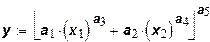 . .
Характеризуется тем, что величина процентного изменения предельной нормы замещения факторов, вызванного увеличением любого фактора на один процент, не зависит от начального уровня фактора. Эта функция может использоваться, когда влияние на объем выпуска увеличения каждого из факторов проявляется различным образом.
Билет №29
Ограниченная функция
CES
 . .
Функция предназначена для выражения двухрежимного производственного процесса, в котором один из режимов характеризуется отсутствием заменяемости факторов, другой - ненулевой постоянной величиной эластичности замены При этом переход от одного режима к другому осуществляется в зависимости от уровня, лимитирующего первый режим фактора.
Билет №30
Многорежимная функция
 . .
Одна из наиболее общих форм производственных функций. Она используется при описании процессов, в которых уровень отдачи каждой новой единицы ресурса скачкообразно меняется в зависимости от соотношения факторов. Функцию целесообразно применять при наличии информации о числе режимов n
и о
ширине «переходной» области между режимами (чем выше а
0
, тем более отчетливо выделяются режимы).
Билет №31
Функция линейного программирования
 . .
Функцию имеет смысл использовать в тех случаях, когда выпуск продукции является результатом одновременного функционирования k
-фиксированных технологий, использующих одни и те же ресурсы.
Билет №32
Описание технического прогресса
При построении производственных функций научно-технический прогресс может быть учтен с помощью множителя 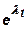 , где параметр λ
, характеризует темп прироста выпуска под влиянием научно-технического прогресса: , где параметр λ
, характеризует темп прироста выпуска под влиянием научно-технического прогресса:
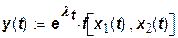 , ,  . .
Данная производственная функция является примером динамической производственной функции. Она включает нейтральный, то есть не материализованный в одном из факторов технический прогресс. Другим подходом является .выражение технического прогресса от прироста основных фондов в году t
или от инвестиций в научные исследования, что эконометрически предпочтительней В более сложных случаях технический прогресс может воздействовать непосредственно на производительность труда или капиталоотдачу:
 , ,
где К
-
основные фонды; L
-
трудовые ресурсы; A(
t)
и B(
t)
-
заданные функции времени, причем А(
t)
описывает повышение эффективности использования основных фондов;
B(
t)
-
трудовых ресурсов.

Билет №33
Функция затрат и их свойства
Рассмотрим функцию выпуска у
=
f(х)
с
одним продуктом и единственным ресурсом. Пусть эта функция - непрерывно дифференцируемая и удовлетворяет условиям:
f(0)=0
; f’(
x)>0
,при х>0
. (1)
В этом случае существует непрерывно дифференцируемая обратная функция: х =
h(
y)
.
Это – функция затрат. В качестве примера функции f(х)
можно рассмотреть функцию выпуска
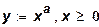
представленную в виде функции затрат
 . .
Рассмотрим свойства функции затрат x= с(у
).
Из условия f(0)=0
следует, что
с(0) = 0
, (2)
т. е. в случае отсутствия выпуска продукции тратить ресурс нет необходимости. Из условия f''(
x)>0
,при х>0
следует, что
c'(
y) =
l/
f'(
x)>0
,
(3)
это означает, что с ростом выпуска продукции затраты ресурса растут. Функцию c'(у)
принято называть предельными затратами ресурсов. Как видно из (3), предельные затраты ресурса обратно пропорциональны предельной эффективности ресурсов.
Предположим, что для функции f(х)
выполнено предположение об убывании предельной эффективности ресурса, т. еf''(х) <0
. Тогда из (3) получаем, что функция с'(у)
монотонно возрастает и
с"(у)>0
.
(4)
Введем понятие средних удельных затрат ресурса: g(
y) = х/у
.
Отношение предельных затрат ресурса к средним удовлетворяет соотношению:
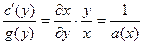 , ,
где а(х)
-
эластичность выпуска по ресурсу для f(х)
.
При выполнении предположения о том, что f''(х) <0
, получаем, что а(х) <
1
. Поэтому в таком случае предельные затраты ресурса больше средних. Для функции затрат х =
yl
/
a
,
порождаемой функцией выпуска .у = х
a
,
получаем:
 ; ; 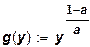 , ,
c'(
y)
 ,
,
с"(у)
 .
.
Графики перечисленных функций для функции затрат вида х =
yl
/
a
при а =
0,5
приведены на рис.1.

Рис.1.
Функция выпуска с одним продуктом и единственным ресурсом и соответствующая ей функция затрат эквивалентны: замена одной из них на другую не может привести к новым представлениям или дать преимущество при моделировании производственных единиц. Иное дело в случае нескольких ресурсов. Функция затрат для нескольких ресурсов и одного продукта имеет следующий вид:
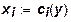 , где i = 1,..., п.
(5) , где i = 1,..., п.
(5)
Потребление каждого из ресурсов задается однозначной функцией количества выпускаемой продукции. Замещение ресурсов здесь невозможно. Ресурсы в функции затрат являются взаимодополняющими, т. е. объемы потребления ресурсов определяются жесткими технологическими условиями, и нехватка хотя бы одного из ресурсов не позволяет полностью использовать остальные ресурсы. Таким образом, описание производства с помощью функции затрат принципиально отличается от описания с помощью функции выпуска, где замещение ресурсов допустимо.
Относительно функции затрат (5) формулируются предположения, близкие по характеру к свойствам функции затрат с одним ресурсом (2). Прежде всего для простоты предполагается, что функция затрат является дважды непрерывно дифференцируемой. По аналогии с (2) считается, что, во-первых:
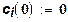 , ,
 (6)
(6)
т. е. при отсутствии производства ресурсы не нужны, и, во-вторых:
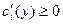 , ,  (7) (7)
т. е. рост производства требует увеличения количества используемых ресурсов.
Иногда делается следующее предположение:
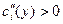 , ,  (8) (8)
т. е. предельные затраты с ростом производства растут.
Часто за счет концентрации производства имеется противоположный эффект: с ростом объема производства предельные затраты падают; в таких случаях вместо предположения (8) используется противоположное:
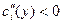 , ,  (9) (9)
означающее невозрастание предельных затрат с ростом производства.
В этом случае предельные затраты с'(у)
оказываются не больше средних, причем средние затраты также убывают с ростом выпуска продукции. Встречаются также функции затрат, для которых в некоторых диапазонах затрат выполняется соотношение (8), в других - соотношение (9). Такая ситуация может возникнуть, если при росте выпуска (у)
сначала основное влияние оказывает экономия ресурсов за счет концентрации производства, а при слишком большом выпуске эффективность начинает падать.
Билет №34
Некоторые виды функции затрат
Их 2 это линейно-однородная
и степенная
функция затрат.
Из них наиболее простая функция затрат - это линейная однородная
функция:
 ; ;  ,
(10) ,
(10)
где а
-
неотрицательный параметр.
Для этой функции выполняются предположения 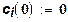 , ,
 (6)
(6)
т. е. при отсутствии производства ресурсы не нужны, и, второе: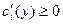 , ,  (7) (7)
т. е. рост производства требует увеличения количества используемых ресурсов.
при этом средние затраты gj
(
y)
и предельные затраты с
i
'(у)
совпадают и равны а
i
.
Близка к линейной функции затрат линейная неоднородная
функция (рис.2): ,
где di
- неотрицательный параметр. ,
где di
- неотрицательный параметр.

Рис.2
Если все di
,
= 0, то функция (11) совпадает с (10), в противном случае затраты не равны нулю даже тогда, когда продукция не выпускается. Эта функция может быть использована, когда приходится заранее делать капиталовложения, объем которых не зависит от масштабов производства. Так как для функции (11), по крайней мере для некоторых ресурсов, имеем: с
i
(0) =
di
> 0
, то предположение (6) здесь не выполняется. Поскольку 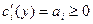 , то предположение (7) выполняется по-прежнему. , то предположение (7) выполняется по-прежнему.
При анализе функции (11) представляет интерес соотношение между предельными и средними затратами. Здесь средние затраты имеют вид:
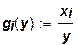  ,
поэтому ,
поэтому 
 и при
и при  и и = =

т. е. средние затраты для функции (11) превосходят предельные и стремятся к ним при стремлении выпуска к бесконечности.
Для того чтобы не нарушать предположение (6) о нулевых затратах при нулевом выпуске, иногда вместо функции (11) используют близкую к ней функцию затрат вида:
  (12) (12)
Эта функция обладает существенным недостатком: она имеет разрыв в точке 0, что затрудняет исследование моделей.
Функции (11) и (12) применяются на практике достаточно часто благодаря тому, что они хорошо выражают закономерности производства во многих экономических исследованиях.
В качестве функции затрат, характеризующейся возрастающими или убывающими предельными затратами ресурсов, можно использовать степенную функцию затрат
:
  ,
(13) ,
(13)
где а
и а - положительные параметры. Представим две такие функции в MathCADе (см. рис. 3)
Для данной функции: ; ;

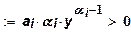
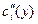
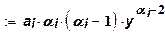

Если  , то эта функция с убывающими предельными затратами. Для нее: , то эта функция с убывающими предельными затратами. Для нее:  т.е. предельные затраты меньше средних.
т.е. предельные затраты меньше средних.
Если  , то эта функция с возрастающими затратами. Для нее: , то эта функция с возрастающими затратами. Для нее: 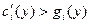 (рис.4).
(рис.4).
В зависимости от свойств моделируемой производственной единицы может быть выбрана та или иная величина  . .
В отличие от функции выпуска, которая обычно используется для описания сложных производственных единиц, функция затрат чаще всего применяется для описания производства в относительно простых экономических системах. Разнообразие производственных объектов такого типа приводит к тому, что встречается большее число различных типов функции затрат. Более того, при описании одной и той же производственной единицы могут использоваться различные функции затрат для ресурсов разных типов. Так, в некоторых моделях затраты сырьевых ресурсов выражаются линейными функциями типа (10), а затраты трудовых ресурсов и основных фондов – степенными функциями, характеризующими экономию затрат, связанную с увеличением масштабов производства.
 |
Теория предприятия часто рассматривается с позиции функции затрат, принятой в качестве первичного понятия. Такой подход значительно упрощает проведение анализа. Однако он может быть подвергнут критике с двух позиций.С одной стороны, соотношение между стоимостью затрачиваемых ресурсов и произведенным количеством зависит от цен pi
различных ресурсов, так что функция затрат изменяется при изменении этих цен. Производственная функция представляет собой, таким образом, более фундаментальное понятие, т. к. отражает технологические ограничения независимо от системы цен.
С другой стороны, теория предприятия, построенная на основе анализа затрат, плохо вписывается в теорию общего равновесия, в которой цены рассматриваются как эндогенные, а не являются определенными заранее.
|