Курсовая работа по сопротивлению материалов
"Расчёт на прочность, жёсткость и проектирование бруса в условиях сложного сопротивления статическому и динамическому нагружению"
1. Напряженное и деформированное состояние в опасной точке, проверка прочности
1.1 Определение главных напряжений в опасной точке и проверка
| σx
, МПа |
σy
, МПа |
σz
, МПа |
τxy
, МПа |
τzy
, МПа |
τxz
, МПа |
| 350 |
-310 |
420 |
0 |
350 |
100 |

Инварианты напряженного состояния по заданным компонентам
I
1
= σ
x
+σ
y
+σ
z
=460
I
2
= σ
y
ּσ
z
+σ
z
ּσ
x
+σ
x
ּσ
y
-τ
xy
2
-τ
zy
2
-τ
xz
2
= -224200
σ
x
τ
xy
τ
xz
I
3
=τ
xy
σ
y
τ
zy
= (σ
x
ּσ
y
ּσ
z
+ τ
xy
ּτ
zy
ּτ
xz
+ τ
xy
ּτ
zy
ּτ
xz
)- (τ
xz
ּσ
y
ּτ
xz
+τ
xy
ּτ
xy
ּσ
z
+τ
zy
ּτ
zy
ּσ
x
)
τ
xz
τ
zy
σ
z
=-85345000
Нахождение главных напряжений решением кубического уравнения
σ
k
3
– σ
k
2
ּI
1
+ σ
k
ּI
2
–
I
3
= 0
σ
k
3
–
σ
k
2
ּ4
60 – σ
k
ּ224200 – 85345000 = 0
Приводим уравнение к каноническому виду
q
= 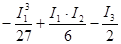 =
21878796,29
=
21878796,29
p
= 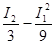 =
-98244,45 =
-98244,45
r
= 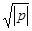 =
313,44
(
т
.
к
.
q
> 0) =
313,44
(
т
.
к
.
q
> 0)
   = = 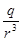 =
0,7105
=
0,7105
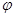 =
44,72
˚
=
44,72
˚
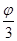 =
14,9
˚
=
14,9
˚
y
1
= 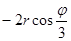 = -605,8 = -605,8
y
2
=
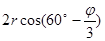 =
442,49 =
442,49
y
3
=
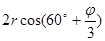 = 163,31 = 163,31
σ1
=
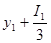 =
-452,4
=
-452,4
σ2
=
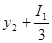 =
595,82
=
595,82
σ3
=
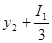 =
316,64
=
316,64
 σ1
>σ2
>σ3
σ1
=
-452,4; σ2
= 595,82; σ3
= 316,64 σ1
>σ2
>σ3
σ1
=
-452,4; σ2
= 595,82; σ3
= 316,64
Проверка
I
1г
=
σ
1
+
σ
2
+
σ
3
= 460
I
2
г
= σ1
ּσ2
+σ1
ּσ3
+σ2
ּσ3
=
-224200
I
3
г
= σ1
ּσ2
ּσ3
=
-85345000
Δ
I1
= (I1
г
– I1
)/ I1
=0
Δ
I2
= (I2
г
– I2
)/ I2
=0
Δ
I
3
= (
I
3г
–
I
3
)/
I
3
=0
1.2 Проверка прочности
Условие прочности:
n
> [
n
]
n
=
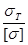 [
n
] =
[
n
] =
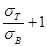
Материал 12ХН3А
σ
Т
=700 МПа
σ
В
=950 МПа
[
n
] =
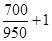 = 1,74
= 1,74
n
=
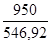 = 1,279
= 1,279
 n
< [
n
] условие прочности не выполняется. n
< [
n
] условие прочности не выполняется.
2. Компоненты тензора напряжений и проверка прочности в простейших случаях сопротивления бруса
2.1. Расчет на прочность конструкций типа кронштейнов, подвесок, валов, элементы которых работают на равномерное растяжение, сжатие
2.1.1 Силовая задача
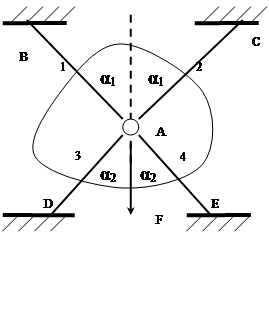
l
1
=
l
2
= 24 см
l
3
=
l
4
=31 см
A
1
=
A
2
= 2,5 см2
A3
= A4
= 2
см
2
F= 120
КН
α1
=53°
α2
=40°
Материал – 12ХНЗА
2.1.2 Определение статической неопределимости
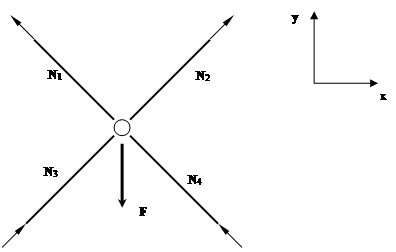
 
 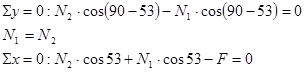 
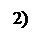
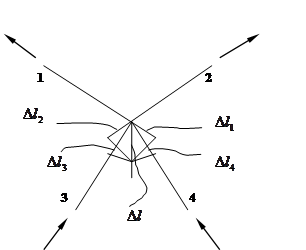

2.1.3 Уравнение деформации
Используя закон Гука имеем:
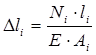 ; ;
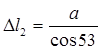 ; ; 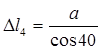
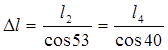
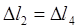
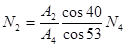
2.1.4 Определение внутренних усилий
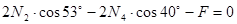 ; ;
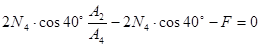 ; ;
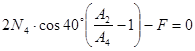 ; ;
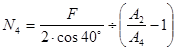 ; ;
N
4
=313,3 кН;
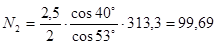 кН кН
N
1
=
N
2
= 99,69 кН
N
3
=
N
4
= 313,3 кН.
2.1.
5
Нахождение напряжений в стержнях
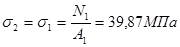 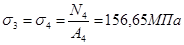
2.1.6 Проверка прочности
Условие прочности:
n
>[
n
]
n
=
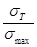 [
n
] =
[
n
] =
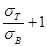
[
n
] =
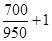 = 1,74
= 1,74
n
=
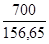 = 4,47 МПа
= 4,47 МПа
 n
> [
n
] условие прочности выполняется n
> [
n
] условие прочности выполняется
2.2 Расчет на прочность и жесткость конструкций типа валов, осей, работающих на кручение

M
1
= -30 кН·м
M
2
= -25 кН·м
M
3
= 10 кН·м
К
D
1
= 6.5
К
D
2
= 6.0
К
D
3
= 2,5
К
d
1
= 5.5
К
d
2
= 5.5
К
d
3
= 2.0
l
1
= 0,65 м;
l
2
= 0,5 м;
l
3
= 0,45 м
Материал – Ст. 45; 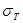 = 360МПа; = 360МПа; 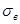 = 610 МПа;
G
= 80 ГПа = 610 МПа;
G
= 80 ГПа
2.2.1 Определение величины реактивного погонного момента
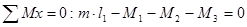 ;m ;m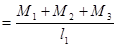 = -69,23 кН·м
= -69,23 кН·м
2.2.2 Система в данном случае статически определена
Рассмотрим 3 участка
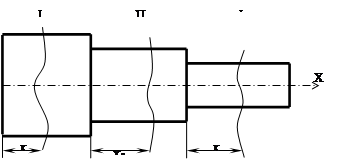
I) 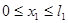
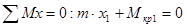
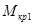 = –
m
·
x
1 = –
m
·
x
1
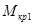 = 69,23·
x
1 = 69,23·
x
1
x
1
=0;
M
кр1
=0
x
1
=
l
1
=0.65;
M
кр1
= 45 КН·м
II
)
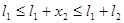
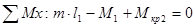
M
кр2
=
M
1
-
m
·
l
1
= -30 – (– 45) = 15 КН·м
III
)

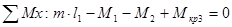
M
кр3
=
M
1
+
M
2
–
m
·
l
1
= – 30 – 25 – (-45) = -10 КН·м
2.2.3 Определение опасного сечения
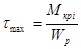 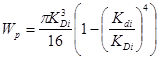
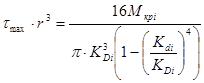
участок №1
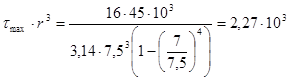
участок №2
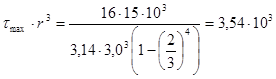
участок №3
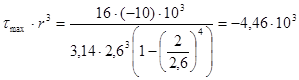
2.2.4 Определение геометрического параметра r
,
Di
и
di
из условия прочности в опасном сечении
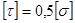
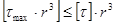
[n] = 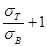 = = 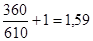
 [
σ
] = [
σ
] = 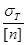 = =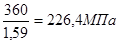 [ [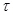 ]=113.2
МПа ]=113.2
МПа
 r3
= r3
= 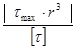 = =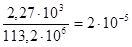 r = r = 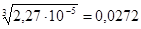
Di
= KDi
·r
D
1
= 0,204
м
D
2
= 0,0816
м
D
3
= 0,0707
м
di
=
Kdi
·к
d
1
= 0,19 м
d
2
= 0,054 м
d
3
= 0,054 м
2.2.5 Определение значений 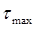 в различных сечениях бруса в различных сечениях бруса
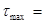
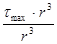
 76,4 МПа 76,4 МПа
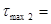 113,3 МПа 113,3 МПа
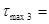 144,3 МПа 144,3 МПа
2.2.6 Определение погонного углов закручивания θ и φ

Ip1
= 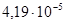 м
4
м
4
Ip2
= 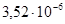 м
4
Ip3
=
м
4
Ip3
= 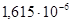 м
4
м
4
θ
1
= 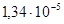 рад
/
м
рад
/
м
θ
2
= 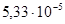 рад
/
м
рад
/
м
θ
3
= 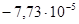 рад
/
м
рад
/
м
φ1
=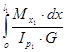 =
θ1
·
x
=
θ1
·
x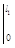 =
= 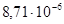
φ2
=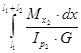 =
φ1
+θ2
·
x
=
φ1
+θ2
·
x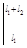 =
= 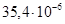
φ3
= φ2
+θ3
·
x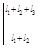 =
=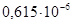
Условие жесткости по 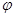
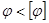 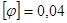
условие жесткости выполняется

3.Прочность и проектирование бруса, работающего при плоском поперечном прямом изгибе
3.1 Проектирование и расчет на прочность «оптимальной» балки с составным поперечным сечением
l
1
=
l
3
= 1,6 м
F
= 35 кН М = 60 кНм
l
2
= 1,8 м
q
= 35 кН/м

3.1.1 Построение эпюры перерезывающих (поперечных) сил и изгибающих моментов
1) 0 ≤
x
≤
l
3
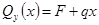
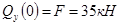
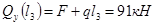
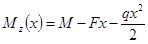
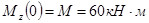
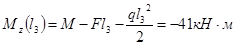
2)
l
3
≤
x
≤
l
3
+
l
2
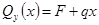
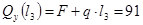 КН КН
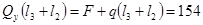 КН КН
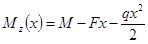
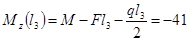 КН·м КН·м
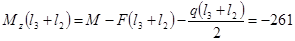 КН·м КН·м
3)
l
3
+
l
2
≤
x
≤
l
3
+
l
2
+
l
1
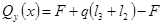
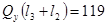 КН КН
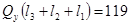 КН КН
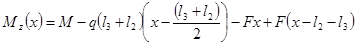
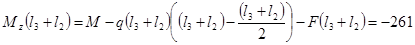 КН
·
м КН
·
м
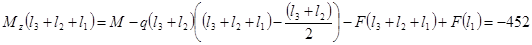 КН
·
м КН
·
м
3.2 Определение параметров поперечного сечения тонкостенной балки и полная проверка прочности
| L1
|
L2
|
L3
|
F |
q |
M |
Материал ВТ-3 |
| м |
м |
м |
кН |
кН/м |
кН·м |
σТ
= 850 МПа |
| 1,4 |
1,2 |
1,4 |
20 |
55 |
15 |
σВ
= 950 МПа |
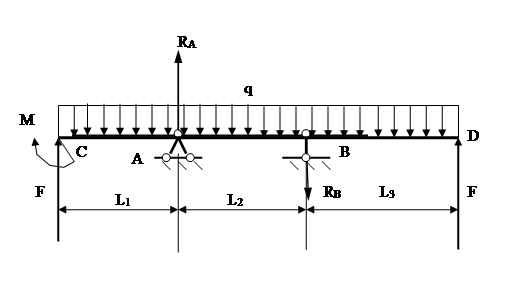
3.2.1 Определение опорных реакций
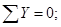 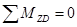
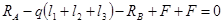
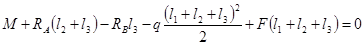
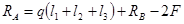
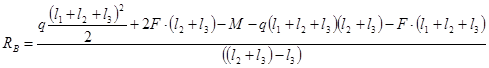
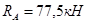
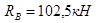
3.2.2. Построение эпюр перерезывающих сил (поперечных) и изгибающих моментов:
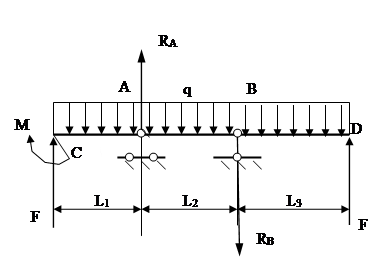
1) 0 ≤
x
≤
l
1
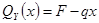
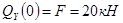
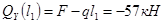
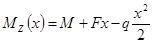
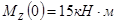
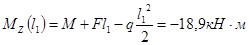
2)
l
1
≤
x
≤
l
1
+
l
2
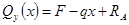
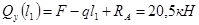

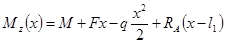
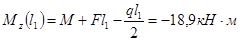
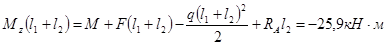
3) 0≤
x
≤
l
3
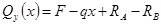
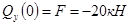
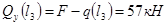
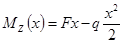
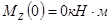
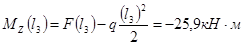
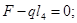
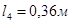
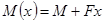
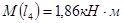
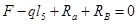
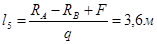
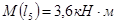
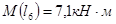
 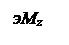
3.2.3 Определение координаты опасного сечения, как сечения, в котором изгибающий момент достигает максимальной величины
Mzmax
=25,9 КН·м в точке с координатой
x
=
l
3
– опасное сечение
3.2.4 Определение величины параметра
t из условия прочности по переменным напряжениям
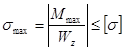
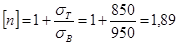
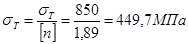
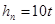
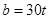
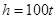
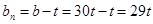
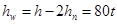
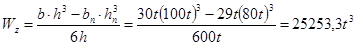
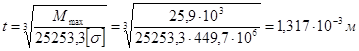
3.2.5 Определение максимального касательного напряжения в сечении, в котором перерезывающая сила достигает наибольшей величины
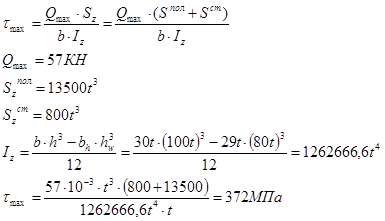
3.2.
6 Проверка прочности по касательным напряжениям
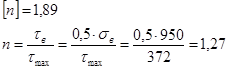
n
<[
n
] – условие прочности не выполняется
3.2.7 Построение эпюры нормальных и касательных напряжений по высоте сечения, в котором изгибающий момент достигает максимальной величины
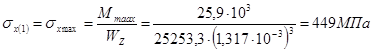
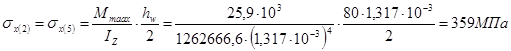
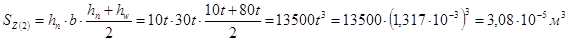
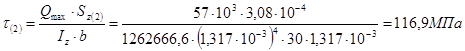
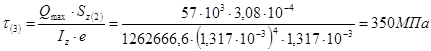
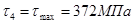
3.2.8 Определение главных, эквивалентных напряжений и построение эпюры эквивалентных напряжений по высоте сечения; определение опасной точки сечения
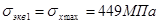
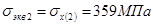
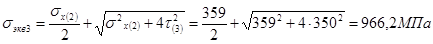
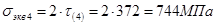
3.2.9 Проверка прочности балки
n
=
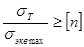
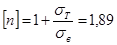
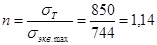
n
> [
n
] условие прочности не выполняется
Список использованной литературы
1. Беляев Н.М. Сопротивление материалов. М: Наука, 1976
2. Копнов В.А. Сопротивление материалов. М: Высш. Шк., 2003
3. Писаренко Г.С. и др. Справочник по сопротивлению материалов. 1975
4. Феодосьев В.И. Сопротивление материалов. М: Наука, 1974
|