| Томский межвузовский центр дистанционного образования
Томский государственный университет
систем управления и радиоэлектроники (ТУСУР)
Контрольная работа № 1
по дисциплине
«Математическая логика и теория алгоритмов»
автор учебного пособия:
Зюзьков В.М.
Выполнил:
Студент ТМЦДО
специальности 220201
Вариант №11
1) Перевести на формальный язык (обязательно указывая универсум):
«Некоторые лентяи на оптимисты, но жизнелюбы».
Универсум М ={люди}. Предикаты: L(x) ≡ «х – лентяй», O(x) ≡ «х – оптимист», Z(x) ≡ «х – жизнелюб».
Формула: 
2) Перевести на формальный язык (обязательно указывая универсум):
«Два философа сидят за столом и спорят»
Универсум М ={люди}. Предикаты: F(x) ≡ «х – философ», S(x) ≡ «х – сидит за столом», С(x,y) ≡ «х спорит с y»
Формула: 
3) Перевести с формального языка на человеческий:
(R – Множество вещественных чисел).
Перевод: Для любого вещественного числа есть большее, синус которого равен нулю.
4) Перевести на формальный язык (обязательно указывая универсум):
«Ни один судья не справедлив».
Универсум М ={люди}. Предикаты: J(x) ≡ «х – судья», S(x) ≡ «х – справедлив».
Формула: 
5) Является ли формула
 тавтологией?
Использовать метод доказательства от противного.
Тавтология – формула, истинная независимо от того какие значения принимают переменные входящие в неё. Соответственно нам необходимо доказать, что она не может быть ложной. Представим, что формула ложна при некотором сочетании переменных.
| 
|
| 
|
|
| 
|
|
|  (подставили в формулы значения q, r и t )
|
| Желая избежать противоречия  примем  , получим 
|
|  , противоречия нет.
|
Получили значения переменных,  при которых формула является ложной, следовательно, она опровержима и не является
тавтологией
.
6) При каких значениях переменных формула
 ложна?
 
Переберём все возможные комбинации.
1. Из утверждения  получаем, что  и одновременно  невозможно.
2. Из утверждения  получаем, что  и одновременно  невозможно
3. Из утверждения  получаем, что и одновременно невозможно
4. Возьмём и , получаем  (верно),  (верно),  (верно).
 выполняется.
Ответ: формула ложна только при и , других вариантов нет.
7) Является ли формула
 тавтологией?
| 
|
| 
|
|
| 
|
|
|  (подставили в формулы значения Л, r и t )
|
| Так как  и  , то  подставим и получим
|
|  - противоречие.
|
Пришли к противоречию, следовательно, исходная формула – тавтология.
8) Проверить, что  и 
Решение: Сначала следует попробовать опровергнуть это утверждение, т.е. найти такие множества A,
B
и C
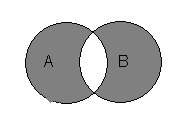
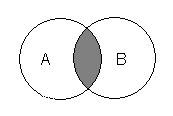
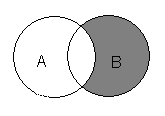
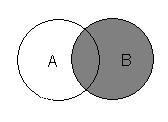
, чтобы выполнялось отношение  , но не выполнялось  и или, наоборот, выполнялось и , но не выполнялось . После безуспешных попыток найти такие множества следует доказать данное утверждение.
Доказательство распадается на два этапа.
1. Докажем сначала, что и  . Пусть и выполнено, докажем, что . Поскольку требуется доказать включение множеств, то возьмем произвольный элемент  , следовательно  (из ), значит  и тем более . Аналогично для  .
2. Докажем теперь, что и . Пусть выполнено, докажем, что и . Поскольку требуется доказать включение множеств, то возьмем произвольный элемент , однозначно . Значит  и тогда  . Аналогично для B
. Доказательство закончено.
9) Проверить, что 
Это выражение верно, так как согласно  не существует элемента , который не входил бы в  . Следовательно, для  ,  . Обратное не верно.
10) Проверить тождество 
Решение. Построим диаграмму Эйлера для левого множества в четыре этапа.
| Диаграмма для множества 
|
Диаграмма для множества 
|
| 
|
|
| Диаграмма для множества 
|
Диаграмма для множества 
|
| 
|
|
Диаграммы Эйлера показывают, что тождество выполняется. Докажем это. Используя основные тождества алгебры множеств, преобразуем левую и правую части к одному множеству.
 
 
Преобразуем отдельно первое и второе множества.
 
|