Тема: Расчет характеристик системы передачи дискретных сообщений
Исходные данные:
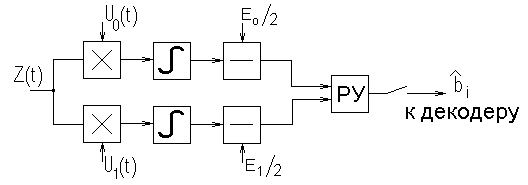
Структурная схема системы передачи дискретных сообщений:

ИС – источник сообщения; Д – дискретизатор; К – кодер; ЛС – линия связи; ДМ – демодулятор; ДК – декодер; Ф – фильтр-восстановитель.
Исходные данные
| amin
,В |
amax
,В |
Fc
, Гц |
j |
Вид. мод |
N0
, В2
/Гц |
| 0
|
25,6
|
106
|
198
|
ФМ
|
10-8
|
Способ приема - когерентный.
Источник сообщений.
Источник сообщений выдает сообщение а(t), представляющее собой непрерывный стационарный случайный процесс, мгновенные значения которого в интервале а min
 amax
распределены равномерно, а мощность сосредоточена в полосе частот от 0 до Fc
. amax
распределены равномерно, а мощность сосредоточена в полосе частот от 0 до Fc
.
Требуется:
1.  Записать аналитические выражения и построить график одномерной плотности вероятности мгновенных значений сообщения а(t). Записать аналитические выражения и построить график одномерной плотности вероятности мгновенных значений сообщения а(t).
2. Найти мат. ожидание и дисперсию сообщения а(t)
3. Построить график случайного процесса и на графике обозначить max значение сигнала, математическое ожидание и среднеквадратичное отклонение.
Вычисления.
1) 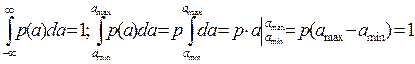
 =0.0390625 =0.0390625

2)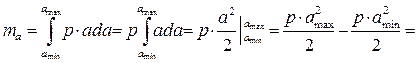

σа
= 14.78 В
Дискретизатор.
Передача непрерывного процесса осуществляется дискретными методами. Для этого сообщение а(t) дискретизируется по времени и квантуется по уровню с равномерным шагом. Шаг квантования по уровню Dа= 0,1В.
Требуется:
1. Определить шаг дискретизации по времени (Dt).
2. Определить число уровней квантования (L).
3. Рассчитать среднюю мощность шума квантования.
4. Рассматривая дискретизатор как источник дискретного сообщения с объемом алфавита L, определить его энтропию и производительность (Н, Н’
), отсчеты, взятые через интервал Dt считать независимыми.
Вычисления.
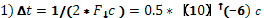

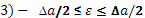
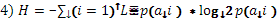
Т.к. p(a1
)= p(a2
)=…= p(ai
), то 
Следовательно бит/символ бит/символ

Кодер.
Кодирование осуществляется в два этапа.
Первый этап:
Производится примитивное кодирование каждого уровня квантованного сообщения k
– разрядным двоичным кодом.
Второй этап:
К полученной k
– разрядной двоичной кодовой комбинации добавляется один проверочный символ, формируемый простым суммированием по модулю 2 всех информационных символов (код (n,
n
-1) с одной проверкой на четность).
В результате этих преобразований на выходе кодера образуется синхронная двоичная случайная последовательность b(
t)
(синхронный случайный телеграфный сигнал), состоящая из последовательности биполярных импульсов единичной высоты, причем положительные импульсы в ней соответствуют символу «0», а отрицательные – символу «1» кодовой комбинации.
Требуется:
1. Определить число разрядов кодовой комбинации примитивного кода k
, необходимое для кодирования всехL
уровней квантованного сообщения.
2. Определить избыточность кода с одной проверкой на четность.
3. Записать двоичную кодовую комбинацию, соответствующую передачеj
-го уровня, считая, что при примитивном кодировании на первом этапеj
-му уровню ставится в соответствии двоичная кодовая комбинация, представляющая собой запись числаj
в двоичной системе счисления. В полученной кодовой комбинации указать информационные и проверочные разряды.
4. Определить число двоичных символов, выдаваемых кодером в единицу времени Vn
и длительность двоичного символа T
.
Вычисления.

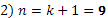

3) j=198. В двоичном виде-
| 0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
| a8
|
a7
|
a6
|
а5
|
а4
|
а3
|
а2
|
а1
|
проверочный разряд а9
= а8
+а7
+ а6
+ а5
+ а4
+ а3
+ а2
+ а1
В результате получаем кодовую комбинацию: 110001100;
4) Vn
= n/∆
t
=9/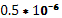 =18·106
бит/с; =18·106
бит/с;
T
= 1/Vn
=5.5.
10-8
с.
Модулятор.
В модуляторе синхронная двоичная случайная последовательность биполярных импульсов b(
t)
осуществляет модуляцию гармонического переносчика Um
= cos(
2π
ft).
Фазовая модуляция (ФМ).
«0» - U0
(
t)
= Um
cos2π
ft
;
«1» - U1
(
t)
= -Um
cos2π
ft
.
Требуется:
1. Записать аналитическое выражение модулированного сигнала U(
t)=φ(
b(
t)).
2. Изобразить временные диаграммы модулирующего b(
t)
и модулированного U(
t)
сигналов, соответствующие передачи j
-го уровня сообщения a(
t).
3. Привести выражение и начертить график корреляционной функции модулирующего сигнала В(τ).
4. Привести выражение и начертить график спектральной плотности мощности модулирующего сигнала GВ
(ω).
5. Определить ширину энергетического спектра модулирующего сигнала ∆
FB
из условия ∆
FB
=α
Vk
(где α выбирается в пределах от 1 до 3). Отложить полученное значение ∆
FB
на графике GВ
(ω).
6. Привести выражение и построить график энергетического спектра G
U
(ω)
модулированного сигнала. (В случае ЧМ частоты сигналов U0
(
t)
и U1
(
t)
выбирать из условия их ортогональности на интервале Т
).
7. Определить ширину энергетического спектра ∆
Fu
модулированного сигнала и отложить значение ∆
Fu
на графике G
u
(ω).
Вычисления

 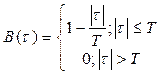
 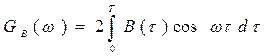
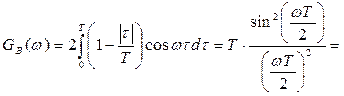

График спектральной плотности мощности модулирующего сигнала GВ
(
w)
:

При увеличении  на один порядок мы наблюдаем следующую картину: на один порядок мы наблюдаем следующую картину:


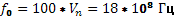 ; ∆f
=2/T
=2/5.5.
10-8
=35·106
Гц ; ; ∆f
=2/T
=2/5.5.
10-8
=35·106
Гц ;
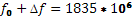 Гц; Гц; 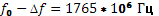
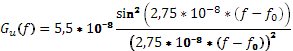
При ФМ:
U0
(t)
= cos(2π
f0
t)
= cos(
U1
(t)
= cos(2π
f0
t+π
)
=- cos

 Гц Гц
Канал связи.
Передача сигнала U(
t)
осуществляется по каналу с постоянными параметрами и аддитивным флуктуационным шумом n(t) с равномерным энергетическим спектром N0
/2 (белый шум).
Сигнал на выходе такого канала можно записать следующем образом:
z(
t) =
U(
t) +
n(
t)
Требуется:
1. Определить мощность шума в полосе частот Fk
= ∆
Fu
;
2. Найти отношение сигнал – шум Рс
/Рш
;
3. Найти пропускную способность канала С
;
4. Определить эффективность использования пропускной способности канала Кс
, определив ее как отношение производительности источника Н’
к пропускной способности канала С
.
Вычисления.
 Вт Вт
 , где , где 
 ; ;
Так как
 ; ;

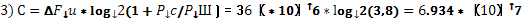

Демодулятор.
В демодуляторе осуществляется оптимальная когерентная или некогерентная (в зависимости от варианта) обработка принимаемого сигнала z(
t) =
U(
t) +
n(
t)
Требуется:
Записать алгоритм оптимального приема по критерию минимума средней вероятности ошибки при равновероятных символах в детерминированном канале с белым гауссовским шумом.
1. Нарисовать структурную схему оптимального демодулятора для заданного вида модуляции и способа приема.
2. Вычислить вероятность ошибки ρ
оптимального демодулятора.
3. Определить, как нужно изменить энергию сигнала, чтобы при других видах модуляции и заданном способе приема обеспечить найденное значение вероятности ошибки ρ
.
Вычисления.
1)
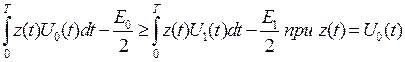
Для фазовой модуляции Е0
/2 = Е1
/2, U1
= –
U0
, следовательно:


 2) 2)
3) P = 1/2 (1-Ф(х));
Ф(х) – функция Крампа
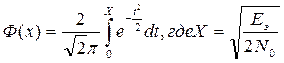
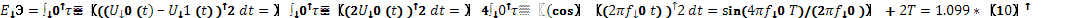 Дж Дж
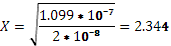

4. При когерентном приёме вероятность ошибки при АМ, ЧМ, ФМ определяется соотношением 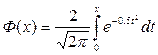 , которое зависит от x.
х-
определяется из энергии сигнала, значит энергию измерять не надо, т.к. при других видах модуляции вероятность ошибки остаётся той же. ФМ обеспечивает наибольшую помехоустойчивость. Энергетический выигрыш её составляет в четыре раза по сравнению с АМ и в два раза по сравнению с ЧМ. , которое зависит от x.
х-
определяется из энергии сигнала, значит энергию измерять не надо, т.к. при других видах модуляции вероятность ошибки остаётся той же. ФМ обеспечивает наибольшую помехоустойчивость. Энергетический выигрыш её составляет в четыре раза по сравнению с АМ и в два раза по сравнению с ЧМ.
Декодер.
В декодере декодирование осуществляется в два этапа. На первом этапе производится обнаружение ошибок в кодовой комбинации. Если ошибки не обнаружены, то на втором этапе из нее выделяются информационные символы, а затем k – разрядная двоичная кодовая комбинация преобразуется в элемент квантованного сообщения.
Требуется:
1. Оценить обнаруживающую способность q
кода (n,
n
-1) с одной проверкой на четность.
2. Записать алгоритм обнаружения ошибок.
3. Определить вероятность не обнаружения ошибки.
Вычисления.
1) dmin
= 2;
q =
dmin
–1 = 1
2) Кодовая последовательность:11000110
Если b
9
=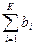 то, ошибки нет. то, ошибки нет.
Если b
9
≠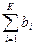 то, ошибка есть. то, ошибка есть.
3)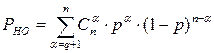
n
– число разрядов, n
= 9
р
– вероятность ошибки в одном разряде, p = 


Фильтр – восстановитель.
Фильтр–восстановитель представляет собой фильтр нижних частот с частотой среза Fc
.
Требуется:
1. Указать величину Fc
.
2. Изобразить идеальные АЧХ и ФЧХ фильтра – восстановителя.
3. Найти импульсную характеристику g
(
t
)
идеального фильтра – восстановителя и начертить ее график.
Вычисления.
1) Fc
= 106
Гц;
w
ср
=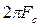 =2·π·106
=6,28·106 =2·π·106
=6,28·106
2) Идеальная АЧХ фильтра – восстановителя имеет вид:
 Идеальная ФЧХ:
 3)


Так выглядит этот график при увеличении
tна 2 порядка:

При увеличении на 3 порядка:

При увеличении на 7 порядков:

|