Федеральное агентство по образованию

Вступительный реферат в аспирантуру на тему:

«ПОСТРОЕНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ, РЕАЛИЗАЦИЯ ИХ НА ЭВМ ДЛЯ ИССЛЕДОВАНИЯ ФИЗИЧЕСКИХ ЯВЛЕНИЙ»
(на примерах в нефтедобыче, томографии, строении вещества)

Специальность: 05.13.18 – «Математическое моделирование,
численные методы и комплексы программ»

Выполнила:
Габидинова Айгуль Ринатовна.

Казань – 2006

ОГЛАВЛЕНИЕ

Введение... 3

Подходы и методы.... 4

Моделирование в нефтедобыче... 7

Управление нефтедобывающим производством... 7

Постановка задачи.. 8

Реализация.. 8

Пример процесса оптимизации.. 9

Полученные результаты... 12

Заключение.. 12

моделирование в МЕДИЦИНСКой физике... 13

Диагностика онкологических заболеваний.. 13

Постановка задачи.. 14

Реализация.. 15

Виды обмена данных с устройствами.. 17

Организация класса работы с устройствами.. 18

Программная часть. 19

Пользовательский интерфейс. 21

Результаты работы программы... 22

Заключение.. 24

Моделирование строения атома... 25

Движение электрона в кулоновском поле ядра.. 25

Постановка задачи.. 26

Вывод алгоритма.. 28

Полученные результаты... 30

Литературный обзор.. 32

Введение

Прикладная математика является областью математики, представляющей собой научный инструмент для создания математических моделей объектов, систем, процессов и технологий, предназначенных для проведения расчетов, анализа, подготовки решений и разработки наукоемкого программного обеспечения во всех сферах производственной, хозяйственной, экономической, социальной, управленческой деятельности, в науке, технике, медицине, образовании.

Мои научные интересы это компьютерное моделирование физических процессов в таких прикладных областях математики как физика, электроника, медицина. Изучение физических явлений с помощью математического моделирования является признанным, быстро развивающимся и перспективным направлением в науке и технике.

Цель подобной работы для существующей задачи описать модель и применив численные методы написать программу, с помощью которой будут получены результаты для анализа, прогнозирования и выбора оптимальных решений.

Такая диссертационная работа может стать продолжением научных исследований, проводимых мною во время обучения на ВМК КГУ. Приобретенная теоретическая база и навыки, научные интересы и достижения соответствуют специальности аспирантуры.

Имеется опыт моделирования различных физических процессов (движение электрона в кулоновском поле ядра, магнитно-резонансная томография, производство нефти). На основе таких моделей с помощью самостоятельно разработанных программ были получены практические результаты. Проделанные работы были оценены на отлично и имели практическое применение.

Подходы и методы

Современные исследования настолько наукоёмки, что просто физически невозможно обойтись без помощи вычислительной машины. Колоссальные объёмы информации требуется анализировать при исследовании процессов в различных областях науки и техники. Автоматизация исследований невозможна без описания математической модели процесса и применения численных методов. Математическая модель - это система математических соотношений, приближенно, в абстрактной форме описывающих изучаемый процесс или систему. Математическое моделирование необходимо для эффективного изучения любых процессов. В настоящее время математические модели применяются для анализа, прогнозирования и выбора оптимальных решений.

Прогнозирование глобальных процессов необходимо для человечества - исследование космоса, исследование протекающих в земной коре процессов, прогнозирование землетрясений, прогнозирование погоды, исследование глобальных изменений климата, внедрение новых экозащитных технологий, разработка энергосберегающих систем и т.п.

Планирование и оперативное управление производством применяется во всех областях экономики: управление трудовыми ресурсами, управление запасами, распределение ресурсов, планировка и размещение объектов, руководство проектом, распределение инвестиций и т.п.

Исследуются всевозможные процессы в теплоэнергетике - горение топлива в различных моделях топок, течение парожидкостных смесей в проточных частях турбогенераторов (расчёт нагрева металла и его расширение при различных граничных условиях, основывается на решении уравнений теплопроводности) и расплавленных металлов, являющихся теплоносителем первого контура, в парогенераторах атомных электрических станций, исследуется влияние струй пара на поверхность лопаток турбины, что необходимо для предотвращения их коррозионного износа, так же исследуются процессы протекания ядерных реакций в тепловыделяющих элементах (ТВЭЛах). Большинство процессов в теплоэнергетике уже давно изучено. Исследования проходят по оптимизации этих процессов и изучению глубинной сути явлений для достижения максимального эффекта при разработке энергетического оборудования. Здесь и нужна математическая модель.

Хорошую модель составить не просто. Известный математик Р.Беллман сказал так: «Если мы попытаемся включить в нашу модель слишком много черт действительности, то захлебнемся в сложных уравнениях; если слишком упростим ее, то она перестанет удовлетворять нашим требованиям». Для успешного моделирования необходимо учесть главные свойства моделируемого объекта, пренебрегать его второстепенными свойствами, уметь отделить главные свойства от второстепенных.

Можно выделить следующие основные этапы операционного исследования :

· наблюдение явления и сбор исходных данных;

· постановка задачи;

· построение математической модели;

· расчет модели;

· тестирование модели и анализ выходных данных. Если полученные результаты не удовлетворяют исследователя, то следует либо вернуться на этап 3, т.e. предложить для решения задачи другую математическую модель; либо вернуться на этап 2, т.e. поставить задачу более корректно;

· применение результатов исследований.

Таким образом, операционное исследование является итерационным процессом, каждый следующий шаг которого приближает исследователя к решению стоящей перед ним проблемы. В центре операционного исследования находятся построение и расчет математической модели.

Найдя частное решение уравнения для линейной модели, с помощью принципа суперпозиции можно получить решение в общем случае. Однако, многие модели реальных процессов оказываются нелинейными. Принцип суперпозиции здесь неприменим, и алгоритмов для построения общего решения не существует. Поэтому для нелинейных моделей законченных теоретических результатов получено немного.

Методология математического моделирования в кратком виде выражена знаменитой триадой "модель - алгоритм - программа", сформулированной академиком А. А. Самарским, основоположником отечественного математического моделирования. Эта методология получила свое развитие в виде технологии "вычислительного эксперимента", разработанной школой А. А. Самарского, - одной из информационных технологий, предназначенной для изучения явлений окружающего мира, когда натурный эксперимент оказывается слишком дорогим и сложным.

Во многих важных областях исследований натурный эксперимент невозможен, потому что он либо запрещен (например, при изучении здоровья человека), либо слишком опасен (например, при изучении экологических явлений), либо просто неосуществим (например, при изучении астрофизических явлений).

Моделирование в нефтедобыче

Основной задачей нефтедобывающих предприятий является добыча, начальная переработка и продажа нефти. Для ее выполнения необходимо множество вспомогательных производств, предназначенных для создания и поддержки необходимой инфраструктуры.

На основе математического моделирования создаются трехмерных числовые геолого-технологические модели месторождений. Анализируются разработки и выработки запасов нефти, а так же эффективность применения способов добычи. Разрабатываются программные комплексы для анализа и интерпретации данных исследований скважин, а так же для нахождения способов повышения нефтеотдачи пластов.

Управление нефтедобывающим производством

Управление нефтедобывающим производством является очень сложной задачей из-за необходимости интеграции и взаимного согласования деятельности множества организаций и подразделений, принятия решения в условиях многих неопределенностей, связанных с часто недостаточными знаниями о процессах, происходящих в недрах. В этих условиях предприятие не может обойтись без специализированных средств, осуществляющих информационную поддержку принятия решений, повышающих эффективность работы предметных специалистов, приводящих к более оптимальным решениям по управлению.

От функционирования информационной системы (ИС) компании напрямую зависит эффективность работы самой компании, и как следствие, её конкурентоспособность. Компаний, в производственном процессе которых используются значительные объемы данных, в наше время становится все больше. Одной из них является ОАО «Татнефть», где проводилась моя дипломная работа.

Постановка задачи

Даже с успешно введенным в эксплуатацию приложением со временем возникают проблемы производительности, так как меняется сама система: происходит рост хранимой информации, появляются новые пользователи, изменяется состав данных. Поэтому, чтобы не допустить ухудшения характеристик как отдельных приложений, так и всей системы в целом, требуется исследование ИС и использование специальных методов, повышающих скорость доступа к данным. Управление большими и сверхбольшими базами данных, проектирование и разработка приложений для них имеет свои особенности.

Задачей дипломной работы являлось определение возможных действий, необходимых при решении типовых проблем производительности серверов Oracle, не изменяющих бизнес-логику и структуру SQL-запроса, так как для эксплуатирующихся систем это, как правило, невозможно.

Реализация

Основные технологические системы «Татнефть» это OilServer - информационно-аналитический комплекс управления нефтедобывающим производством. Это самая большая БД «Татнефти». В её состав входит более 450 таблиц. Объем хранящейся в ней информации занимает около 40Гб. Энергосервер – это прикладная система, предназначенная для информационного обеспечения процессов, связанных с энергоснабжением. В её состав входит более 150 таблиц. Объем хранящейся в ней информации занимает около 20Гб.

Средства Oracle для оптимизации производительности

Пример процесса оптимизации

1) Процесс установки пакета StatsPack

С:\oracle\RDBMS\ADMIN>sqlplusinternal

SQL*PLUS: Release 8.1.6.0.0 - ProductiononSunMar18 11:52:32 2001

(c) Copyright 1999 Oracle Corporation. All rights reserved.

Connected to:

Orade8i Enterprise Edition Release 8.1.6.0.0 – Production

With the Partitioning option

JServer Release 8.1.6.0.0 – Production

sya@TKYTE816> @statsere

... Installing Required Packages

2) Организация сбора статистической информации каждые 10 минут

3) Выявленный в отчете StatsPack ресурсоемкий запрос

CPU Elapsd

Buffer Gets Executions Gets per Exec %Total Time(s) Time(s) Hash Value

----------------------------------------------------------------------------

334,030 1 334,030.0 0.4 55.33 90.89 2322365808

Module: C:\PROGRA~1\MICROS~1\MSSQL\binn\sqlservr.exe

select substr(b.источник,instr(b.источник,'КНС',1,1)+3,instr(b.и

сточник,',',1,1)-instr(b.источник,'КНС',1,1)-3) as kns, substr(

b.источник,instr(b.источник,'НА',1,1)+2,instr(b.источник,',',1,2

)-instr(b.источник,'НА',1,1)-2) as na, b.значение_сигнала as ra

b,b.кон_дата as dat from telemetry.события_телеметрии b where

b.КОН_ДАТА>to_date('30/12/2005 15:33:41','DD/MM/YYYY HH24:MI:SS'

) and b.КОН_ДАТА<trunc(sysdate,'HH24') and SUBSTR(b.источник,1,

5)='А КНС' and SUBSTR(b.тг_наименование,22,5)='NAON_' and b.знач

ение_сигнала in (1,0) orderbyb.тг_наименование,b.источник,b.

КОН_ДАТА

4) Запрос после форматирования

SELECT SUBSTR(b.источник, INSTR(b.источник, 'КНС', 1, 1) + 3, INSTR(b.источник,

',', 1, 1) - INSTR(b.источник, 'КНС', 1, 1) - 3) kns, SUBSTR(b.источник,

INSTR(b.источник, 'НА', 1, 1) + 2, INSTR(b.источник, ',', 1, 2) -

INSTR(b.источник, 'НА', 1, 1) - 2) na, b.значение_сигнала rab, b.

кон_дата dat

FROMtelemetry.события_телеметрии b

WHERE b.кон_дата > TO_DATE('30/12/2005 15:42:29', 'DD/MM/YYYY HH24:MI:SS')

AND b.кон_дата < TRUNC(SYSDATE, 'HH24')

AND (SUBSTR(b.источник, 1, 6) = 'Аз КНС'

OR SUBSTR(b.источник, 1, 6) = 'Ак КНС')

AND SUBSTR(b.тг_наименование, 22, 5) = 'NAON_'

ANDb.значение_сигнала IN (1, 0)

ORDERBYb.тг_наименование, b.источник, b.кон_дата

5) Разбор запроса в Explain Plan

6) Создание функционального индекса

CREATE INDEX "TELEMETRY"."I1_TEL"

ON "TELEMETRY"."СОБЫТИЯ_ТЕЛЕМЕТРИИ" (SUBSTR(источник, 1, 6),

SUBSTR(тг_наименование, 22, 5), "КОН_ДАТА")

Обновлениестатистикииндекса:analyze index I1_TEL compute statistics

7) Проверка результативности в ExplainPlan

Вывод: в результате произведенных действий стоимостная оценка запроса (Cost) уменьшилась с 58095 до 7.

Полученные результаты

Всего была собрана информация об около 600 запросах, из них было отобрано 9 и оптимизировано 5. Наряду с разобранным примером был создан эффективный Bitmap-индекс к другой таблице - время выполнения проблемного запроса сократилось более чем в 40 раз. Результатом изменения ключевых подсказок стало ускорение выполнения запроса более чем в 13 раз. Помимо этого на системах Татнефти были оптимизированы настройки параметров памяти, выявлены неселективные запросы и жесткие разборы и минимизировано их количество. Но все же наибольшую результативность в повышении производительности показала работа с индексами.

Заключение

Была изучена проблема производительности этих БД и разработана методика оптимизации производительности серверов Oracle, а затем применена к базам данных ОАО «Татнефть», благодаря чему существенно ускорилась работа некоторых запросов.

Значительной пользой является то, что разработанная методика может быть успешно применена для оптимизации любых информационных систем на базе ORACLE.

моделирование в МЕДИЦИНСКой физике

Одним из перспективных направлений изучения физиологии и патофизиологии сложных физиологических систем организма человека является математическое моделирование. Математическая модель несет в себе знания о закономерностях взаимодействия отдельных звеньев сложной системы и позволяет исследовать поведение сложной физиологической системы при патологических нарушениях отдельных ее звеньев.

Медицинская кибернетика - научное направление, связанное с проникновением идей, методов и технических средств кибернетики в медицину. Развитие идей и методов кибернетики в медицине осуществляется в основном в направлениях создания диагностических систем для различных классов заболеваний с использованием универсальных или специализированных ЭВМ; создания автоматизированного электронного медицинского архива; разработки математических методов анализа данных обследования больного; разработки метода математического моделирования на ЭВМ деятельности различных функциональных систем; использования математических машин для оценки состояния больного.

Диагностика онкологических заболеваний

Ключевое значение для медицины имеет диагностика. Диагностика онкологических заболеваний осуществляется с применением математических методов описания и анализа сложных явлений при помощи вычислительных систем с применением современных методов магнитно-резонансной спектроскопии и фундаментальными знаниями о метаболизме (его регуляции).

Магнитно-резонансная томография (МРТ) - это метод отображения, используемый для получения высококачественных изображений органов человеческого тела. МРТ основана на принципах ядерно-магнитного резонанса (ЯМР), методе спектроскопии, используемом учеными для получения данных о химических и физических свойствах молекул. МРТ находит все более широкое применение в медицинской практике и отличается от других методов высоким контрастом мягких тканей и безопасностью воздействия на организм человека.

В лаборатории методов медицинской физики КФТИ КНЦ РАН им. Е.К.Завойского разрабатываются, изготавливаются и запускаются в эксплуатацию медицинские магнитно-резонансные томографы "ТМР-КФТИ", которые предназначены для диагностики патологий головного мозга, позвоночника и суставов.

Постановка задачи

Важным этапом в процессе производства является диагностика и проверка работоспособности изготовленных приборов. Мною была разработана система, тестирующая блок радиоэлектроники МР-томографа – спектрометр . Система реализована средствами Visual C++ (MFC). Сопряжение спектрометра с ПК происходит через параллельный интерфейс XB (на плате ISA). В программном комплексе реализована работа с портами ввода/вывода, используются несколько видов обмена данных с устройствами (через драйверы нижнего, верхнего уровня), различные алгоритмы тестирования, уровни доступа в зависимости от используемой ОС. Применяются Grid, CtrlTab, drivers, threads, I/O ports; представление чисел в Hex Dec Bin. Организован класс работы с устройствами.

Реализация

Рисунок 1. Схема основных частей спектрометра

Плата интерфейса использует часть пространства ввода/вывода ЦП. Адресное пространство расположено в диапазоне адресов 0x300-0х31F (64 порта).

Адресное пространство интерфейса распределено между устройствами спектрометра. Для операций ввода/вывода устройства отображают на шину по два регистра (по 16bit): регистр данных (data reg) и регистр команд (cmd reg).

Так, например, операция записи слова выглядит следующим образом:

1. Запись в регистр команд кода команды записи;

2. Запись в регистр данных слова;

После выполнения второго шага произойдет запись слова в ячейку памяти с адресом, указанным в адресном счетчике.

Рисунок 2. Адресное пространство ввода/вывода ЦП

Рисунок 3 . Адресное пространство устройства

Виды обмена данных с устройствами

Существуют команды процессора in и out, которые осуществляют чтение и запись в порт ввода/вывода. С помощью этих команд осуществляется ввод/вывод с устройствами спектрометра. Однако исполнять их из пользовательского уровня («напрямую») разрешено далеко не во всех операционных системах (ОС), например, в WinNT/XP. Помимо этого в многозадачных ОС возможны критические ситуации, когда параллельно выполняются неатомарные операции (подоперации которых разнесены во времени, в течение которого может выполниться операция другого процесса) с одним устройством, что может привести к неверным и неожиданным результатам. Во избежание этого специалистами лаборатории ММФ КазНЦ был разработан драйвер нижнего уровня .

Для абстрагирования программного обеспечения прикладного уровня от аппаратной части в лаборатории так же был разработан набор драйверов верхнего уровня.

Использование драйверов нижнего и верхнего уровня в данной работе позволяет диагностировать спектрометр на ПК с различными ОС.

Сопровождение развивающейся аппаратной части МР-томографа влечет необходимость модификации драйверов. Одной из возможностей программы является диагностика новых версий драйверов (с помощью разных уровней доступа).

Пример использования уровней доступа для записи данных в устройство

Доступ « Напрямую » ( для Win9X)

void CHardWare::dioWrite(WORD adr,WORD val)

{//запись через порты (W9X) слова val в регистр устройства с адресом adr

adr+=DEFAULT_IO_BASE; //Переход к адресному пространству интерфейса

__asm{

movdx,adr //Запись в регистр dx адреса

movax,val //Запись в регистр ax значения

outdx,ax //Выполнение команды записи в порт

}

}

Доступ с использованием драйвера низкого уровня

void CHardWare::OUTWORD(WORD adr,WORD val)

{

fxbOutWord(IOSession,adr,val,0xffff); //враппер функции записи слова в драйвере низкого уровня

}

Доступ с использованием драйвера высокого уровня

int CHardWare::WriteBuf(UINT ndev,PWORD buf,int len)

{

switch(ndev)

{

case CH_SYN:

fnmrtResetSynth(0);

fnmrtLoadSynth((XBPInt16)buf,len,0,0);

break;

case CH_PPU:

fnmrtStopPPU();

fnmrtResetPPU(0);

fnmrtLoadPPUCode(buf,len,0,0);

break;

case CH_GX:

case CH_GY:

case CH_GZ:

case CH_RFP:

fnmrtLoadGradChannel(ndev+1,(XBPInt16)buf,len,0,0);

break;

default:

return -1;

}

return 0;

}

Организация класса работы с устройствами

Для работы с устройствами был разработан отдельный класс – CHardWare . В связи с имеющимися различными уровнями доступа для удобства было разработано три уровня абстракции работы с устройствами.

1. Ввод/вывод слов в регистры устройств

2. Ввод/вывод команд и данных в память устройств спектрометра

3. Ввод/вывод массивов в память устройств

Пример использования различных уровней абстракции для записи данных в устройство

1. Ввод/вывод слов в регистры устройств

void CHardWare::OUTWORD(WORD adr,WORD val);
void CHardWare::INWORD(WORD adr,WORD *val);

2. Ввод/вывод команд и данных в память устройств спектрометра

DWORD CHardWare::writeword(UINT ndev, WORD val);
DWORD CHardWare::readword(UINT ndev, WORD *val);
DWORD CHardWare::resetaddr(UINT ndev);
DWORD CHardWare::incraddr(UINT ndev);

3. Ввод/вывод массивов в память устройств

int CHardWare::GetMemSize(UINT ndev);
int CHardWare::GetMask(UINT ndev);
int CHardWare::WriteBuf(UINT ndev,PWORD buf,int len);
int CHardWare::ReadBuf(UINT ndev,PWORD buf,int len);

Программная часть

Рисунок 4. Структура программы тестирования спектрометра

Режим 1. Запись данных на устройство, чтение данных с устройства, проверка (сравнение записанных и считанных данных).

Режим 2. Запись данных на устройство, чтение данных с устройства, проверка, повтор до обнаружения первой ошибки.

Режим 3. Запись или чтение на указанный адрес порта ввода/вывода однократно.

Режим 4. Циклическое повторение записи или чтения с интервалом, указанным пользователем.

Если организовать запуск функции тестирования в основном потоке, то во время её выполнения работа с интерфейсом программы, включая кнопку Стоп , будут недоступны, а так же не будет производиться прорисовка результатов выполнения. Режим стресс-тестирования (режим 2) может занять длительное время, а режим циклического тестирования (режим 4) вообще не сможет быть остановлен. Поэтому при нажатии кнопки Пуск в зависимости от указанных пользователем параметров тестирующая функция запускается в отдельном потоке.

void Cmain::OnStart()

{

DWORD ExitCode;

CString pusk; //состояние кнопки пуск

m_start.GetWindowText(pusk);

nTab = m_ctrTab.GetCurSel();

if (nTab==0){ //Если выбрана первая вкладка

…………………

if (pusk == "Пуск"){

…………………

//запускаем поток

PWinThread = AfxBeginThread(fContr,this);

}else{

//если поток не окончен

::GetExitCodeThread(PWinThread->m_hThread,&ExitCode);

if (ExitCode == STILL_ACTIVE){

TerminateThread(PWinThread->m_hThread,0);

delete PWinThread;//удаляем

…………………

}

};

} else { //если вторая вкладка

if (pusk == "Пуск"){

if(ppage2->m_bRepeatMode.GetCheck()==BST_CHECKED)

{ //если выбран циклический режим

…………………

//запускаем поток

PWinThread = AfxBeginThread(fCikl,this);

} else {//запускаем поток

PWinThread = AfxBeginThread(fAddr,this);

};

}else{

…………………

//если поток не окончен

::GetExitCodeThread(PWinThread->m_hThread,&ExitCode);

if (ExitCode == STILL_ACTIVE){

AfxEndThread (0); //останавливаем поток

TerminateThread(PWinThread->m_hThread,0);

delete PWinThread;//удаляем

}

};

}

}

Пользовательский интерфейс

При запуске появляется окно программы и вкладка Тест устройств . В блоке Тип тестирования возможность выбора типа тестирования, в блоке Тестируемые устройства выбор доступных для проверки устройств.

Рисунок 5. Закладка Тест устройств пользовательского интерфейса программы

На вкладке Тест ввода/вывода в блоке Тестирование возможность выбора тестируемого адреса, типа уровня тестирования. В блоке Параметры чтение данных с адреса или запись данных на адрес, а так же формат представления (система счисления) данных поля Содержание записи .

Рисунок 6. Закладка Тест ввода/вывода пользовательского интерфейса программы

Результаты работы программы

При нажатии кнопки Пуск начинается процесс тестирования.

Тест устройств. Внизу окна с вкладкой Тест устройств появляется область с таблицей, в которой выводятся ошибки устройств (Рисунок 7).

Рисунок 7. Окно с результатами тестирования устройств

Следующая таблица описывает основные типы аппаратных ошибок и неполадки, которыми они могли быть вызваны.

Таблица 1. Типы аппаратных ошибок

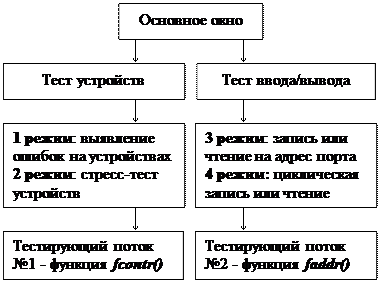
При несовпадении результатов тестирований разными уровнями доступа диагностируются ошибки драйвера.

Тест ввода/вывода . Используется для проверки интерфейсной логики устройств спектрометра с использованием осциллографа. Диагностируются, как правило, ошибки монтажа электронных компонентов.

Заключение

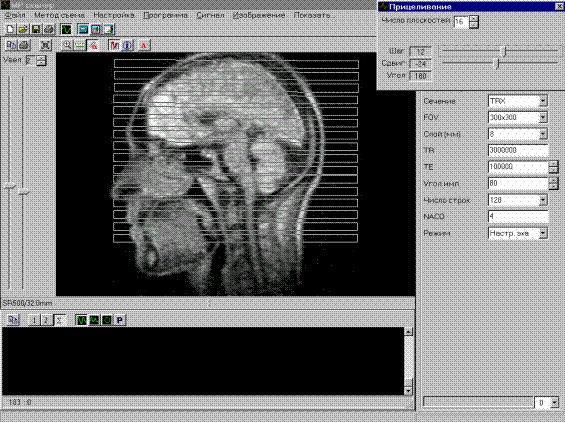
Графический интерфейс разработанной системы реализует удобный механизм диагностирования аппаратных неисправностей блоков радиоспектрометра, а так же отладки драйверов верхнего уровня программного комплекса mrscan. На данный момент программа введена в эксплуатацию и применяется разработчиками в лаборатории для выявления аппаратных неисправностей собранных или эксплуатируемых спектрометров.

В процессе выполнения данной работы свои знания и умения в области математики и программирования применила в прикладных науках – радиофизике и медицине. Приняла участие в серьезном и интересном научном проекте и процессе производства важного медицинского оборудования. Ознакомилась с работой и взаимодействием в команде ученых разных специальностей.

Моделирование строения атома

Попытка постигнуть основы мироздания с помощью физики - наиболее естественна. Совершается она уже многие тысячелетия. Сначала строение вещества пытались объяснить понятием материи, затем физики пришли к мысли о том, что в основе мира лежат неделимые атомы. Атомы, как оказалось, делятся. Физики стали эксплуатировать идею, что в основе мироздания находятся элементарные частицы. У современной физики возникло серьезное опасение, что и элементарные частицы имеют сложное строение и могут делиться. Основа мира, в этой связи, снова становится призраком, и снова нет достаточно четкого и ясного ответа.

Движение электрона в кулоновском поле ядра

Моделирование свойств микроэлементов - составная часть общей стратегии исследований, роль которой становится все более активной. Основные причины определяются успехами развития теоретических представлений о строении веществ и фантастическими достижениями компьютерных технологий.

Если придерживаться законов классической нерелятивистской квантовой физики, то движение электрона в кулоновском поле ядра описывает основное динамическое уравнение нерелятивистской квантовой механики - уравнение Шрёдингера. В разумности модели молекулы, используемой для квантово-химических построений, согласно которой анализу подлежит система ядер и электронов и ее поведение, описываемое уравнениями квантовой теории, сомнений нет. Вся совокупность экспериментальных данных, полученных разными методами, не противоречит этой модели.

Трудности получения значимых результатов на ее основе связаны с тем, что она слишком обща и всеобъемлюща, так что численное решение уравнений представляет крайне сложную задачу. Приходится делать немалое число шагов на пути создания практичных алгоритмов расчетов свойств молекул, межмолекулярных комплексов и твердых тел.

Мною была проделана научно-исследовательская работа, разработан и реализован алгоритм решения уравнения Шрёдингера для задачи движения электрона в кулоновском поле ядра.

Постановка задачи

Гамильтониан (оператор набла) - квантовомеханический оператор, соответствующий функции Гамильтона в классической механике и определяющий эволюцию квантовой системы. В представлении Шрёдингера эта эволюция описывается зависимостью от времени вектора состояния |Ψ > системы, который удовлетворяет уравнению Шрёдингера.

(1)

где Н - гамильтониан. Если классическая функция Гамильтона не зависит явно от времени, то она является интегралом движения и значение её совпадает с энергией системы. Соответственно гамильтониан системы в этом случае является оператором энергии. Оператор Гамильтона в случае движения электрона в поле ядра будет состоять из операторов кинетической энергии электрона и взаимодействия электрона с ядром.

(2)

При решении этого уравнения будем использовались следующие математические операции: переход в сферические координаты; решение дифференциального уравнения второго порядка в частных производных методом разделения переменных; разложение функции в ряд по степеням z; полиномы Лежандра; оператор Лапласа и Гамильтона; многочлены Чебышева-Лагерра; сферические функции (гармоники); условие нормировки решения уравнения Шрёдингера.

где Ω область определения Ψ(x,y,z).

Ψ(x,y,z) волновая функция прямого физического смысла не имеет. Смысл имеет квадрат модуля волновой функции |Ψ|2 как плотность вероятности обнаружения частицы в точке пространства (x,y,z) области определения Ψ(x,y,z).

Вывод алгоритма

В работе был создан алгоритм для вычисления этой плотности. Искалось решение в виде: и выведены следующие формулы:

Для решения уравнения Θ(θ) необходимо разбираться в следующих понятиях.

Орбиталь – это некоторый объем пространства, где вероятность нахождения электрона составляет не менее 90%.

Квантовые числа - энергетические параметры, определяющие состояние электрона и тип атомной орбитали, на которой он находится.

1. Главное квантовое число n определяет общую энергию электрона и степень его удаления от ядра (номер энергетического уровня); оно принимает любые целочисленные значения, начиная с 1 (n=1,2,3,...).

2. Орбитальное (побочное или азимутальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n-1 (l = 0,1, 2, 3, ..., n-1 ). Каждому значению l соответствует орбиталь особой формы: l=0 – s-орбитали; l=1 – р-орбитали (3 типа, отличающихся магнитным квантовым числом m ); l=2 – d-орбитали (5 типов), l=3 – f-орбитали (7 типов).

3. Магнитное квантовое число m определяет ориентацию орбитали в пространстве относительно внешнего магнитного или электрического поля. Его значения изменяются от – l до + l , включая 0. Например, при l=1 число m принимает 3 значения: +1, 0, -1 , поэтому сущ. 3 типа: p _x ,p _y ,p _z .

4. Спиновое квантовое число s может принимать лишь два возможных значения ±½. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона, называемого спином. Для обозначения электронов с различными спинами используются символы: ↑ и ↓.

Произведение найденных функций Θ(θ) и Ф(ф) представляет собой угловую часть волновой функции и называется сферической гармоникой Y _lm (θ,φ)

Решение радиального уравнения было следующим:

Полученные результаты

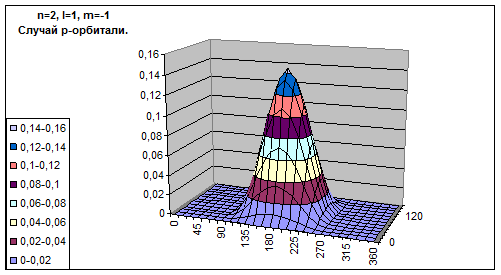
На основе выведенной формулы была составлена программа для подсчета вероятности нахождения электрона в точке пространства при конкретных квантовых числах. Графики вероятностей обнаружения частицы в данных углах при максимально вероятном при этих углах радиусе выглядят так.

Литературный обзор

Основоположником отечественного математического моделирования является академик А. А. Самарский, сформулировавший методологию, в кратком виде выраженную знаменитой триадой "модель - алгоритм - программа". Эта методология получила свое развитие в виде технологии "вычислительного эксперимента". В нашей стране имеют давние традиции исследования по механике жидкости и газа на основе уравнений Навье Стокса. Начало им положено ещё в первой половине 60-х годов в трудах участников семинара НИИ ВЦ МГУ по численным методам аэромеханики, работавшего под руководством Г.И. Петрова, Л.А. Чудова, Г.Ф. Теленина, Г.С. Рослякова. Эти работы удачно развивались благодаря успешным достижениям советских учёных в вычислительной математике. Среди многих рассматривавшихся в то время классов задач гидро- и аэродинамики, решение которых не могло быть получено в рамках теории пограничного слоя или невязкого газа (отрывные течения, взаимодействие ударной волны и пограничного слоя, структура ударной волны и т.д.), в работах В.И. Полежаева было значительно продвинуто изучение естественно-конвективных процессов. Эффективные численные методы и программы, разработанные для этого класса задач, позволили уже на ЭВМ второго поколения решить многие практически важные задачи: изучение эффективности тепловой изоляции, теплообмен и температурное расслоение при хранении жидкости в сосудах, конвекция в глубокой атмосфере для интерпретации данных зондирования атмосферы Венеры, исследование гидромеханики невесомости и анализ результатов технологических экспериментов в космосе..

На данный момент имеется немало литературы, излагающей теоретические основы математического моделирования и методов поиска решения. А так же литературы по каждому конкретному направлению научных исследований, в которой описываются модели и методы, эффективные в особенностях прикладной области. Одними из самых популярных областей применения математических методов являются: экономико-математическое моделирование (автоматизированные системы управления, прогнозирование изменений на рынке); математическое моделирование биологических процессов (биофизика, медицина); моделирование промышленных систем; модели нефтедобычи (пластовые структуры, залежи месторождений).

Не смотря на обширный объем литературы по данной тематике, многие области до сих пор остаются малоизученными математиками, хотя и остро нуждаются в применении математического аппарата (например, медицина). Помимо того, типология процесса не может учесть весь класс задач прикладной области, а в каждом частном случае существенное влияние могут оказывать любые особенности решаемой задачи.

Следующие источники использовались мной:

1. «Математическое моделирование. Идеи. Методы. Примеры». Монография А. А. Самарский, А. П. Михайлов. Издательство: М.:ФИЗМАТЛИТ, 2005г.
-- В монографии представлены методы и примеры построения и анализа математических моделей для различных задач механики, физики, биологии, экономики, социологии на основе использования фундаментальных законов природы, вариационных принципов, метода аналогий.

2. «Математическое моделирование технических систем». Учебник для вузов. В.П.Тарасик. Издательство: Минск: Дизайн ПРО, 2004 г.
-- Изложены основы методологии математического моделирования и проведения вычислительных экспериментов на ЭВМ и процессе проектирования сложных технических систем. Рассмотрены принципы и современные методы построения детерминированных и вероятностных, теоретических и экспериментальных факторных моделей, численные методы решения систем алгебраических и дифференциальных уравнений и задач многокритериальной оптимизации.

3. «Математическое моделирование пластовых систем». Пер. с англ. Х. Азиз, Э. Сеттари. Серия: Современные нефтегазовые технологии. Издательство: М., Ижевск: Институт компьютерных исследований, 2004г.
-- Изложены теоретические основы математического моделирования пластовых систем и описаны методы решения уравнений фильтрации с помощью вычислительных машин. Даны рекомендации по конструированию математических и компьютерных моделей, их анализ и примеры программных систем. Для инженерно-технических работников нефтяной промышленности, научно-исследовательских организаций и высших учебных заведений, занимающихся анализом и проектированием разработки нефтяных месторождений, а также для студентов вузов. Репринтное издание (оригинальное издание: М.: "Недра", 1982 г.).

4. «Математическое моделирование в биофизике. Введение в теоретическую биофизику» Ю. М. Романовский. Издательство: М.; Ижевск: Институт компьютерных исследований , 2004г.
-- В книге изложены основные принципы построения математических моделей биологических процессов и методы их исследования. Рассмотрены как точечные модели, описывающие поведение пространственно однородных процессов, так и модели, описывающие образование пространственных структур, распространение волн в активной среде и синхронизацию нелинейных осцилляторов. Обсуждаются следующие вопросы: возникновение жизни и эволюция видов; дифференциация ткани и морфогенез; культивирование микроорганизмов и инженерная микробиология; динамика иммунной реакции; термодинамика открытых систем и ее роль в описании биологических процессов.

5. «Математическое и компьютерное моделирование». Вводный курс: Учеб. пособие :Ю. Ю. Тарасевич.
-- В первой части автор на примерах из физики, химии, экологии показывает, как составляют и анализируют дифференциальные модели. Вторая часть посвящена задачам, когда качественный анализ затруднен или невозможен и требует прямое компьютерное моделирование процесса. Изложенное подкрепляется значительным количеством иллюстративного материала и в большинстве случаев достаточно подробными математическими выкладками. В то же время ряд примеров несомненно предполагает и большую самостоятельную работу студентов по составлению компьютерных программ и анализу полученных результатов.

6. «Введение в анализ, синтез и моделирование систем» Учеб. пособие В. М. Казиев. Серия: Основы информационных технологий. Издательство: М.: Интернет-Университет Информационных Технологий: БИНОМ. Лаборатория знаний, 2006г.
-- В курсе изложены основы системного анализа, синтеза и моделирования систем, которые необходимы при исследовании междисциплинарных проблем, их системно-синергетических основ и связей. Курс предназначен для студентов, интересующихся не только тем, как получить конкретное решение конкретной проблемы (что достаточно важно), но и тем, как ставить, описывать, исследовать и использовать такие задачи, находить и изучать общее в развивающихся системах различной природы, особенно, в информационных системах.

7. «Информационные технологии в медико-биологических исследованиях» Вячеслав Дюк, Владимир Эмануэль. - М. [и др.]: Питер, 2003 (ГП Техн. кн.). - 528 с. : ил.; 24 см.
-- В книге дается целостное представление о современных информационных технологиях в медико-биологических исследованиях и приводятся сведения о наиболее передовых теоретических и практических решениях в этой области.

8. Диссертац. «Дискретно-логические методы принятия решений в информационных медицинских диагностических системах» Шустерман И.Л., к.т.н.. 05.13.01. Уфа 2004, 149 с. ил.
-- Здравоохранение. Медицинские науки -- Методы и техника -- Математические методы -- Кибернетика в медицине.
Системный анализ, управление и обработка информации (по отраслям)

9. «Гибкие элементы медицинских систем» П.И. Бегун. - СПб. : Политехника, 2002. - 295 с. : ил., табл.; 22 см.
-- Книга содержит: современное состояние биомеханических исследований гибких элементов медицинских систем; моделирование и исследование гибких элементов структур человеческого организма в норме, патологии и при хирургических операциях.

10. «Математические модели в биологии, экологии и медицине». Герасимов, А. Н. Учеб. пособие / М-во общ. и проф. образования РФ. Фак. эксперим. и теорет. физики. - М. : Моск. гос. инж.- физ. ин-т (техн. ун-т), 1998. - 40 с. : ил; 20 см.
-- Общая экология -- Методика и техника научно-исследовательской работы -- Математические методы -- Учебник для высшей школы. Математическое моделирование в биологии.

11. «Физиологическая и медицинская информатика : Сб. науч. тр. / АН УССР, Ин-т кибернетики им. В. М. Глушкова, Науч. совет по пробл. "Кибернетика"; [Редкол.: Н. М. Амосов (отв. ред.) и др.]. - Киев : ИК, 1990. 76 с.: ил; 21. Физиологические функции, Математическое моделирование