Алгебра и топология
Определения.
1. Общая алгебра
– часто алгебра, занимающаяся изучением тех или иных алгебраических систем, включающая в себя теории групп, колец, модулей (абелева группа с кольцом операторов), подгрупп, решеток (структур) и т. п. .
Если универсальная алгебра (см. §2.1, п.1) снабжена порядком или топологией, согласованным с операциями, то возникает частично упорядоченная или топологическая алгебра соответственно. Исследование этих объектов также относится к общей алгебре.
Наиболее развиты в общей алгебре теории частично упорядоченных и топологических групп и колец. Другими направлениями являются исследования структур, универсальных алгебр и категорий. Вскрытие связей алгебр и математической логики привело к появлению теории моделей и алгебраических систем, кратко раскрывавшихся ранее (см. §3.1, п. 3.3). Результаты этих исследований находят приложения в ряде областей, например, в алгебраической теории автоматов, алгебре алгоритмов и алгебраической теории информации (главным образом в том направлении, которое связано с теорией кодирования и декодирования).
Немаловажно и другое замечание общей алгебры – ее связь с топологией.
Предметом исследований объектов являются: установление их соответствия, образование изотопий, наличие и сохранение характерных свойств, введение классов, категорий и т. п. .
Результаты обобщений позволяют надежно обосновывать рациональные пути конструктивных практических методов, подобных уже упоминавшихся ранее (§2.2, п. 2.4, §2.3, п. 6-11).
В §§2.2 и 2.3 приведены многие определения из входящих в круг понятий общей алгебры. Однако следует остановиться еще на ряде терминов.
Универсальная алгебра
– это алгебраическая система с пустым множеством отношений (часто называют просто алгебра). Если к основным операциям алгебры А
присоединяются все производные операции (например, как в §2.3, п. 6), то возникает универсальная алгебра Â
большей сигнатуры. Равенство Â
=  возможное и при А
¹В
, приводит к понятию рациональной дививалентности
универсальных алгебр.
возможное и при А
¹В
, приводит к понятию рациональной дививалентности
универсальных алгебр.
Универсальная алгебра называется функционально полной
, если всякая операция на ее носителе принадлежит клону*
, порожденному ее основными операциями и константами. Если исключаются константы, то универсальная алгебра называется строго функционально
полной. Всякая функционально полная универсальная алгебра конечна.
В общей алгебре дается характеристика многообразия универсальных алгебр.
Частично упорядоченная группа
– группа Gj
, на которой задано отношение частичного порядка £ такое, что для любых a, b, x, y из G неравенство a£b влечет за собой xay£xby.
Множество 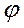 ={xÎG½x³1} частично упорядоченной группы, называемое положительным конусом
или целой частью
, группы G, обладает следующими свойствами: ={xÎG½x³1} частично упорядоченной группы, называемое положительным конусом
или целой частью
, группы G, обладает следующими свойствами:
1) 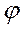 × P Í P; 2) × P Í P; 2) 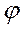 Ç P-1
={1}; 3) x-1
PxÍ Ç P-1
={1}; 3) x-1
PxÍ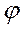 , ,
для любых xÎG.
Пример5.1
. Частично упорядоченными группами являются:
1. Аддитивная группа действительных чисел с обычным порядком;
2. Группа F(C, R) функций, заданных на произвольном множестве C со значениями R, с операцией:
(f+g)(x)=f(x)+g(x)
и отношением порядка f£g, если f(x) £g(x) для всех xÎC.
Важный класс частично упорядоченных групп – структурно(решеточно)упорядоченная группа
, l
-группа
, – группа G
с сигнатурой: <×, -1
,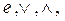 >, удовлетворяющая аксиомам: >, удовлетворяющая аксиомам:
1)
 <G, ×, -1
, <G, ×, -1
,  , > – группа; , > – группа;2) <G, 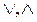 , > – решетка; , > – решетка;
3) x(y z)t=xyt z)t=xyt xzt, xzt,
x(y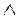 z)t=xyt z)t=xyt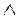 xzt, xzt,
для любых x, y, z, tÎG.
Решетка структурно упорядоченной группы дистрибутивна.
Модулем
элемента x называют элемент |x|=x x-1
. x-1
.
Положительной частью элемента x является x+
=x  и отрицательной x-
=x и отрицательной x-
=x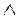  . .
Другой важный класс – линейно упорядоченная группа
G
, являющаяся группой относительно операции умножения, линейно упорядоченным множеством относительно бинарного отношения порядка £ и удовлетворяющая аксиоме: для любых элементов x, y, zÎG
из x£y следует xz£yz и zx£zy.
Частично упорядоченное кольцо
K
является частично упорядоченной группой по сложению, в котором для любых a, b, cÎK
неравенства a£b и c³0 влекут за собой неравенства ac£bc и ca£cb.
Пример 5.2. Упорядоченными кольцами являются:
1. Упорядоченное поле
– линейно упорядоченное кольцо, являющееся полем (поле действительных чисел с обычным порядком);
2. Кольцо действительных функций на множестве C, где f£g означает, что f(x)£g(x) для всех xÎC;
3. Кольцо матриц над упорядоченным кольцом K
, где по определению  ,если aij
£bij
для всех i, j. ,если aij
£bij
для всех i, j.
Если K
– упорядоченное кольцо, то множество 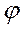 ={x|xÎK
, x³0} называется его положительным конусом, однозначно определяющим порядок кольца K
(x£y, тогда и только тогда, когда (y-x)ÎK
). Подмножество ={x|xÎK
, x³0} называется его положительным конусом, однозначно определяющим порядок кольца K
(x£y, тогда и только тогда, когда (y-x)ÎK
). Подмножество 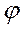 ÍK
служит положительным конусом для некоторого порядка, в том и только в том случае, когда ÍK
служит положительным конусом для некоторого порядка, в том и только в том случае, когда 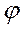 Ç(-P)={0}, P+PÍ Ç(-P)={0}, P+PÍ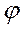 и и 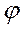 ×PÍ ×PÍ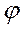 . .
Равенство 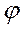 È(-P)=K
равносильно линейности этого порядка. È(-P)=K
равносильно линейности этого порядка.
2. Топология
– раздел математики, назначением которого является выяснение и исследование идеи непрерывности в широком понимании, включая и дискретность, как фактор снятия непрерывности. Топология в настоящее время достигла высокого уровня развития. Представляется, что методы и идеи топологии должны найти, в возможном специфическом предложении, свое место и при исследованиях дискретных структур (здесь, по-видимому, на первое место может претендовать теория графов).
Главной задачей
топологии является выделение и изучение топологических свойств пространств или топологических инвариантов
: связность, компактность, размерность, вес, фундаментальная группа, группа гомологий и другие.
Центральным объектом
исследования в топологии считается тройка (C,f,U), где f – непрерывное отображение топологического пространства C в топологическое пространство U.
Отсюда важнейшими понятиями топологии являются понятия: гомоморфизма (см. §2.3, п. 12) и топологическое пространство.
Пространство
, в общем случае, это понятие, сложившееся в результате обобщения и видоизменения понятий геометрии евклидова пространства (пространство Лобачевского, многомерная геометрия и т. п.).
Топологическое пространство
– совокупность двух объектов: множества C, состоящего из элементов произвольной природы, называемыми точками данного пространства, и из введенной в это множество топологической структуры (топологии)
. Топология
– это та или иная совокупность подмножеств U
(открытых или замкнутых) множества C, удовлетворяющая трем условиям:
1) ÆÎU
, CÎU
;
2) пересечение двух множеств из U
принадлежит U
;
3) Объединение любой совокупности множеств из U
принадлежит U
.
Топологическое пространство обозначают (C,U
), что нередко сокращается до обозначения Т
или просто C.
Топология может быть задана и отношением замыкания
. Отношение замыкания имеет место тогда, когда всякому элементу xÎC сопоставлен однозначно определенный элемент 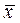 ÎC, называемый замыканием
элемента x. При этом для всех x, yÎC должны выполняться следующие требования: ÎC, называемый замыканием
элемента x. При этом для всех x, yÎC должны выполняться следующие требования:
1) x£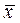 ; ;
2) если x£y, то 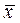 £ £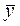 ; ;
3) 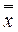 = =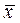 , то есть замыкание любого элемента совпадает со своим замыканием; , то есть замыкание любого элемента совпадает со своим замыканием;
4) замыкание объединения двух (а поэтому и любого конечного числа) подмножеств из C равно объединению замыканий этих подмножеств:  ; ;
5) всякое подмножество, состоящее из одного элемента, замкнуто.
Элемент x называется замкнутым
если он совпадает со своим замыканием.
Во всяком частично упорядоченном множестве можно давать тривиальное замыкание
, полагая  = =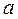 для всех для всех 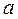 . .
Отношение замыкания задано также, если система подмножеств множества C частично упорядочена по теоретико-множественному включению.
Если в множестве C задано отношение замыкания, то само множество
Cзамкнуто
, как замыкание самого себя. И пересечение любой системы замкнутых подмножеств в
C само замкнуто
.
Системы открытых и замкнутых множеств являются взаимно
дополняющимися
.
Ряд понятий топологии (окрестность точки, точки прикосновения и другие) рассматриваются, как правило, в основном курсе высшей математики. Здесь остановимся лишь на тех положениях, которые обычно не находят там отражения.
Связность
– свойство топологического пространства, состоящее в том, что пространство нельзя представить в виде суммы двух отдельных друг от друга частей – непустых непересекающихся открыто-замкнутых подмножеств. Пространство, не являющееся связным, называется несвязным
. Например, обычная евклидова плоскость – связное пространство; если удалить какую-либо окружность, не сводящуюся к точке, то остаток уже несвязен. Связность пространства сохраняется при гомеоморфизмах.
Абстрактное свойство связности является обобщением линейной связности, то есть свойства пространства, заключающегося в возможности связать любые его две точки некоторым путем.
Компактность
– свойство, состоящее в том, что каждое бесконечное подмножество пространства имеет предельную точку
, то есть такую точку данного подмножества, любая окрестность которой содержит, по крайней мере, одну точку этого подмножества, отличную от точки именуемой предельной. Множество, содержащее все свои предельные точки, называется замкнутым
, а совокупность всех предельных точек называется производным множеством
.
Размерность
– целочисленный инвариант пространства C (обозначение dimC – Лебега размерность
), определяемый следующим образом:
– dimC = -1, если C=Æ;
– dimC£n, если топологическое пространство не пустое и не более, чем n – мерно;
– dimC = n – пространство называется n-мерным.
Вес
– кардинальное наименьшее число, являющееся мощностью базы
топологического пространства, то есть такого семейства B открытых подмножеств пространства C, что каждое открытое множество GÌC является объединением элементов 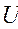 ÌB. ÌB.
Фундаментальная группа
(группа Пуанкаре) – группа 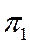 (C, x0
) пунктированного, то есть с отмеченного точкой x0
, пространства C. Элементами фундаментальной группы служат гомотопические классы замкнутых путей в C ( (C, x0
) пунктированного, то есть с отмеченного точкой x0
, пространства C. Элементами фундаментальной группы служат гомотопические классы замкнутых путей в C (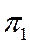 – символ фундаментальной группы). – символ фундаментальной группы).
Гомотопия
, гомотопность двух непрерывных отображений f и g (f, g: C®U) есть существование такого семейства непрерывных отображений ft
: C®U, непрерывно зависящих от параметра tÎ[0,1], что f0
=fn
, f1
=g. Это семейство (называемое гомотопией, связывающей f с g) является путем в пространстве F(C,U) всех непрерывных отображений C®U, связывающих точку f с точкой g.
Гомологии группа
топологического пространства – группа, которая ставится в соответствие топологическому пространству с целью алгебраического исследования его топологических свойств в рамках алгебраической топологии
. Частью алгебраической топологии является теория гомологии
, осуществляющая связь между топологическими и алгебраическими понятиями: приводя в соответствие каждому пространству определенную последовательность групп, а непрерывному отображению пространства – гомоморфизмы соответствующих групп.
Таким образом, по свойствам групп и их гомоморфизмов можно судить о свойствах пространства и отображений, в частности о тех, что приводились выше.
3. Метрика
– понятие, характеризующее «расстояние» на множестве C. Это некоторая функция  с неотрицательными действительными значениями, определяемая на декартовом произведении C´C. Функция с неотрицательными действительными значениями, определяемая на декартовом произведении C´C. Функция  должна удовлетворять при любых x, yÎC условиям: должна удовлетворять при любых x, yÎC условиям:
1)  (x, y)=0 тогда и только тогда, когда x=y (аксиома тождества); (x, y)=0 тогда и только тогда, когда x=y (аксиома тождества);
2)  (x, y) + (x, y) +  (y, z) ³ (y, z) ³ (x, z) (аксиома треугольника); (x, z) (аксиома треугольника);
3)  (x, y) = (x, y) = (y, x) (аксиома симметрии). (y, x) (аксиома симметрии).
Пример 5.3.
1. На любом множестве имеется дискретная (тривиальная)
метрика:  =1, (x¹y) и =1, (x¹y) и  =0, (x=y). =0, (x=y).
2. В пространстве действительных чисел Rn
возможны метрики:
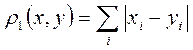
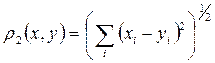 , ,
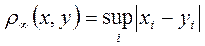 . .
Или в общем виде:
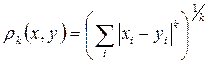 , ,
здесь {xi
}, {yi
}ÎRn
.
3. В функциональных пространствах (см. ниже), в частности, для множества непрерывных функций на отрезке [a,b] существуют:
· равномерная метрика:
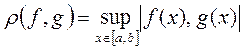 , ,
· интегральная метрика:
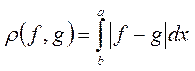 . .
4. Для метрического пространства возможна внутренняя метрика:
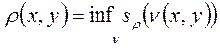
при условии, что любые две точки пространства с метрикой , соединимы кривой n(x,y), а , соединимы кривой n(x,y), а 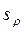 – длина кривой в метрике – длина кривой в метрике  . .
5. Метрика для нормированных множеств (определена действительная функция и (мера)) булевой алгебры представляется выражением:  . .
Обычно m(1)=1, а m(0)=0.
5.2 Пространства.
1. Метризуеимое и метрическое пространства.
Множество C, на котором может быть введена метрика, называется метризуемым пространством.
Множество C, наделенное метрикой – метрическое пространство
.
Один из общих критериев метризуемости, основанный на концепции локальной конечности, формируется так: пространство C метризуемо в том и только в том случае, если оно регулярно и обладает базой, распадающейся на счетное множество локально конечных семейств множеств.
Регулярным пространством
называется топологическое пространство, в котором для каждой точки x и каждого не содержащего ее замкнутого множества A найдутся непересекающиеся множества B и C такие, что xÎB и AÎC.
Локально конечное семейств
F множеств – такое семейство, что у каждой точки пространства C есть окрестность, пересекающаяся лишь с конечным множеством его элементов.
Класс метрических пространств внутренним образом связан с классом метризуемых пространств. В этой связи следует отметить, что метрика индуцирует (порождает) топологию 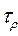 и две метрики эквивалентны, если они индуцируют одну и ту же топологию. и две метрики эквивалентны, если они индуцируют одну и ту же топологию.
Расстояние между точками можно использовать для определения расстояния между точкой и множеством.
Расстояние
 (x, A) от точки
xдо множества
А в метрическом пространстве {C, (x, A) от точки
xдо множества
А в метрическом пространстве {C,  } определяется как inf{ } определяется как inf{ (x, y) |yÎA}. Точка x объявляется абсолютно близкой ко множеству A, если (x, y) |yÎA}. Точка x объявляется абсолютно близкой ко множеству A, если  (x, A)=0. (x, A)=0.
Замыканием
[A] множества А в {C,  } называется множество всех точек из C, абсолютно близких к А. Однозначно отвечающая этой операции топология } называется множество всех точек из C, абсолютно близких к А. Однозначно отвечающая этой операции топология 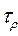 на множестве C и называется топологией, порожденной
на Cметрикой на множестве C и называется топологией, порожденной
на Cметрикой
 . .
Различные варианты метрик приведены в примере 5.3.
Важным подклассом метрических пространств, связанным с теорией алгоритмов, являются эффективно метрические пространства
. Это метрические пространства, рассматриваемые вместе с некоторой своей нумерацией, причем требуется, чтобы расстояние между любыми двумя точками этого пространства были вычисленными дистрибутивными числами
и существовал алгоритм
, дающий программу вычисления такого числа по номерам точек (отсюда и термин вычислимые числа).
Числовой нумерацией
множества А называется произвольное отображение f произвольного множества QÌN; если при этом f(q)=a, то q называется f-номером
, или просто номером
, элемента а (aÎA и qÎQ).
Множество Q-основание
или номерное множество
нумерации f. Если Q=N, нумерация является натуральной
(простой
).
Нумерация называется разрешимой
, если существует алгоритм, который применим к любой паре элементов из Q и дает ответ на вопрос, являются ли они или нет номерами одного и того же элемента из А.
Если каждый элемент А имеет только один номер (то есть f – взаимно однозначное соответствие), нумерация называется однозначной
(без повторений
) нумерацией
.
Пример 5.4.
Рассмотрим множество V'u слов русского языка на основе русского алфавита А={Æ, а, б, в, …, ю, я} (|A|=32 буквы, включая пробел, обозначенный знаком Æ).
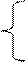 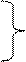 Один из примитивных методов кодирования слов uÎV является нумерация множества А букв алфавита числами натурального ряда N. Нетрудно увидеть, что в этом случае QÌN, если Q есть множество из каких-то тридцати двух чисел. Например, отображение на рисунке 5.1. Один из примитивных методов кодирования слов uÎV является нумерация множества А букв алфавита числами натурального ряда N. Нетрудно увидеть, что в этом случае QÌN, если Q есть множество из каких-то тридцати двух чисел. Например, отображение на рисунке 5.1.
4.1. Рис. 5.1.
Если будут нумероваться не только буквы алфавита, но и все образованные слова в каком-то порядке, считая в этом случае и буквы как однобуквенные слова, то Q=N. Номер очередного слова может определяться в соответствии с лексикографическим порядком (см. §1.2, п. 2). Очевидно, что в этом случае будем иметь соответствие g(q)=u, где u некоторое слово из множества слов V, и однозначную нумерацию.
Такого рода процедуру называют иногда арифметизацией
. Введенные какие-либо достаточно простые отображения f или g позволяют перевести отношения и операции, определенные на словах, в отношения и операции на номерах. Требование «достаточной простоты» отображения сводятся к тому, чтобы некоторые основные отношения (такие, как отношение вхождения
одного слова в другое, – например, вхождение слова «уда», – приспособление для ужения, – в слово на|уда|чу, и т. п.) и операции (такие, как операции соединения слов и т. п.) переходили в отношения и операции, имеющие простую алгоритмическую природу (см. дополнительно §3.3).
2. Линейные (векторные) и нормированные (банаховы) пространства
в контексте теории дискретных структур представляют наибольший интерес.
Векторное (линейное) пространство
над полем F – аддитивно записанная абелева группа V, в которой определено умножение на скаляр, то есть отображение F´V®V:(l,x)®lx, удовлетворяющее следующим аксиомам (x, yÎV; l, m, 1ÎF):
1) 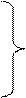 l(x+y) = lx+ly, l(x+y) = lx+ly,
2)
(l+m)x = lx+mx,3) (lm)x = l(mx),
4) 1×x = x
Элементы векторного пространства называются точками этого пространства либо векторами, а элементы поля F – скалярами.
Векторное пространство V есть частный случай модуля
над кольцом, а именно, V есть унитарный модуль
(модуль с единицей) над полем. Унитарный модуль над некоммутативным телом также называют векторным пространством над телом
.
Аксиомы (4.48) отражают аддитивность
и однородность
линейного пространства.
Пример5.5.
К числу линейных пространств относятся:
1. Множество вещественных чисел R
с обычно определенными операциями сложения и умножения.
2. Множество всех упорядоченных n-к вещественных чисел, если операции сложения и умножения на число определены следующим образом.
Если x=(x1
, …, xn
), y=( y1
, …, yn
), то x+y=(x1
+y1
, …, xn
+yn
);
 при x, yÎR
. при x, yÎR
.
3. Пространство функций  .Если для любых f(x), g(x)Î .Если для любых f(x), g(x)Î под f(x)+g(x) понимается сумма значений f и g, взятые при одних и тех же значениях x. То под lf(x) нужно понимать новую функцию, полученную из f(x) умножением всех ее значений на l. Нулевой функцией будет f(x)=0 на всем отрезке [a,b]. под f(x)+g(x) понимается сумма значений f и g, взятые при одних и тех же значениях x. То под lf(x) нужно понимать новую функцию, полученную из f(x) умножением всех ее значений на l. Нулевой функцией будет f(x)=0 на всем отрезке [a,b].
Линейное пространство получает законченное описание тогда, когда свойства аддитивности и однородности дополнены возможностью измерения величин самих элементов (векторов). Введение к понятию линейного нормированного пространства (банахова пространства)
, если для каждого xÎX существует неотрицательное число 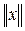 , называемое нормой
x. Норма , называемое нормой
x. Норма 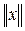 должна удовлетворять следующим условиям: должна удовлетворять следующим условиям:
1) 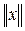 =0 тогда и только тогда, когда x=0; =0 тогда и только тогда, когда x=0;
2)  ; ;
3) 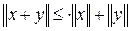 – неравенство треугольника. – неравенство треугольника.
В этом случае величина  обладает всеми свойствами меры обладает всеми свойствами меры  (x, y). Действительно: (x, y). Действительно:
1)  =0, если x-y=0, то есть x=y; =0, если x-y=0, то есть x=y;
2)  = =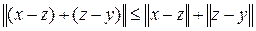 ; ;
3) учитывая, что y-x=-(x-y), находим 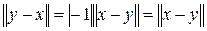 . .
Следовательно, линейное нормированное пространство является метрическим пространством с метрикой
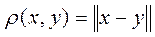 (5.3). (5.3).
Все рассмотренные ранее метрические пространства дополненные свойствами аддитивности и однородности, превращаются в нормированные линейные пространства. Для этих пространств обычно используют специальные обозначения.
Пример 5.6.
1. Пространство 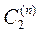 или или 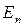 с нормой с нормой 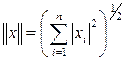 при n=1 при n=1 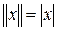 ; ;
2. Пространство 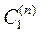 с нормой с нормой 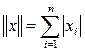 ; ;
3. Пространство  с нормой с нормой 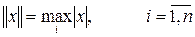 ; ;
4. Пространство 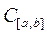 непрерывных функций f(t), определенных на промежутке [a,b], с нормой непрерывных функций f(t), определенных на промежутке [a,b], с нормой 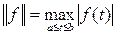 . .
3. Дискретные пространства и пространства близости
. Тривиальное замыкание, определенное ранее, удовлетворяет всем пяти условиям (см. §5.1, п. 2) и, следовательно, является топологией. Эта топология называется дискретной
. Все подмножества множества X будут в этой топологии и замкнутыми, и открытыми. Всякое множество может рассматриваться как дискретное топологическое пространство
, причем в конечных множествах, где всякое подмножество является объединением конечного числа элементов, возможна лишь дискретная топология.
Пример 5.7.
1. Если семейство U
совпадает с множеством B(X) всех подмножеств X (см. §1.1, п.3), то имеет место дискретная топология.
2. Дискретная топология индуцируется тривиальной метрикой (см. Пример 5.3
):
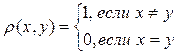 . .
В этом случае имеем дискретное топологическое пространство (X, 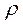 ). ).
Пример 5.8.
1. Если U
={Æ,X} – крайний случай совокупности U
, – то такое семейство определяет топологию на любом множестве X. Такая топология называется антидискретной
.
2. Простым примером не дискретного топологического пространства
служит прямая линия. Рассматривая ее как числовую прямую и определяя для каждого подмножества A, замыкание 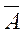 как совокупность чисел, являющихся пределами сходящихся последовательностей чисел из A, – получаем топологию, называемую естественно топологией
. Одной из полных систем окрестностей здесь служит система всех (открытых) интервалов. как совокупность чисел, являющихся пределами сходящихся последовательностей чисел из A, – получаем топологию, называемую естественно топологией
. Одной из полных систем окрестностей здесь служит система всех (открытых) интервалов.
Пространство близости
– множество X с бинарным отношением в на множестве всех его подмножеств, удовлетворяющее следующим аксиомам:
1) AdB равносильно BdA (симметричность);
2) Ad(BÈC) равносильно AdB или AdC (аддитивность);
3) AdA равносильно A¹Æ (рефлексивность).
Отношение в определяет близостную структуру, или просто близость
на X. При этом, если AdB, то A и B называются близкими
множествами, а если 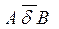 ( ( означает отрицание d), – то далекими
. означает отрицание d), – то далекими
.
Свойства близости пространства являются обобщением равномерных свойств метрического пространства аналогично тому, как в топологическом пространстве обобщаются его непрерывные свойства.
Понятие близостного пространства представляется полезным в решении проблем метризации путем равномерных покрытий множеств.
Покрытием
данного топологического пространства называется любая конечная совокупность его открытых множеств, дающих в своей сумме все это пространство. К числу важных покрытий, тесно связанных с покрытием Лебега размерности, относится e
-покрытие
отличительной особенностью которого является то, что все его элементы имеют диаметр <e.
Лебега размерность
и является той размерностью, которая определяется путем покрытий.
Взаимно однозначное отображение f множества X на множество Y называется близостным изоморфизмом относительно близостей
 на множествах X и Y. Соответственно, если f близостно непрерывно относительно на множествах X и Y. Соответственно, если f близостно непрерывно относительно  и обратное отображение f–1
близостно непрерывно относительно и обратное отображение f–1
близостно непрерывно относительно  . Близостный изоморфизм есть гомоморфизм индуцированных топологических пространств. . Близостный изоморфизм есть гомоморфизм индуцированных топологических пространств.
Два пространства близости (X, d) и (Y, 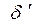 ) близостно изоморфны
, если существует близостный изоморфизм (X, d) и (Y, ) близостно изоморфны
, если существует близостный изоморфизм (X, d) и (Y,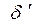 ). Изучение близостных инвариантов
является содержанием теории пространства близости. Каждый топологический инвариант является близостным инвариантом. ). Изучение близостных инвариантов
является содержанием теории пространства близости. Каждый топологический инвариант является близостным инвариантом.
Пример 5.9.
Каждая метрика  порождает близость в на множестве X. Два множества A, BÌX близки относительно в в том и только в том случае, если порождает близость в на множестве X. Два множества A, BÌX близки относительно в в том и только в том случае, если  (A, B)=0. Следовательно, если (A, B)=0. Следовательно, если  – произвольная метрика на множестве X и положим AdB тогда и только тогда, когда – произвольная метрика на множестве X и положим AdB тогда и только тогда, когда  (A, B)=0, то тем самым определяется близость в на множестве X. Близость в называется близостью индуцированной метрики (A, B)=0, то тем самым определяется близость в на множестве X. Близость в называется близостью индуцированной метрики
 . .
4. Метрика Хемминга
– имеет своим истоком проблемы кодирование теории информационных процессов. Основой данной метрики является метрика нормированных множеств булевой алгебры (см. п. 5, примера 5.3).
При формировании метрики Хемминга рассматривается векторное пространство над конечным полем характеристики 2–F2
, то есть двоичные векторы, как частично упорядоченный набор нулей и единиц (см., например §2.2, п. 8).
Метрикой (расстоянием)
Хемминга в между двумя векторами (словами, кодами и т. п.) является число мест, в которых символы двоичных векторов не совпадают.
Пример 5.10.
Пусть из всего множества возможных векторов, состоящих из n=8 символов 0 и 1, выбраны векторы-коды слов: ai
, aj
и ak
. Получим расстояние между ними в соответствие с приведенным определением:
| ai
= |
|| 0 1 1 0 1 0 1 1 || |
| aj
= |
|| 1 0 1 0 0 1 1 0 || |
| |ai
-aj
| |
* * * * * |
d(ai
-aj
)=5 |
| ak
= |
|| 0 1 1 0 1 0 1 0|| |
| |ai
-ak
| |
* |
d(ai
-ak
)=1 |
| |aj
-ak
| |
* * * * |
d(aj
-ak
)=4. |
Нетрудно проверить, что метрика Хемминга удовлетворяет всем аксиомам расстояния:
1) d(ai
,aj
)³0 и d(ai
,aj
)=0, тогда и только тогда, когда ai
=aj
;
2) d(ai
,aj
)+d(aj
,ak
)³d(ai
,ak
) (в приведенном примере 5+4>1; заметим также d(ai
,aj
)+d(ai
,ak
)³d(aj
,ak
) – (5+1>4) и d(ai
,ak
)+d(aj
,ak
)=d(ai
,aj
) – 1+4=5);
3) d(ai
,aj
)= d(aj
,ai
).
В отдельных случаях может представлять интерес так называемое приведенное расстояние Хемминга
– 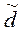 представляющее собой отношение расстояния dkn – размерности пространства. представляющее собой отношение расстояния dkn – размерности пространства.
Пример 5.10.а.
Для кодовых слов ai
, aj
и ak
из примера 5.10 относительное расстояние d1
будет 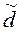 (ai
,aj
)= (ai
,aj
)=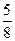 =0,625, =0,625, 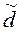 (ai
,ak
)=0,125 и (ai
,ak
)=0,125 и 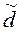 (aj
,ak
)=0,5. (aj
,ak
)=0,5.
5. Примеры метризации.
Метрика Хемминга может быть использована в различных задачах. Так в теории систем существует проблема оценки близости подпространства A, BÌX при оценке качеств систем одного и того же назначения. В исходной постановке эту проблему иллюстрирует пример 5.11.
Пример 5.11
. Пусть имеется несколько систем A1
,…,A,…,Am
( ), каждая из которых обладает своим набором полезных свойств из некоторого полезного набора качеств системы. Строго говоря, полезный набор, чаще всего, определить трудно. ), каждая из которых обладает своим набором полезных свойств из некоторого полезного набора качеств системы. Строго говоря, полезный набор, чаще всего, определить трудно.
Здесь возможны следующие варианты:
1. Состав свойств xj
(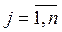 ) одинаков. Проблема выбора отсутствует. ) одинаков. Проблема выбора отсутствует.
2. Различное число свойств  при одинаковой их «значимости». Естественно, выбирается та система (×), которая имеет большее количество полезных свойств при одинаковой их «значимости». Естественно, выбирается та система (×), которая имеет большее количество полезных свойств 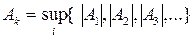 . .
При наличии нескольких одинаковых по количеству свойств систем – сокращается число систем, принимаемых во внимание.
3. Количество свойств в наборах одинаково, но их составы различны. Здесь может быть полезным использование метрики Хемминга. Так, применяя, например, таблицу «системы – свойства» (см. таблицу 5.1)решение можно получить на основе логической близости по расстоянию Хемминга между мажорантой функцией по составу свойств рассматриваемых систем и булевыми функциями свойств этих систем.
В таблице 5.1 учитываются лишь четыре системы A1
,A2
,A3
,A4
(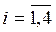 ). При этом каждая из систем обладает четырьмя из n=8 возможных свойств. ). При этом каждая из систем обладает четырьмя из n=8 возможных свойств.
Таблица 5.1.
Здесь «1» – наличие, «0» – отсутствие свойства.
Определение расстояния Хемминга векторами пространства свойств систем A1
,A2
,A3
и A4
и функцией 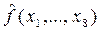 показывает, что лучшим приближением к набору наиболее «проявленных» свойств является система A3
. показывает, что лучшим приближением к набору наиболее «проявленных» свойств является система A3
.
В теории дискретных структур используется иногда понятие обобщенная метрика Хемминга
. Смысл обобщения состоит в распространении оценки расстояния и на нечеткие множества. Последнее означает (см §4.3, п.1) введение вместо дискретной функции принадлежности m(x)={0,1} («не принадлежит» рассматриваемому множеству –0, «принадлежит» – 1) функции принадлежности m(x), определенной на множестве рациональных чисел, обычно на отрезке m(x)=[0,1].
С формальной стороны такое «обобщение» переводит метрику Хемминга в общеизвестную форму линейной метрики (см. пример 5.3, п.2). В самом деле,
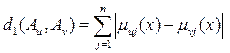 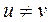 (5.4), (5.4),
подобна  (x, y) в п. 2 примера 5.3. (x, y) в п. 2 примера 5.3.
Представляется, что тонкость состоит в том, что фактически вводится в метрику некоторая функция-множитель – в данном случае характеристическая функция принадлежности
m(x) при этом часто неявно полагают все xij
={1} (как, кстати, и сделано в примере 5.11, в таблице 5.1 – свойства xj
(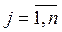 ) в общем существуют, но уровень их не определен и в данном случае, не учитывается). ) в общем существуют, но уровень их не определен и в данном случае, не учитывается).
Такой подход открывает широкий спектр «обобщений» путем введения разнообразных функций-множителей.
Так, например, в теории эффективности систем распространено применение весовой функции
, оценивающей «значимость» отдельный свойств (координат векторного пространства) в общем, показатель совершенства системы.
Отметим отличие весовой функции от характеристической. Значения весовой функции g(x), где xÎX, взаимосвязаны соотношением:
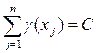 (5.5). (5.5).
Здесь C некоторая величина, зависящая от выбора множества значений функции g(x).
Так, значениями g(x) могут быть ранги элементов. В простейшем случае это натуральные числа номеров мест в соответствие со значимостью xj
ÎXj=1, 2,…, n=|X|. Тогда  . .
Чаще всего используют приведенные значения функции g(x)
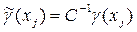 , ,
определенные на полуинтервале (0,1].
Функция принадлежности m(xj
) для каждого элемента xj
ÎX ограничена лишь тем множеством М, на котором она определена.
Обычно М задают на отрезке [0,1]. Если суммировать принадлежности элементов x из множества мощности |C|=n, то сумма будет лежать в пределах
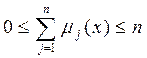 (5.6). (5.6).
При этом верхнее значение имеет место, когда все mj
=1, а нижнее при всех mj
=0, (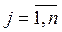 ). ).
Кроме того, алгебры весовых и характеристических функций различны. Первых – алгебра множеств рациональных чисел, а алгебра характеристических функций – одна из модификаций булевой алгебры (см. §2.3).
Если задать некоторую функцию f, например, предельную 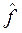 или среднюю или среднюю 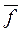 , в пространстве X, со значениями соответственно , в пространстве X, со значениями соответственно  или или 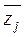 , то близость систем по своим свойствам к функции , то близость систем по своим свойствам к функции 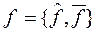 будут отражать метрики: будут отражать метрики:
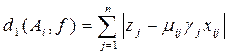 (5.7) (5.7)
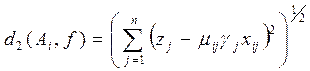 (5.8). (5.8).
Нетрудно видеть, что здесь весовая функция взята в виде набора постоянных коэффициентов, «взвешивающих» те или иные свойства системы в независимости от уровня этих свойств. При таких условиях на различие метрик d1
основное влияние оказывают значения m(x) и x. Однако при метриках d2
на их различие влияют все составляющие m(x), x и g.
В следующем примере 5.11.а дана детальная иллюстрация оценки близости в рассматриваемом пространстве X соответствующих множеств (систем) по набору их свойств на основе введения различных по структуре метрик.
Пример 5.11.а
. Используя в качестве исходных данных пример 5.11, получим сравнительные оценки близости множеств A1
,A2
,A3
и A4
.
С этой целью зададимся значениями показателя принадлежности m для всех возможных характеристик систем (табл. 5.2). При этом, там, где в табл. 5.1 показатель принадлежности равен 1, в табл. 5.2 назначим m(x)>0,5, в противоположном случае примем m(x)£0,5. В нижней строке табл. 5.2 приведены показатели для формирования мажорирующих функций. Здесь значения m(x) определялось по схеме.
||mij
|| Таблица 5.2
 xj xj
Ai
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
| A1
|
0,6 |
0,8 |
0,7 |
0,6 |
0,5 |
0,3 |
0,2 |
0,1 |
| A2
|
0,1 |
0,2 |
1,0 |
0,9 |
0,9 |
0,3 |
0,7 |
0,4 |
| A3
|
0,6 |
0,4 |
0,7 |
0,2 |
0,5 |
0,8 |
0,9 |
0,4 |
| A4
|
0,6 |
0,4 |
0,3 |
0,2 |
0,4 |
0,8 |
0,9 |
1,0 |
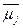 |
0,475 |
0,450 |
0,675 |
0,475 |
0,575 |
0,550 |
0,675 |
0,475 |
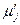 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
||xij
|| Таблица 5.3
 xj xj
Ai
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
| A1
|
0,9 |
0,8 |
0,6 |
0,6 |
0,2 |
0,1 |
0,1 |
0,2 |
| A2
|
0,2 |
0,1 |
0,6 |
0,7 |
0,8 |
0,1 |
0,9 |
0,1 |
| A3
|
0,2 |
0,2 |
0,3 |
0,1 |
0,1 |
0,9 |
0,8 |
0,6 |
| A4
|
0,6 |
0,2 |
0,1 |
0,1 |
0,2 |
0,6 |
0,6 |
0,2 |
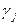 |
0,20 |
0,08 |
0,15 |
0,10 |
0,05 |
0,25 |
0,12 |
0,05 |
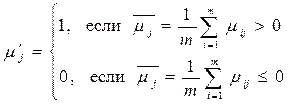 . .
Такой подход связан с тем, что ближайшими числами к 1, являются числа большие 0,5, а к 0 – меньшие 0,5.
Число 0,5 приравнивается к 0 из тех соображений, что булева мажоранта (см. пример 5.11) ровна нулю, если одинаково число единиц и нулей в множестве ее переменных.
Таблица 5.4, в которой в метрику введены только весовые коэффициенты, а показатели принадлежности точно такие же, какие использованы в таблице 5.1, показывает существование влияния весовых коэффициентов на близость к соответствующим функциям сравнения. При этом следует отметить совпадение оценки в предыдущем разделе примера по мажоранте и средней функции в данной части (вновь наибольшей близостью отличается система A3
).
Таблица 5.4
 Свойства Свойства
Системы
|
x1
|
x2
|
x3
|
x4
|
x5
|
x6
|
x7
|
x8
|
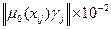
при  из из
табл. 5.1
 из табл. 5.3 из табл. 5.3
и все xij
={1}.
|
A1
A2
A3
A4
|
20 |
8 |
15 |
10 |
| 15 |
10 |
5 |
12 |
20
|
15 |
25 |
12 |
| 20 |
25 |
12 |
5 |
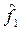 – мажоранта при – мажоранта при

|
20 |
15 |
12 |
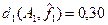 , ,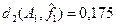 |
0 |
8 |
0 |
10 |
0 |
0 |
12 |
0 |
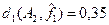 , ,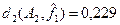 |
20 |
0 |
0 |
10 |
5 |
0 |
0 |
0 |
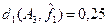 , , |
0 |
0 |
0 |
0 |
0 |
25 |
0 |
0 |
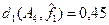 , ,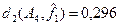 |
0 |
0 |
15 |
0 |
0 |
25 |
0 |
5 |
 – средняя при – средняя при

|
15 |
2 |
11,25 |
5 |
1,25 |
12,5 |
9 |
1,25 |
 , , |
5 |
6 |
3,75 |
5 |
1,25 |
12,5 |
9 |
1,25 |
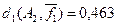 , , |
15 |
2 |
3,75 |
5 |
3,75 |
12,5 |
3 |
1,25 |
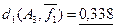 , ,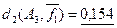 |
5 |
2 |
3,75 |
5 |
1,25 |
12,5 |
3 |
1,25 |
 , ,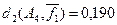 |
5 |
2 |
11,25 |
5 |
1,25 |
12,5 |
3 |
3,75 |
Таблицы 5.5 и 5.6 рассчитаны при введении в метрику и весовых коэффициентов и уровней характеристик систем, соответственно при целочисленных значениях x показателей принадлежности и достаточно произвольной выборки на отрезке [0,1]. В последнем случае оговорка «достаточно» связана с тем, что набор показателей принадлежности ограничивался близостью к установленным их значениям в табл. 5.1, в остальном же, осуществлялся произвольно.
Данные в табл. 5.5 и 5.6 показывают существенное влияние вводимых характеристик на близость к функциям 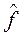 и и 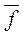 , соответствующих метрик. , соответствующих метрик.
Таблица 5.5
 Свойства Свойства
Системы
|
x1
|
x2
|
x3
|
x4
|
x5
|
X6
|
x7
|
X8
|

при 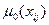 из из
табл. 5.1
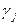 и и  из табл. 5.3 из табл. 5.3
|
A1
A2
A3
A4
|
180 |
64 |
90 |
60 |
| 90 |
70 |
40 |
108 |
40
|
45 |
225 |
96 |
| 120 |
150 |
72 |
10 |
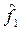 – мажоранта при – мажоранта при

|
180 |
90 |
108 |
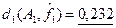 , , |
0 |
64 |
0 |
60 |
0 |
0 |
108 |
0 |
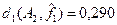 , , |
180 |
0 |
0 |
70 |
40 |
0 |
0 |
0 |
 , ,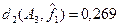 |
140 |
0 |
45 |
0 |
0 |
225 |
12 |
0 |
 , ,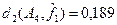 |
60 |
0 |
90 |
0 |
0 |
150 |
36 |
10 |
 – средняя при – средняя при

|
85 |
16 |
56,25 |
32,5 |
10 |
93,75 |
69 |
2,5 |
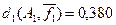 , ,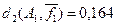 |
95 |
48 |
33,75 |
27,5 |
10 |
93,75 |
69 |
2,5 |
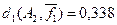 , ,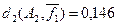 |
85 |
16 |
33,75 |
37,5 |
30 |
93,75 |
39 |
2,5 |
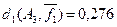 , ,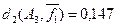 |
45 |
16 |
11,25 |
32,5 |
10 |
131,25 |
27 |
2,5 |
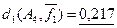 , ,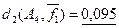 |
35 |
16 |
56,25 |
32,5 |
10 |
56,25 |
3 |
7,5 |
Таблица 5.6
 Свойства Свойства
Системы
|
x1
|
x2
|
x3
|
x4
|
x5
|
X6
|
x7
|
X8
|

при 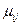 из из
табл. 5.2
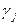 и и  из табл. 5.3 из табл. 5.3
|
A1
A2
A3
A4
|
108
|
51,2
|
63 |
36 |
5 |
7,5 |
2,4 |
1 |
4
|
1,6
|
90 |
63 |
36 |
7,5 |
75,6 |
2 |
24
|
6,4
|
31,5 |
2 |
2,5 |
180 |
86,4 |
12 |
| 72 |
6,4 |
4,5 |
2 |
4 |
120 |
64,8 |
10 |
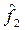 – мажоранта при – мажоранта при
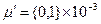
|
90 |
36 |
180 |
86,4 |
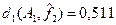 , ,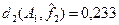 |
108 |
51,2 |
27 |
36 |
31 |
172,5 |
84 |
1 |
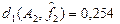 , ,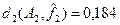 |
4 |
1,6 |
0 |
63 |
0 |
172,5 |
10,8 |
2 |
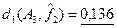 , ,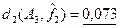 |
24 |
6,4 |
58,5 |
2 |
33,5 |
0 |
0 |
12 |
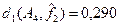 , ,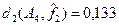 |
72 |
6,4 |
85,5 |
2 |
32 |
60 |
21,6 |
10 |
 – средняя при – средняя при

|
52 |
16,4 |
47,25 |
25,75 |
11,875
|
78,75 |
57,3 |
6,25 |
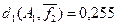 , ,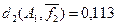 |
56 |
34,8 |
15,75 |
10,25 |
6,875 |
71,25 |
54,9 |
5,25 |
 , , |
48 |
14,8 |
42,75 |
37,25 |
24,125
|
71,25 |
18,3 |
4,25 |
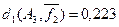 , ,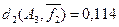 |
28 |
10,0 |
15,75 |
23,75 |
9,375 |
101,25
|
29,1 |
5,75 |
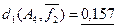 , ,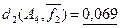 |
20 |
10,0 |
42,75 |
23,75 |
7,875 |
41,25 |
7,5 |
3,75 |
В тоже время общий обзор показывает:
– существование влияния показателя принадлежности (при принятой концепции построения его значений) – «притягивание» оценки к исходному случаю, к множеству A3
;
– среднее значение расстояний от предельных функций 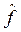 (~0,26) мало отличается от среднего расстояния от функции (~0,26) мало отличается от среднего расстояния от функции  (~0,23); (~0,23);
– линейная метрика d1
в среднем дает существенно большее отклонение от функций 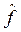 и и  (~0,32), чем евклидова метрика d2
(~0,17). (~0,32), чем евклидова метрика d2
(~0,17).
6. Классы и многообразия.
Термин класс
обычно употребляется в математике как синоним термина «множество» и, аналогично последнему, обозначает произвольные совокупности или признаки (например, в алгебре – классы эквивалентности относительно данного отношения эквивалентности).
Иногда классами предпочитают называть совокупности, элементами которых являются множества (например, в рекурсивной теории – перечислимые классы).
В аксиоматической теории множеств термин класс применяется для того, чтобы подчеркнуть, что данная совокупность оказывается собственно классом
, а не множеством в узком смысле (например, в алгебре – примитивные классы универсальных алгебр, называемые также многообразиями).
Перечислимые классы
– это классы, содержащие рекурсивно перечислимые множества. Примерами перечислимых множеств являются области значений вычислимых функций
, то есть функций, вычисление значений которых может быть проведено с помощью заранее заданной эффективной (реализуемой на машине Тьюринга) процедуры или алгоритма.
Примитивный класс универсальных алгебр
с системой операций W выделяется тем множеством тождественных соотношений  в них, которое выполняется всеми алгебрами этого класса. в них, которое выполняется всеми алгебрами этого класса.
Многообразие
в этом аспекте выступает как синоним понятия «примитивный класс», поскольку многообразие в общем случае интерпретируется, как совокупность объектов, наделенных некой структурой.
Таким образом, можно говорить о многообразии алгебраических систем
, как класса фиксированной сигнатуры W, аксиоматизируемого при помощи тождеств-формул вида
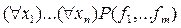 , ,
где P – какой-либо предикатный символ из W или знак равенства, а f1
,…,fm
– термы сигнатуры W от предметных переменных x1
,…,xn
.
Пример 5.12
. Примитивный класс (многообразие) составляют группы, рассматриваемые как алгебры с одной бинарной, одной унарной и одной нульарной операциями
G= < A; (•), µ, e>.
Здесь W={(•), µ, e} – сигнатура операций, где:
(•) – бинарная операция;
µ – обозначение унарной операции «обратный элемент»;
e – нульарная операция «сигнатурная единица».
В данном случае многообразие включает группу:
<R¢
; *, -1
, 1> – множество отличных от нуля действительных чисел R¢
с обычным умножением *, обращением –1
и числом 1 в качестве нейтрального элемента;
<R;Å, «–«, 0> – множество действительных чисел R, бинарная операция сложения Å, «–« унарная операция образования отрицательных чисел, 0 – нейтральный элемент;
<Mn
,
n
; *, -1
, In
,
n
> – множество квадратных матриц Mn
,
n
, бинарная операция умножения *, унарная операция обращения матрицы –1
, In
,
n
– единичная матрица;
<Sn
; *, -1
, e> – алгебра подстановок (см. §2.2, п. 4)
и тому подобные.
Система тождеств:
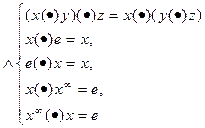 , ,
выполняется в каждой из приведенных в примере алгебр. Таким образом, эти алгебры входят в  -многообразие групп. -многообразие групп.
Отметим, что если система тождеств  будет дополнена тождественным соотношением x(•)y=y(•)x, то выделяется будет дополнена тождественным соотношением x(•)y=y(•)x, то выделяется  -многообразие абелевых групп более узкое в сравнении с -многообразие абелевых групп более узкое в сравнении с  -многообразием. -многообразием.
Из приведенных в примере 5.12 групп, только группы R¢
и R являются абелевыми.
Если будут использованы другие дополнительные тождества, то многообразие будет сужаться почти всегда.
Кольца, ассоциативные кольца, ассоциативно-коммутативные кольца и другие этого же рода алгебры составляют соответствующие многообразия.
7. Категории и функторы.
При рассмотрении множеств с некоторым строением и с некоторыми отображениями между ними, которые сохраняют данное строение; глобальных межсистемных связей и т. п., – нередко обычные алгебраические средства оказываются недостаточными. Полезным дополнением к ним во многих случаях могут служить конструкции и методы теории категорий, привлекающей все большее внимание в различных прикладных областях.
Категория
К
состоит из объектов
(ОbК
) и морфизмов (
MorK
)
, связанных следующими условиями:
1
. Каждый морфизм aÎMorK
приписан к некоторой единственной для него упорядоченной паре объектов (A, B), При этом, как и ранее, пишут a:A®B или 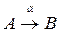 . Объект A называют началом
или областью определения
морфизма a, а объект – его концом
или областью значений
. . Объект A называют началом
или областью определения
морфизма a, а объект – его концом
или областью значений
.
Множество всех морфизмов, приписанных к данной паре объектов (A, B) обозначают Hom(A, B), HK
(A, B) или H(A, B).
2
. Для любых морфизмов a:A®B и b:B®C (aÎH(A,B) и bÎH(B,C)) определено их произведение
ab, причем abÎH(A, C), называемое также композицией
.
3
. Если задана a:A®B, b:B®C и g:C®D так, что (ab)g и a(bg), определены, то равенство
(ab)g=a(bg) (5.9)
отражает ассоциативность произведения морфизмов.
4
. Для любого объекта A существует морфизм 1
A
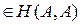 такой, что 1
A такой, что 1
A
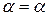 и и 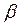 1
A
= 1
A
=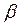 для любых a:A®B и b:C®A. Морфизм 1
A
называется тождественным
или единичным
на A. для любых a:A®B и b:C®A. Морфизм 1
A
называется тождественным
или единичным
на A.
Из этих определений следует, что H(A, A) для любых объектов A является моноидом.
Пример 5.13
. Категория St
, которую образуют все множества в данном универсуме и все отображения между ними, включая для каждого множества A отображение Æ®A, определяемое пустой функцией Æ.
Пустое множество Æ является левым нулем
(инициальным объектом
), а одноэмментное множество правым нулем
(терминальным объектом
). Всякое непустое множество является образующим объектом. Всякий мономорфизм с непустым началом есть обратимое справа
инъективное отображение, всякий эпиморфизм есть обратимое слева
сюръективное отображение.
Нулевой объект категории
– такой объект (обозначаемый обычно 0), что для каждого объекта X этой категории множества H(X, 0) и H(0, X) одноэлементные.
Если в категории с нулем через w0
X
обозначить единственный морфизм в H(0, X), через wX
0
– единственный морфизм в H(X, 0), то нулевой морфизм
из A в B определится равенством
wAB
=wA0
w0B
(5.10).
Из свойств категории St
следует, что H(A, B) есть не что иное, как совокупность всех функций, заданных на A и принимающих значения в множестве B. Таким, образом, wAB
=f(x1
,…,xn
)=0 – нуль-функция
. Тождественный морфизм 1
B
– это тождественная функция
fA
:A®A, а произведение морфизмов f:A®B, g:B®C совпадает с обычной суперпозицией функции f0
g.
Соответствие между любыми категориями K
1
и K
2
выражается функтором, – понятием, в определенном смысле, подобном понятию функции.
Функтор
– отображение одной категории в другую. При этом имеется в виду пара отображений:
ObK
1
в ObK
2
иHomK
1
в HomK
2
,
для простоты обозначаемых одной и той же буквой, например F и удовлетворяющие следующим условиям:
1) если aÎH(A,B), то F(a)ÎH(F(A),F(B));
2) если aÎH(A,B) и bÎH(B,C), F (ab)=F(a)F(b);
3) F(1
X
)=1
F(X) для любого объекта X из K
.
Для любой категории K
отображение A®A,a®a отображает тождественный функтор
этой категории на себя.
Отображение F:K
®
K
¢
категории K
в категорию K
¢
называется ковариантным функтором
, если для каждого объекта AÎObK объект F(A) ÎObK¢
, для каждого морфизма aÎHK
(A, B) образ F(a)Î (F(A), F(B)), причем F(1
A
)=1
F(A) и F(ab)=F(a)´F(b) всякий раз, когда определено произведение ab. (F(A), F(B)), причем F(1
A
)=1
F(A) и F(ab)=F(a)´F(b) всякий раз, когда определено произведение ab.
Функтор из категории K
в категорию множеств St
, сопоставляющий каждому K-объекту X множество FP
(X)=H(P, X), а каждому морфизму b:X®Y – отображение FP
(b):F(X)®F(Y), a®ab, называется основным функтором
. С последним определением связано понятие проективного объекта. Объект Pпроективен
, если основной функтор FP
переводит эпиморфизмы категории St
.
Каждой категории K
может быть сопоставлена двойственная (дуальная) категория K
*
, для которой ObK
*
=ObK
и
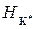 (A, B)=HK
(B, A) длялюбых A, BÎObK. (A, B)=HK
(B, A) длялюбых A, BÎObK.
Возникает понятие контрвариантного функтора
из K
в K
¢
, под которым понимается ковариантный функтор из K
*
в K
¢
. Отметим так же, что наряду с функтором одного аргумента можно рассматривать и функторы многих аргументов.
Для каждого предложения теории категорий существует двойственное (дуальное) предложение. При этом справедлив принцип двойственности
: предложение p истинно в теории категорий тогда и только тогда, когда в этой теории истинно двойственное предложение p*
.
Многие понятия в математике с категорной точки зрения являются двойственными друг другу: инъективность – проективность, многообразия и радикалы в алгебре и т. д. .
Актуальными в плане теории дискретных структур являются также категории, рассмотренные ниже.
Пример 5.14
. Категория Alg
(t) всех алгебр данного типа t и их гомоморфизмов. Если A
и B
– две алгебры типа t, то Hom(A, B) – это совокупность всех гомоморфизмов алгебры A
в алгебру B
, а 1
A
– тождественный автоморфизм DA
алгебры A
.
Категория 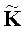 называется подкатегорией
K
, если каждый называется подкатегорией
K
, если каждый 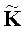 -объект является K
-объектом, каждый -объект является K
-объектом, каждый 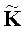 -морфизм является K
-морфизмом, тождественные -морфизм является K
-морфизмом, тождественные 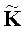 -морфизмы тождественны в K
и произведение -морфизмы тождественны в K
и произведение 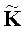 -морфизмов тоже, что и в K
. -морфизмов тоже, что и в K
.
Например, структуры и структурные гомоморфизмы образуют подкатегорию Str
категории St
Ù
упорядоченных множеств и гомоморфизмов между ними, а категория Boole
-
A
булевых алгебр и их гомоморфизмов будет подкатегорией категории Alg
(2, 2. 1, 0, 0).
Пример 5.15
. Натурально нумерованные множества M образуют категорию St
N
, в которой они выступают в роли объектов MÎObStN
. Морфизмом из натурально нумерованного множества M1
(с нумерацией m1
) в натурально нумерованное множество M2
(с нумерацией m2
) называется отображение a: M1
®M2
, для которого существует всюду определенная на N вычислимая функция f такая, что
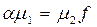 (5.11) (5.11)
(см. в частности, п. 1 настоящего параграфа).
Категория St
N
множеств натуральной нумерации является подкатегорией категории St
S
, образованной всеми нумерованными множествами, а не только натурально нумерованными.
*
Клон операции – всякое замкнутое относительно композиции множество конечномерных операций вида w: Аn
® А, содержащее все единичные операции 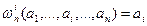 для любого набора для любого набора 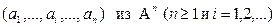 . Композиция
– операция вида . Композиция
– операция вида  , где для множеств C,U и Z ={z1
,…, zl
} выполнено , где для множеств C,U и Z ={z1
,…, zl
} выполнено  . .
|