МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ „ЛЬВІВСЬКА ПОЛІТЕХНІКА”
Кафедра теоретичної радіотехніки та радіовимірювань
Курсова робота з дисципліни
“Теорія електричного зв'язку”
На тему:
Розрахунок та оптимізація характеристик дискретної системи електрозв'язку
Львів 2006
ЗМІСТ
Завдання на курсову роботу
Вступ
1. Структурна схема системи передачі
2. Розрахунок параметрів кодера і декодера простого коду
3. Розрахунок інформаційних характеристик джерела повідомлень
4. Розрахунок завадостійкості демодулятора
5. Вибір коду, що коректує, і розрахунок завадостійкості системи зв'язку з кодуванням
6. Розрахунок ефективності системи передачі дискретних повідомлень
Висновок
Перелік посилань
ВСТУП
Життя сучасного суспільства немислиме без широко розгалужених систем передачі інформації. Без них не змогли би функціонувати промисловість, сільське господарство, транспорт. Зокрема широке розповсюдження мають дискретні системи передачі. Найбільш поширеним прикладом дискретної системи передачі є система телеграфії, в якій як інформація використовується послідовність знаків ─ букв і цифр. Як відомо дискретні повідомлення є дискретні в часі і по рівнях.
Дискретні і цифрові системи передачі знаходять широке розповсюдження через їх величезні переваги над аналоговою системою. Найбільшою перевагою їх є висока завадостійкість, дешева передавальна і приймальна апаратура, і висока якість передачі інформації. В аналоговій системі передач сигнал передається у аналоговому вигляді в більшості випадків з перенесенням спектру сигналу у вищі частоти. Відмінністю дискретної системи передачі від цифрової є те, що в цифровій системі джерело інформації видає повідомлення в аналоговому вигляді, а потім відбувається дискретизація по часу і квантування по рівнях. Подальший процес передачі співпадає в обох системах передачі. Отже відмінністю дискретної системи передачі від цифрової є наявність дискретного джерела повідомлень в дискретній. Основними параметрами дискретного джерела повідомлень є ентропія, коефіцієнт надлишковості і продуктивність, які разом з імовірністю помилки на виході декодера визначають ефективність системи передачі. Повідомлення дискретного джерела кодується двійковим кодом і передається дискретним каналом зв'язку з завадостійким кодуванням. Для передачі неперервним каналом зв'язку з постійними параметрами і адитивним білим гаусовим шумом використовується модуляція гармонійного переносника. Дана курсова робота призначена для дослідження дискретної системи передачі, її основних параметрів, а також вибору коректуючого коду для пониження необхідного відношення сигнал – шум, для забезпечення необхідної імовірності помилки на виході декодера, тобто правильної передачі сигналу.
ЗАВДАННЯ НА КУРСОВУ РОБОТУ
Варіант Д ─ 28
Номер
варіанту
|
Джерело
повідомлень
|
Рзн
|
В,
Бод
|
Метод
модуляції
|
Спосіб
прийому
|
ЕВК,
дБ
|
| Д-28 |
Ma
=128 |
4Е-6 |
300 |
ЧМ-2 |
когерент. |
1.45 |
Наведені вихідні дані:
1. Джерело виробляє послідовність незалежних знаків з розподілом імовірностей: або рівноймовірним при об'ємі алфавіту М
а
, або з розподілом букв українського тексту, або з розподілом букв російського тексту, або з розподілом букв англійського тексту.
2. Допустима ймовірність помилки знаку на вході одержувача Р
зн
.
3. Швидкість модуляції на виході кодера простого коду В.
4. Метод модуляції.
5. Спосіб прийому: когерентний або некогерентний.
6. Енергетичний виграш кодування (ЕВК).
Завдання
1. Структурна схема СПДП
. Зобразити структурну схему системи передачі дискретних повідомлень. Пояснити призначення кожного блоку, дати визначення основних параметрів, що характеризують кожний блок, і навести часові діаграми характерних сигналів на входах і виходах блоків.
2. Розрахунок параметрів кодера і декодера простого коду
. Розрахувати параметри кодера і декодера простого коду: довжину коду n
, тривалість двійкового символу Т
б
, час передачі одного знаку Т
зн
, допустиму ймовірність помилки символу на вході декодера р
б
.
3. Розрахунок інформаційних характеристик джерела повідомлень
. Для заданих статистичних характеристик джерела дискретних повідомлень виконати розрахунок ентропії Н
(А
), надмірності ? і продуктивності джерела R
д
. Пояснити причини надмірності джерела. Сформулювати вимоги до пропускної здатності каналу зв'язку.
4. Розрахунок завадостійкості демодулятора
. Для заданих методу модуляції і способу прийому розрахувати і побудувати графік залежності ймовірності помилки двійкового символу на виході демодулятора від відношення сигнал/шум на вході демодулятора р
= f
(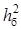 ); визначити необхідне відношення сигнал/шум на вході демодулятора ); визначити необхідне відношення сигнал/шум на вході демодулятора 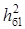 , при якому ймовірність помилки символу на виході демодулятора дорівнює допустимій ймовірності помилки символу на вході декодера простого коду р
б
. , при якому ймовірність помилки символу на виході демодулятора дорівнює допустимій ймовірності помилки символу на вході декодера простого коду р
б
.
5. Вибір коректуючого коду і розрахунок завадостійкості системи зв'язку з кодуванням
. Для заданих методу модуляції і способу прийому вибрати коректуючий код, що забезпечує заданий енергетичний виграш кодування при ймовірності помилки символу на виході декодера р
д
= p
б
. Розрахувати і побудувати залежність ймовірності помилки символу на виході декодера від відношення сигнал/шум на вході демодулятора p
д
= f
1
(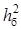 ). Визначити необхідне відношення сигнал/шум на вході демодулятора ). Визначити необхідне відношення сигнал/шум на вході демодулятора 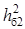 , при якому забезпечується ймовірність помилки символу на виході декодера р
б
. Визначити досягнутий ЕВК. , при якому забезпечується ймовірність помилки символу на виході декодера р
б
. Визначити досягнутий ЕВК.
6. Розрахунок ефективності системи передачі дискретних повідомлень
. Виконати розрахунки і порівняння інформаційної, енергетичної і частотної ефективності системи зв'язку, що розраховується, для двох варіантів передачі – з завадостійким кодуванням і без нього. Побудувати графік граничної залежності b=f
(g). На цьому рисунку точками відбити ефективність двох варіантів передачі. Порівняти ефективність двох варіантів передачі між собою і з граничною ефективністю. Зробити висновки за результатами порівняння.
7. Заключення
. Зробити висновки по курсовій роботі в цілому.
1. СТРУКТУРНА СХЕМА СИСТЕМИ ПЕРЕДАЧІ ПОВІДОМЛЕНЬ
Структурна схема системи передачі дискретних повідомлень представлена на рис.1.

Рис.1
Джерело повідомлень ─ це людина і технічні об’єкти (інформаційні системи, комп’ютери) , яке видає відомості про різноманітні процеси (фізичні суспільні), про характеристики та параметри досліджуваних об’єктів, що їх використовують у практичній діяльності. Джерело дискретних повідомлень генерує сигнали через певні проміжки часу і сигнал може приймати тільки певні визначені відліки (рис. 2а).Прикладом таких повідомлень можуть бути букви, цифри, тощо. Параметрами джерела є ентропія Н
, надлишковість 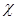 , продуктивність R
. Кодер простого коду ─ пристрій кодування, який ставить у відповідність кожному відліку інформаційного сигналу певну кодову комбінацію. На вхід подається дискретний сигнал, а на виході отримується цифровий сигнал, який представляє квантовані відліки інформаційного сигналу кодовими комбінаціями вибраного коду. Всі кодові комбінації використовуються для передачі повідомлень. Основним параметром є розрядність коду k
. Цифровий сигнал представляється у вигляді послідовності двійкових імпульсів (рис. 2б). Кодер коректуючого коду підвищує завадостійкість системи передачі за допомогою використання завадостійких кодів, що здатні виявляти і виправляти помилки. Завадостійкі коди будуються так, що для передачі повідомлення використовуються не всі кодові комбінації, а лише деяка їх частина. Тим самим створюється можливість виявлення та виправлення помилки при неправильному прийомі деякого числа символів. Коректуючі якості кодів досягаються введенням в кодові комбінації додаткових(перевірочних, надлишкових) розрядів (рис. 2в). Параметрами кодера коректую чого коду є загальна кількість розрядів n
, кількість інформаційних розрядів k
, кількість розрядів у перевірочній частині кодової комбінації m
і кількість помилок в розрядах які код здатен виправити qвипр
.
. Модулятор ─ це пристрій який здійснює модуляцію, тобто вкладання інформаційного сигналу в сигнал-перенощик (гармонічний сигнал, який виконує функцію перенощика енергії в радіоефірі).Він призначений для узгодження інформаційного сигналу з лінією зв’язку. Загальний принцип модуляції полягає в зміні одного чи декількох параметрів несучого коливання f(a,b,…,t) в згідності з повідомленням. Для цифрового сигналу модуляція називається маніпуляцією. У нашому випадку застосовується гармонічний сигнал перенощик і ЧМ маніпуляція (“1” передається з частотою f1
“0” – з f0
, f1
>f0
) (рис. 2г). Канал зв’язку ─ складається з пристрою вводу в канал зв’язку, лініЇ зв’язку з джерелом завад та пристрою виводу з каналу зв’язку. Для каналів зв’язку характерні статичні, енергетичні та частотні параметри;первинні та вторинні параметри. До первинних відносяться: ймовірність правильної передачі сигналу; ймовірність помилки при передачі сигналу; ймовірність стирання сигналу. Якість каналу зв’язку можна оцінити за такими вторинними параметрами: ймовірність повної помилки при передачі сигналів; ймовірність поравильного прийому в кількох пунктах одночасно. Проте найважливішими є інформаційні параметри каналів зв’язку: пропускна здатність каналів зв’язку С
; швидкість передачі інформації по каналу зв’язку В
. В каналі діють завади у вигляді білого гауссівського шуму. В результаті виникає спотворення сигналу (рис. 2д). Демодулятор призначений для виділення інформаційного сигналу з коливання. Сигнал відновлюється з деякою похибкою (рис. 2в). Декодер коду що коректує, здійснює виправлення або виявлення помилок, перетворює кодову комбінацію у комбінацію простого коду (рис. 2б). Декодер простого коду перетворює кодову комбінацію у відліку інформаційного сигналу (рис. 2а). Одержувач отримує передану інформацію. , продуктивність R
. Кодер простого коду ─ пристрій кодування, який ставить у відповідність кожному відліку інформаційного сигналу певну кодову комбінацію. На вхід подається дискретний сигнал, а на виході отримується цифровий сигнал, який представляє квантовані відліки інформаційного сигналу кодовими комбінаціями вибраного коду. Всі кодові комбінації використовуються для передачі повідомлень. Основним параметром є розрядність коду k
. Цифровий сигнал представляється у вигляді послідовності двійкових імпульсів (рис. 2б). Кодер коректуючого коду підвищує завадостійкість системи передачі за допомогою використання завадостійких кодів, що здатні виявляти і виправляти помилки. Завадостійкі коди будуються так, що для передачі повідомлення використовуються не всі кодові комбінації, а лише деяка їх частина. Тим самим створюється можливість виявлення та виправлення помилки при неправильному прийомі деякого числа символів. Коректуючі якості кодів досягаються введенням в кодові комбінації додаткових(перевірочних, надлишкових) розрядів (рис. 2в). Параметрами кодера коректую чого коду є загальна кількість розрядів n
, кількість інформаційних розрядів k
, кількість розрядів у перевірочній частині кодової комбінації m
і кількість помилок в розрядах які код здатен виправити qвипр
.
. Модулятор ─ це пристрій який здійснює модуляцію, тобто вкладання інформаційного сигналу в сигнал-перенощик (гармонічний сигнал, який виконує функцію перенощика енергії в радіоефірі).Він призначений для узгодження інформаційного сигналу з лінією зв’язку. Загальний принцип модуляції полягає в зміні одного чи декількох параметрів несучого коливання f(a,b,…,t) в згідності з повідомленням. Для цифрового сигналу модуляція називається маніпуляцією. У нашому випадку застосовується гармонічний сигнал перенощик і ЧМ маніпуляція (“1” передається з частотою f1
“0” – з f0
, f1
>f0
) (рис. 2г). Канал зв’язку ─ складається з пристрою вводу в канал зв’язку, лініЇ зв’язку з джерелом завад та пристрою виводу з каналу зв’язку. Для каналів зв’язку характерні статичні, енергетичні та частотні параметри;первинні та вторинні параметри. До первинних відносяться: ймовірність правильної передачі сигналу; ймовірність помилки при передачі сигналу; ймовірність стирання сигналу. Якість каналу зв’язку можна оцінити за такими вторинними параметрами: ймовірність повної помилки при передачі сигналів; ймовірність поравильного прийому в кількох пунктах одночасно. Проте найважливішими є інформаційні параметри каналів зв’язку: пропускна здатність каналів зв’язку С
; швидкість передачі інформації по каналу зв’язку В
. В каналі діють завади у вигляді білого гауссівського шуму. В результаті виникає спотворення сигналу (рис. 2д). Демодулятор призначений для виділення інформаційного сигналу з коливання. Сигнал відновлюється з деякою похибкою (рис. 2в). Декодер коду що коректує, здійснює виправлення або виявлення помилок, перетворює кодову комбінацію у комбінацію простого коду (рис. 2б). Декодер простого коду перетворює кодову комбінацію у відліку інформаційного сигналу (рис. 2а). Одержувач отримує передану інформацію.

а

б

в

Г

д
Рис.2
2. РОЗРАХУНОК ПАРАМЕТРІВ КОДЕРА І ДЕКОДЕРА ПРОСТОГО КОДУ
Вихідні дані:
- об'єм алфавіту джерела дискретних повідомлень М
а
= 128;
- швидкість модуляції на виході кодера простого коду В
= 300 Бод;
- допустима ймовірність помилки знаку на виході декодера Р
зн
= 4е-6.
Вимагається визначити:
- тривалість двійкового символу (біта) на виході кодера Т
б
;
- довжину простого коду n
;
- час передачі одного знаку Т
зн
;
- допустиму ймовірність помилки біта на вході декодера р
б
.
Розрахункові співвідношення й порядок розрахунку
Припускаємо, що кодування ведеться рівномірним кодом, при якому, на відміну від нерівномірного коду, більш прості в реалізації кодер та декодер.
Довжина коду визначається за умови, що число можливих комбінацій не менш за об'єм алфавіту джерела
2n
³ М
a
або n
³ log2
M
a
.(2.1)
n
³ log2
128, n
³ 7.
Оскільки інші вимоги до коду не пред'являються, то довжина коду вибирається як мінімальне ціле число, при якому виконуються нерівності (3.1). Тривалість двійкового символу на виході кодера визначається
Т
б
= 1/В.
Т
б = 1/300=3,333∙10-3
с. (2.2)
= 1/300=3,333∙10-3
с. (2.2)
Час передачі одного знаку
Т
зн
= nT
б
.(2.3)
Т
зн
= nT
б
=7∙3,333∙10-3
=0,023 с.
Допустима ймовірність помилки біта на вході декодера визначається за умови, що помилки символів в каналі зв'язку (вихід кодера – вхід декодера) незалежні: Р
зн
= 1 – (1 – р
б
) n
= 1 – (1 – np
б
+ 0,5n(n–1)p
б
2
– ... ). Ясно, що при заданих малих значеннях Р
зн
£ 10–4
величина Р
зн
буде визначатись складовим np
б
, тобто
Р
б
= Р
зн
/n
.(2.4)
Р
б
= Р
зн
/n
=4∙10-6
/7=5,714∙10-7
.
3 РОЗРАХУНОК ІНФОРМАЦІЙНИХ ХАРАКТЕРИСТИК ДЖЕРЕЛА ДИСКРЕТНИХ ПОВІДОМЛЕНЬ
Вихідні дані:
- обсяг алфавіту джерела М
a
=128;
- тривалість передачі одного знаку Т
зн
= 0,023 с.
Вимагається розрахувати:
- ентропію джерела Н
(А)
;
- коефіцієнт надлишковості джерела ?;
- продуктивність джерела R
д
.
Розрахункові формули і порядок розрахунку
Ентропія ─ середнє значення інформації, яке припадає на одне повідомлення джерела.
Н
(А)
= 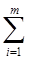 P(ai
)∙log2
1/P(ai
)(3.1) P(ai
)∙log2
1/P(ai
)(3.1)
Але оскільки ймовірність появи всіх символів однакова то ентропія джерела дорівнює максимальній ентропії, що обчислююється за формулою:
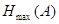 = log2
m(3.1а) = log2
m(3.1а)
Надлишковість − характеризує вагу інформації джерела, яку можна передавати і при цьому втрат інформації не буде. Другими словами надлишковість це є несуттєва інформація джерела. Вона розраховується за формулою:
? = 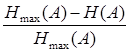 (3.2) (3.2)
Продуктивність джерела R
д
− це швидкість появи інформації на виході джерела дискретних повідомлень.
R
д
= Hmax
(A)/Tзн
(3.3)
З формули 3.1 обчислюємо ентропію (ймовірності появи символів вказані в таблиці 1):
Н
(А)
= log2
128 = 7;
З формули 3.2 знаходимо надлишковість:
? = (7 – 7)/7 = 0;
Продуктивність джерела знаходимо за формулою 3.3:
R
д
=7/0,023= 300 біт/с.
Вимоги до пропускної здатності дискретного каналу зв'язку формулюються на основі теореми кодування Шеннона: якщо продуктивність джерела повідомлень менша пропускної здатності каналу С, то існує спосіб кодування і декодування, при якому ймовірність помилкового декодування і ненадійність можуть бути як завгодно малі. Якщо ж R
д
> C, то таких способів не існує.
4. РОЗРАХУНОК ЗАВАДОСТІЙКОСТІ ДЕМОДУЛЯТОРА
Вихідні дані:
- метод модуляції та спосіб прийому – ЧМ – 2 когерентний;
- канал зв'язку – з постійними параметрами і адитивним білим гауссовим шумом;
- допустима ймовірність помилки двійкового символу (біта) в каналі р
б
= 5,714∙10-7
;
- тривалість двійкового символу Т
б
= 3,333∙10-3
с.
Вимагається розрахувати:
- залежність імовірності помилки біта від відношення сигнал/шум на вході демодулятора р
= f
(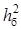 ) та побудувати графік цієї залежності; ) та побудувати графік цієї залежності;
- значення необхідного відношення сигнал/шум на вході демодулятора 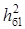 , що забезпечує допустиму ймовірність помилки біта р
б
. , що забезпечує допустиму ймовірність помилки біта р
б
.
Розрахункові співвідношення
Завадостійкість демодулятора сигналу дискретної модуляції визначають імовірністю помилки елементу модульованого сигналу Р
пом
або імовірністю помилки двійкового символу р
. Імовірності помилки Р
пом
і р
залежать від методу модуляції, способу прийому, відношення середньої енергії сигналів до питомої потужності завади та характеристик каналу зв'язку.
р
= 0,5∙(1 – Ф(х))(4.1)
де Ф(х) = 1 – 1,3∙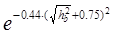
Формула 4.1 визначає імовірність помилки двійкового символу при передачі багатопозиційними сигналами по гауссовому каналу зв'язку з постійними параметрами. Перерахунок імовірності помилки елементу модульованого сигналу Р
пом
в імовірність помилки двійкового символу р
було зроблено в припущенні, що використовується маніпуляційний код Грея.
В усіх формулах прийняті позначення:
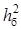 =E
б
/N
0
- відношення середньої енергії сигналів, що витрачається на передачу одного двійкового символу, до питомої потужності шуму; =E
б
/N
0
- відношення середньої енергії сигналів, що витрачається на передачу одного двійкового символу, до питомої потужності шуму;
E
б
=PS
Т
б
;
PS
- середня потужність сигналу.
Для двійкових сигналів значення Р
пом
і р
співпадають.
Виконання розрахунків
Для заданого виду модуляції та способу прийому розраховуємо і будуємо графік залежності р
= f
(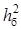 ). При побудові графіка масштаб для р
логарифмічний, а для значень ). При побудові графіка масштаб для р
логарифмічний, а для значень 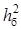 , виражених у децибелах ( , виражених у децибелах (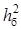 [дБ] = 10lg [дБ] = 10lg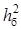 ), – лінійний. При розрахунках збільшуємо ), – лінійний. При розрахунках збільшуємо 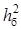 з кроком 2 дБ, починаючи з 2 дБ, до того, як р
не виявиться менш значення р
б
. з кроком 2 дБ, починаючи з 2 дБ, до того, як р
не виявиться менш значення р
б
.
Таблиця 4.1 ─ Залежність імовірності помилки біта від відношення сигнал/шум
| h2
б1
, дБ |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
| h2
б1
, рази |
1,585 |
2,512 |
3,981 |
6,3010 |
10 |
15,849 |
25,119 |
39,811 |
| P |
0,11 |
0,059 |
0,024 |
6,02 E-03 |
7,73E-04 |
3,43E-05 |
2,95E-07 |
1,95E-10 |

Рисунок 4.1 ─ Завадостійкість системи передачі без завадостійкого кодування
Якщо в каналі зв'язку не використовується завадостійке кодування, то допустима ймовірність помилки символу на виході демодулятора дорівнює значенню р
б
, знайденому при розрахунку параметрів ЦАП або декодера простого коду. З рисунка 4.1 визначаємо необхідне відношення сигнал/шум для системи передачі без кодування 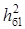 , при якому р
= р
б
. , при якому р
= р
б
.
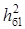 =13,75 дБ. =13,75 дБ.
5 ВИБІР КОРЕКТУЮЧОГО КОДУ І РОЗРАХУНОК ЗАВАДОСТІЙКОСТІ СИСТЕМИ ЗВ'ЯЗКУ З КОДУВАННЯМ
Вихідні дані для розрахунку:
- необхідний ЕВК = 1,45 дБ;
- метод модуляції в каналі зв'язку і спосіб прийому – ЧМ – 2 когерентний;
- тип неперервного каналу зв'язку – з постійними параметрами та адитивним білим гауссовим шумом;
- допустима ймовірність помилки двійкового символу на виході декодера p
б
= 5,714∙10-7
;
- відношення сигнал/шум на вході демодулятора 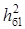 =13,75 дБ, що забезпечує допустиму ймовірність помилки р
б
= 5,714∙10-7
в каналі без завадостійкого кодування; =13,75 дБ, що забезпечує допустиму ймовірність помилки р
б
= 5,714∙10-7
в каналі без завадостійкого кодування;
- тривалість двійкового символу на вході кодера коректуючого коду Т
б
= 3,333∙10-3
с.
Вимагається:
- вибрати і обгрунтувати параметри коду, що забезпечує необхідний ЕВК: довжину коду n
, число інформаційних символів k
і кратність виправлюваних помилок qв
;
- розрахувати залежність імовірності помилки символу на виході декодера від відношення сигнал/шум на вході демодулятора р
д
=f1
(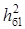 ) при використанні вибраного коду; ) при використанні вибраного коду;
- визначити одержаний ЕВК та порівняти його з необхідним.
Розрахункові співвідношення
Коректуючі коди дозволяють підвищити завадостійкість і завдяки цьому зменшити необхідне відношення сигнал/шум на вході демодулятора при заданій імовірності помилки прийнятих символів. Величина, що показує в скільки разів (на скільки децибел) зменшується необхідне відношення сигнал/шум на вході демодулятора, завдяки використанню кодування, називається енергетичним виграшем кодування (ЕВК).
Канали зв'язку з завадостійким кодуванням і без нього зручно порівнювати, якщо в якості відношення сигнал/шум використати відношення середньої енергії сигналів, що витрачається на передачу одного інформаційного символу, до питомої потужності шуму 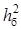 =РS
Tб
/N0
. =РS
Tб
/N0
.
Так, якщо в каналі зв'язку без кодування необхідне відношення сигнал/шум для забезпечення заданої ймовірності помилки дорівнює 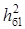 , а в каналі зв'язку з кодуванням – , а в каналі зв'язку з кодуванням – 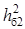 , то ЕВК буде визначатися , то ЕВК буде визначатися
D=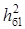 / /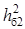 або в [дБ]= або в [дБ]=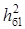 [дБ] – [дБ] –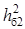 [дБ].(5.1) [дБ].(5.1)
При декодуванні з виправленням помилок імовірність помилкового декодування кодових комбінацій Р
пд
визначається за умови, що число помилок в кодовій комбінації на вході декодера q
перевищує кратність помилок, що виправляються q
в
:
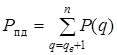 ,(5.2) ,(5.2)
де Р
(q)
=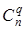 pq
(1 – p) n
- q
(5.3) pq
(1 – p) n
- q
(5.3)
– імовірність помилки кратності q
;
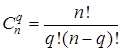 (5.4) (5.4)
– число сполучень із n
по q
;
р
– імовірність помилки двійкового символу на вході декодера, розрахунок якої для гауссового каналу зв'язку з постійними параметрами розглянутий в розд. 4. В використаних там формулах замість 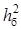 підставляємо підставляємо 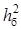 k
/n –
враховуючи зменшення тривалості символів із-за введення в кодові комбінації додаткових символів при кодуванні і відповідне зменшення енергії сигналу на вході демодулятора. k
/n –
враховуючи зменшення тривалості символів із-за введення в кодові комбінації додаткових символів при кодуванні і відповідне зменшення енергії сигналу на вході демодулятора.
Для переходу від ймовірності Р
пд
до ймовірності помилки двійкового символу на виході декодера р
д
достатньо врахувати принцип виправлення помилок декодером: декодер заборонену кодову комбінацію замінює найближчою дозволеною. Тому, якщо число помилок в комбінації q
> q
в
, але q
£ d
min
, то в результаті декодування комбінація буде містити d
min
помилок (d
min
– кодова віддаль). Оскільки помилки більш високої кратності малоймовірні, то остаточно можна вважати, що в помилково декодованій комбінації є d
min
помилкових символів. У коректуючих кодів кодова віддаль d
min
³ 2q
в
+ 1. Оскільки при помилковому декодуванні кодової комбінації 2q
в
+ 1 символ із n
помилковий, то перехід від Р
пд
до р
д
виконується за формулою
р
д
= Р
пд
(2q
в
+ 1)/n
.(5.5)
Зв'язок між основними параметрами двійкових коректуючих кодів n
, k
і q
в
встановлює верхня межа Хеммінга
2n – k
– 1 ³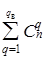 .(5.6) .(5.6)
Для досконалих кодів нерівність (5.6) переходить в рівність і при цьому мінімізується число додаткових символів n
– k
при фіксованих значеннях n
і q
в
. Широке розповсюдження дістали циклічні коди Боуза-Чоудхурі-Хоквінгема (БЧХ). За параметрами вони близькі до досконалих кодів і разом з тим вимагають відносно простих схем кодерів та декодерів. У кодів БЧХ основні параметри пов'язані співвідношеннями:
k
= n
– mq
в
,(5.7)
де m
– найменше ціле, при якому задовольняється нерівність-рівність
m
³ log2
(n + 1). (5.7a)
З формул (5.2) – (5.7) слідує, що завадостійкість у каналі зв'язку з кодуванням і ЕВК складним чином залежать від параметрів коду n
, k
і q
в
та відношення сигнал/шум 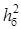 . Крім того, один і той же ЕВК може бути досягнутий при різних значеннях n
, k
і q
в
. . Крім того, один і той же ЕВК може бути досягнутий при різних значеннях n
, k
і q
в
.
Перевірка правильності вибору коду
Знайдені параметри коду n
, k
і q
в
слід розглядати як орієнтовні, і правильність вибору коду слід підтвердити розрахунками. Для цього необхідно розрахувати:
* необхідне відношення сигнал/шум на вході демодулятора в каналі зв'язку з завадостійким кодуванням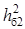 за формулою (5.1) за формулою (5.1)
D = 1,4;
* імовірність помилки символу на виході демодулятора р
за методикою, яка викладена в розд. 6.2, підставляючи замість 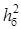 в формулу для розрахунку р
значення в формулу для розрахунку р
значення 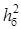 k
/n
; k
/n
;
* імовірність помилкового декодування кодової комбінації Р
пд
за формулами (5.2) – (5.4), у сумі в формулі (5.2) достатньо врахувати першу складову;
* імовірність помилки символу на виході декодера p
д
за формулою (5.5).
Робимо розрахунки для 2 кодів з різними параметрами. Результати розрахунків слід оформлюємо у вигляді таблиці, що містить значення q
в
, n
, k
, p
, P
пд
і р
д
.
Таблиця 5.1 ─ Залежність імовірності помилки символу від параметрів коду 1
| q |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
| n |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
23 |
| k |
18 |
18 |
18 |
18 |
18 |
18 |
18 |
18 |
| Pпд |
0,855 |
0,591 |
0,236 |
0,037 |
1,6Е10-03 |
1,131E-04 |
5,744E-09 |
5,092E-14 |
| Рд |
0,112 |
0,077 |
0,031 |
4,9Е10-03 |
2,1Е10-04 |
1,475E-06 |
7,493E-10 |
6,641E-15 |
Таблиця 5.2 ─ Залежність імовірності помилки символу від параметрів коду 2
| q |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
| n |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
22 |
| k |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
12 |
| p |
0,188 |
0,128 |
0,074 |
0,033 |
9,86Е10-3 |
1,624E-03 |
1,062E-04 |
1,66E-06 |
| Pпд |
0,81 |
0,549 |
0,219 |
0,034 |
1,28Е10-3 |
6,451E-06 |
1,844E-09 |
7,05E-15 |
| Pд |
0,184 |
0,125 |
0,05 |
7,76Е10-3 |
2,91Е10-4 |
1,466E-06 |
4,191E-17 |
1,602E-15 |
Найкращим вважаємо код з мінімально можливим q
в
і найменшим при цьому значенні n
, при яких забезпечується заданий ЕВК, – це мінімізує складність кодека. Після вибору коду слід розраховуємо залежність, що характеризує завадостійкість в каналі зв'язку з коректуючим кодом. Для цього змінюємо 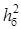 в таких межах, щоб величина р
д
приймала значення від 0,01 до значень, що дещо меншіза р
б
, будуємо залежності р
д1
=f
1
( в таких межах, щоб величина р
д
приймала значення від 0,01 до значень, що дещо меншіза р
б
, будуємо залежності р
д1
=f
1
(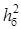 ) і р
д2
=f
2
( ) і р
д2
=f
2
(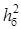 ) )

Рисунок 5.1 ─ Завадостійкість системи передачі з завадостійким кодуванням
Рис. 5.1 характеризує завадостійкість в каналі зв'язку з вибраним кодом. По цій залежності визначаємо необхідні відношення сигнал/шум на вході демодулятора 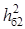 і і 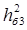 , при якому забезпечується допустима ймовірність помилки символу на виході декодера, тобто р
д
= р
б
. По знайдених значеннях , при якому забезпечується допустима ймовірність помилки символу на виході декодера, тобто р
д
= р
б
. По знайдених значеннях 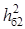 і і 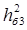 та одержаному при розрахунку завадостійкості демодулятора значенню та одержаному при розрахунку завадостійкості демодулятора значенню 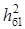 визначаємо ЕВК за формулою (5.1) і порівнюємо його з необхідним: визначаємо ЕВК за формулою (5.1) і порівнюємо його з необхідним:
D1
= 13,75 - 12,3 = 1,45 дБ D2
= 13,75 - 12,3 = 1,45 дБ
D < D1
; в < D2
.
Обидва коди забезпечують задане ЕВК.
6 РОЗРАХУНОК ЕФЕКТИВНОСТІ СИСТЕМ ЗВ'ЯЗКУ
Вихідні дані:
- тип каналу зв'язку – канал з постійними параметрами й адитивним білим гауссовим шумом;
- методи модуляції та параметри, що визначають ширину спектру модульованого сигналу: модуляція дискретна – тривалість біта Т
б
= 3,333∙10-3
с, число позицій сигналу М
= 128, швидкість коду1 k
/n=
0.782 ; швидкість коду2 k
/n=
0.545 ;
- відношення сигнал/шум на виході каналу зв'язку, при яких забезпечується задана якість відтворення повідомлення: при дискретній модуляції
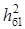 = 13,75 дБ , = 13,75 дБ , 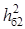 = 12,3 дБ , = 12,3 дБ , 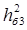 = 12,3 дБ; = 12,3 дБ;
- продуктивність джерела повідомлень R
д
= 300 біт/с.
Вимагається:
- розрахувати пропускну здатність каналу зв'язку С
для всіх розглянутих варіантів передачі та зіставити її значення з продуктивністю джерела повідомлень R
д
;
- розрахувати коефіцієнти інформаційної, частотної та енергетичної ефективності для всіх розглянутих варіантів передачі;
- побудувати графік межі Шеннона;
- порівняти ефективність розглянутих варіантів передачі між собою та з граничною ефективністю.
Розрахункові співвідношення та порядок розрахунку
При розрахунках ефективності під каналом зв'язку розуміють сукупність засобів, що забезпечують передачу сигналів від виходу модулятора до входу демодулятора.
Пропускна здатність неперервного каналу зв'язку визначається формулою Шеннона :
С = F log(1+Pc
/Pш
)
Смуга пропускання каналу зв'язку F
к
, що входить до цієї формули, приймається рівною ширині спектру модульованого сигналу Fs
.
При передачі сигналів дискретної модуляції мінімально можлива ширина спектру сигналів визначається межею Найквіста:
при ЧМ-M
Fs
= M
/(T
log2
M
),(6.1)
де Т
– тривалість двійкового символу на вході модулятора;
М
– число позицій сигналу.
Якщо в системі передачі відсутнє завадостійке кодування, то значення Т
дорівнює тривалості двійкового символу Т
б
на виході АЦП або кодера простого коду. Якщо ж використовується завадостійке кодування, то Т
= Т
б
k
/n
, де n
і k
- параметри корегуючого коду. Пропускну здатність неперервного каналу зв'язку розраховуємо для всіх розглянутих у курсовій роботі варіантів передачі. Зіставляємо отримані значення пропускної здатності каналу зв'язку С
з продуктивністю джерела R
д
, знайдену при розрахунку інформаційних характеристик джерела повідомлень.
Ефективність систем зв'язку оцінюють коефіцієнтами інформаційної, частотної та енергетичної ефективності, що визначаються формулами:
β = R/ρ0
; γ
= R/F; η = R/C; (6.4)
Ці формули визначають ефективність використання відповідно пропускної здатності каналу зв'язку С
, смуги пропускання каналу зв'язку F
к
і відношення сигнал/шум Р
s
/N
0
на виході каналу зв'язку при заданих методі передачі та якості відтворення повідомлення, що передається. Для розрахунків ефективності швидкість передачі інформації R
приймаємо рівною продуктивності джерела R
д
– при тій якості відтворення повідомлень, яка має місце в розраховуваній системі зв'язку, втратами інформації в каналі зв'язку можна знехтувати.
С
³R
д
Коефіцієнти ефективності розраховуємо для всіх варіантів передачі, результати розрахунків F
к
, Рs
/N
0
, С
, h,g і b подаємо у вигляді таблиці.
Таблиця 6.1 ─ Розрахунок коефіцієнтів ефективності системи передачі без кодування і з завадостійким кодуванням
| F
к
, Hz
|
Рs
/N
0
|
С,біт/с
|
10lg(
h)
|
10lg(
g)
|
10lg(
b)
|
ДС
без кодування
|
600 |
7,114E+3 |
1.019E+4 |
-14,081 |
-3,0103 |
-13,75 |
ДС1
з кодом1
|
766,627 |
6,48E+3 |
1.048E+4 |
-15.1 |
-4,074 |
-13,345 |
ДС2
з кодом2
|
1,1E+3 |
9,27E+3 |
9.870E+3 |
-16.842 |
-5,642 |
-14,902 |
R
д
= 300 біт/с.
С
³R
д
, отже існує спосіб кодування і декодування, при якому імовірність помилкового декодування може бути як завгодно мала.
Розраховуємо і будуємо графік граничної залежності b = f
(g) – межа Шеннона. Значення b і g відкладають у логарифмічних одиницях – відповідно 10lgb і 10lgg.
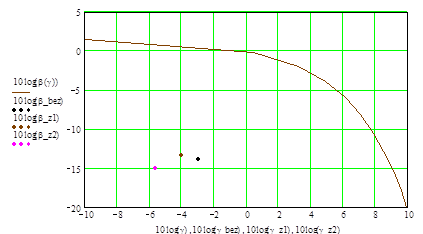
Рисунок 6.1 ─ Межа Шеннона
На рисунку 6.1 подаємо точками з координатами b
і g
всі розглянуті варіанти передачі. Порівнявши три варіанти передачі (без кодування, з кодом 1, та з кодом 2) ми дійшли до висновку, що найбільший виграш по енергетичній ефективності b
у системі передачі ,без коду, а по частотній ефективності g
─ у системі передачі з кодуванням один (ДС1). Найбільш доцільно використовувати код 2 у системі передачі, тому що у порівнянні з кодом 1 у нього більший енергетичний виграш b
і більша частотна ефективність g
. Щоб збільшити частотну і енергетичну ефективність необхідно збільшити продуктивність джерела повідомлень Rд
.
ЗАКЛЮЧЕННЯ ДО КУРСОВОЇ РОБОТИ
Дана курсова робота призначена для обчислення параметрів дискретного джерела повідомлень, а також можливої оптимізації. В першій частині курсової роботи ми побудували структурну схему такої системи передачі, а також намалювали осцилограми до кожного блоку. В наступних двох розділах ми порахували основні параметри джерела повідомлень, а саме ентропію, надлишковість, тривалість одного біта, кількість розрядів і тривалість одного символа. Як бачимо, коли ймовірності появи всіх символів однакові то надлишковість рівна нулю, що є ідеальною. Продуктивність джерела дорівнює 300 біт/с. При заданому виді модуляції і ймовірності появи помилки ми побудували залежність ймовірності появи помилки на виході декодера від відношення сигнал шум і знайшли, що це значення дорівнює 13,75 дБ. Параметри джерела можна покращити використовуючи завадостійкі коди, що виправляють певну кількість помилок і знижують необхідне значення відношення сигнал шум. Це зниження якраз і визначає ЕВК коду, за допомогою якого вибирають і порівнюють коди. При виборі коду необхідно користуватися наступними правилами: n має бути як найменше, а qв
таким щоб підходило для заданого каналу, тобто ймовірності появи помилки. Визначений нами ЕВК був більший заданого, що забезпечує необхідний нам енергетичний виграш кодування. Перед впровадженням у використання системи передачі обов’язково необхідно провести розрахунок її ефективності і зробити висновок про доцільність її використання. Для цього розраховуємо пропускну здатність каналу зв’язку і зіставляємо її з продуктивністю джерела повідомлень, щоб визначити за теоремою Шеннона чи взагалі можливо передати дану інформацію від джерела повідомлень через канал зв’язку і чи існує спосіб кодування і декодування при який імовірність помилкового декодування може бути як завгодно малою. Для досліджуваної системи передачі дана умова забезпечується, отже спосіб кодування і декодування існує. Розраховуємо коефіцієнти інформаційної, частотної та енергетичної ефективності для всіх розглянутих варіантів передачі. Побудувавши графік межі Шеннона і відмітивши точки по коефіцієнтах енергетичної і частотної ефективності порівнюємо між собою ефективність розглянутих варіантів передачі між собою та з граничною ефективністю. Отже, зробивши загальний висновок можемо сказати, що досліджувана система є ефективною для використання. З завадостійким кодуванням у системі забезпечується необхідне ЕВК, і енергетична і частотна ефективності не виходять за межу Шеннона, що вказує на те, що всі параметри розраховані правильно.
ПЕРЕЛІК ПОСИЛАНЬ
1. Теория передачи сигналов: Учебник для вузов / А.Г. Зюко и др. - М.: Радио и связь, 1986.
2. Панфилов И.П., Дырда В.Е.. Теория электрической связи: Учебник для техникумов. - М.: Радио и связь, 1991.
|