Задание 1
В таблице приведены поквартальные данные о кредитах от коммерческого банка на жилищное строительство за 4 года (16 кварталов).
| t |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| Y (t) |
43 |
54 |
64 |
41 |
45 |
58 |
71 |
43 |
49 |
62 |
74 |
45 |
54 |
66 |
79 |
48 |
Требуется:
1. Построить адаптивную мультипликативную модель Хольта-Уинтерса с учетом сезонного фактора, применив параметры сглаживания α1
= 0,3; α2
= 0,6; α3
= 0,3.
2. Оценить точность построенной модели с использованием средней ошибки аппроксимации;
3. Оценить адекватность построенной модели на основе исследования:
случайности остаточной компоненты по критерию пиков;
независимости уровней ряда остатков по d-критерию (в качестве критических использовать уровни d1
= 1,10 и d2
= 1,37) и по первому коэффициенту автокорреляции при критическом уровне значения r1
= 0,32;
нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.
4. Построить точечный прогноз на 4 шага вперед, т.е. на 1 год.
5. Отобразить на графиках фактические, расчетные и прогнозные данные.
Решение:
1.
Для оценки начальных значений а (0) и b (0) применим линейную модель к первым 8 значениям Y (t). Линейная модель имеет вид:

Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения по формулам:
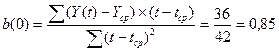

Таблица 1
| t |
Y (t) |
t-tср |
(t-tср) 2 |
Y-Yср |
(Y-Yср) х (t-tср) |
| 1 |
43 |
-4 |
12 |
-9 |
33 |
| 2 |
54 |
-3 |
6 |
2 |
-4 |
| 3 |
64 |
-2 |
2 |
12 |
-17 |
| 4 |
41 |
-1 |
0 |
-11 |
6 |
| 5 |
45 |
1 |
0 |
-7 |
-4 |
| 6 |
58 |
2 |
2 |
6 |
8 |
| 7 |
71 |
3 |
6 |
19 |
47 |
| 8 |
43 |
4 |
12 |
-9 |
-33 |
| 36
|
419
|
0
|
42
|
0
|
36
|
Произведем расчет:

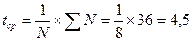
Получим линейное уравнение вида:

Для сопоставления фактических данных и рассчитанных по линейной модели значений составим таблицу.
Таблица 2. Сопоставление фактических и расчетных значений по линейной модели
| t |
Y (t) |
Yp
(t) |
| 1 |
43 |
49,42 |
| 2 |
54 |
50,26 |
| 3 |
64 |
51,11 |
| 4 |
41 |
51,95 |
| 5 |
45 |
52,80 |
| 6 |
58 |
53,64 |
| 7 |
71 |
54,49 |
| 8 |
43 |
55,33 |
Коэффициент сезонности есть отношение фактического значения экономического показателя к значению, рассчитанному по линейной модели.
Поэтому в качестве оценки коэффициента сезонности I квартала F (-3) может служить отношение фактических и расчетных значений Y (t) I квартала первого года, равное  , и такое же отношение для I квартала второго года (т.е. за V квартал t=5) , и такое же отношение для I квартала второго года (т.е. за V квартал t=5)  . .
Для окончательной, более точной, оценки этого коэффициента сезонности можно использовать среднее арифметическое значение этих двух величин.
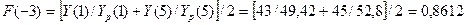
Аналогично находим оценки коэффициентов сезонности для II, III и IV кварталов:

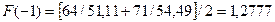
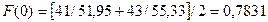
Построим адаптивную мультипликативную модель Хольта-Уинтерса (табл. 3) используя следующие формулы:
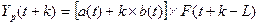

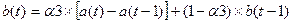

Таблица 3. Модель Хольта-Уинтерса
| t |
Y (t) |
a (t) |
b (t) |
F (t) |
Yp (t) |
Абс. погр.,
E (t)
|
Отн. погр.,
в%
|
| 0 |
48,57 |
0,85 |
0,8612 |
- |
- |
| 1 |
43 |
49,57 |
0,89 |
0,8650 |
42,56 |
0,44 |
1,03 |
| 2 |
54 |
50,35 |
0,86 |
1,0746 |
54,39 |
-0,39 |
0,72 |
| 3 |
64 |
50,88 |
0,76 |
1,2658 |
65,43 |
-1,43 |
2,24 |
| 4 |
41 |
51,85 |
0,82 |
0,7877 |
40,44 |
0,56 |
1,37 |
| 5 |
45 |
52,48 |
0,76 |
0,8605 |
45,56 |
-0,56 |
1,24 |
| 6 |
58 |
53,46 |
0,83 |
1,0807 |
57,21 |
0,79 |
1,36 |
| 7 |
71 |
54,83 |
0,99 |
1,2833 |
68,73 |
2,27 |
3, 20 |
| 8 |
43 |
55,45 |
0,88 |
0,7803 |
43,97 |
-0,97 |
2,26 |
| 9 |
49 |
56,52 |
0,94 |
0,8644 |
48,47 |
0,53 |
1,07 |
| 10 |
62 |
57,43 |
0,93 |
1,0801 |
62,09 |
-0,09 |
0,15 |
| 11 |
74 |
58,15 |
0,87 |
1,2769 |
74,89 |
-0,89 |
1, 20 |
| 12 |
45 |
58,61 |
0,74 |
0,7728 |
46,05 |
-1,05 |
2,34 |
| 13 |
54 |
60,29 |
1,03 |
0,8832 |
51,31 |
2,69 |
4,99 |
| 14 |
66 |
61,25 |
1,01 |
1,0785 |
66,23 |
-0,23 |
0,34 |
| 15 |
79 |
62,14 |
0,97 |
1,2735 |
79,50 |
-0,50 |
0,63 |
| 16 |
48 |
62,81 |
0,88 |
0,7676 |
48,77 |
-0,77 |
1,61 |
| 25,75 |
Проверка качества модели.
Для того чтобы модель была качественной уровни, остаточного ряда E (t) (разности  между фактическими и расчетными значениями экономического показателя) должны удовлетворять определенным условиям (точности и адекватности). Для проверки выполнения этих условий составим таблицу 4. между фактическими и расчетными значениями экономического показателя) должны удовлетворять определенным условиям (точности и адекватности). Для проверки выполнения этих условий составим таблицу 4.
Таблица 4. Промежуточные расчеты для оценки адекватности модели
| t |
E (t) |
Точка поворота |
E (t) 2
|
[E (t) - E (t-1)] 2
|
E (t) xE (t-1) |
| 1 |
0,44 |
- |
0, 194 |
- |
- |
| 2 |
-0,39 |
0 |
0,150 |
0,69 |
-0,17 |
| 3 |
-1,43 |
1 |
2,05 |
1,09 |
0,55 |
| 4 |
0,56 |
1 |
0,32 |
3,98 |
-0,81 |
| 5 |
-0,56 |
1 |
0,31 |
1,26 |
-0,32 |
| 6 |
0,79 |
0 |
0,62 |
1,81 |
-0,44 |
| 7 |
2,27 |
1 |
5,17 |
2,21 |
1,79 |
| 8 |
-0,97 |
1 |
0,95 |
10,54 |
-2,21 |
| 9 |
0,53 |
1 |
0,28 |
2,24 |
-0,51 |
| 10 |
-0,09 |
0 |
0,01 |
0,38 |
-0,05 |
| 11 |
-0,89 |
0 |
0,78 |
0,63 |
0,08 |
| 12 |
-1,05 |
1 |
1,11 |
0,03 |
0,93 |
| 13 |
2,69 |
1 |
7,26 |
14,03 |
-2,83 |
| 14 |
-0,23 |
0 |
0,05 |
8,52 |
-0,61 |
| 15 |
-0,50 |
0 |
0,25 |
0,07 |
0,11 |
| 16 |
-0,77 |
- |
0,60 |
0,08 |
0,38 |
| Сумма |
0,41 |
8,00 |
20,09 |
47,57 |
-4,09 |
2.
Проверка точности модели.
Будем считать, что условие точности выполнено, если относительная погрешность (абсолютное значение отклонения abs{E (t) }, поделенное на фактическое значение Y (t) и выраженное в процентах 100%* abs{E (t) }/ Y (t) в среднем не превышает 5%. Суммарное значение относительных погрешностей составляет 25,75. Средняя величина: 25,75/16=1,61%, значит, условие точности выполнено.
3.
Проверка условия адекватности.
Для того чтобы модель была адекватна исследуемому процессу, ряд остатков E (t) должен обладать свойствами случайности, независимости последовательных уровней, нормальности распределения.
Проверка случайности уровней.
Проверку случайности уровней остаточной компоненты (гр.2 табл.4) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда Е сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в гр.3 табл.4 для этой строки ставится 1, в противном случае в гр.3 ставится 0. В первой и в последней строке гр.3 табл.4 ставится прочерк или иной знак, так как у этого уровня нет двух соседних уровней. сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и в гр.3 табл.4 для этой строки ставится 1, в противном случае в гр.3 ставится 0. В первой и в последней строке гр.3 табл.4 ставится прочерк или иной знак, так как у этого уровня нет двух соседних уровней.
Общее число поворотных точек в нашем примере равно р=8.
Рассчитаем значение  : :

Функция int означает, что от полученного значения берется только целая часть. При N = 16.

Так как количество поворотных точек р= 8 больше q=6, то условие случайности уровней ряда остатков выполнено.
Проверка независимости уровней ряда остатков (отсутствия автокорреляции). Проверку проводим двумя методами:
1) по d-критерию критерий Дарбина-Уотсона (критические уровни d1
=1,10 и d2
=1,37):

Так как полученное значение больше 2, то величину в уточним:
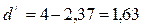
Условие выполнено (1,37<1,63<2), следовательно, уровни ряда Е (t) являются независимыми.
2) по первому коэффициенту автокорреляции r (1):

Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения  < rтабл.,
то уровни ряда остатков независимы. Для нашей задачи критический уровень rтабл.
= 0,32. Имеем: < rтабл.,
то уровни ряда остатков независимы. Для нашей задачи критический уровень rтабл.
= 0,32. Имеем:  =0,20 < rтабл.
= 0,32 - значит уровни независимы. =0,20 < rтабл.
= 0,32 - значит уровни независимы.
Проверка соответствия ряда остатков нормальному распределению определяем по
RS-критерию.
Рассчитаем значение RS:
 , ,
где  - максимальное значение уровней ряда остатков - максимальное значение уровней ряда остатков 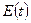 ; ;
 - минимальное значение уровней ряда остатков - минимальное значение уровней ряда остатков 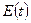  ; ;
S- среднее квадратическое отклонение.
Emax
- Emin
= 2,69 - (-1,43) = 4,13
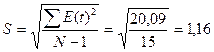
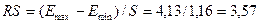
Уровни ряда остатков подчиняются нормальному распределению т.к полученное значение RS (3,57) попадает в заданный интервал (3,00<3,57<4,21).
Таким образом, все условия адекватности и точности выполнены. Следовательно, можно говорить об удовлетворительном качестве модели и возможности проведения прогноза показателя Yp
(t) на год.
4.
Расчет прогнозных значений экономического показателя.
Составим прогноз на четыре квартала вперед (т.е. на 1 год, с t=17 по t=20). Максимальное значение t, для которого могут быть рассчитаны коэффициенты  и и 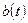 определяется количеством исходных данных и равно 16. Рассчитав значения определяется количеством исходных данных и равно 16. Рассчитав значения  и и  (см. табл.1.4) по формуле: (см. табл.1.4) по формуле:
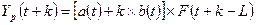 , ,
где k- период упреждения;
 - расчетное значение экономического показателя для t-го периода; - расчетное значение экономического показателя для t-го периода;
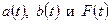 - коэффициенты модели; - коэффициенты модели;
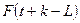 - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель; - значение коэффициента сезонности того периода, для которого рассчитывается экономический показатель;
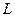 - период сезонности. - период сезонности.
Определим прогнозные значения экономического показателя Yp
(t) для: t = 17, 18,19 и 20.

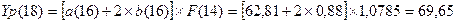


5.
На нижеприведенном рисунке проводится сопоставление фактических и расчетных данных. Здесь же показаны прогнозные значения о кредитах на год вперед. Из рисунка видно, что расчетные данные хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.
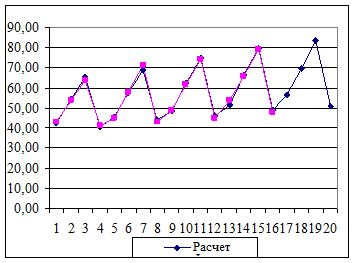
Рис.1. Сопоставление расчетных и фактических данных
Даны цены (открытия, максимальная, минимальная и закрытия) за 10 дней. Интервал сглаживания принять равным 5 дням.
| Дни |
Цены |
| макс. |
мин. |
закр. |
| 1 |
858 |
785 |
804 |
| 2 |
849 |
781 |
849 |
| 3 |
870 |
801 |
806 |
| 4 |
805 |
755 |
760 |
| 5 |
785 |
742 |
763 |
| 6 |
795 |
755 |
795 |
| 7 |
812 |
781 |
800 |
| 8 |
854 |
791 |
853 |
| 9 |
875 |
819 |
820 |
| 10 |
820 |
745 |
756 |
Рассчитать: экспоненциальную скользящую среднюю; момент; скорость изменения цен; индекс относительной силы; % R,% К,% D;
Расчеты проводить для всех дней, для которых эти расчеты можно выполнить на основании имеющихся данных.
Решение:
Для расчета экспоненциальной скользящей
средней воспользуемся формулой:
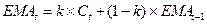 , ,
где k = 2/ (n + 1),
 -
цена закрытия t-го дня; -
цена закрытия t-го дня;
 - значение EMA текущего дня t. - значение EMA текущего дня t.
Момент
рассчитывается как разница конечной цены текущего дня  и цены n дней тому назад и цены n дней тому назад  : :

где  - цена закрытия t-го дня. - цена закрытия t-го дня.
 - значение МОМ текущего дня t. - значение МОМ текущего дня t.
Скорость изменения цен
рассчитываем как отношение конечной цены текущего дня к цене n дней тому назад, выраженное в процентах:
 , ,
где  - цена закрытия t-го дня. - цена закрытия t-го дня.
 - значение ROC текущего дня t. - значение ROC текущего дня t.
Таблица 1. Результаты расчетов экспоненциальной скользящей средней, момента, скорости изменения цен
| Дни |
Цены закр |
ЕМАt
|
МОМt
|
ROCt
|
| 1 |
804 |
804,00 |
- |
- |
| 2 |
849 |
819,00 |
- |
- |
| 3 |
806 |
814,67 |
- |
- |
| 4 |
760 |
796,44 |
- |
- |
| 5 |
763 |
785,30 |
- |
- |
| 6 |
795 |
788,53 |
-9,0 |
98,88 |
| 7 |
800 |
792,35 |
-49,0 |
94,23 |
| 8 |
853 |
812,57 |
47,0 |
105,83 |
| 9 |
820 |
815,05 |
60,0 |
107,89 |
| 10 |
756 |
795,36 |
-7,0 |
99,08 |
Для расчета индекса относительной силы
используем формулу:
 , ,
где AU- сумма приростов конечных цен за n последних дней;
AD- сумма убыли конечных цен за n последних дней.
Таблица 2. Результаты расчета индекса относительной силы
| Дни |
Цены закрытия |
Изменение (+/-) |
RSI |
| 1 |
804 |
45 |
- |
| 2 |
849 |
-43 |
- |
| 3 |
806 |
-46 |
- |
| 4 |
760 |
3 |
- |
| 5 |
763 |
32 |
- |
| 6 |
795 |
5 |
47,3 |
| 7 |
800 |
53 |
31,0 |
| 8 |
853 |
-33 |
66,9 |
| 9 |
820 |
-64 |
73,8 |
| 10 |
756 |
45 |
48,1 |
Рассчитаем %R, %К, %D используя следующие формулы:
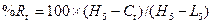 , ,
где  - значение индекса текущего дня t; - значение индекса текущего дня t;
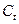 -
цена закрытия t-го дня; -
цена закрытия t-го дня;
L5
и Н5
- минимальная и максимальные цены за n предшествующих дней, включая текущие.
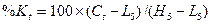 , ,
где 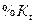 - значение индекса текущего дня t; - значение индекса текущего дня t;
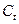 -
цена закрытия t-го дня; -
цена закрытия t-го дня;
L5
и Н5
- минимальная и максимальная цены за 5 предшествующих дней, включая текущие.
Индекс % в рассчитывается аналогично индексу %К, с той лишь разницей, что при его построении величины  и и  сглаживают, беря их трехдневную сумму. сглаживают, беря их трехдневную сумму.
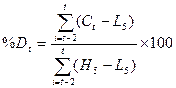
Таблица 3. Результаты расчетов %R, %К, %D
| Дни |
Цены |
% Kt
|
% Rt
|
%Dt
|
| макс |
мин |
закр |
| 1 |
858 |
785 |
804 |
- |
- |
| 2 |
849 |
781 |
849 |
- |
- |
- |
| 3 |
870 |
801 |
806 |
- |
- |
- |
| 4 |
805 |
755 |
760 |
- |
- |
- |
| 5 |
785 |
742 |
763 |
16,41 |
83,59 |
- |
| 6 |
795 |
755 |
795 |
41,41 |
58,59 |
- |
| 7 |
812 |
781 |
800 |
45,31 |
54,69 |
34,38 |
| 8 |
854 |
791 |
853 |
99,11 |
0,89 |
60,33 |
| 9 |
875 |
819 |
820 |
58,65 |
41,35 |
66,22 |
| 10 |
820 |
745 |
756 |
8,46 |
91,54 |
53,33 |
3.1
Банк выдал ссуду, размером 5 000 000 руб. Дата выдачи ссуды 08.01.02, возврата 22.03.02. День выдачи и день возврата считать за 1 день. Проценты рассчитываются по простой процентной ставке 55% годовых. Найти:
3.1 1) точные проценты с точным числом дней ссуды;
3.1 2) обыкновенные проценты с точным числом дней ссуды;
3.1 3) обыкновенные проценты с приближенным числом дней ссуды.
Решение:
3.1 1) К = 365, t = 73, I = 5 000 000 х 0,55 х 73/365 = 550 000,00 руб.
3.1 2) К = 360, t = 73, I = 5 000 000 х 0,55 х 73/360 = 557 638,89 руб.
3.1 3) К = 360, t = 74, I = 5 000 000 х 0,55 х 74/360 = 565 277,78 руб.
3.2
Через 90 дней после подписания договора должник уплатил 5 000 000 руб.
Кредит выдан под 55% годовых (проценты обыкновенные).
Какова первоначальная сумма и дисконт?
Решение:
P = S / (1 + ni) = 5 000 000/ (1 + 0,55 х 90/360) = 4 395 604,40 руб.
D = S- P = 5 000 000 - 3 395 604,40 = 604 395,60руб.
3.3
Через 90 предприятие должно получить по векселю 5 000 000 руб. Банк приобрел этот вексель с дисконтом. Банк учел вексель по учетной ставке 55% годовых (год равен 360 дням). Определить полученную предприятием сумму и дисконт.
Решение:
D = Snd
= 5 000 000 x 0,55 х 90/360 = 687 500,00 руб.
P = S- в = 5 000 000 - 687 500,00= 4 312 500,00 руб.
3.4
В кредитном договоре на сумму 5 000 000 руб. и сроком на 5 лет, зафиксирована ставка сложных процентов, равная 55% годовых. Определить наращенную сумму.
Решение:
S = Px (1+i) n
= 5 000 000 х (1+0,55) 5
= 44 733 048,44 руб.
3.5
Сумма размером 5 000 000 руб. представлена на 5 лет. Проценты сложные, ставка 55% годовых. Проценты начисляются 4 раза в году. Вычислить наращенную сумму.
Решение:
N = 5 x 4 = 20
S = Px (1+j / m) N
= 5 000 000 х (1 + 0,55/4) 20
= 65 765 497,67 руб.
3.6.
Вычислить эффективную ставку процентов, если банк начисляет проценты 4 раза в год, исходя из номинальной ставки 55% годовых.
Решение:
iэ
= (1 + j / m) m -
1 = (1 + 0,55/4) 4
- 1 = 0,6742, т.е.67,42%.
3.7.
Определить, какой должна быть номинальная ставка при начислении процентов 4 раза в году, чтобы обеспечить эффективную ставку 55% годовых.
Решение:
j = mx [ (1 + iэ
) 1/
m
- 1] = 4 x [ (1 + 0,55) (1/4)
- 1] = 0,46316, т.е.46,316%.
3.8.
Через 5 лет предприятию будет выплачена сумма 5 000 000 руб. Определить ее современную стоимость при условии, что применяется сложная процентная ставка 55% годовых.
Решение:
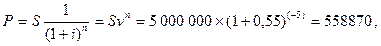 руб. руб.
3.9.
Через 5 лет по векселю должна быть выплачена сумма 5 000 000 руб. Банк учел вексель по учетной ставке 55% годовых. Определить дисконт.
Решение:
P = S (1 - dсл
) n
= 5 000 000 x (1 - 0,55) 5
= 92 264,06 руб.
D = S- P = 5 000 000 - 92 264,06 = 4 907 735,94 руб.
3.10.
В течение 5 лет на расчетный счет в конце каждого года поступает по 5 000 000 руб., на которые 4 раза в году начисляются проценты по сложной годовой ставке 55%. Определить сумму на расчетном счете к концу указанного срока.
Решение:
 руб. руб.
|