Задачи на наибольшее и наименьшее значения функции
- Требуется изготовить коническую воронку с образующей l=10см. Каков должен быть радиус основания воронки, чтобы ее объем был наибольшим?
- Требуется изготовить закрытый цилиндрический бак емкостью V. При каком радиусе основания на изготовление бака уйдет наименьшее количество материала?
- Требуется изготовить открытый цилиндрический бак емкостью V. При каком радиусе основания на изготовление бака уйдет наименьшее количество материала?
- Проволоку длины l согнули так, что получился круговой сектор максимальной площади. Найдите центральный угол сектора.
- Найдите отношение высоты к радиусу основания цилиндра наибольшего объема, вписанного в данный конус. Высота конуса = H, радиус основания – R.
- Требуется изготовить коническую воронку с образующей l=15 см. Какова должна быть высота воронки, чтобы ее объем был наибольшим?
- Из всех прямоугольников с площадью 9 дм2
найдите тот, у которого периметр наименьший.
- Из всех прямоугольников с диагональю 4 дм найдите тот, у которого площадь наибольшая.
- Какой из прямоугольников периметром 80 см имеет наибольшую площадь? Вычислите площадь этого прямоугольника.
- В полушар радиуса 3 вписан конус так, что вершина конуса лежит в центре полушара. При каком радиусе основания этот конус будет иметь максимальный объем?
- В полушар радиуса 4 вписан цилиндр так, что плоскость основания цилиндра совпадает с плоскостью, ограничивающей полушар. Чему должна быть равна высота цилиндра, чтобы этот цилиндр имел наибольший объем?
- Найдите отношение высоты к радиусу основания цилиндра, который при заданном объеме имеет наименьшую полную поверхность.
- Найдите отношение высоты к радиусу основания конуса, который при заданном объеме имеет наименьшую боковую поверхность.
- Картина высоты 1,5 м повешена на стену так, что ее нижний край на 1,2 м выше глаза наблюдателя. На каком расстоянии от стены должен стать наблюдатель, чтобы его положение было наиболее благоприятно для осмотра картины (т.е. чтобы угол зрения был наибольшим)?
- Требуется изготовить ящик с крышкой, объем которого был бы равен V, причем стороны основания относились бы как 2:3. Каковы должны быть размеры всех сторон, чтобы полная поверхность была наименьшей?
Вычислить площадь фигуры, ограниченной линиями (сделав рисунок)
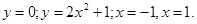 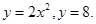  - дугой синусоиды
 на [0; p] и осью абсцисс. на [0; p] и осью абсцисс.
 - дугой синусоиды
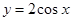 на [ на [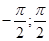 ] и осью абсцисс. ] и осью абсцисс.
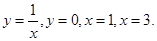  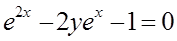 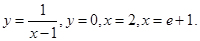 - осью Ох и кривой

 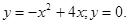   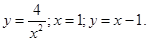 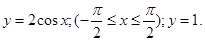 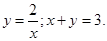 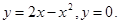   и осью Ох. и осью Ох.
Вычислить площадь фигуры, ограниченной линиями
1. 
2. 
3. 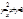
4. 
5. 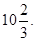
6. 
7. 
8. 
9. 
10.
11.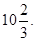
12.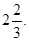
13.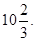
14.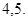
15.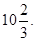
16.
17.
18.
19.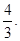
20.
21.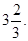
|