Министерство образования Российской Федерации
Южно-Уральский Государственный университет
Кафедра «Автомобильный транспорт»
Курсовая работа
на тему:
Рабочие процессы и элементы расчета механизмов автомобиля
Ford Fiesta
Выполнил:
Группа:
Проверил:
Челябинск
2008
АННОТАЦИЯ
СОДЕРЖАНИЕ
Введение. 4
1 Расчёт сцепления.. 5
2 РАСЧЕТ КОРОБКи ПЕРЕДАЧ. 9
3 Расчет карданной передачи.. 13
4 Расчет главной передачи.. 18
5 Расчет полуоси.. 23
6 Расчет рессоры.. 26
7 Расчет амортизатора.. 30
8 Расчет пружины.. 34
9 Расчет рулевого управления.. 36
10 Расчет тормозного управления.. 39
11 Расчет несущей части автомобиля.. 43
Литература.. 46
Введение
В результате интенсивного совершенствования конструкции автомобилей, более частого обновления выпускаемых моделей, придания им высоких потребительских качеств, отвечающих современным требованиям, возникает необходимость повышения уровня подготовки кадров в сфере Автомобильного транспорта.
Будущий инженер должен иметь представления о современном состоянии и тенденциях развития как автомобилестроения в целом, так и отдельных конструкций автомобилей, уметь оценивать эксплуатационные свойства на основе анализа конструкций моделей автомобилей, определять нагруженность отдельных элементов, чтобы прогнозировать их надежность, а также проводить испытания автомобилей и оценивать их результаты.
Задача раздела «Анализ конструкций и элементы расчета»- дать знания и навыки по анализу и оценке конструкций различных автомобилей и их механизмов, а также по определению нагрузок.
«Анализ конструкций, элементы расчета» подчинено общему принципу: анализ и оценка конструкций дается на базе предъявляемых требований и классификационных признаков, чему соответствует изучение рабочих процессов.
1 Расчёт сцепления
Сцепление – это механизм трансмиссии, передающий крутящий момент двигателя и позволяющий кратковременно отсоединять двигатель от трансмиссии и вновь их плавно соединять.
1.1
Алгоритм расчета сцепления
1. Расчетный момент сцепления Мс
двигателя:
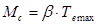 (1.1) (1.1)
2. Диаметр ведомого диска:
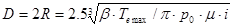 (1.2) (1.2)
где p0
=0.2МПа;
m=0.3;
I=2.
3. Внутренний радиус фрикционного кольца .
r= (0.6)R=0.075 м. (1.3)
4. Сумарная сила действующая на ведомый диск.
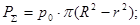 (1.4) (1.4)
4. Удельная работа буксования:
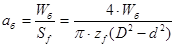 (1.5) (1.5)
где Wб – работа буксования определяется из зависимости: 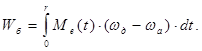 , ,
где ωд и ωа – угловые скорости соответственно ведущих и ведомых дисков,
Мс(t)- момент трения сцепления.
5. Расчет ведущего диска на нагрев:
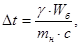 (1.6) (1.6)
где m н – масса диска,
с- удельная массовая теплоемкость.
6. Нажимное усилие одной витой пружины:
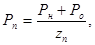 (1.7) (1.7)
где Р0 – суммарное усилие оттяжных и отжимных пружин сцепления, Р0 = (0,15-0,25)МПа,
zн – число нажимных пружин.
7. Жесткость пружины:
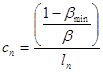 , (1.8) , (1.8)
где lн – величина износа накладок.
1.2 Обоснование выбора исходных данных для расчёта сцепления
1. р0
принимаем равным 0.2 Мпа так как автомобиль Ford Fiesta является легковым и предназначен для города.
2. Максимальный крутящий момент двигателя, Н*м: 204 Н·м [1, данные производителя].
3. Давление между поверхностями трения, кН/м^2: 25 [2, стр.148, таб.6.4], [3].
4. Коэффициент запаса сцепления: 1,8 на основании с ГОСТ 17786-80, для сцепления с ткаными фрикционными накладками [3, стр.63].
5. Число пар трения: 2 (I=2*n=2*1=2, где n=1 число ведущих дисков) [4, стр.50].
6. Число нажимных пружин: 10, взято из среднего значения числа возможного, так как Ford Fiesta относится к машинам небольшой массы [2, стр. 147].
7. Полный вес автомобиля, Н: 16150Н, [1, данные производителя].
8. Расчетный коэффициент трения при проектировании сцепления: 0,3 [3, стр. 63].
9. Передаточное число трансмиссии: 30,56 [1, данные производителя],
(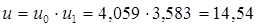 , где , где 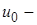 передаточное число главной передачи; передаточное число главной передачи; 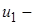 передаточное число первой передачи; передаточное число первой передачи;
10. Полный вес прицепа, Н: 5500 Н [1, данные производителя].
11. Радиус колеса, м: 0,33 м [1, данные производителя].
12. КПД трансмиссии: 0,92 [2, стр. 34].
13. Коэффициент дорожного сопротивления: 0,16 [5].
14. Коэффициент учета моментов инерции колес: 1,06 [5].
15. Масса ведущего диска, кг: 10, так как масса сцепления 12кг минус масса ведомого диска 2кг (по аналогии с ВАЗ-2109) [2, таблица 6.4 стр. 148].
16. Удельная массовая теплоемкость чугуна (стали), Дж/(кг*град): 481,5 (2, стр. 149).
17. Долю теплоты, приходящуюся на рассчитываемую деталь, принимают = 0.5 [3, стр. 53].
20. Допустимая величина износа накладок, м: 0,003м [2, стр. 144].
24. Число ведущих дисков: 1 [2, таблица 6.4 стр. 148].
1.3 Проведение расчета
Таблица 1 – Исходные данные для расчёта сцепления
| Угловая скорость коленвала при максимальном моменте, об/мин |
2600 |
| Максимальный крутящий момент двигателя, Н*м |
106 |
| Давление между поверхностями трения, кН/м^2 |
25 |
| Коэффициент запаса сцепления |
1,65 |
| Число пар трения |
2 |
| Число нажимных пружин |
10 |
| Полный вес автомобиля, Н |
16500 |
| Расчетный коэффициент трения |
0,3 |
| Передаточное число трансмиссии |
14,54 |
| Полный вес прицепа, Н |
5500 |
| Радиус колеса, м |
0,33 |
| КПД трансмиссии |
0,92 |
| Коэффициент дорожного сопротивления |
0,16 |
| Коэффициент учета моментов инерции колес |
1,06 |
| Масса ведущего диска, кг |
10 |
| Удельная массовая теплоемкость чугуна (стали), Дж/(кг*град) |
481,5 |
| Доля теплоты, приходящейся на рассчитываемую деталь |
0,5 |
Таблица 2 – Результаты расчета сцепления
| Нажимное усилие прижимных пружин, Н |
6836 |
| Наружный диаметр ведомого диска, м |
0,19 |
| Внутренний диаметр ведомого диска, м |
0,13 |
| Средний радиус, м |
0,16 |
| Сила сжатия фрикционных дисков сцепления, Н |
1643,7 |
| Нажимное усилие одной пружины, Н/м^2 |
683,6 |
| Работа буксования, кДж |
3049 |
| Перепад температур, град |
1,8624 |
| Максимальная сила, действующая на нажимную пружину, кН |
13,68 |
Коробка передач является агрегатом трансмиссии, преобразующим крутящий момент и частоту вращения по величине и направлению. Предназначена для получения различных тяговых усилий на ведущих колесах при троганнии автомобиля с места и его разгоне, при движении автомобиля и преодолении дорожных препятствий.
2.1
Алгоритм расчета КПП
1. Определение межосевого расстояния:
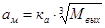 , (2.1) , (2.1)
где Ка = 8,6…9,3 – коэффициент для грузовых автомобилей и автобусов.
Мвых – крутящий момент на ведомом валу.
2. Диаметр ведущего вала в шлицевой части:
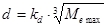 (2.2) (2.2)
где Kd – эмпирический коэффициент,
Мemax – максимальный крутящий момент двигателя.
3. Угол наклона β, удовлетворяющий условию εβ
= 1, определяют из равенства:
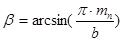 , (2.3) , (2.3)
где mn
– нормальный модуль.
4. Найдем уточненное значение угла наклона:
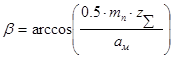 , (2.4) , (2.4)
где zΣ
– суммарное число зубьев.
5. Число зубьев зубчатых колес:
Zbщ
+ Zвм
= ZΣ
(2.5)
Zвм
/ Zвщ
= up
(2.6)
где Zbщ
– число зубьев ведущего зубчатого колеса
Zвм
число зубьев ведомого зубчатого колеса,
ZΣ
– суммарное число зубьев,
up
– передаточное число от ведущего зубчатого колеса к ведомому.
6. Необходимый момент трения синхронизатора:
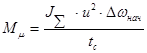 , (2.7) , (2.7)
где JΣ
– суммарный приведенный момент инерции для той части системы, угловая скорость которой изменяется под действием момента 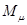 . .
U – передаточное число от вала, к которому приводится момент инерции, к включенному зубчатому колесу.
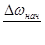 - начальная разность угловых скоростей вала и установленного на нем включенного зубчатого колеса. - начальная разность угловых скоростей вала и установленного на нем включенного зубчатого колеса.
7. Время синхронизации:
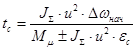 , (2.8) , (2.8)
где εс
– угловое замедление вала, на котором расположен синхронизатор.
2.2 Обоснование выбора исходных данных
1.Количество ступеней коробки передач 5, (1, данные производителя).
2.Максимальный крутящий момент на выходном валу, Нм: Mкр max = Mкр* U1*Uo = 106*3,58*4,06= 1540,7.
3. Радиус качения колеса автомобиля, м:0,33 (1, данные производителя).
4.Передаточные отношения главной передачи: 4,06 (1, данные производителя).
5.Угол наклона зубьев зубчатых колёс, град: т.к. прототип ВАЗ 2101 по М=106 Нм, то β=27 град, (2, стр.180, табл. 7.3).
6.Относительный пробег на 1, 2, 3, 4, 5 передачах составляет соответственно 0,01, 0,04, 0,2, 0,75, 0,75; [3].
7.Модули зубчатого зацепления 1,2,3,4,5 передач соответственно равны
4,25; 3,5; 3,5; 3,5; 3,5; (2, стр. 180, табл. 7.3).
8.Число зубьев ведущих шестерён 1, 2, 3, 4, 5 передач: 14, 25, 34, 43, 52, (2, стр.180, табл. 7.3).
9. Передаточное отношение передач 1, 2, 3, 4, 5: 3,67; 2,10; 1,36; 1,00; 0,82; (1, данные производителя).
2.3 Проведение расчета
Таблица 3- Исходные данные КПП
| Количество ступеней коробки передач |
5 |
| Максимальный крутящий момент на выходном валу, Н*м |
1631,7 |
| Радиус качения колеса автомобиля, м |
0,33 |
| Передаточное отношение главной передачи |
3,9 |
| Угол наклона зубьев зубчатых колёс, град |
22 |
| Относительный пробег на 1 передаче |
0,01 |
| Относительный пробег на 2 передаче |
0,04 |
| Относительный пробег на 3 передаче |
0,2 |
| Относительный пробег на 4 передаче |
0,75 |
| Относительный пробег на 5 передаче |
0,75 |
| Модуль зубчатого зацепления 1 передачи, мм |
4,25 |
| Модуль зубчатого зацепления 2 передачи, мм |
3,5 |
| Модуль зубчатого зацепления 3 передачи, мм |
3,5 |
| Модуль зубчатого зацепления 4 передачи, мм |
3,5 |
| Модуль зубчатого зацепления 5 передачи, мм |
3,5 |
| Число зубьев ведущей шестерни 1 передачи |
14 |
| Число зубьев ведущей шестерни 2 передачи |
25 |
| Число зубьев ведущей шестерни 3 передачи |
34 |
| Число зубьев ведущей шестерни 4 передачи |
43 |
| Число зубьев ведущей шестерни 5 передачи |
52 |
| Передаточное отношение 1 передачи |
3,67 |
| Передаточное отношение 2 передачи |
2,1 |
| Передаточное отношение 3 передачи |
1,36 |
| Передаточное отношение 4 передачи |
1,00 |
| Передаточное отношение 5 передачи |
0,82 |
Таблица 4- Результаты расчета КПП
| Межосевое расстояние, мм |
106 |
| Рабочая ширина венцов зубчатых колёс, мм |
22 |
| Ширина подшипников, мм |
24 |
| Осевой размер зубчатой муфты и синхронизатора, мм |
78 |
| Осевой размер картера коробки передач, мм |
296 |
| Диаметр ведомого вала (в средней части), мм |
60 |
| Диаметр промежуточного вала (в средней части), мм |
51 |
| Диаметр ведущего вала в шлицевой части, мм |
51 |
| Контактное напряжение зубьев 1 передачи, МПа |
76,02 |
| Контактное напряжение зубьев 2 передачи, МПа |
40,78 |
| Контактное напряжение зубьев 3 передачи, МПа |
25,92 |
| Контактное напряжение зубьев 4 передачи, МПа |
18,67 |
| Контактное напряжение зубьев 5 передачи, МПа |
| Напряжение изгиба зубьев 1 передачи, МПа |
146,1 |
| Напряжение изгиба зубьев 2 передачи, МПа |
67,55 |
| Напряжение изгиба зубьев 3 передачи, МПа |
36,52 |
| Напряжение изгиба зубьев 4 передачи, МПа |
22,83 |
| Напряжение изгиба зубьев 5 передачи, МПа |
| Ресурс коробки передач по контактным напряжениям, тыс.км |
115,6 |
| Ресурс коробки передач по усталостным напряжениям, тыс.км |
139,3 |
3 Расчет карданной передачи
Карданная передача автомобиля – это механизм трансмиссии, состоящий из одного или нескольких карданных валов и карданных шарниров, предназначенный для передачи крутящего момента между агрегатами, оси валов которых не совпадают или могут изменять свое относительное положение.
3.1
Алгоритм расчета карданной передачи
1. Критическая частота вращения карданного вала:
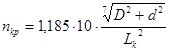 , ,
где в и в – соответственно наружный и внутренний диаметры карданного вала.
Lк – длина карданного вала.
2. Максимальная частота вращения карданного вала:
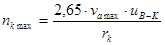 , ,
где Uв-к – передаточное число от карданного вала к ведущим колесам.
Vamax – максимальная скорость движения автомобиля.
3. Расчетный крутящий момент на карданном валу на низшей передаче в коробке передач:
M=M1
·U1
,
где M1
– крутящий момент на ведущем валу коробки передач, для механических трансмиссий.
U1
– передаточное число.
4. Определение допустимой длины карданного вала:
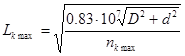 , ,
5. Напряжение кручения сплошного вала:
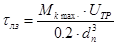 , ,
Мкmax – максимальный крутящий момент.
Uтр – передаточное число трансмиссии на первой передаче.
6. Угол закручивания карданного вала:
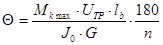 , ,
где Jo – момент инерции сечения вала трубчатого: 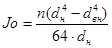 , ,
сплошного: 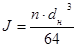
G – модуль упругости второго рода.
3.2 Обоснование выбора исходных данных
Рассчитаем высоту зубьев шлицев, средний радиус поверхности контакта зубьев, плечо условно сосредоточенной силы, действующей в середине шипа, момент сопротивления сечения шипа, диаметр отверстия в шипе крестовины для смазывания, силу, действующую на подшипник при расчетном моменте .
Высота зубьев шлицев:
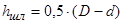 , ,
где в - наружный диаметр шлицев, D=45;
d - внутренний диаметр шлицев, d=40,6
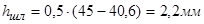 . .
Средний радиус поверхности контакта зубьев:
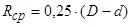 ; ;
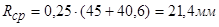 . .
Плечо условно сосредоточенной силы, действующей в середине шипа:
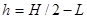 , ,
где H - размер между торцами крестовины, H=57,17 мм;
L-для иглы, L=10 мм .
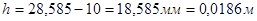 . .
Момент сопротивления сечения шипа:
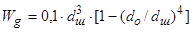 , ,
где dш
- диаметр шипа, dш
=0,0141 м;
do
- диаметр отверстия для смазывания;
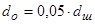 ; ;
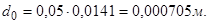
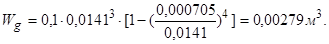
Сила Pp
, действующая на подшипник при расчетном моменте:
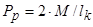 , ,
где lk
-расстояние между серединами игольчатых роликов противоположных карданных подшипников, lk
-=0,04717 м;
M-расчетный крутящий момент на карданном валу:
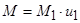 , ,
 Н м; Н м;
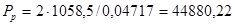 Н. Н.
Момент сопротивления кручения трубы карданного вала, коэффициент динамичности, полярный момент инерции сечения, модуль упругости при кручении, длина шлицев, коэффициент, учитывающий неравномерное распределение нагрузки по зубьям, плечо "А" опасного сечения в вилке карданного шарнира, момент сопротивления изгибу опасного сечения вилки шарнира, плечо "С" опасного сечения в вилке карданного шарнира, момент сопротивления кручения опасного сечения вилки карданного шарнира, коэффициент прогиба, поправочный коэффициент, учитывающий угол установки карданного вала выбраны согласно рекомендациям в [3].
Наружный диаметр сечения вала, внутренний диаметр сечения вала, расстояние между центрами карданов, передаточное число от карданного вала к ведущим колесам, длина трубы карданного вала, расстояние между серединами игольчатых роликов, угол установки карданного вала, число игл подшипника, диаметр иглы подшипника, длина иглы подшипника, частота вращения карданного вала при средней скорости движения автомобиля выбраны согласно рекомендациям в [2].
Максимальная скорость движения автомобиля, радиус качения колеса, крутящий момент на ведущем валу коробки передач, передаточное число коробки передач выбраны согласно данным в [1].
3.3 Проведение расчета
Таблица 7 - Исходные данные для расчета карданной передачи
| Наружный диаметр сечения вала, мм |
70 |
| Внутренний диаметр сечения вала, мм |
66 |
| Расстояние между центрами карданов, мм |
785 |
| Максимальная скорость движения автомобиля, км/ч |
135 |
| Передаточное число от карданного вала к ведущим колёсам |
3.9 |
| Радиус качения колеса, м |
0,33 |
| Крутящий момент на ведущем валу коробки передач, Н*м |
114 |
| Передаточное число коробки передач на низшей передаче |
3,67 |
| Момент сопротивления кручения трубы карданного вала, мм^3 |
0,0141 |
| Коэффициент динамичности |
3 |
| Длина трубы карданного вала, м |
0,765 |
| Полярный момент инерции сечения, мм^4 |
0,0048 |
| Модуль упругости при кручении, МПа |
85000 |
| Число шлицев |
17 |
| Высота зубьев шлицев, м |
0,0022 |
| Длина шлицев, м |
0,06 |
| Средний радиус поверхности контактов зубьев, м |
0,0214 |
| Коэф-т, учитывающий неравномерное распределение нагрузки по зубьям |
0,75 |
| Расстояние между серединами игольчатых роликов, мм |
47,17 |
| Угол установки карданного вала, град |
2 |
| Плечо условно сосредоточенной силы, действующей в середине шипа, м |
0,0186 |
| Момент сопротивления сечения шипа, мм^3 |
0,012 |
| Диаметр шипа крестовины, м |
0,0141 |
| Диаметр отверстия в шипе крестовины для смазывания, м |
0,000705 |
| Плечо "А" опасного сечения в вилке карданного шарнира, м |
0,005 |
| Момент сопротивления изгибу опасного сечения вилки шарнира, мм^3 |
0,008 |
| Плечо "C" опасного сечения в вилке карданного шарнира, м |
0,0023 |
| Момент сопротивления кручению опасного сечения вилки шарнира, мм^3 |
0,008 |
| Число игл подшипника |
22 |
| Диаметр иглы подшипника, мм |
2,4 |
| Длина иглы подшипника, мм |
10 |
| Частота вращения кард. вала при средней скорости движения а/м, об/мин |
2600 |
| Коэффициент прогиба |
1,1 |
| Сила действующая на подшипник при расчётном моменте, Н |
23523 |
| Поправочный коэф-т, учитывающий угол установки карданного вала |
4 |
Таблица 8 - Результаты расчета карданной передачи
| Критическая частота вращения коленчатого вала, об/мин |
1561 |
| Максимальная частота вращения коленчатого вала, об/мин |
4228 |
| Допустимая длина коленчатого вала, мм |
452,5 |
| Расчётный крутящий момент на карданном валу на низшей передаче, Н*м |
418,4 |
| Напряжение кручения трубы под действием расчётного момента, Па |
2,97E+04 |
| Максимальный динамический момент, Н*м |
1255 |
| Напряжения кручения трубы под действием динамического момента, Па |
8,90E+04 |
| Угол закручивания трубы карданного вала, град |
1,35E+04 |
| Напряжение смятия боковых поверхностей шлицев, Па |
11,62 |
| Условно сосредоточенная нормальная сила, действующая в середине шипа, Н |
8875 |
| Напряжение изгиба шипа крестовины в опасном сечении, Па |
1,38E+04 |
| Напряжение среза шипа крестовины в опасном сечении, МПа |
57,01 |
| Напряжение изгиба в опасном сечении вилки шарнира, Па |
5547 |
| Напряжение среза в опасном сечении вилки шарнира, Па |
2552 |
| Динамическая грузоподъёмность подшипника, кН |
6,134 |
| Пробег автомобиля до выхода подшипника из строя, тыс.км |
158,5 |
Обратившись к [2] можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям и данная карданная передача годна к эксплуатации.
4 Расчет главной передачи
Главная передача – механизм трансмиссии автомобиля, преобразующий крутящий момент и расположенный перед ведущими колесами автомобиля.
4.1 Алгоритм расчета главной передачи
a. Радиус средней точки зуба ведущей шестерни:
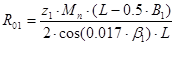
2. Радиус средней точки зуба ведомой шестерни:
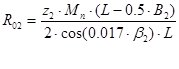 , ,
где Z1 – число зубьев ведущей шестерни;
Z2 - число зубьев ведомой шестерни;
L – длина образующей делительного конуса;
В1 – длина зубьев ведущей шестерни;
В – длина зубьев ведомой шестерни;
β1 – угол наклона винтовой линии;
Mn – расчетное значение величины нормального зацепления;
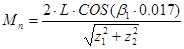
3. Половина угла при вершине начального конуса ведущей шестерни:
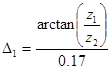
3. Половина угла при вершине начального конуса ведомой шестерни
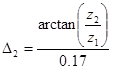
4. Радиус кривизны зуба ведущей шестерни:
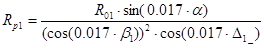
5. Радиус кривизны зуба ведомой шестерни:
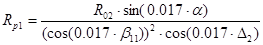
6. Эквивалентное число зубьев ведущей шестерни:
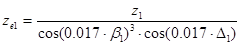
7. Эквивалентное число зубьев ведомой шестерни:
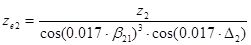 . .
8. Торцевой шаг по основанию конуса ведущей шестерни:
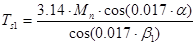
9. Торцевой шаг по основанию конуса ведомой шестерни:
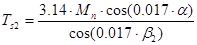
10. Окружная сила ведущей шестерни:
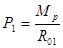
11. Окружная сила ведомой шестерни:
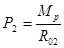 , ,
где Мр – расчетный крутящий момент.
12. Осевая сила шестерни (i = 1 – ведущей, i = 2 – ведомой):

13.Радиальная сила шестерни (i = 1 – ведущей, i = 2 – ведомой):
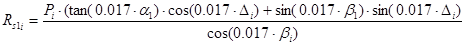
14.Напряжение изгиба (i = 1 – ведущей, i = 2 – ведомой):
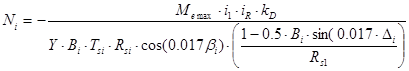
где i1
– передаточное число 1 – й передачи;
iR
– передаточное число раздаточной коробки;
kD
– коэффициент динамичности;
Y – коэффициент формы зуба.
15.Напряжение смятия шестерни (i = 1 – ведущей, i = 2 – ведомой):
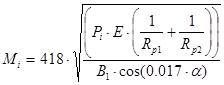
16.Ресурс главной передачи:
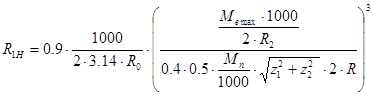 , ,
где Rо – радиус качения колеса.
R2 – расчетное значение радиуса начальной окружности ведомой шестерни:
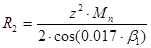
4.2 Обоснование выбора исходных данных
Рассчитаем длину зубьев ведущей шестерни, длину зубьев ведомой шестерни.
Длина зубьев ведущей шестерни:
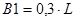 , ,
где L - длина образующей делительного конуса, L=180 .
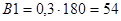 мм. мм.
Длина зубьев ведомой шестерни:
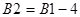 ; ;
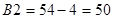 мм. мм.
Угол наклона винтовой линии (BET 1), угол наклона винтовой линии (BET 2), смещение осей (Е), угол зацепления (AL), коэффициент динамичности (Kd) выбраны согласно рекомендациям в [2, стр. 249, таб.11.1].
Передаточное число первой передачи (U1), передаточное число раздаточной коробки (Up), радиус качения колеса (Ro), расчётный крутящий момент (Mtr), максимальный крутящий момент (Me max) выбраны согласно данным производителя [1].
Число зубьев ведущей шестерни (Z1), число зубьев ведомой шестерни (Z2) выбраны согласно рекомендациям в [2, стр. 249, таб.11.1].
4.3 Проведение расчета
Таблица 7 - Исходные данные для расчета главной передачи
| Длина образующей делительного конуса ( L ), мм |
180 |
| Число зубьев ведущей шестерни ( Z1 ) |
9 |
| Число зубьев ведомой шестерни ( Z2 ) |
32 |
| Угол наклона винтовой линии (BET 1 ), град |
51,17 |
| Угол наклона винтовой линии (BET 2 ), град |
26,15 |
| Смещение осей ( Е ), мм |
31,75 |
| Длина зубьев ведущей шестерни ( B1 ), мм |
54 |
| Длина зубьев ведомой шестерни ( B2 ), мм |
50 |
| Угол зацепления ( AL ), трад |
16 |
| Передаточное число первой передачи ( U1 ) |
3,67 |
| Передаточное число раздаточной коробки ( Up ) |
2.135 |
| Радиус качения колеса (Ro), мм |
330 |
| Коэффициент динамичности ( Kd ) |
1,5 |
| Расчётный крутящий момент ( Mtr ), Н*м |
114 |
| Максимальный крутящий момент ( Me max ), Н*м |
114 |
Таблица 8 - Результаты расчета главной передачи
| Радиус средней точки зуба (Rср), мм |
41,42 |
| Радиус средней точки зуба (Rср), мм |
106,6 |
| Половина угла при вершине начального конуса (DEL1), град |
16,13 |
| Половина угла при вершине начального конуса (DEL2), град |
76,27 |
| Радиус кривизны зуба (Ro1), мм |
27,8 |
| Радиус кривизны зуба (Ro2), мм |
129,8 |
| Эквивалентное число зубьев (Ze1) |
34,86 |
| Эквивалентное число зубьев (Ze2) |
160,6 |
| Торцевой шаг по основанию конуса (Ts1), мм |
32,76 |
| Торцевой шаг по основанию конуса (Ts2), мм |
23,4 |
| Окружная сила (P1), Н |
2,752 |
| Окружная сила (P2), Н |
1,07 |
| Осевая сила (Q1), Н |
3,462 |
| Осевая сила (Q2), Н |
0,456 |
| Радиальная сила (Rs1), кН |
2,029 |
| Радиальная сила (Rs2), кН |
0,5799 |
| Напряжение изгиба (SIG изг 1), МПа |
1,765 |
| Напряжение изгиба (SIG изг 2), МПа |
0,4287 |
| Напряжение смятия (SIG см 1), МПа |
113,2 |
| Напряжение смятия (SIG см 2), МПа |
73,36 |
| Ресурс главной передачи, тыс. км. |
1,99E+05 |
Ресурс главных передач до капитального ремонта лежит в пределах 125…250 тыс. км. пробега для легковых автомобилей, следовательно рассчитанная главная передача имеет малый ресурс, но в целом удовлетворяет установленным требованиям.
5 Расчет полуоси
5.1 Алгоритм расчета полуоси
Для полностью разгруженной полуоси определяют только напряжении кручения.
1. При прямолинейном движении: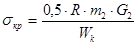 , ,
где R - величина нормальной реакции на внутренний конец полуоси со стороны дифференциала.
m2 - максимальное значение коэффициента перераспределения веса.
G2 – вес, приходящийся на задний мост.
Wк = 0.2·D3
- момент сопротивления при кручении.
2. При динамической нагрузке: 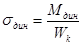
где 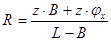 , ,
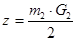
B -расстояние от середины внешнего опорного подшипника до вертикали проходящей через центр опорной площадки колеса.
L – длина полуоси.
Mдин = 0,5 · Ме · i1 · i0 · kд(1+kб) - максимальный момент, передаваемый полуосью ведущего моста.
Ме - максимальный момент двигателя, Н*м;
i1, i0 - передаточные числа первой и главной передачи ;
Kд - коэффициент динамичности (Kд=1...1,3);
КБ- коэффициент блокировки.
для дифференциала с малым внутренним трением КБ = 0,1...0,2;
повышенного трения КБ = 0,2...0,6
блокированного КБ до 1.
5.2 Обоснование выбора исходных данных
Коэффициент перераспределения веса, расчётный коэффициент продольного сцепления, расчётный коэффициент поперечного сцепления, коэффициент динамичности, момент, подводимый к полуоси выбраны согласно рекомендациям в [3].
Вес, приходящийся на рассчитываемый мост, радиус колеса, колея автомобиля выбраны согласно данным в [1].
Диаметр полуоси, расстояние от середины внешнего опорного подшипника до вертикали, длина полуоси выбраны согласно рекомендациям в [4, стр. 143].
5.3 Проведение расчета
Таблица 9 - Исходные данные для расчета полуоси
| Вес, приходящийся на рассчитываемый мост, Н |
7500 |
| Коэффициент перераспределения веса |
1,2 |
| Расчётный коэффициент продольного сцепления |
0,8 |
| Расчётный коэффициент поперечного сцепления |
1 |
| Колея автомобиля, мм |
1400 |
| Коэффициент динамичности |
1,2 |
| Диаметр полуоси, мм |
28 |
| Расстояние от середины внешнего опорного подшипника до вертикали, мм |
80 |
| Длина полуоси, мм |
605 |
| Радиус колеса, мм |
330 |
| Момент подводимый к полуоси, Н*м |
114 |
Таблица 10 -Результаты расчета полуоси
| Максимальные суммарные напряжения, МПа |
225,49 |
| Максимальный угол закручивания, град |
0,77121 |
| Ресурс полуоси, тыс. км. |
13151 |
Обратившись к [3] можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям и данная полуразгруженная полуось годна к эксплуатации.
Упругий элемент подвески выполняющий одновременно функции упругого элемента, направляющего устройства и гасящего устройства.
6.1 Алгоритм расчета многолистовой рессоры
Зная ориентировочное число листов n и число листов, равных по длине коренному листу n1, определяют:
1) Коэффициент формы рессоры:
B = 1 - 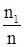 ; ;
2) Коэффициент увеличения прогиба:
I = 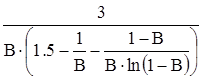 . .
Длина коренных листов:
L = 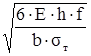 , ,
где: Е - модудь упругости, (Е=20.5·104
МПа);
f - статический прогиб рессоры, определяемый по выбранному числу колебаний подрессоренной массы nk;
Параметры рессоры:
1) Момент инерции рессоры:
J = 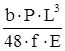 ; ;
где: Р - нагрузка на упругий элемент.
2) Число листов рессоры:
n = 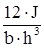 ; ;
3) Значение наибольшего напряжения:
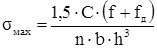 ; ;
где: fд
- динамический прогиб рессоры.
Для получения удовлетворительной емкости подвески значение fД
следует принимать равными, а если это допустимо по конструктивным возможностям то больше, чем статический прогиб f.
Вес рессоры рассчитываем по формуле:
Gp
= 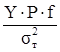
где: Y - постоянная, зависящая от формы рессоры.
Жесткость рессоры определяется по формуле:
C = P/f.
6.2 Обоснование выбора исходных данных
Коэффициент увеличения прогиба (I), коэффициент динамичности (KЯ
), модуль упругости при растяжении (Е), длина активного участка рессоры (L) выбраны согласно рекомендациям в [5].
Нагрузка на рессору (Р), нагрузка на упругий элемент (Р), средняя скорость движения автомобиля (Vср
) выбраны согласно данным в [3].
Число циклов нагружения, статический коэффициент прогиба (Dd
), выбраны согласно рекомендациям в [4].
Длина рессоры (L), ширина рессоры (В), толщина рессоры (Н), число листов, равных по длине коренному листу (Nk
) выбраны согласно рекомендациям в [2].
6.3 Проведение расчета
6.3.1 Расчет малолистовой рессоры
Таблица 11 - Исходные данные для расчета малолистовой рессоры
| Нагрузка на рессору ( Р ), Н |
3855 |
| Длина рессоры ( L ), м |
0,6 |
| Модуль упругости ( Е ), МПа |
201000 |
| Коэффициент увеличения прогиба ( I ) |
1,75 |
| Ширина рессоры ( В ), м |
0,06 |
| Толщина рессоры ( Н ), м |
0,01 |
Таблица 12 - Результаты расчета малолистовой рессоры
| Жёсткость рессоры, МПа |
0,01108 |
| Статический прогиб, м |
0,38639 |
| Напряжение в заделке, МПа |
216,33 |
| Объём рессоры, м^3 |
0,23057 |
| Удельная энергия деформации, Дж/м^3 |
37141 |
Обратившись к [2] и [3], можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям.
6.3.2 Проверочный расчет малолистовой рессоры
Таблица 13 - Исходные данные для проверочного расчета
| Число листов рессоры ( N ) |
3 |
| Ширина листов рессоры ( B ), м |
0,06 |
| Толщина листов рессоры ( Н ), м |
0,01 |
| Коэффициент динамичности ( K z), м |
1,8 |
| Число циклов нагружения * 10^6 ( Nb ) |
2 |
| Статический коэффициент прогиба ( Dd) |
1,3 |
| Модуль упругости при растяжении ( Е ), ГПа |
210 |
| Длина активного участка рессоры ( L ), м |
0,6 |
| Число листов, равных по длине коренному листу (Nk ) |
1 |
| Нагрузка на упругий элемент ( Р ), Н |
3855 |
| Средняя скорость движения автомобиля ( Vср ), км/ч |
60 |
Таблица 14 - Результаты проверочного расчета
| Напряжение изгиба рессоры, МПа |
17,089 |
| Статический прогиб рессоры, м |
0,058751 |
| Динамический прогиб рессоры, м |
0,051001 |
| Общий прогиб рессоры, м |
0,10375 |
| Низшая частота собственных колебаний, Гц |
1,7011 |
| Жёсткость рессоры, Кн/м |
51,944 |
| Долговечность рессоры, тыс. км |
49,11 |
Обратившись к [8] и [3], можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям и данная малолистовая рессорная подвеска годна к эксплуатации.
7 Расчет амортизатора
Амортизатор - упругий элемент подвески.
7.1 Алгоритм расчета амортизатора
Поглощаемая мощность:
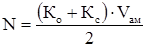 . .
Максимальные усилия передаваемые через амортизатор:
Ро
= Ко
· Vам
,
Ро
= Ко
· Vам
.
Площадь наружной поверхности амортизатора:
F = 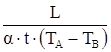 . .
Диаметр рабочего цилиндра:
D = 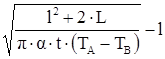 . .
Площади поперечных сечений калиброванных отверстий клапанов отдачи и сжатия:
Fo
= Vам
· 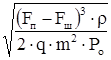 , ,
Fo
= Vам
· 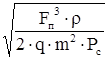 , ,
где, Fп
и Fш
– площади поперечных сечений поршня и штока, они могут быть приняты:
Fп
= 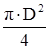 , ,
Fш
= 0,1 · Fп
.
7.2 Обоснование выбора исходных данных
Коэффициент сопротивления амортизатора при отдаче, коэффициент сопротивления амортизатора при сжатии, скорость перемещения поршня амортизатора, температура окружающей среды, время работы амортизатора, плотность жидкости, температура окружающей среды, коэффициент расхода жидкости, проходящей через калиброванные отверстия, длина амортизатора, максимальная температура наружних стенок амортизатора, время работы амортизатора взяты из [7].
Длина амортизатора, диаметр амортизатора выбраны согласно рекомендациям в [7].
7.3 Проведение расчета
7.3.1 Проведение проектировочного расчета
Таблица 13 - Исходные данные для проектировочного расчета
| Коэффициент сопротивления амортизатора при отдаче, кН*с/м |
0,6 |
| Коэффициент сопротивления амортизатора при сжатии, кН*с/м |
0,1 |
| Скорость перемещения поршня амортизатора, м/с |
0,3 |
| Коэффициент теплоотдачи, Вт/м^2*К |
0,7 |
| Максимальная температура наружних стенок амортизатора, К |
493 |
| Температура окружающей среды, К |
297 |
| Коэф-т расхода жидкости, проходящей через калиброванные отверстия |
0,09 |
| Плотность жидкости, кг/м^3 |
0,0007 |
| Длина амортизатора, м |
0,39 |
| Время работы амортизатора, с |
3200 |
Таблица 14 - Результаты проектировочного расчета
| Работа амортизатора, Дж |
6,37E+05 |
| Площадь поверхности амортизатора, м^2 |
0,272 |
| Диаметр амортизатора, м |
0,1317 |
| Площадь поршня, м^2 |
0,0219 |
| Площадь сечения штока, м^2 |
0,00216 |
| Площадь отверстия клапана отдачи, см^2 |
2,52E-16 |
| Площадь сечения клапана сжатия, см^2 |
3,82E-09 |
| Поглощаемая мощность, Вт |
198,5 |
Обратившись к [4], можно сделать вывод, что результаты проектировочного расчета удовлетворяют установленным требованиям.
7.3.2 Проведение проверочного расчета
Таблица 15 - Исходные данные для проверочного расчета
| Длина амортизатора, м |
0,39 |
| Диаметр амортизатора, м |
0,14 |
| Плотность жидкости, кг/м^3 |
0,0009 |
| Температура окружающей среды, К |
297 |
| Коэффициент сопротивления амортизатора при отдаче, кН*с/м |
0,6 |
| Коэффициент сопротивления амортизатора при сжатии, кН*с/м |
0,1 |
| Скорость перемещения поршня амортизатора, м/с |
0,3 |
| Коэффициент теплоотдачи, Вт/м^2*К |
0,7 |
| Коэф-т расхода жидкости, проходящей через калиброванные отверстия |
0,09 |
| Время работы амортизатора, с |
3200 |
Таблица 16 - Результаты проектировочного расчета
| Работа амортизатора, кДж |
637 |
| Поглощаемая мощность, Вт |
198,5 |
| Площадь поверхности амортизатора, м^2 |
0,284 |
| Максимальная температура наружных стенок амортизатора, К |
493 |
Обратившись к [4], можно сделать вывод, что результаты проверочного расчета удовлетворяют установленным требованиям и амортизатор годен к эксплуатации.
8 Расчет пружины
Пружина – упругий элемент подвески.
8.1 Алгоритм расчета пружины
При подборе пружины используются следующие основные зависимости:
Жёсткость пружины:
су
= 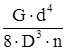 ; ;
где: G - модуль упругости второго рода;
d - диаметр сечения витка;
D - средний диаметр пружины;
n - число рабочих витков.
Напряжения сдвига:
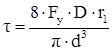 ; ;
где: Fy - статическая нагрузка;
Полное число витков:
N = n+2.
Средний диаметр пружины:
D = d·(7...12).
8.2 Обоснование выбора исходных данных
Модуль упругости сдвига примем равным 78000 МПа.
Нагрузка на упругий элемент, прогиб пружины, диаметр проволоки, число рабочих витков пружины выбраны согласно данным в [7].
8.3 Проведение расчета
Таблица 17 - Исходные данные для расчета пружины
| Нагрузка на упругий элемент ( P ), Н |
4300 |
| Модуль упругости сдвига, МПа (рекомендуется брать 78000 МПа) |
78000 |
| Прогиб пружины ( F ), м |
0,00864 |
| Диаметр проволоки ( в ), м |
0,15 |
| Число рабочих витков пружины ( I ) |
6 |
Таблица 18 - Результаты расчета пружины
| Жёсткость пружины, Н/м |
0,54697 |
| Полное число витков пружины |
8 |
| Средний диаметр пружины, м |
1,2 |
Обратившись к [3], можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям и пружина годна к эксплуатации.
9 Расчет рулевого управления
9.1 Алгоритм расчета рулевого управления
1. Угловое передаточное число рулевого управления определяется по соотношению углов поворота рулевого колеса и управляемых колес , выраженному уравнением:
i0
= 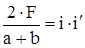 , ,
где: F - угол поворота рулевого колеса ;
a, b - углы поворота управляемых колес;
i, i' - угловое передаточное число рулевого механизма и рулевого привода.
2. Силовое передаточное число рулевого управления (ip) определяется из равенства работ на рулевом колесе и управляемых колесах :
P · R · F =  , ,
где R - радиус рулевого колеса;
r - радиус поворота управляемых колес;
Q - сопротивление колес повороту.
Отсюда:
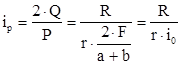
Конструкция рулевого механизма и его особенности, например, передаточное число, в большой степени влияют на манёвренность автомобиля, но недостаточно полно характеризуют её, так как не учитываю времени поворота автомобиля. Поэтому в добавление к ним в качестве одного из оценочных параметров нужно принять время t в течение, которого происходит поворот автомобиля.
3. Время поворота автомобиля (t), c:
t = 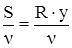 , ,
где S - длина траектории поворота;
v - поступательная скорость автомобиля на повороте;
R - радиус поворота (по центру заданной оси;
y - угол заданной оси.
9.2 Обоснование выбора исходных данных
Радиус рулевого колеса ( R ), радиус поворота управляемых колёс ( R1 ), длина траектории поворота ( S ), поступательная скорость автомобиля на повороте ( Va ), усилие прилагаемое к рулевому колесу ( Pk ), максимальное давление в системе усилителя (Pmax), масса автомобиля, приходящаяся на передние колёса выбраны согласно данным в [4 ].
Угол поворота рулевого колеса (F), угол поворота правого управляемого колеса (а), угол поворота левого управляемого колеса (b) выбраны согласно рекомендациям в [1].
9.3 Проведение расчета
Таблица 19 - Исходные данные для расчета рулевого управления
| Угол поворота рулевого колеса ( F ), град |
740 |
| Угол поворота правого управляемого колеса ( а ), град |
38 |
| Угол поворота левого управляемого колеса ( b ), град |
38 |
| Радиус рулевого колеса ( R ), м |
0,17 |
| Радиус поворота управляемых колёс ( R1 ), м |
5,5 |
| Длина траектории поворота ( S ), м |
9 |
| Поступательная скорость автомобиля на повороте ( Va ), м/с |
7 |
| Усилие прилагаемое к рулевому колесу ( Pk ), кг |
16 |
| Рабочий объём силового цилиндра усилителя ( V ), м^3 |
0,56 |
| Максимальное давление в системе усилителя (Pmax), кг/м^2 |
0,71 |
| Масса автомобиля, приходящаяся на передние колёса, кг |
750 |
| Площадь поршня силового цилиндра, м^2 |
0,56 |
Таблица 20 - Результаты расчета рулевого управления
| Угловое передаточное число рулевого управления |
20 |
| Силовое передаточное число рулевого управления |
0,76 |
| Время поворота автомобиля, с |
1,25 |
| Эффективность по удельному усилию усилителя, Н/кг |
0,00455 |
| Коэф-т удельного объёма силового цилиндра усилителя, м^3/кг |
0,005175 |
| Коэффициент мощности силового цилиндра, Н*м |
0,2895 |
Обратившись к [2], можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям и рулевое управление годно к эксплуатации.
10 Расчет тормозного управления
10.1 Алгоритм расчета тормозного управления
Коэффициент тормозной эффективности - это отношение тормозного момента, создаваемого тормозным механизмом, к условному приводному моменту:
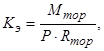
где Мтор - тормозной момент, H*м;
Р - сумма приводных сил, H;
Rтор - радиус приложения результирующей сил трения, м.
Стабильность. Этот критерий характеризует зависимость коэффициента
тормозной эффективности от изменения коэффициента трения.
Лучшей стабильностью обладают тормозные механизмы, характеризуемые линейной зависимостью. Уравновешанными являются тормозные механизмы, в которых силы трения не создают нагрузки на подшипники колеса.
Установившиеся замедление Jуст определяется:
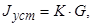
где к - коэффициент сцепления колеса с дорогой;
G - вес автомобиля, H.
Минимальный тормозной путь S определяется:

где V - начальная скорость автомобиля, м/c;
tc - время запаздывания тормозов, c;
tn - время наростания замедления,c;
g - ускорение свободного падения, m/c^2;
По ГОСТ 22859-97,S для легковых и грузовых автомобилей соответственно 7,2м, 25м.
Суммарная тормозная сила P, (H) определяется:
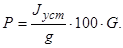
Тормозной момент Мт, (H*м) определяется:
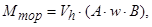
где Vh - рабочий объем двигателя, л
A,B - коэффициенты корректировки;
w - частота вращения коленвала, рад/с.
10.2 Обоснование выбора исходных данных
Число тормозных механизмов автомобиля, динамический радиус колеса, радиус тормозного барабана, толщина стенки барабана, ширина фрикционных накладок передних колёс, ширина фрикционных накладок задних колёс, суммарная площадь фрикционных накладок, диаметр рабочего тормозного гидроцилиндра, полный вес автомобиля, масса автомобиля, приходящаяся на тормозящую ось выбраны согласно рекомендациям в [4].
Максимальный тормозной момент передних колёс, максимальный тормозной момент задних колёс рассчитаны согласно рекомендациям в [2].
Угол охвата фрикционных накладок переднего моста, угол охвата фрикционных накладок заднего моста, расчётный коэффициент трения, скорость движения автомобиля при торможении выбраны согласно рекомендациям в [2].
Нижний предел максимального замедления, расстояние от линии действия разжимных сил до опоры, расстояние от центра барабана до оси опоры, углы несимметричности накладок передних колёс, углы несимметричности накладок задних колёс, масса барабана, удельная теплоёмкость чугуна выбраны согласно рекомендациям в [3].
10.3 Проведение расчета
10.3.1 Проектировочный расчет
Таблица 21- Исходные данные для проектировочного расчета тормозного управления
| Полный вес автомобиля, Н |
16500 |
| Число тормозных механизмов автомобиля |
4 |
| Скорость автомобиля, м/с |
8,5 |
| Динамический радиус колеса, м |
0,33 |
| Нижний предел максимального замедления, м/с^2 |
8 |
| Расстояние от линии действия разжимных сил до опоры, м |
0,1325 |
| Радиус тормозного барабана, м |
0,1443 |
| Толщина стенки барабана, м |
0,021 |
| Расстояние от центра барабана до оси опоры, м |
0,047 |
| Углы охвата фрикционных накладок передних колёс, град |
100 |
| Углы охвата фрикционных накладок задних колёс, град |
100 |
| Углы несимметричности накладок передних колёс, град |
30 |
| Углы несимметричности накладок задних колёс, град |
30 |
| Ширина фрикционных накладок передних колёс, м |
0,1 |
| Ширина фрикционных накладок задних колёс, м |
0,1 |
| Суммарная площадь фрикционных накладок, м^2 |
0,191 |
| Плечо приложения разжимных сил, м |
0 |
| КПД кулачкового привода |
0 |
| Эффективная площадь диафрагмы тормозной камеры или цилиндра, м^2 |
0 |
| Длина приводного рычага кулачкового вала, м |
0 |
| Диаметр рабочего тормозного гидро-, пневмо- цилиндра, м |
0,0248 |
| Максимальный тормозной момент передних колёс, Н*м |
25,038 |
| Максимальный тормозной момент задних колёс, Н*м |
25,038 |
Таблица 22 - Результаты расчета тормозного управления
| Необходимые значения тормозных моментов передних колёс, Н*м |
880,1 |
| Необходимые значения тормозных моментов задних колёс, Н*м |
1787 |
| Разжимные силы передних торм. механизмов (самоприжимная колодка), кН |
2095 |
| Разжимные силы передних торм. механизмов (самоотжимная колодка), кН |
-2095 |
| Разжимные силы задних торм. механизмов (самоприжимная колодка), кН |
4254 |
| Разжимные силы задних торм. механизмов (самоотжимная колодка), кН |
-4254 |
| Максимальное значение давления воздуха (на передних колёсах), кН/м^2 |
0 |
| Максимальное значение давления воздуха (на задних колёсах), кН/м^2 |
0 |
| Максимальное значение давления жидкости (на передних колёсах), кН/м^2 |
4,52E+06 |
| Максимальное значение давления жидкости (на задних колёсах), кН/м^2 |
9,18E+06 |
| Удельная работа трения, Дж |
2,46E+04 |
| Удельная мощность трения, Вт |
1,67E+05 |
| Повышение температуры тормозного барабана, град С |
0 |
| Повышение температуры передних колёс, град С |
1,48E+06 |
| Повышение температуры задних колёс, град С |
1,48E+06 |
| Среднее удельное давление между барабаном |
0 |
| и тормозными накладками передних колёс, Н/м^2 |
343,6 |
| и тормозными накладками задних колёс, Н/м^2 |
343,6 |
| Коэффициент KF |
8,64E+04 |
Обратившись к [4], можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям.
11 Расчет несущей части автомобиля
11.1 Алгоритм расчета несущей части автомобиля
Предельные динамические нагрузки характеризуются коэффициентом динамической нагрузки:
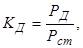
где Рд - динамическая нагрузка на раму,
Рст - статическая нагрузка.
Значения коэффициентов динамической нагрузки:
- для грузовых автомобилей: 2...2,5;
- для автобусов: 1,5...2;
- для легковых автомобилей: 1,1...1,5.
При движении по неровной дороге в раме возникают изгибающие и крутящие нагрузки. Суммарный перекос ALF передней и задней оси вызывает угловую деформацию передней и задней подвески автомобиля на угол ALFп и закручивание рамы на угол ALFр, измеренный на длине базы автомобиля, при этом:
ALFп + ALFр = ALF,
где ALFп = Mкр/Cп;
ALFр = Mкр/Cp;
Cп - угловая жесткость подвески;
Ср - жесткость рамы.
Отсюда:
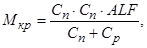 Н*м; Н*м;
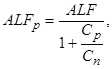 град. град.
Величина Сп/Ср для грузовых автомобилей около 0,5...1,5;
для автобусов и легковых автомобилей более 4.
ALFр = 3...4 градуса при движении по неровным дорогам, но при отрыве колес от поверхности дороги рама может закручиваться на угол до 10...15 градусов.
В этом случае:
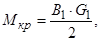
где В1 - колея, м;
G1 - нагрузка на ось, Н.
При кручении рамы лонжероны и поперечены испытывают сложное нагрузочное состояние: поперечные сечения становятся неплоскими (явление депланации сечений). Мера депланации:
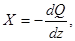
где dQ - угол закручивания;
z - расчетная длина при закручивании.
Возникающие при стесненном кручении нормальные напряжения выражаются через особый силовой фактор - бимомент:
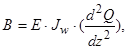
При введении понятия бимомента основные формулы изгиба и стесненного кручения аналогичны и приведены ниже.
11.2 Обоснование выбора исходных данных
Колея автомобиля ( В1 ), база автомобиля ( Z ), нагрузка на ось ( G1 ) выбраны согласно данным в [1].
Толщина полки профиля ( S ), высота профиля ( H ), ширина полки профиля ( В ), момент сопротивления изгибу ( WX
) выбраны согласно рекомендациям в [3].
11.3 Проведение расчета
Таблица 25 - Исходные данные для расчета несущей части
| Колея автомобиля ( В1 ), м |
1,400 |
| База автомобиля ( Z ), м |
2,200 |
| Нагрузка на ось ( G1 ), Н |
7500 |
| Толщина полки профиля ( S ), м |
0,004 |
| Высота профиля ( H ), м |
0,17 |
| Ширина полки профиля ( В ), м |
0,052 |
| Момент сопротивления изгибу ( WX ), м^3 |
3,73E-05 |
Таблица 26 - Результаты расчета несущей части
| Суммарное напряжение, МПа |
442,4 |
| Момент инерции сечения при кручении, м^4 |
6,36E-09 |
| Секториальный момент инерции , м^5 |
3,10E-07 |
| Максимальный крутящий момент, кН*м |
5,25 |
| Изгибающий момент, кН*м |
16,5 |
| Угол закручивания рамы, град |
6,077 |
Обратившись к [4], можно сделать вывод, что результаты расчета удовлетворяют установленным требованиям и несущая часть (рама) годна к эксплуатации.
Литература
1. Автомобили ВАЗ 21213, 21214. Руководство по ремонту и техническому обслуживанию / Под ред. Ю.В. Кудрявцева, М.: РусьАвтокнига, 2004.-304 с.
2. Справочник “Проектирование трансмиссии автомобиля”, под ред. Гришкевича А.И. ,М. :Машиностроение, 1984-272 с., ил.
3. Лукин П.П и др. “Конструирование и расчет автомобиля”, М,: Машиностроение, 1984-376 сю,ил.
4. Осепчугов В.В. Фрумкин А.К. “Автомобиль’ М, :Машиностроение, 1989.-304 с, ил.
5. Справочный материал программы Auto V2.0.
|