Реферат: Задачі нелінійного програмування. Деякі основні методи їх розвязування та аналізу
|
Название: Задачі нелінійного програмування. Деякі основні методи їх розвязування та аналізу Раздел: Рефераты по информатике Тип: реферат |
| Реферат на тему: Задачі нелінійного програмування. Деякі основні методи їх розв’язування та аналізу. План. 1. Метод Франка-Вулфа. 2. Приклади розв’язування задач. 3. Література Деякі з основних методів розв’язування задач НЛП. 1. Метод Франка –Вулфа . Нехай потрібно найти максимальне значення вогнутой функції
при умовах : Характерною особливістю цієї задачі являється то , що її система обмеження вміщує тільки лінійні нерівності . Ця особливість являє основний для заміни в межах досліджуваної точки нелінійної цільової функції лінійною , завдяки чому розв’язок даної задачі зводиться до послідовного розв’язку задач лінійного програмування. Процес найдення розв’язку задачі начинають з оприділення точки , принадлежавшої області допустимих розв’язків задачі. Нехай ця точка
і будують лінійну функцію (60) Потім знаходять максимальне значення цієї функції при обмеженнях (58) і (59). Нехай рішення даної задачі визначається точкою де залежавши від Отже, процес находження розв’язків задачі (57) – (59) методом Франка – Вулфа включає наступні етапи : 1. Визначають даний допустимий розв’язок задачі . 2. Находять градієнт функції (57) в точці допустимого розв’язку . 3. Будують функцію (60) і находять її максимальне значення при умовах (58) і (59) . 4. Визначають крок обчислень . 5. По формулам (61) находять компоненти нового допустимого розв’язку . 6. Провіряють необхідність переходу до наступного допустимого розв’язку . У випадку необхідності переходять до етапу 2 , в поганому випадку найдене прийняте розв’язок даної задачі . 3.27. Методом Франка – Вулфа найти розв’язок задачі 3.22. , забезпеченої в певному максимальному значенні функції
при умовах
Розв’язок . Найдем градієнт функції і в якості даного допустимого розв’язку задачі візьмемо точку 1. Ітерація . В точці при умовах (63) і (64) Задача (65)—(67) має оптимальний план Найдемо новий допустимий розв’язок даної задачі по формулі (61): Підставимо замість Знайдемо тепер число із значення у відповідності з відношенням (69) знайдемо подібну цій функції по
Оскільки найдене значення
2. Ітерація . Градієнт цільової функції даної задачі в точці Оприділяєм тепер Підкладемо тепер в функцію (62) замість звідки т.е. 3. Ітерація . Градієнт функції f в точці Знайдемо Розв’язуючи рівність Таким образом , Література. 1. Наконечний С.І., Савіна С.С. Математичне програмування: Навч. посіб. – К.:КНЕУ, 2003.- 452 с. 2. Барвінський А.Ф та ін. Математичне програмування: Навчальний посібник / А.Ф. Барвінський, І.Я. Олексів, З.І. Крупка, І.О. Бобик, І.І. Демків, Р.І. Квіт, В.В. Кісілевич – Львів: Національний університет “Львівська політехніка” (Інформаційно-видавничий центр “Інтелект+” Інститут післядипломної освіти) “Інтелект - Захід”, 2004. – 448 с. 3. Акулич М.Л. Математичиское програмирование в примерах и задачах: Учебное пособие для студентов экономических специальних вузов. – Вища школа, 1985-319с.,ст.270-274. 4. Вітлінський В.В., Наконечний С.І., Терещенко Т.О. Математичне програмування: Навч. – метод. посібник для самост. вивч. дисц. – К.: КНЕУ, 2001. – 248 с. 5. Математичне програмування (методичний посібник для студентів економічних спеціальностей)/Укладачі: Лавренчук В.П., Веренич І.І., Готинчан Т.І., Дронь В.С., Кондур О.С., - Чернівці: „Рута”, 1998.-168 с. |
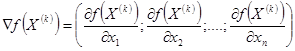
 (63) (64)
(63) (64) 
 (66)
(66) 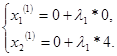 (69)
(69)


