| |
Выполнили:
Дудорова А.С.
Ажиба Н.Р.
Гр. 4074/20
|
Лабораторная работа по эконометрике № 1
Необходимо выполнить следующие задания по 2-м показателям:
- Объём промышленной продукции за 2008 год;
-Основные фонды за 2008 год.
1. Определить какой из 2-х показателей является результирующим показателем (Уi), а какой факторным признаком, влияющим на результат (Хi).
2. Построить точечную диаграмму зависимости Х от У. Сделать вывод. Определить, как зависят друг от друга показатели.
3. Построить линейное уравнение регрессии. Сделать выводы по уравнению. Провести регрессионную статистику и дисперсионный анализ в таблицах. Сделать по ним выводы.
4. Посчитать остатки и сделать графики зависимостей остатков. Выводы.
5. Проверить гипотезу об отсутствии автокорреляции остатков.
6. Провести 2-а теста по оценке гетероскапичности.
7. Посчитать вручную коэф-т детерминации и проверить равенство:

8. Посчитать вручную все ошибки.
Решение:
1. Основные фонды – факторный признак, влияющий на результат (Хi). Объём промышленной продукции - результирующим показателем (Уi).
Таблица 1.
Социально - экономические показатели по регионам России в 2008 г.
| Регионы России
|
Основные фонды в экономике (по полной учетной стоимости; на конец года), млн. руб. (Х)
|
Объём промышленной продукции, млн.руб. (У)
|
| Белгородская область
|
507024
|
350134
|
| Брянская область
|
327029
|
82119
|
| Владимирская область
|
328569
|
179771
|
| -//-//-//-
|
-//-//-//-
|
-//-//-//-
|
Всего регионов 79.
2. Зависимость Х от У.
Диаграмма 1
Точечная диаграмма зависимости результирующего показателя от факторного признака, влияющего на результат.
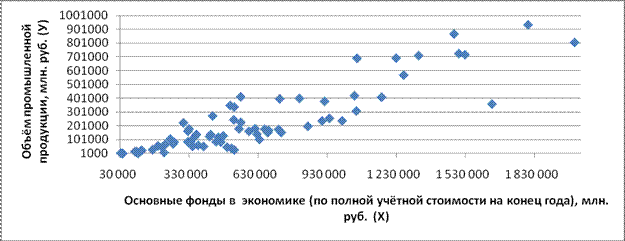
С увеличением основных фондов в экономике по регионам России, в среднем увеличивается объём производства продукции по регионам России за 2008 год. Зависимость прямая.
3. Линейное уравнение регрессии выглядит следующим образом: 
Приведу регрессионную статистику и дисперсионный анализ в таблицах:
Таблица 2
Регрессионная статистика
| Множественный R
|
0,92
|
| R-квадрат
|
0,85
|
| Нормированный R-квадрат
|
0,58
|
| Стандартная ошибка
|
197016
|
| Наблюдения
|
79
|
Выводы:
- коэф-т корреляции (Множественный R) составляет 0,92 %. Это означает, что между показателями существует сильная зависимость.
- коэф-т детерминации (R-квадрат) составляет 0,85 %. Показывает, что объём промышленной продукции на 85% объясняется изменением основных фондов.
-расчётные значения объёма промышленной продукции отличаются от фактических в среднем на 197016 млн. руб.
Таблица 3
Дисперсионный анализ
| |
df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия
|
1
|
1,74073E+13
|
1,74073E+13
|
448,468
|
7,58E-34
|
| Остаток
|
77
|
2,98876E+12
|
38815122108
|
|
|
| Итого
|
78
|
2,03961E+13
|
|
|
|
 = 448 = 448
 = 3,97 по Фишеру через функцию (=FРАСПОБР(0,05;k-1;n-k)) = 3,97 по Фишеру через функцию (=FРАСПОБР(0,05;k-1;n-k))
 > >  , подтверждается гипотеза о наличии зависимости. , подтверждается гипотеза о наличии зависимости.
Вывод: Из таблицы дисперсионного анализа видно с вероятностью 95% , что построенное уравнение адекватно. Наличие зависимости доказано.
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
| Y-пересечение
|
84124
|
24649
|
3,4129165
|
0,001
|
35042
|
133205,47
|
35042
|
133205
|
| Основные фонды в экономике, млн. руб. (Х)
|
0,24
|
0,01144368
|
21,177063
|
7,58E-34
|
0,2195
|
0,2651309
|
0,2195
|
0,2651
|
Выводы:
- Клэф -т 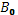 и и 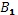 значим, т.к. одинаковые знаки в границах. значим, т.к. одинаковые знаки в границах.
- С вероятностью 95% при увеличении основных фондов на 1 млн. руб. объём промышленной продукции увеличиваются в среднем величину от 220 - 260 млн. руб.
Готовое линейное уравнение выглядит так: 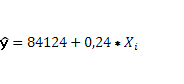
Вывод: При увеличении основных фондов на 1 млн. руб. объём промышленной продукции увеличивается в среднем на 240 000 млн. руб.(0,24)
4. Построю графики зависимостей остатков.
Расчётные значения.
| Регионы России
|
Основные фонды в экономике (по полной учетной стоимости; на конец года), млн. руб. (Х)
|
Объём промышленной продукции, млн.руб. (У)
|
Расчётные значения (
 ) )
|
Ei (остаток) =
|
| Белгородская область
|
507024
|
350134
|
206998
|
143136
|
| Брянская область
|
327029
|
82119
|
163377
|
-81258
|
| -//-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
| Еврейская автономная область
|
104532
|
6110
|
109456
|
-103346
|
График зависимости факторного признака и остатков.

График зависимости расчётного значения результирующего показателя и остатков.

5. Проверка гипотезы об отсутствии автокорреляции остатков.
 ; автокорреляция остатков отсутствует ; автокорреляция остатков отсутствует
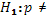 0;
автокорреляция остатков присутствует 0;
автокорреляция остатков присутствует
Автокорреляция остатков (r) рассчитывается через функцию = КОРРЕЛ (выделяются остатки с первого по предпоследний; выделяются остатки со второго до последнего)
r = 0,24
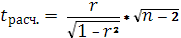 = =  = 2,14 = 2,14
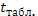 по функции = СТЬЮДРАСПОБР (0,05;78-2) = 1,99 по функции = СТЬЮДРАСПОБР (0,05;78-2) = 1,99
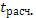 > > 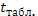 ; принимается гипотеза ; принимается гипотеза 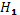 , т.е. с вероятностью 95 % автокорреляция в остатках присутствует. , т.е. с вероятностью 95 % автокорреляция в остатках присутствует.
6. Проведу 2-а теста по оценке гетероскапичности.
- 1-ый тест:
| Регионы России
|
Основные фонды в экономике (по полной учетной стоимости; на конец года), млн. руб. (Х)
|
Объём промышленной продукции, млн.руб. (У)
|
Расчётные значения (
 ) )
|
Ei (остаток) =
|
Ei по модудю
|
Ранги по (Х)
|
Ранги по модулю остатка
|
| Белгородская область
|
507024
|
350134
|
206998
|
143136
|
143136
|
41
|
18
|
| Брянская область
|
327029
|
82119
|
163377
|
-81258
|
81258
|
57
|
50
|
| -//-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
-//-//-
|
| Еврейская автономная область
|
104532
|
6110
|
109456
|
-103346
|
103346
|
74
|
32
|
Всего регионов 79.
Коэф-т корреляции (r) между рангами равен 0,85 %. Находится по функции = КОРРЕЛ (массив данных рангов по Х; массив данных рангов по модулю остатка)
Вывод: Объём промышленной продукции на 85 % зависит от основных фондов, а на 15% от прочих факторов.
Гипотеза:
 p; остатки гомостедастичны p; остатки гомостедастичны
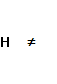 p; остатки гетероскапичны p; остатки гетероскапичны
 = = 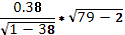 = 3,65 = 3,65
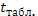 по функции = СТЬЮДРАСПОБР (0,05;79-2) = 1,99 по функции = СТЬЮДРАСПОБР (0,05;79-2) = 1,99
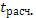 > > 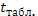 ; принимается гипотеза ; принимается гипотеза 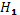 , т.е. с вероятностью 95 % остатки гетероскапичны. Дисперсия остатков каждого отклонения разная для каждого значения факторного признака. , т.е. с вероятностью 95 % остатки гетероскапичны. Дисперсия остатков каждого отклонения разная для каждого значения факторного признака.
- 2-ой тест:
Из изучаемой совокупности в 79 регионов России, убираем 7 центральных регионов. В итоге получаются 2-е группы регионов Росии, в каждой из которых по 36 регионов. Для каждой группы выводим регрессионную статистику и остатки. Остатки возводим в квадрат и с читаем сумму остатков в квадрате по каждой группе. (см. файл Excel)
Гипотеза:
 p; остатки гомостедастичны p; остатки гомостедастичны
 p; остатки гетероскапичны p; остатки гетероскапичны
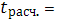 сумма Ei ^2 первой группы/ сумма Ei ^2 второй группы = 0,84 сумма Ei ^2 первой группы/ сумма Ei ^2 второй группы = 0,84
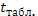 по функции =FРАСПОБР(0,05;34;34) = 1,77 по функции =FРАСПОБР(0,05;34;34) = 1,77
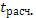 < < 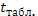 ; принимается гипотеза ; принимается гипотеза  , т.е. с вероятностью 95 % остатки гомостедастичны. Дисперсия остатков каждого отклонения одинакова для каждого значения факторного признака. , т.е. с вероятностью 95 % остатки гомостедастичны. Дисперсия остатков каждого отклонения одинакова для каждого значения факторного признака.
7. Посчитать вручную коэф-т детерминации и проверить равенство:
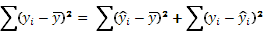
| Регионы России
|
Основные фонды в экономике (по полной учетной стоимости; на конец года), млн. руб. (Х)
|
Объём промышленной продукции, млн.руб. (
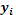 ) )
|
Расчётные значения (
 ) = ) =

|

|
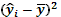
|
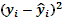
|
| Белгородская область
|
507024
|
350134
|
206998
|
1421687071
|
11115680710
|
20487970161
|
| Брянская область
|
327029
|
82119
|
163377
|
53042573657
|
22216371507
|
6602888707
|
| Владимирская область
|
328569
|
179771
|
163750
|
17598074437
|
22105255951
|
256660583,1
|
| Воронежская область
|
674657
|
169702
|
247623
|
20370920649
|
4199835275
|
6071619606
|
| Итого
|
|
|
|
2,03961E+13
|
1,74073E+13
|
2,98876E+12
|
Найдём среднее значение ( )
объёма промышленной продукции по функции =СРЗНАЧ (диапазон данных по У) = 312429 млн. руб. )
объёма промышленной продукции по функции =СРЗНАЧ (диапазон данных по У) = 312429 млн. руб.
2,03961E+13 = 1,74073E+13 + 2,98876E+12; 2,03961E+13 = 2,03961E+13 – Равенство верно.
 – коэф-т детерминации – коэф-т детерминации
 = =  = =  = 0,85% = 0,85%
8. Посчитать вручную все ошибки.
- Средняя абсолютная ошибка:  = = 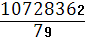 = 135802 млн. руб. = 135802 млн. руб.
- Средняя относительная ошибка: 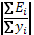 *100% = 27854 млн. руб. *100% = 27854 млн. руб.
- Средняя квадратическая ошибка:  = 197016 млн. руб. = 197016 млн. руб.
Вывод: Расчётные значения объёма промышленной продукции отличаются от фактических в среднем на 197016 млн. руб.
|