| МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
Государственный университет информатики и искусственного интеллекта
Кафедра системного анализа и моделирования
Итоговая работа
по дисциплине: «Основы дискретной математики»
на тему: «Логика формальная и графическая модель
описания изготовления винных изделий»
Выполнил:
__________ст.гр. СУА-09А А.А. Мусофранов
(дата, подпись)
Донецк 2010
План:
Введение
1. Выделение множеств
2. Отношения между множествами
3. Исследование на рефлексивность, транзитивность, симметричность
4. Построение графа
5. Матрицы смежности и инцидентности
Вывод
Список использованной литературы
Введение
Данная работа посвящена разработке логико-формальной модели описания методики изготовления винных изделий. Хотелось бы сказать пару слов о винах. По назначению вина делятся на столовые и десертные. По цвету различаются белые, розовые и красные вина. К белым относятся вина, имеющие цвет от светло-соломенного до янтарного или цвет крепко заваренного чая. У розовых и красных вин очень много оттенков от светло-рубиновых до темно-гранатовых. Белые вина с возрастом приобретают более темные тона, а красные, наоборот, бледнеют, так как красящие вещества выпадают в осадок. Эти данные необходимы для дальнейшей работы с множествами, а также для становления связи между ними( исследования на рефлексивность, транзитивность, симметричность)
Выделение множеств
Все ингредиенты и выходную продукцию можно разделить на множества.
Итак, в первом множестве будут участвовать главные ингредиенты для изготовления вина:
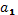 -вода; -вода;
 -этиловый спирт; -этиловый спирт;
 -сахар; -сахар;
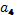 -стабилизаторы; -стабилизаторы;
 -ароматизаторы; -ароматизаторы;
 -дрожжи; -дрожжи;
 - мед; - мед;

Во втором множестве выделим разновидности винограда:
 -белый виноград; -белый виноград;
 -винный(синий); -винный(синий);
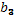 -мускатный виноград; -мускатный виноград;
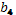 -киш-мыш; -киш-мыш;

Теперь в виде отдельного множества можно выделить разновидности исходной продукции-вина:
 -мускатное вино; -мускатное вино;
 -белое вино; -белое вино;
 -полусладкое красное вино; -полусладкое красное вино;
 -красное вино; -красное вино;
 -мадера; -мадера;

Еще раз выведем результат всех полученных множеств:



Отношение между множествами
После определения множеств можно приступить к определению взаимоотношение между ними.
Конечные множества (множество содержащее конечное количество элементов) 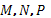 являются свойствами, которыми могут обладать или не обладать множества являются свойствами, которыми могут обладать или не обладать множества  . Итак, рассматривая правило задания множеств указанием характеристических свойств, можно определить какими свойствами будет обладать то или иное множество ,а какими нет. Это можно определить по формуле . Итак, рассматривая правило задания множеств указанием характеристических свойств, можно определить какими свойствами будет обладать то или иное множество ,а какими нет. Это можно определить по формуле
 , ,
где 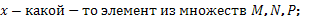 
Для получения элементов из множества С, необходимо использовать операцию объединения:


 ) )
Нужно заметить, что из полученных выше множеств нельзя построить пересечение и разность, так как исходная продукция не пересекается между собой.
Исследование на рефлективность, транзитивность, симметричность
Исследование на рефлексивность, транзитивность и симметричность производится при помощи бинарных отношений между множествами. Бинарное отношение на множество А- это всякое подмножество декартового произведения А*А. Бинарное отношение  на некоторое множество называется: на некоторое множество называется:
1) Рефлексивным, если
 ;
;
Если рассматривать данное отношение с точки зрения виноделия, то можно сделать вывод, что все элементы множества А рефлексивны по отношению к множеству С, так как полностью участвуют в его образовании.
2) Симметричность, если
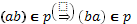 ;
;
Отношение симметричности между множествами - это возможности заменить некоторых элементов, похожих с ним по действующей силе. К таким элементам можно отнести только лишь сахар и мед, так как они могут заменять друг друга в изготовлении продукции, практически не изменяя исходный вкус вина.
3) Транзитивность, если

Транзитивность можно вычислить по соотношению: 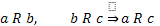 . Но по выделенным множествам явно видно, что транзитивность не один из элементов поставленных множеств не обладают, так как заменить некоторые элементы другими нельзя. . Но по выделенным множествам явно видно, что транзитивность не один из элементов поставленных множеств не обладают, так как заменить некоторые элементы другими нельзя.
Графы
Матрицы смежности и инциденции
 , ,
где А-матрица смежности;
 , ,
где В-матрица инцидентности;
Вывод
В виде вывода, хотелось бы заметить, что аппарат дискретной математики помогает в установлении соотношений между любыми выбранными элементами, а также выявляет взаимоотношения между разными множествами.
Список использованной литературы
1. http://supercook.ru/russian/rus-60.html;
2. http://ru.wikipedia.org/wiki/;
|