| ФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ
Кафедра
: «Электроснабжение железнодорожного транспорта»
Дисциплина
: «Основы теории надёжности»
Курсовая работа
«
Расчёт и анализ надёжности системы
восстанавливаемых объектов
»
Вариант-077
Выполнил:
студент гр. ЭНС-04-2
Иванов А. К.
Проверил:
канд. техн. наук, доцент
Герасимов Л. Н.
Иркутск 2008
РЕФЕРАТ
В данной курсовой работе произведён расчёт и анализ надежности технической системы без учета нагрузки.
Курсовая работа содержит:
формул 2,
таблиц 4,
рисунков 4.
Введение
Системы электроснабжения относятся к классу сложных технических систем и определяются множеством свойств, из которых к числу важнейших относится свойство надежности
технической системы.
Надежная работа устройств системы электроснабжения является необходимым условием обеспечения качественной и устойчивой работы железнодорожного транспорта. Анализ и обеспечение работоспособного состояния систем электроснабжения на этапах проектирования и эксплуатации – сложная задача, для решения которой используется математический аппарат теории надежности.
Задание на расчёт
· Определить оценки показателей надежности (коэффициент готовности) для элементов системы, показанной на схеме замещения, по данным статистки отказов и восстановления за период эксплуатации
N
лет, с учетом паспортных данных.
· Составить модель структуры сети для анализа надежности логико-вероятностным методом и определить значения ее показателей. Рассчитать и построить графики зависимости коэффициента готовности системы и вероятности отказа питания от каждого источника генерации на
L
последующих лет эксплуатации, с разбивкой по кварталам.
· Сделать выводы о необходимости технического обслуживания по критерию минимально допустимого уровня надежности.
Условия расчета
: пренебречь ненадежностью источников питания и шин 110 и 10 кв. Законы распределения отказов и восстановления принять экспоненциальными, отказы элементов - независимыми. Для двухцепных ЛЭП учитывать только отказ 2-х цепей. Для трансформаторов учитывать только восстановление аварийным ремонтом.
Принять в данной задаче, что пропускная способность всех устройств сети выше максимальной нагрузки.
ИСХОДНЫЕ ДАННЫЕ
Схема замещения заданной подстанции показана на рис 1, ее описание и исходные данные приведены в табл. 1.
Описание схемы и параметры расчета:
· Длина линий: Л1
= 42 км; Л2
= 142 км. Линия Л2
– двухцепная.
· Выключатели: В1
и В2
- масляные, В3
– воздушный.
· Период эксплуатации N = 6 лет; период прогнозирования L = 3 года.
· Минимально допустимый уровень надежности kГдоп
= 0.89 .
Все выключатели и отделители включены.
Таблица 1
Исходные данные по элементам схемы
| Элемент
|
λ – частота
отказов,
откл/год
|
t
в
- ср. время восстановления,
10-3
лет/отказ
|
Число
отказов
|
Время
восстановления
10-3
лет/отказ
|
| Паспортные данные
|
Статистика отказов
|
| В1
|
0.01
|
2.5
|
2
|
26.8; 12.6
|
| В2
|
0.01
|
2.5
|
3
|
31.5; 17.6; 23.7
|
| В3
|
0.07
|
2.5
|
0
|
-
|
| В4
|
0.01
|
2.5
|
2
|
18.6; 42.2
|
| Л1
|
0.592
|
0.5
|
1
|
16.4
|
| Л2
|
0.625
|
3.0
|
0
|
-
|
| От1
|
0.013
|
0.4
|
0
|
-
|
| От2
|
0.013
|
0.4
|
0
|
-
|
| От3
|
0.013
|
0.4
|
0
|
-
|
| Т1
|
0.01
|
60.0
|
0
|
-
|
| Т2
|
0.01
|
60.0
|
0
|
-
|
| Т3
|
0.01
|
60.0
|
0
|
-
|
Решение
Жирным шрифтом (табл. 1) выделены параметры линий, пересчитанные на их конкретную длину:
| Л1
:
|
1.41·(42 км/100 км) = 0.592 откл/год;
|
| Л2
:
|
0.44·(142 км/100 км) = 0.625 откл/год.
|
По данным статистики отказов, рассчитаем оценки частоты отказов и среднего времени их восстановления.
| g = N /M ;
λ
i
*
= (1-g) ·
λ
i
+ g ·(ni
\N);
t
в
i
*
= (1-g) · t
в
i
+ g ·
(  );
);
|
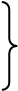
|
(1)
|
где N -
период эксплуатации; M=
N+15
– полное «время старения» априорных данных;
i
– номер элемента, ni
– число отказов i-го
элемента за период эксплуатации; j
- индекс; 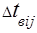 - время восстановления i-го
элемента при j
-м отказе. Верхним индексом * отмечены оценки параметров – эти значения должны быть использованы в формуле коэффициентов готовности элементов. - время восстановления i-го
элемента при j
-м отказе. Верхним индексом * отмечены оценки параметров – эти значения должны быть использованы в формуле коэффициентов готовности элементов.
kг
= . (2) . (2)
Приведем пример расчета для одного из отказавших элементов (выключатель В1
):
· вес измерений определим как «коэффициент старения информации»:
g
= 6/(6+15) = 0.28; (1-
g
) = 0.72;
· оценки параметров найдем по формулам (1.4) и (1.3):
λ*( В1
) = (1-
g
) · λ( В1
) +
g
· ( 2/6 ) =
= 0.72∙0.01 + 0.28∙0.33 = 0.1005 откл/год;
t
*в
(В1
) = (1-
g
) ·
t
в
( В1
) +
g
· [(26.8+ 12.6)/2] =
= 0.72 ∙2.5 + 0.28 ∙19.7 = 7.316 ·10-3
лет/отказ.
k
г
(В1
)
= 1 / (1+ 0,1005∙7.316∙10-3
) = 0.99926
В табл. 2 приведены результаты расчетов. При отсутствии данных об отказах, остаются паспортные (априорные) значения. В таблицу введен дополнительный столбец «переменная xi
», который будет заполнен далее.
Таблица 2
Результаты расчета показателей по статистике отказов
| Элемент
|
Переменная
xi
|
λ* – частота
отказов,
откл/год
|
t
*в
- ср. время
восстановления
10-3
лет/отказ
|
Кг
-коэфф.
готовности
|
| В1
|
x
1
|
0,1005
|
7,316
|
0,99926
|
| В2
|
X
5
|
0,1472
|
8,594
|
0,99873
|
| В3
|
x
23
|
0,07
|
2,5
|
0,99982
|
| В4
|
x34
|
0,1005
|
10,312
|
0,99896
|
| Л1
|
x
1
2
|
0,4729
|
4,952
|
0,99766
|
| Л2
|
x45
|
0,625
|
3
|
0,999
|
| От1
|
x
2
6
|
0,013
|
0,4
|
0,99999
|
| От2
|
x
3
7
|
0,013
|
0,4
|
0,99999
|
| От3
|
x48
|
0,013
|
0,4
|
0,99999
|
| Т1
|
x6
|
0,01
|
60,0
|
0,9994
|
| Т2
|
x7
|
0,01
|
60,0
|
0,9994
|
| Т3
|
x8
|
0,01
|
60,0
|
0,9994
|
Исходя из заданной схемы замещения, составим ЛФР, учитывая все возможные пути от источника к потребителю. Для этого преобразуем исходную схему к структурной для анализа надежности, введя дополнительные узлы и переменные состояния
xi
.
Отметим, что понятия «узлы» и «связи» для схем замещения и структурной могут не совпадать: так, отделитель «От1
» представлен в структурной схеме «связью» x
26
, см. рис 2. Кроме того, так как объекты генерации и шины 10 кв., по условию задачи, абсолютно надежны, при составлении схемы для анализа надежности их можно не учитывать, если они не являются элементами связи или ветвления (например – шины 110 кв должны быть введены в структурную схему как узлы ветвления 2 и 3).
Переменные структурной схемы описаны в таблице соответствия 3.
Таблица 3
Соответствие параметров состояния структурной схемы элементам схемы замещения
| x
1
: состояние выключателя В1
,
|
х5
: состояние выключателя В2
,
|
| x
12
: состояние линии Л1
,
|
x
26
: состояние отделителя От1
,
|
| x
2
: состояние шин 110 кв ,
|
х6
: состояние трансформатора Т 1 ,
|
| x
23
: состояние выключателя ШСВ В3
|
х
37
: состояние отделителя От2
,
|
| x
3
: состояние шин 110 кв ,
|
х7
: состояние трансформатора Т2
,
|
| x
34
: состояние выключателя ШСВ В4
|
х
48
: состояние отделителя От3
,
|
| х4
: состояние шин 110 кв,
|
х8
: состояние трансформатора Т3
.
|
| x
45
: состояние линии Л2
,
|
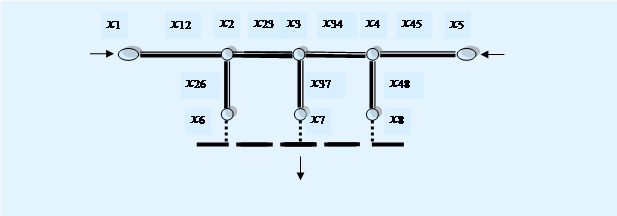
Рис 2. Структурная схема анализа надёжности
Из схемы на рис 2 видно, что ЛФР системы представляет дизъюнкцию ЛФР шести путей электропитания (в индексе пути использованы только номера узлов структурной схемы):
Z =
Z1-2-6
+
Z1-2-3-7
+
Z1-2-3-4-8
+
Z5-4-8
+
Z5-4-3-7
+
Z5-4-3-2-6 .
Раскрывая ЛФР правой части, получим
Z
= (
x
1
x
12
x
2
x
26
x
6
)+(
x
1
x
12
x
2
x
23
x
3
x
37
x
7
)+ (
x
1
x
12
x
2
x
23
x
3
x
34
x
4
х48
х8
)+ +(
x
5
x
45
x
4
x
48
x
8
)+(
x
5
x
45
x
4
x
34
x
3
x
37
x
7
)+ (
x
5
x
45
x
4
x
34
x
3
x
23
x
2
х26
х6
).
Упростим данное выражение, учитывая, что x
2
=1,
x
3
=1 и х4
=1,
Z
= (
x
1
x
12
)·(
x
26
x
6
+
x
23
·(
x
37
x
7
+ х34
х48
х8
))+ (
x
5
x
45
)·(
x
48
x
8
+
x
34
·(
x
37
x
7
+ +х23
х26
х6
)) =
Z
1-2
· (
Z
2-6
+
Z
2-3
(
Z
3-7
+
Z
3-8
)) +
Z
5-4
·(
Z
4-8
+
Z
4-3
(
Z
3-7
+
Z
3-6
))
Структурная схема представления ЛФР показана на рис. 3.
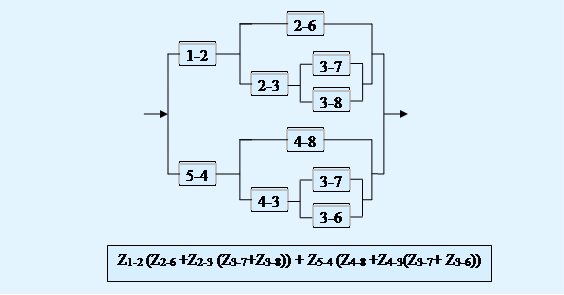
Рис 3. Схема представления ЛФР
Раскроем выражения составляющих ЛФР P(
Z = 1),
для ее конкретного представления и заданного экспоненциального закона распределения:
· Для блоков последовательных элементов на рис. 3:
P(Z1-2
=1 ) = P(x1
=1)·P( x12
=1) = p1-2
= 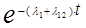 , ,
P(Z5-4
=1 ) = P(x5
=1)·P( x45
=1) = p5-4
=
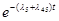 , ,
P(Z2-3
=1 ) = P(x23
=1) = p2-3
=
 , ,
P(Z4-3
=1 ) = P(x43
=1) = p4-3
=
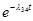 . .
· Для блоков параллельных элементов на рис. 3:
P
(
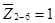 ) =
P
( ) =
P
(
 26
=1)·
P
(
26
=1)·
P
(
 6
=1) =
q
2-6
=
6
=1) =
q
2-6
=
 , ,
P
(
 ) =
P
( ) =
P
(
 37
=1)·
P
(
37
=1)·
P
(
 7
=1) =
q
3-7
=
7
=1) =
q
3-7
=
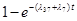 , ,
P
(
 ) =
P
( ) =
P
(
 34
=1)·
P
(
34
=1)·
P
(
 48
=1)·
P
(
48
=1)·
P
(
 8
=1) =
q
3-8
=
8
=1) =
q
3-8
=
 , ,
P
(
 ) =
P
( ) =
P
(
 48
=1)·
P
(
48
=1)·
P
(
 8
=1) =
q
4-8
=
8
=1) =
q
4-8
=
 , ,
P
(
 ) =
P
( ) =
P
(
 23
=1)·
P
(
23
=1)·
P
(
 26
=1)·
P
(
26
=1)·
P
(
 6
=1) =
q
3-6
=
6
=1) =
q
3-6
=
 , ,
Введем промежуточные обозначения:
p
3-7-8
= 1-
q
3-7-8
= 1-
q
3-7
∙
q
3-8
-
ВБР блока параллельных элементов Z
3-7
+
Z
3-8
,
p
3-7-6
= 1-
q
3-7-6
= 1-
q
3-7
∙
q
3-6
-
ВБР блока параллельных элементов Z
3-7
+
Z
3-6
,
q
2-7-8
= 1-
p
2-7-8
= 1-
p
2-3
∙
p
3-7-8
-
вероятность отказа блока последовательных элементов Z
2-3
(
Z
3-7
+
Z
3-8
) ,
q
4-7-6
= 1-
p
4-7-6
= 1-
p
4-3
∙
p
3-7-6
–
вероятность отказа блока последовательных элементов Z
4-3
(
Z
3-7
+
Z
3-6
),
p
2-6-7-8
= 1-
q
2-6-7-8
= 1-
q
2-6
∙
q
2-7-8
–
ВБР питания на пути от узла №2 на схеме замещения,
p
4-8-7-6
= 1-
q
4-8-7-6
= 1-
q
4-8
∙
q
4-7-6
-
ВБР питания на пути от узла №4 на схеме замещения,
q
1*
= 1 -
p
1-2
∙
p
2-6-7-8
-
ВО питания на пути от узла №1 на схеме замещения,
q
5*
= 1 –
p
5-4
∙
p
4-8-7-6
-
ВО питания на пути от узла №2 на схеме замещения.
В итоге, записываем окончательно
Q =
q1*
∙
q5*
;
kГ
(
t) =
P(
Z = 1) = 1 –
Q.
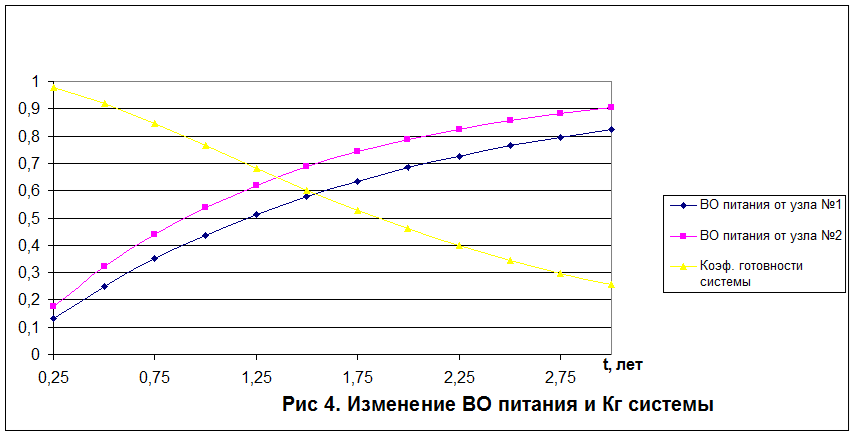
Расчеты, выполненные по полученным формулам, приведены в табл. 4. Данные таблицы характеризуют изменение составляющих ЛФР на заданном периоде предстоящей эксплуатации (L = 3 года) с поквартальной разбивкой. На рис. 4. показаны графики изменения трех основных показателей надежности данной системы: q
1*
∙(
t
),
q
5*
(
t
) ,
k
Г
(
t
),
построенные по данным табл. 1.4. Такой вид изменения показателей во времени типичен для экспоненциального закона распределения.
На основании полученных результатов следует провести качественный анализ надежности заданной схемы электропитания и сделать выводы о необходимости технического обслуживания на рассматриваемом периоде эксплуатации.
Точное значение tдоп
может быть получено решением уравнения
kГ
(tдоп
) = kГдоп
,
любым из численных методов, но для планирования сроков технического обслуживания достаточно указать интервал времени, в котором первый раз нарушается критерий, так как зависимость kГ
(tдоп
)
является монотонно убывающей.
Из таблицы и графиков видно, что критерий нарушается уже в третьем квартале 1-го года последующей эксплуатации:
kГ
(
0.5) > kГдоп
> kГ
(
0.75),
или: 0.9199 > 0.9 > 0.8458,
поэтому tдоп
= 0.5 и техническое обслуживание (профилактическое) следует назначить во втором квартале.
Таблица 4
| Формула
Z(*)
|
Σλ
|
1-й год
|
2-й год
|
3-й год
|
| 0,25
|
0,5
|
0,75
|
1
|
1,25
|
1,5
|
1,75
|
2
|
2,25
|
2,5
|
2,75
|
3
|
| p12
=
|
0,57344
|
0,866442
|
0,750722
|
0,650457
|
0,563583
|
0,488312
|
0,423094
|
0,366587
|
0,317626
|
0,275205
|
0,238449
|
0,206602
|
0,179009
|
| p5-4
=
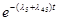
|
0,7722
|
0,824441
|
0,679703
|
0,560374
|
0,461996
|
0,380888
|
0,31402
|
0,258891
|
0,21344
|
0,175969
|
0,145076
|
0,119606
|
0,098608
|
| p2-3
=
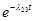
|
0,07
|
0,982652
|
0,965605
|
0,948854
|
0,932394
|
0,916219
|
0,900325
|
0,884706
|
0,869358
|
0,854277
|
0,839457
|
0,824894
|
0,810584
|
| p4-3
=
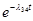
|
0,10053
|
0,97518
|
0,950976
|
0,927372
|
0,904355
|
0,881909
|
0,86002
|
0,838674
|
0,817858
|
0,797559
|
0,777763
|
0,758459
|
0,739634
|
| q
2-6
=
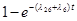
|
0,023
|
0,005734
|
0,011434
|
0,017102
|
0,022738
|
0,028341
|
0,033912
|
0,039451
|
0,044958
|
0,050434
|
0,055878
|
0,061291
|
0,066673
|
| q
3-7
=
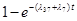
|
0,023
|
0,005734
|
0,011434
|
0,017102
|
0,022738
|
0,028341
|
0,033912
|
0,039451
|
0,044958
|
0,050434
|
0,055878
|
0,061291
|
0,066673
|
| q
3-8
=

|
0,12353
|
0,030411
|
0,059898
|
0,088488
|
0,116208
|
0,143085
|
0,169145
|
0,194412
|
0,218911
|
0,242665
|
0,265697
|
0,288028
|
0,30968
|
| q
4-8
=

|
0,023
|
0,005734
|
0,011434
|
0,017102
|
0,022738
|
0,028341
|
0,033912
|
0,039451
|
0,044958
|
0,050434
|
0,055878
|
0,061291
|
0,066673
|
| q
3-6
=
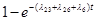
|
0,093
|
0,022982
|
0,045435
|
0,067373
|
0,088806
|
0,109747
|
0,130207
|
0,150196
|
0,169726
|
0,188808
|
0,20745
|
0,225664
|
0,24346
|
| p
3-7-8
=1-
q
3-7
∙
q
3-8
|
-
|
0,999826
|
0,999315
|
0,998487
|
0,997358
|
0,995945
|
0,994264
|
0,99233
|
0,990158
|
0,987761
|
0,985153
|
0,982346
|
0,979353
|
| p
3-7-6
= 1-
q
3-7
∙
q
3-6
|
-
|
0,999868
|
0,99948
|
0,998848
|
0,997981
|
0,99689
|
0,995584
|
0,994075
|
0,992369
|
0,990478
|
0,988408
|
0,986169
|
0,983768
|
| q
2-7-8
=1-
p
2-3
∙
p
3-7-8
|
-
|
0,017519
|
0,035056
|
0,052582
|
0,07007
|
0,087497
|
0,10484
|
0,12208
|
0,139198
|
0,156178
|
0,173006
|
0,189668
|
0,206152
|
| q
4-7-6
=1-
p
4-3
∙
p
3-7-6
|
-
|
0,024949
|
0,049518
|
0,073696
|
0,097471
|
0,120834
|
0,143778
|
0,166296
|
0,188383
|
0,210036
|
0,231253
|
0,252032
|
0,272372
|
| p
2-6-7-8
=1-
q
2-6
∙
q
2-7-8
|
-
|
0,9999
|
0,999599
|
0,999101
|
0,998407
|
0,99752
|
0,996445
|
0,995184
|
0,993742
|
0,992123
|
0,990333
|
0,988375
|
0,986255
|
| p
4-8-7-6
=1-
q
4-8
∙
q
4-7-6
|
-
|
0,999857
|
0,999434
|
0,99874
|
0,997784
|
0,996575
|
0,995124
|
0,99344
|
0,991531
|
0,989407
|
0,987078
|
0,984553
|
0,98184
|
| q
1*
= 1 -
p
1-2
∙
p
2-6-7-8
|
-
|
0,133645
|
0,249579
|
0,350128
|
0,437315
|
0,512899
|
0,57841
|
0,635179
|
0,684362
|
0,726963
|
0,763856
|
0,7958
|
0,823452
|
| q
5*
= 1 –
p
5-4
∙
p
4-8-7-6
|
-
|
0,175677
|
0,320682
|
0,440332
|
0,539028
|
0,620416
|
0,687512
|
0,742808
|
0,788368
|
0,825895
|
0,856799
|
0,882241
|
0,903182
|
| k
Г
(
t
)=1 –
q1*
q5*
|
-
|
0,976522
|
0,919964
|
0,845828
|
0,764275
|
0,681789
|
0,602337
|
0,528184
|
0,460471
|
0,399605
|
0,345529
|
0,297913
|
0,256273
|
Заключение
В курсовой работе были показаны методы исследования и обеспечения надежности технических систем и получение практических навыков в определении отдельных показателей надежности применительно к устройствам электроснабжения. Нами рассматривался логико-вероятностный метод построения модели сложной системы для расчета и анализа надежности заданного объекта электроснабжения.
Литература
1. Надежность и диагностика систем электроснабжения железных дорог: учебник для ВУЗов ж\д транспорта / А.В. Ефимов, А.Г. Галкин.- М: УМК МПС России, 2000. - 512с.
2. Китушин В.Г. Надежность энергетических систем: учебное пособие для электроэнергетических специальностей вузов.- М.: Высшая школа, 1984. – 256с.
3. Ковалев Г.Ф. Надежность и диагностика технических систем: задание на контрольную работу №2 с методическими указаниями для студентов IV курса специальности «Электроснабжение железнодорожного транспорта». – Иркутск: ИРИИТ, СЭИ СО РАН, 2000. -15с.
4. Дубицкий М.А. Надежность систем энергоснабжения: методическая разработка с заданием на контрольную работу. – Иркутск: ИрИИТ, ИПИ, СЭИ СО РАН, 1990. -34с.
5. Пышкин А.А. Надежность систем электроснабжения электрических железных дорог. – Екатеринбург: УЭМИИТ, 1993. - 120 с.
6. Шаманов В.И. Надежность систем железнодорожной автоматики и телемеханики: учебное пособие. Иркутск: ИрИИТ, 1999. 223с.
7. Гук Ю.Б. Анализ надежности электроэнергетических установок. - Л.: Энергоатомиздат, Ленинградское отд., 1988. – 224с.
8. Маквардт Г.Г. Применение теории вероятностей и вычислительной техники в системе энергоснабжения.- М.: Транспорт, 1972. - 224с.
9. Надежность систем энергетики. Терминология: сборник рекомендуемых терминов. - М.: Наука, 1964. -Вып. 95. – 44с.
|