
ОТЧЕТ
Лабораторная работа по курсу "Общая физика"
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДЫХ ТЕЛ
Работу выполнил студент группы 0ОП5а Кузнецов Д.А.
1. ЦЕЛЬ РАБОТЫ
Целью настоящей работы является определение момента инерции твердых тел и экспериментальная проверка справедливости теоремы Штейнера на примере физического маятника.
2. ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКИ ЭКСПЕРИМЕНТА
Для экспериментальной проверки теоремы Штейнера и определения момента инерции в данной работе используется стандартная установка универсального маятника ФПМО - 4. Это настольный прибор (рис. 4.1), на вертикальной стойке основания 1 которого крепится кронштейн 2, который имеет возможность поворота вокруг стойки на 360° и фиксация в любом выбранном положении. С одной стороны кронштейна 2 подвешен математический маятник, а с другой - физический. Математический маятник представляет собой металлический шарик 3 на бифилярном подвесе 4. Физический маятник - стальной стержень 5, подвешенный на опорной призме 6. Опорная призма 6 может перемещаться по всей длине стержня и фиксироваться в требуемом положении.Стержень 5 имеет кольцевые проточки, которые служат для надежной фиксации опорных призм. Установка снабжена фотоэлектрическим датчиком 7, который закреплен на вертикальной стойке с помощью кронштейна 8 и имеет возможность перемещаться как вдоль, так и вокруг стойки и фиксироваться в любом положении. Датчик предназначен для выдачи сигналов на миллисекундомер 9. Миллисекундомер физический выполнен самостоятельным прибором с цифровой индикацией времени и количества полных периодов колебаний маятника.
3. ОСНОВНЫЕ РАСЧЕТНЫЕ ФОРМУЛЫ
Средняя величина периода колебаний маятника:
T
= t
/ n
, (3.1)
где t
- продолжительность 10 - 15 колебаний;
n
- число колебаний за время t
.
Формула для экспериментального расчета момента инерции прямого тонкого стержня
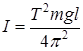 , (3.2) , (3.2)
где T
- период колебаний маятника;
l
- расстояние от центра масс до точки подвеса маятника;
m
- масса маятника;
g
- ускорение свободного падения.
Формула для теоретического расчета момента инерции прямого тонкого стержня длиной d
и массой m
относительно оси, перпендикулярной к стержню и проходящей через его середину:
I0
=
md
2
/12
(3.3)
4. РЕЗУЛЬТАТЫ РАБОТЫ И ИХ АНАЛИЗ.
Результаты прямых и косвенных измерений представлены в таблице.
Таблица.
Данные измерений
| Номер опыта |
n
|
t
, c |
T
, c |
l2
,
м2
|
I,
кг×м2
|
Примечание |
| 1 |
10 |
12,591 |
1,2591 |
0,03829 |
m
= 358 г
s(t
) = ± 2 мс
d(m
) = 2%
|
| 2 |
10 |
12,280 |
1,2280 |
0,03107 |
| 3 |
10 |
12,095 |
1,2095 |
| 4 |
10 |
12,155 |
1,2155 |
| 5 |
10 |
12,781 |
1,2781 |
| 6 |
10 |
14,658 |
1,4658 |
| 7 |
10 |
21,096 |
2,1096 |
Подсчитаем среднюю величину периода колебаний маятника (3.1)
T1
=12,591/ 10 = 1,2591
T2
=12,280/ 10 = 1,2280
T3
=12,095/ 10 = 1,2095
T4
=12,155/ 10 = 1,2155
T5
=12,781/ 10 = 1,2781
T6
=14,658/ 10 = 1,4658
T7
=21,096/ 10 = 2,1096
Теперь найдем момент инерции прямого тонкого стержня по формуле (3.2)
(1,25)2
* 0,358 * 10 *0,27
 I1
= = 0,03829 I1
= = 0,03829
4 * (3,14)2
(1,22)2
* 0,358 * 10 * 0,23
 I2
= = 0,03107 I2
= = 0,03107
4 * (3,14)2
I3
= 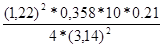 ≈ 0,02837 ≈ 0,02837
I4
= 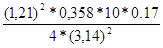 ≈ 0,02259 ≈ 0,02259
I5
= 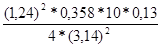 ≈ 0,01814 ≈ 0,01814
I6
= 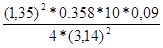 ≈ 0,01489 ≈ 0,01489
I7
= 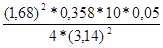 ≈ 0,01281 ≈ 0,01281
Абсолютная погрешность замера времени колебаний составляет ± 2 мс, а с учётом вычисления периода ± 2×10-4
, то вычисляем результаты с точностью до пяти знаков.
Расчёт случайной погрешности измерения для построения графика
t1
= < t1
>  σ (t) = 12,785 σ (t) = 12,785  0,02 0,02
t2
= < t2
>  σ (t) = 12,404 σ (t) = 12,404  0,02 0,02
t3
= < t3
>  σ (t) = 12,156 σ (t) = 12,156  0,02 0,02
t4
= < t4
>  σ (t) = 12,092 σ (t) = 12,092  0,02 0,02
t5
= < t5
>  σ (t) = 12,404 σ (t) = 12,404  0,02 0,02
t6
= < t6
>  σ (t) = 13,473 σ (t) = 13,473  0,02 0,02
t7
= < t7
>  σ (t) = 16,752 σ (t) = 16,752  0,02 0,02
От абсолютной погрешности замера времени колебаний зависит момент инерции прямого тонкого стержня, а расстояние от масс до точки подвеса маятника не зависит.
T1
= < T1
>  σ (t) / n = σ (t) / n =
T2
= < T2
>  σ (t) / n = 1,2404 σ (t) / n = 1,2404 0,002 0,002
T3
= < T3
>  σ (t) / n = 1,2156 σ (t) / n = 1,2156 0,002 0,002
T4
= < T4
>  σ (t) / n = 1,2092 σ (t) / n = 1,2092 0,002 0,002
T5
= < T5
>  σ (t) / n = 1,2404 σ (t) / n = 1,2404 0,002 0,002
T6
= < T6
>  σ (t) / n = 1,3473 σ (t) / n = 1,3473 0,002 0,002
T7
= < T7
>  σ (t) / n = 1,6752 σ (t) / n = 1,6752 0,002 0,002
I1 max
= 0,04315 I1 min
= 0,04311
I2 max
= 0,03491 I2
min
= 0,03487
I3 max
= 0,02839 I3 min
= 0,02835
I4 max
= 0,02261 I4 min
= 0,02257
I5 max
= 0,01816 I5 min
= 0,01812
I6 max
= 0,01491 I6 min
= 0,01487
I7 max
= 0,01283 I7
min
= 0,01279

5. ВЫВОДЫ:
В результате проделанной работы мы убедились в справедливости теоремы Штейнера I = I0
+ml2
, так как смогли в пределах погрешностей измерений построить линеаризованный график зависимости I и l2
.
6. Контрольные вопросы.
6.1. Моментом инерции материальной точки относительно неподвижной оси вращения называется физическая величина I, равная произведению массы m материальной точки на квадрат расстояния r² до оси:
I = m r²
Момент инерции твёрдого тела относительно неподвижной оси вращения, складывается из моментов инерции отдельных его материальных точек:
I =Σ mi ri².
6.2. Если известен момент инерции тела относительно, какой – либо оси, проходящей через центр масс.
6.3. Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела и произведения массы тела m на квадрат расстояния l между осями:
I = I0 + m l².
6.4. Под действием составляющей силы тяжести P1 = Psinφ .
6.5. Является.
6.6. Зная ускорение свободного падения g, массу m, экспериментально измерив l и определив T, тогда можно вычислить момент инерции.
6.7. Физическим маятником называется любое твёрдое тело, которое под действием силы тяжести может свободно качаться вокруг неподвижной оси, не проходящей через центр масс.
6.8. Для малых углов отклонения.
|