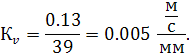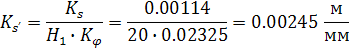Курсовая работа: Структурный анализ рычажного механизма
|
Название: Структурный анализ рычажного механизма Раздел: Промышленность, производство Тип: курсовая работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Федеральное агенство по образованию ГОУ ВПО «Уральский государственный технологический университет – УПИ» Нижнетагильский технологический институт (филиал) УГТУ-УПИ пояснительная запискаПЗ.1501.00.00.03(2) к курсовому проекту по теории механизмов и механике машин Нижний Тагил 2008 СОДЕРЖАНИЕ 1. Структурный анализ рычажного механизма 1.1. Схема рычажного механизма. 1.2. Классификация кинематических пар 1.3. Определение степени подвижности механизма 1.4. Определение класса и порядка механизма по Ассуру 2.1. Определение геометрических размеров механизма. 2.2. Построение плана положений механизма. 2.5. Построение графиков аналога скорости и ускорения механизма. 3. Силовой расчёт рычажного механизма 3.1. Определение силы полезного сопротивления 3.2. Определение сил тяжести звеньев. 3.3. Определение сил инерции и моментов сил инерции звеньев. 3.6. Расчёт группы начального звена. 4. Проектирование эвольвентных профилей зубчатых колес 5. Синтез кулачкового механизма. Список использованных источников
1.1. Схема рычажного механизма.
Схема рычажного механизма (механизма поперечно-строгального станка) приведена на рис. 1.
Механизм состоит из шести звеньев: 0-стойка, неподвижное звено; 1-кривошип, подвижное звено, совершает вращательное движение; 2-ползун кулисы, совершает поступательное движение; 3-кулиса, совершает вращательное движение; 4-ползун, совершает поступательное движение; 5-ползун, совершает поступательное движение. 1.2. Классификация кинематических пар Кинематической парой называется подвижное соединение двух звеньев, ограничивающее их относительное движение. Кинематические пары механизма компрессора показаны на рис. 2. Таблица 1. Классификация кинематических пар
По характеру соприкосновения элементов звеньев кинематические пары являются низшими . По характеру относительного движения звеньев кинематические пары являются плоскими . По числу условий связи, наложенных на относительное движение звеньев, кинематические пары являются парами5-го класса . По характеру замыкания элементов звеньев кинематические пары являются парами с геометрическим замыканием . 1.3. Определение степени подвижности механизма.Степень подвижности плоского механизма определяется по формуле П.Л.Чебышева
где
Подставляя значения параметров в формулу Чебышева, получим
Число W показывает, скольким звеньям необходимо задать закон движения для получения определенности движения всего механизма. Звено, закон движения которого задан, называется начальным звеном . В рассматриваемом механизме начальным звеном является кривошип ОА. 1.4. Определение класса и порядка механизма по Ассуру.Так как степень подвижности механизма равна единице, то группа начального звена состоит из одного подвижного звена 1 и стойки. Такая группа по классификации Ассура относится к 1-му классу, 1-му порядку. С группой начального звена соединена группа Ассура 2-3, состоящая из ползуна 2, кулисы 3. Эта группа относится к 2-му классу, 3-му порядку. С группой Ассура 2-3 соединена группа Ассура 3-4, состоящая из кулисы 3, и ползуна, которая также относится к 2-му классу, 2-му порядку. С группой Ассура 3-4 соединена группа Ассура 4-5, состоящая из стойки и ползуна 5, которая относится к 2-му классу, 2-му порядку. Класс и порядок механизма определяется классом и порядком наиболее сложной группы, входящей в его состав. Следовательно, данный механизм 2-го класса, 2-го порядка. Вывод . Механизм может существовать и для его работы необходимо и достаточно иметь один двигатель. 2.Синтез механизма 2.1. Определение геометрических размеров звеньев механизма.
Угол перекрытия по формуле [2.17(1)]:
где
Угол качания кулисы [стр. 64(1)]:
Длина кулисы [стр. 64(1)]:
где H=0.45 м-ход ползуна.
Высота сигмента [стр. 64(1)]:
Расстояние между опорой кривошипа и осью ползуна 5 [стр. 64(1)]:
где
Длина кривошипа [стр. 64(1)]:
2.2. Построение плана положений механизма.Масштабный коэффициент длин – это отношение истинной длины кривошипа l 1 к длине отрезка в мм, изображающего его на чертеже. Приняв графическое значение длины кривошипа l OA = 53.01 мм, найдем значение Kl :
Графические значения линейных размеров находятся как отношения истинных значений к значению масштабного коэффициента длин Kl :
Имея графические значения линейных размеров (длин звеньев и расстояний между опорами), строим план 12 положений механизма из одной общей точки О вращения кривошипа ОА, начиная с разбивки траектории движения точки А конца кривошипа на 12 равных частей. Методом засечек находятся положения всех звеньев механизма для каждого из 12 положений кривошипа. План положений механизма показан на листе 1 чертежей курсовой работы. Построение графика перемещения исполнительного звена. Измерением находим перемещение точки B относительно начального положения механизма (точка 1) с учетом масштабного коэффициента:
Выберем масштабный коэффициент графика перемещения:
Рассчитаем координаты точек по оси ординаты.
Найдём масштабные коэффициенты по оси абцисс. Масштабный коэффициент угла поворота кривошипа:
где L =240 мм-длина по оси абцисс.
Масштабный коэффициент времени поворота кривошипа:
где n =94 об/мин-частота вращения кривошипа.
2.3. Построение плана скоростей механизма.2.3.1. Положение кривошипа 1. Угловая скорость вращения кривошипа определяется по формуле
Линейная скорость точки А кривошипа равна
Масштабный коэффициент скорости KV
определяется как отношение истинного значения скорости точки А
кривошипа к длине отрезка в мм, изображающего эту скорость на чертеже. Приняв графическое значение скорости
Строим вектор Для определения скорости точки A 3 , принадлежащей кулисе, составим векторные уравнения
где
где
Пересечение векторов
Строим вектор Находим значение скорости точки А3
Для определения скорости точки В составим векторное уравнение
где
Угловая скорость кулисы равна
где
Следовательно,
Скорость центра тяжести кулисы S3
где
Для определения скорости центра тяжести S 5 , принадлежащей ползуну 5, составим векторное уравнение
где
Пересечение этих векторов образуют точку
2.3.2. Положение кривошипа 2. Аналогично находим скорости для остальных положений механизма. Угловая скорость вращения кривошипа определяется по формуле
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3.3. Положение кривошипа 3.
Строим вектор
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 4 . Положение кривошипа 4 .
Строим вектор
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 5 . Положение кривошипа 5 .
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 6 . Положение кривошипа 6 .
Строим вектор
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 7 . Положение кривошипа 7 .
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 8 . Положение кривошипа 8 .
Строим вектор
где
где
Пересечение векторов
Строим вектор
где
Угловая скорость кулисы равна
где
Следовательно, Скорость центра тяжести кулисы S3
где
Для определения скорости центра тяжести S 5 , принадлежащей ползуну 5, составим векторное уравнение
где
Пересечение этих векторов образуют точку
2.3. 9 . Положение кривошипа 9 .
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 10 . Положение кривошипа 10 .
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 11 . Положение кривошипа 11 .
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.3. 12 . Положение кривошипа 12 .
Строим вектор
где
где
Пересечение векторов
где
Угловая скорость кулисы равна
Скорость центра тяжести кулисы S3
где
Пересечение этих векторов образуют точку
2.4. Построение плана ускорений механизма. Определение ускорений шарнирных точек, центров тяжести звеньев и угловых ускорений звеньев. Ускорение находим для трех заданных положений кривошипа 3, 7, 10. Ускорение точки А одинаково для всех положений кривошипа и равно
Т. к. движение кривошипа равномерное, по окружности, то тангенциальное ускорение
Нормальное ускорение
где
Выбираем масштабный коэффициент. Принимаем
2.4.1. Ускорений шарнирных точек, центров тяжести звеньев и угловых ускорений звеньев для положения кривошипа 3. Ускорение точки А 3
где ускорение Кориолиса равно
направление
Ускорение точки А 3 относительно точки С
где
Длина векторов на плане ускорений:
Измерением находим Ускорение точки А 3
Угловое ускорение кулисы
где АС= 459.26 мм;
Ускорение точки B
Ускорение центра тяжести кулисы S3
Длина векторов на плане ускорений:
Ускорение центра тяжести ползуна B5
где
Пересечение этих векторов образуют точку b 5 на плане ускорений.
2.4.2. Ускорений шарнирных точек, центров тяжести звеньев и угловых ускорений звеньев для положения кривошипа 7. Ускорение точки А 3
Ускорение точки А 3 относительно точки С
Длина векторов на плане ускорений:
Измерением находим Ускорение точки А 3
Угловое ускорение кулисы
где АС= 422.81 мм;
Ускорение точки B
Ускорение центра тяжести кулисы S3
Длина векторов на плане ускорений:
Ускорение центра тяжести ползуна B5
где
Пересечение этих векторов образуют точку b 5 на плане ускорений.
2.4.3. Ускорений шарнирных точек, центров тяжести звеньев и угловых ускорений звеньев для положения кривошипа 10. Ускорение точки А 3
Ускорение точки А 3 относительно точки С
Длина векторов на плане ускорений:
Измерением находим Ускорение точки А 3
Угловое ускорение кулисы
где АС= 138.95 мм;
Ускорение точки B
Ускорение центра тяжести кулисы S3
Длина векторов на плане ускорений:
Ускорение центра тяжести ползуна B5
где
Пересечение этих векторов образуют точку b 5 на плане ускорений.
2.5. Построение графиков аналога скорости и ускорения механизма Найдём дополнительные значения масштабов, необходимые для верного построения диаграмм:
где Строим график аналога скорости методом дифференцирования графика перемещения, а аналога ускорения дифференцированием графика аналога скорости. 3. Силовой расчёт рычажного механизма 3.1. Определение силы полезного сопротивления.Сила полезного сопротивления, действующая на ползун, определяется согласно заданного графика технологической нагрузки (лист 2).
3.2. Определение массы звеньев.Массы звеньев (кг), определяемые как отношение веса к ускорению свободного падения, равны:
Так как силы тяжести звеньев 2,4 малы по сравнению с технологической нагрузкой условно принимаем их массы равными нулю. 3.3. Определение сил инерции и моментов сил инерции звеньев.Силы инерции звеньев (Н), определяемые как произведение массы на ускорение центра тяжести. Для звена 5. Положение механизма 3:
Положение механизма 7:
Положение механизма 10:
Для звена 4.
Для звена 3. Положение механизма 3:
Положение механизма 7:
Положение механизма 10:
Силы инерции направлены в сторону, противоположную ускорениям центров тяжести звеньев. Моменты сил инерции звеньев (Н·м) определяются по уравнению
где IS – момент инерции массы звена относительно оси, проходящей через его центр тяжести (кг·м2 ), e – угловое ускорение звена (1/с2 ). Момент инерции 3 звена, для 3, 7 и 10 соответственно
Моменты сил инерции направлены в сторону, противоположную угловым ускорениям звеньев. 3.4. Расчёт группы ВПП.Силовой расчет механизма начинают с группы Ассура, наиболее удаленной от группы начального звена, т.е. в данном случае с группы ВПП. В начале рассмотрим звено 4.
Из этого уравнения следует, что сила Сумма моментов для звена 4 относительно точки B позволяет вычислить момент в поступательной паре B, образованный звеньями 4 и 3,
Рассмотрим группу звеньев 4 - 5 :
Векторное уравнение сил для группы звеньев 4 - 5 дает возможность определить модули векторов сил F45 и F05 . Строим план сил с масштабным коэффициентом К F
=20 Н/м и находим
Для положений 3, 7, 10 соответственно:
Для определения реактивного момента в поступательной паре составим уравнение моментов для звенев 4 - 5 относительно точки Q и N
где NQ=500 мм – расстояние между опорами, остальные рычаги находим из плана положений, с учетом масштабного коэффициента. Для положения 3:
Для положения 7:
Для положения 10:
3.5. Расчёт группы ВВПДля определения силы F 12 составляем уравнение равновесия для звена BC. Для положения 3:
где h1 =795.02 мм, h2 =394.04 мм, h3 =67.73 мм, АС=459.26 мм– рычаги, взятые с плана положений.
Для положения 7:
где h1 =782 мм, h2 =402 мм, h3 =96 мм, АС=422 мм.
Для положения 10:
где h1 =804 мм, h2 =352 мм, h3 =36 мм, АС=278 мм.
Строим план сил для звена 3 по векторному уравнению
План сил замыкается искомыми векторами Направление F12 определяется из условия равновесия камня кулисы по векторному уравнению
3.6. Расчёт группы начального звена Из векторного уравнения сил для звена 1 графически определяем вектор F01 по величине и направлению :
Строим план сил с масштабным коэффициентом KF =200 H/мм. Соответственно для 3, 7, 10 положения: F10 =9993.5 H; F10 =3857.9 H; F10 =3028.3 H. Сумма моментов для звена 1 относительно точки О дает возможность найти значение движущего момента Mд1 :
Для положения 3:
Для положения 3:
Для положения 3:
4. ПРОЕКТИРОВАНИЕ ЭВОЛЬВЕНТНОГО ПРОФИЛЯ ЗУБЧАТЫХ КОЛЕС 4.1. Расчёт основных размеров колёс Исходные данные; число зубьев, зубчатых колес z1 =12, z2 =23; модуль m=3.5 Коэффициенты смещения: х1 =0.693, х2 =0.334, х∑ =1.027 по табл. 4(2). 1. Делительные диаметры:
Основные диаметры:
2. Угол зацепления:
где α=20˚- профильный угол рейки;
3. Делительное межосевое расстояние:
4. Межосевое расстояние:
5. Передаточное число:
6. Начальные диаметры:
7. Коэффициент воспринимаемого смещения:
8. Коэффициент уравнительного смещения:
9. Диаметры впадин:
10. Высота зуба:
11. Диаметры вершин зубьев:
12. Окружной делительный шаг:
13. Угловые шаги:
14. Окружные делительные толщины зубьев:
15. Начальные окружные толщины зубьев:
16. Угол профиля зуба на окружности вершин:
17. Окружные толщины зубьев по вершинам:
где 18. Радиусы кривизны эвольвенты на вершине зуба:
19. Длина линии зацепления:
20. Длина активной линии зацепления:
21. Угол перекрытия:
22. Коэффициент перекрытия:
23. Радиус кривизны эвольвенты в нижней точке активного профиля:
24. Радиус кривизны эвольвенты в граничной точке эвольвенты:
Построение картины зацепления. 1. Наносим центры колес. Строим начальные окружности Для построения профилей зубьев колес, находящихся в зацеплении, выбраем масштабный коэффициент Кs =0,008м/мм. Отрезок прямой, заключенный между точками N
1
и N
2
,
называют линией зацепления ( Построение эвольвентных профилей зубьев производим рассчитав предварительно толщину зубьев по ряду окружностей. Зададимся для этого последовательным рядом значений Таблица 3. Толщина зубьев шестерни
Таблица 4. Толщина зубьев колеса
Отложив по делительным окружностям окружные делительные толщины зубьев и разделив их пополам, найдем положения осей симметрии зубьев. Проведя окружности диаметром Профиль ножки зуба у ее основания формируется переходной кривой вершины зуборезной рейки, радиус которой равен Плавность работы зубчатой передачи характеризуется коэффициентом перекрытия В нашем примере
Это означает, что 18% времени контакта колес в зацеплении будут участвовать две пары зубьев и 82% времени — одна. Удельные скольжения Для шестерни Таблица 5.Значения удельного скольжения
Фактически зацепление происходит по активной линии зацепления, поэтому удельные скольжения целесообразно исследовать лишь в пределах Т.к. Оценка проектируемой передачи по геометрическим показателям производится в соответствии с ГОСТ 16532—70. При отсутствии подрезания зуба Принятые в расчетах коэффициенты смещений Для построения графика скоростей скольжения, находим относительную скорость скольжения
где РК - расстояние от полюса до любой точки К лежащей на линии зацепления
Выбираем масштабный коэффициент для графика скоростей скольжения
Для графика коэффициентов удельных скольжений выбираем Кi =0.05мм/мм. 4. СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА Исходные данные: х=0.039 м – максимальный подъем толкателя; lBN =0.12 м-длина толкателя; a1 /a2 =3 –соотношение между величинами ускорений толкателя. При проектировании кулачкового механизма необходимо обеспечить заданный закон движении толкателя (рис. 3—3) и осуществить подачу стола во время заднего перебега (о конце холостого и в начале рабочего ходов) в соответствии с циклограммой. Определим фазовые углы путем замера на плане положений и согласно циклограмме. Угол удаления jуд =56.72˚, угол дальнего стояния jд.с =151.7˚, угол сближения jсб =56.72˚,угол ближнего стояния jб.с =94.85˚. Рабочий угол jуд +jд.с +jсб =jраб =265.14˚ (51) Строим график Произвольно выбираем базу графика b=200 мм. Масштабный коэффициент по оси j
Задаем произвольно Методом обратного дифференцирования строим графики перемещений и аналога скоростей. Находим масштабные коэффициенты
Определяем минимальный радиус кулачка. Выбираем ординату и строим в масштабе
В выбранном масштабе разбиваем траекторию толкателя соответственно точкам на графике перемещений:
На линиях отложим значения аналогов скоростей:
Зная максимальный угол давления на толкателе θ=0,58 рад=33,23˚, строим зону возможных диаметров. Принимаем диаметр кулачка D=100 мм, экстриситет е=0,находим межосевое расстояние между осью кулачка и осью толкателя aw =156.2 мм. Определяем радиус ролика.
где ρ=58,75 мм - минимальный радиус кривизны кулачка, находится из построения. Принимаем из нормального ряда чисел Rр =20 мм. Строим профиль кулачка путем поворота толкателя вокруг оси кулачка, в масштабе КS =0,001 м/мм. Построение графика изменения угла давления. Из графика определения минимального радиуса кулачка определяем значения угла давления. Таблица 6. Значения угла давления
Строим график изменения угла давления в масштабе Кδ =0,01745 рад/мм. Определение жесткости пружины. Строим график, на котором по оси х откладываем значения хода толкателя с масштабным коэффициентом КН =0,001 м/мм. По оси у откладываем значения силы толкателя Fi с масштабным коэффициентом КF =0.02 Н/мм. Принимая массу толкателя m=2 кг и зная ускорение толкателя, находим силу:
С полученного графика находим Принимая предварительное натяжение пружины f0
=0.2 H и запас по усилию пружины
БИБЛИОГРАФИЯ 1. Методические указания по выполнению курсового проекта. Часть1 и 2. Свердловск 1978 г. 2. Кореняко Е.Ф. Курсовое проектирование механизмов и машин. М. Высшая школа. 1967г. 3. Попов С. А. Курсовое проектирование механизмов и машин. М. Высшая школа. 1986 г. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||






 (11)
(11)










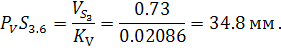








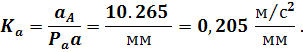





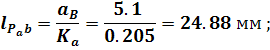

















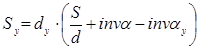 , где
, где