МГТУ «МАМИ»
Кафедра: «Теория механизмов и машин»
КУРСОВОЙ ПРОЕКТ
КИНЕМАТИЧЕСКИЙ И СИЛОВОЙ РАСЧЕТ МЕХАНИЗМА
Содержание
Исходные данные
1 Структурный анализ механизма
2 Кинематический анализ механизма
2.1 Построение планов механизма
2.2 Построение планов скоростей механизма
2.3 Построение планов ускорений механизма
3 Кинетостатический анализ механизма
3.1 Определение исходных данных для кинетостатического анализа
3.2 Определение реакций кинематических пар в структурной группе (звенья 2-3)
3.3 Силовой расчет ведущего звена
4 Кинематическое исследование зубчатого механизма
Список использованной литературы
Исходные данные
Схема 4

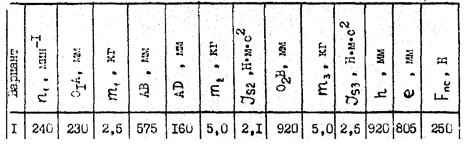
Выполнить: структурный, кинематический и кинетостатический анализ для положения кривошипа при φ = 2250
.
1 Структурный анализ механизма
Представим механизм в виде совокупности начального механизма и структурных групп.
Начальным механизмом называют механизм, состоящий из двух звеньев: 1, 0 (одно из них неподвижное — стойка), которые образуют одноподвижную пару (вращательную или поступательную). Структурная группа, или группа Ассура — кинематическая цепь, которая состоит из подвижных звеньев, соединенных между собой низшими одноподвижными кинематическими парами, и имеет число подвижностей группы (на плоскости), равное нулю.
Последовательность анализа:
· Выделяем звенья, образующие начальный механизм
· Определяем состав и вид групп Ассура, анализируя оставшиеся звенья, начиная со звеньев, наиболее удаленных от начального механизма.
Результаты структурного анализа представлены в табл. 1,2
Таблица 1
| Определение степени подвижности механизма -W |
Обозначения
КП
|
ЗвеньяКП |
Относ. движ. |
Подвижность
в КП
|
| O1
|
4-1 |
вращ |
1 |
| A |
1-2 |
вращ |
1 |
| B |
2-3 |
вращ |
1 |
| O2
|
3-4 |
вращ |
1 |
| Вид абсолютного движения звеньев механизма (наименование звеньев) |
Плоское (шатуны) |
2 |
| Вращательное (кривошипы, коромысла) |
1 |
3 |
| Поступательное (ползуны) |
| Траектории центровподвижныхшарниров |
Прямая |
| Окружность |
A |
B |
| Сложная кривая |
| Число звеньевмеханизма |
Общее (включая стойку) |
k=4 |
| совершающих движение |
n=3 |
| Число кинематических пар механизма |
вращательных |
p5в
=4 |
Всего 4
пятого класса p5
=4
|
| поступательных |
p5п
=0 |
| Число подвижностей механизма |
W=3∙n-2∙p5
=3∙3-2∙4=9-8=1 |
Вывод – число подвижностей механизма W=1. Это означает, что механизм имеет только одно начальное звено – кривошип 1. Также это означает, что механизм имеет только одну степень свободы в движении относительно стойки и достаточно задать только одну обобщенную координату движения (например, угол поворота кривошипа относительно исходного положения), чтобы определить положение всех звеньев механизма относительно стойки в данный момент времени.
Таблица 2
| Разбиение на структурные группы и определение их класса и порядка |
| Схема первичного механизма |
 |
| Число звеньев в группе |
2 |
| Число подвижных звеньев в группе |
n=1 |
| Число КП 5-ого класса в группе |
p5
=1 |
| Класс |
I |
Порядок |
1 |
| Подвижность механизма |
W=3∙n-2∙p5
=3∙1-2∙1=1 |
|
| Схема структурной группы |

|
| Число звеньев в группе |
2 |
| Число подвижных звеньев в группе |
n=2 |
| Число КП 5-ого класса в группе |
p5
=3 |
| Класс |
II |
Порядок |
2 |
| Подвижность группы |
W=3∙n-2∙p5
=3∙2-2∙3=0 |
|
Заданный механизм состоит из ведущего звена 1 со стойкой 4 и двухповодковой группы (звенья 2 - 3). Звено 1 вращается, совершая полный оборот, и называется кривошипом. Звено 3 совершает вращательное движение с неполным оборотом и называется коромыслом. Звено 2 совершает сложное движение и образует кинематические пары с кривошипом 1 и коромыслом 3. Такое звено называется шатуном. Все кинематические пары вращательные V класса.
Таким образом, заданный механизм является плоским с одной степенью свободы и называется кривошипно-коромысловым.
Схему такого механизма можно использовать для резки пруткового материала.
2 Кинематический анализ механизма
Основными задачами кинематического исследования механизмов являются:
· определение положений звеньев
· определение скоростей и ускорений точек;
· определение угловых скоростей и ускорений звеньев.
Ведущее звено - кривошип и считаем его угловую скорость 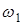 , рад/с постоянной. Исследования проводим графоаналитическими методами. Так, положения звеньев определяем методом засечек при построении плана механизма, скорости и ускорения различных точек механизма находим с помощью построения планов скоростей и ускорений. , рад/с постоянной. Исследования проводим графоаналитическими методами. Так, положения звеньев определяем методом засечек при построении плана механизма, скорости и ускорения различных точек механизма находим с помощью построения планов скоростей и ускорений.
2.1 Построение планов механизма
Кинематическую схему строим методом засечек.
Выбираем масштаб построения с таким расчетом, чтобы планы положений механизма заняли примерно 1/5…1/4 часть площади формата А1 или полную площадь формата А4.
Выбираем точку О1
. Проводим окружность радиуса 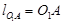 . Длину отрезка, изображающего звено О1
А выбираем произвольно из соображения размещения схемы механизма на листе выбранного формата. . Длину отрезка, изображающего звено О1
А выбираем произвольно из соображения размещения схемы механизма на листе выбранного формата.
O1
A = 230 мм – заданная длина кривошипа.
 = 46 мм - длина кривошипа на чертеже. = 46 мм - длина кривошипа на чертеже.
Вычисляем масштаб построения  ; ;
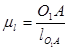 = 0,23 / 46 = 0,005 м/мм = 0,23 / 46 = 0,005 м/мм
В соответствии с выбранным масштабом определяем длины всех линейных величин.
Вычисляем длину отрезка АВ:  = 0,575 / 0,005 = 115 мм. = 0,575 / 0,005 = 115 мм.
Вычисляем длину отрезка О2
В:  = 0,92 / 0,005 = 184 мм. = 0,92 / 0,005 = 184 мм.
Вычисляем длину отрезка АD:  = 0,16 / 0,005 = 32 мм. = 0,16 / 0,005 = 32 мм.
Строим план механизма в заданном положении (φ = 2250.
) Заданное положение механизма, вычерчиваем основными линиями. (Остальные положения механизма вычерчиваем тонкими сплошными линиями). Вычерчиваем начальное звено О1
А в заданном положении. Из точки A делаем засечку радиусом  . Из точки О2
делаем засечку радиусом . Из точки О2
делаем засечку радиусом  . Находим место пересечения засечек – получаем положение точки B. Находим положение точки D. . Находим место пересечения засечек – получаем положение точки B. Находим положение точки D.
Разбиваем окружность на восемь равных частей. Строим 8 положений механизма, чтобы представить себе как он работает и какую траекторию описывает точка D. Последовательно помещаем шарнир А в равноотстоящие положения 2, 3…7, 8 в направлении вращения кривошипа, методом засечек определяем соответствующие положения точек B и в кривошипа.
Для получения траектории точки в необходимо последовательно соединить плавной кривой все восемь положений точки в с помощью лекал. Находим крайние положения механизма (M1
N1
ТВ1
и M2
N2
ТВ2
).
2.2 Построение планов скоростей механизма
Кривошип (1) вращается в направлении, указанном стрелкой с постоянной угловой скоростью  . .
Угловая скорость вращения кривошипа
 = = 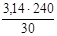 = 25,1 рад/с = 25,1 рад/с
На чертеже выбираем точку – полюс плана скоростей. Обозначим ее  . Скорость точки О1
равна нулю, т.е. отрезок на плане скоростей будет равен нулю – точка . Скорость точки О1
равна нулю, т.е. отрезок на плане скоростей будет равен нулю – точка  совпадет с точкой совпадет с точкой  . .
Вектор скорости точки А направлен перпендикулярно звену 1 в сторону направления вращения.
 = 25,1 ∙ 0,23 = 5,8 м/с = 25,1 ∙ 0,23 = 5,8 м/с
Вектор скорости точки S1
направлен перпендикулярно звену 1 в сторону направления вращения.
 = 25,1 ∙ 0,115 = 2,9 м/с = 25,1 ∙ 0,115 = 2,9 м/с
Из полюса (точки  ) построим вектор ) построим вектор 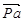 , соответствующий вектору скорости , соответствующий вектору скорости 
Вектор 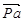 начинается в точке начинается в точке  , направлен перпендикулярно кривошипу. , направлен перпендикулярно кривошипу.
Конец вектора обозначим точкой 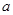 . .
После того, как длина вектора на чертеже определена, вычисляем масштаб построения планов скоростей:
 . .
Вектор на плане, соответствующий скорости центра тяжести первого звена 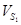 - - 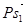 совпадет по направлению с вектором совпадет по направлению с вектором  , его длина будет зависеть от масштаба построения: , его длина будет зависеть от масштаба построения:
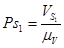 = =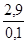 = 29 мм = 29 мм
Переходим к анализу линейных скоростей точек структурной группы (звенья 2, 3).
Звено 2 совершает плоскопараллельное движение, звено 3 вращательное.
Для нахождения скорости точки B составляем векторное уравнение:

Точка B движется по окружности с центром в О2
.
Векторное уравнение можно решить, если в нем не более двух неизвестных.
| Вектор, входящий в уравнение |
 |
 |
 |
| Направление вектора |
 - перпендикулярна О2
В - перпендикулярна О2
В |
 |
 |
| Модуль вектора (его численное значение) м/с |
? |
вычислено |
? |
Решаем векторное уравнение графически.
В правой части уравнения складываются два вектора 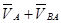 : :
1. Надо построить вектор соответствующий  - но он на плане уже есть, (отрезок - но он на плане уже есть, (отрезок ) – приходим в точку ) – приходим в точку 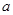 . Из точки . Из точки 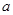 надо построить вектор, соответствующий надо построить вектор, соответствующий  , но для этого вектора задано только направление. Проводим из точки , но для этого вектора задано только направление. Проводим из точки 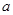 прямую прямую 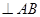 . .
2. Переходим к левой части уравнения – в ней указан только вектор  . Т.е. выходя из полюса надо построить вектор, соответствующий . Т.е. выходя из полюса надо построить вектор, соответствующий  . Но для него известно только направление – из точки . Но для него известно только направление – из точки  проводим прямую перпендикулярную О2
В. проводим прямую перпендикулярную О2
В.
Точка пересечения прямых – точка  . Расставляем стрелки, определяющие направление векторов. Направление в правой части уравнения задано вектором . Расставляем стрелки, определяющие направление векторов. Направление в правой части уравнения задано вектором 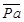 . Направление вектора в левой части уравнения – из полюса. Вектор . Направление вектора в левой части уравнения – из полюса. Вектор  на плане скоростей соответствует скорости на плане скоростей соответствует скорости  . .
Замеряем длины получившихся векторов ab, 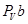 и, учитывая масштаб, вычисляем скорости: и, учитывая масштаб, вычисляем скорости:
 = 0,1 · 37,4 = 3,74 м/с; = 0,1 · 37,4 = 3,74 м/с;
 = 0,1 · 51,6 = 5,16 м/с. = 0,1 · 51,6 = 5,16 м/с.
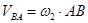 ; ;
Угловая скорость шатуна 
Для определения направления  мысленно переносим вектор мысленно переносим вектор 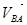 (вектор (вектор 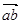 на плане скоростей) в точку В плана механизма и смотрим как будет вращаться звено 2 относительно точки А под действием этого вектора. на плане скоростей) в точку В плана механизма и смотрим как будет вращаться звено 2 относительно точки А под действием этого вектора.
Определяем скорость точки D.


 = =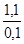 = 11 мм = 11 мм
Вектор, соответствующий  направлен направлен  . .
Проведя построения на плане скоростей, находим вектор, соответствующий 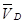 . .
 = 0,1 · 48,7 = 4,87 м/с. = 0,1 · 48,7 = 4,87 м/с.
Аналогично находим скорость точки S2
.

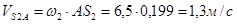
АS2
= 39,8 ∙ 0,005 = 0,199 м
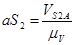 = = = 13 мм = 13 мм
Вектор, соответствующий  направлен направлен  . .
Проведя построения на плане скоростей, находим вектор, соответствующий  . .
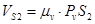 = 0,1 · 49,6 = 4,96 м/с. = 0,1 · 49,6 = 4,96 м/с.
Коромысло 3 вращается относительно точки О2
. Угловая скорость коромысла
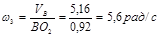
Для определения направления  мысленно переносим вектор мысленно переносим вектор  ( вектор ( вектор  на плане скоростей) в точку В плана механизма и смотрим, как будет вращаться звено 3 под действием этого вектора. на плане скоростей) в точку В плана механизма и смотрим, как будет вращаться звено 3 под действием этого вектора.
Вектор скорости точки S3
направлен перпендикулярно звену 3 в сторону направления вращения.
 = 5,6 ∙ 0,46 = 2,6 м/с = 5,6 ∙ 0,46 = 2,6 м/с
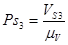 = =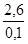 = 26 мм = 26 мм
2.3 Построение планов ускорений механизма
Кривошип вращается в направлении, указанном стрелкой с постоянной угловой скоростью 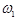 . .
В общем случае ускорение точки вращающегося тела складывается из векторов ускорения нормального и ускорения тангенциального.
Вектор нормального ускорения точки направлен из точки к центру вращения и зависит от угловой скорости звена и расстояния точки от центра вращения. Вектор тангенциального ускорения точки направлен по касательной к траектории её движения (т.е.перпендикулярен ускорению нормальному) и зависит от углового ускорения вращения и расстояния точки от центра вращения.
Угловая скорость кривошипа постоянна, угловое ускорение равно нулю  , тангенциальная составляющая ускорения точки А равна нулю , тангенциальная составляющая ускорения точки А равна нулю  . .
Ускорение точки А равно нормальному ускорению и направлено вдоль звена 1 к центру вращения
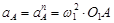 = 25,12
∙ 0,23 = 145 м/с2 = 25,12
∙ 0,23 = 145 м/с2
Ускорение точки  равно нормальному ускорению этой точки и направлено вдоль звена 1 к центру вращения равно нормальному ускорению этой точки и направлено вдоль звена 1 к центру вращения
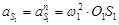 = 25,12
∙ 0,115 = 72,5 м/с2 = 25,12
∙ 0,115 = 72,5 м/с2
На чертеже выбираем точку – полюс. Обозначим ее  . Ускорение точки О1
равно нулю, т.е. отрезок на плане скоростей будет равен нулю – точка О1
совпадет с точкой . Ускорение точки О1
равно нулю, т.е. отрезок на плане скоростей будет равен нулю – точка О1
совпадет с точкой  . .
Откладываем из полюса параллельно звену О1
А вектор  , соответствующий ускорению , соответствующий ускорению  . .
Вычисляем масштаб построения 

Построим на плане вектор  . Его длина на чертеже: . Его длина на чертеже:
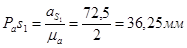 . Направление совпадает с . Направление совпадает с  . .
Шатун (звено 2) совершает плоско-параллельное движение (ускорение точек такого звена складывается из ускорения полюса и ускорений, возникающих при повороте звена относительно полюса)
Если рассматривать точку В как принадлежащую звену 2, то можно записать: 
Коромысло (звено 3) совершает вращательное движение относительно точки О2
.
Если рассматривать точку В как принадлежащую звену 3,то: 
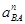 - вектор нормальной составляющей ускорения в движении точки В относительно А, направленный по ВА от точки В к точке А: - вектор нормальной составляющей ускорения в движении точки В относительно А, направленный по ВА от точки В к точке А:
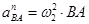 = 6,52
∙ 0,575 = 24,3 м/с2 = 6,52
∙ 0,575 = 24,3 м/с2
 - вектор тангенциальной составляющей ускорения в движении точки В относительно точки А, направление которого перпендикулярно к нормальной составляющей ускорения, т.е. перпендикулярно к АВ. - вектор тангенциальной составляющей ускорения в движении точки В относительно точки А, направление которого перпендикулярно к нормальной составляющей ускорения, т.е. перпендикулярно к АВ.
 - вектор нормальной составляющей ускорения в движении точки В относительно неподвижной точки 02
, направленный вдоль В02
от точки В к точке О2 - вектор нормальной составляющей ускорения в движении точки В относительно неподвижной точки 02
, направленный вдоль В02
от точки В к точке О2
 = 5,62
∙ 0,92 = 28,9 м/с2 = 5,62
∙ 0,92 = 28,9 м/с2
 - вектор тангенциальной составляющей ускорения в движении точки В относительно точки O2
, направление которого перпендикулярно к нормальной составляющей - вектор тангенциальной составляющей ускорения в движении точки В относительно точки O2
, направление которого перпендикулярно к нормальной составляющей  , т.е. перпендикулярно к O2
B). , т.е. перпендикулярно к O2
B).

Решаем векторное уравнение:
1) Из полюса 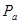 переходим в точку переходим в точку 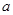 , из точки , из точки 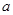 проводим прямую параллельно АВ и откладываем проводим прямую параллельно АВ и откладываем  , что соответствует вектору нормального ускорения в повороте точки В относительно А, и получаем точку , что соответствует вектору нормального ускорения в повороте точки В относительно А, и получаем точку  . .

Теперь надо построить вектор соответствующий  , но у него задано только направление. Из точки , но у него задано только направление. Из точки  проводим линию проводим линию  . .
2) Из полюса откладываем 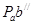 параллельно О2
В в направлении от В к О2
, что соответствует вектору нормального ускорения точки В относительно О2
, и получаем точку параллельно О2
В в направлении от В к О2
, что соответствует вектору нормального ускорения точки В относительно О2
, и получаем точку 
 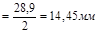
Из точки  надо построить вектор, соответствующий надо построить вектор, соответствующий  , но у него известно только направление. Из точки , но у него известно только направление. Из точки  проводим линию проводим линию  . .
3) Линии, проведенные из точек  и и  , пересекаются в точке , пересекаются в точке 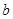 . Проводим вектор . Проводим вектор 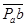 - вектор соответствует ускорению точки В. - вектор соответствует ускорению точки В.
Указываем на плане направления всех векторов.
Замеряем на плане длины полученных отрезков и вычисляем ускорения:
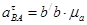 = 69,4 ∙ 2 = 138,8 м/с2
. = 69,4 ∙ 2 = 138,8 м/с2
.
 = 70,5 ∙ 2 = 141 м/с2
. = 70,5 ∙ 2 = 141 м/с2
.
 = 45,5 ∙ 2 = 91 м/с2
. = 45,5 ∙ 2 = 91 м/с2
.
 = 47,7 ∙ 2 = 95,4 м/с2
. = 47,7 ∙ 2 = 95,4 м/с2
.
Вычисляем угловые ускорения:
Угловое ускорение шатуна (2-е звено): 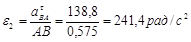
Угловое ускорение коромысла (3-е звено): 
Направления угловых ускорений определяются в соответствии с направлениями  и и  . .
Для определения направления  мысленно переносим вектор мысленно переносим вектор  (вектор (вектор 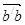 на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 2 относительно точки А под действием этого вектора. В нашем случае угловое ускорение на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 2 относительно точки А под действием этого вектора. В нашем случае угловое ускорение  направлено по ходу часовой стрелки. направлено по ходу часовой стрелки.
Для определения направления  мысленно переносим вектор мысленно переносим вектор  (вектор (вектор 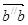 на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 3 относительно точки О2
под действием этого вектора. на плане ускорений) в точку В плана механизма и смотрим в какую сторону будет вращаться звено 3 относительно точки О2
под действием этого вектора.
Составляем векторное уравнение для определения ускорения 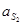

 = 6,52
∙ 0,199 = 8,4 м/с2
. = 6,52
∙ 0,199 = 8,4 м/с2
.
 
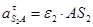 = 241,4 ∙ 0,199 = 48 м/с2 = 241,4 ∙ 0,199 = 48 м/с2
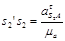 
Вектор, входящий
в уравнение
|
 |
 |
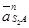 |
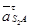 |
| Направление вектора |
? |
на плане |
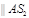 ; ;
от S2
к A
|
 в сторону определяемуюнаправлением в сторону определяемуюнаправлением   |
Модуль вектора (его
численное значение) м/с2
|
? |
вычислено |
вычислено |
вычислено |
Решаем векторное уравнение графически:
1) Из полюса  переходим в точку переходим в точку 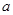
2) Отложив на плане от точки a вектор 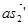 , получим точку , получим точку  . Направление вектора . Направление вектора 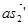 - параллельно АS2
. Через полученную точку - параллельно АS2
. Через полученную точку  проводим линию проводим линию  . .
3) Из точки  вдоль проведенной линии откладываем вектор вдоль проведенной линии откладываем вектор 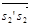
4) из полюса  - стоим вектор - стоим вектор 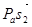
Измеряем длину отрезка 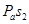 . Вычисляем . Вычисляем 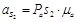 = 61,6 ∙ 2 = 123,2 м/с2 = 61,6 ∙ 2 = 123,2 м/с2
Аналогично находим ускорение точки D.

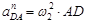 = 6,52
∙ 0,16 = 6,8 м/с2
. = 6,52
∙ 0,16 = 6,8 м/с2
.
 
 = 241,4 ∙ 0,16 = 38,6 м/с2 = 241,4 ∙ 0,16 = 38,6 м/с2
 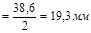
Вычисляем  = 86,2 ∙ 2 = 172,4 м/с2 = 86,2 ∙ 2 = 172,4 м/с2
Находим ускорение точки S3
.

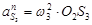 = 5,62
∙ 0,46 = 14,4 м/с2
. = 5,62
∙ 0,46 = 14,4 м/с2
.
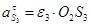 = 98,9 ∙ 0,46 = 45,5 м/с2 = 98,9 ∙ 0,46 = 45,5 м/с2
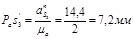
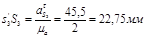
 = 23,9 ∙ 2 = 47,8 м/с2 = 23,9 ∙ 2 = 47,8 м/с2
3 Кинетостатический анализ механизма
3.1 Определение исходных данных для кинетостатического анализа
На механизм действуют активные нагрузки: силы веса, главные векторы сил инерции, главные моменты сил инерции, сила полезного сопротивления, уравновешивающая сила.
Силы тяжести
:
G1
= m1
g = 2,5 ∙ 9,8 = 24,5 Н.
G2
= m2
g = 5,0 ∙ 9,8 = 49 Н.
G3
= m3
g = 5,0 ∙ 9,8 = 49 Н.
m1
, m2
, m3
– массы стержней.
Сила тяжести прикладывается в центре тяжести каждого стержня, направлена вертикально вниз.
Главные векторы сил инерции
:
Fин1
= m1
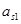 = 2,5 ∙ 72,5 = 181,3 Н. = 2,5 ∙ 72,5 = 181,3 Н.
Fин2
= m2
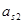 = 5,0 ∙ 123,2 = 616 Н. = 5,0 ∙ 123,2 = 616 Н.
Fин 3
= m3
 = 5,0 ∙ 47,8 = 239 Н. = 5,0 ∙ 47,8 = 239 Н.
Главный вектор сил инерции прикладывается в центре тяжести каждого стержня, направлен в сторону противоположную направлению ускорения центра тяжести.
Главные моменты сил инерции:
Mин1
= Is
1
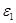 = 0 т.к. = 0 т.к. 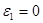
Mин
2
= Is2
 = 2,1 ∙ 241,4 = 506,9 Н∙м = 2,1 ∙ 241,4 = 506,9 Н∙м
Mин
3
= Is3
 = 2,5 ∙ 98,9 = 247,3 Н∙м = 2,5 ∙ 98,9 = 247,3 Н∙м
Is
1
– момент инерции звена 1 относительно оси, проходящей через центр масс звена 1 перпендикулярно к плоскости движения.
Is
2
- момент инерции звена 2 относительно оси, проходящей через центр масс звена 2 перпендикулярно к плоскости движения.
Is
3
- момент инерции звена 3 относительно оси, проходящей через центр масс звена 3 перпендикулярно к плоскости движения.
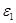 , ,  , ,  - угловые ускорения звеньев. - угловые ускорения звеньев.
Главный момент сил инерции направлен в сторону противоположную направлению углового ускорения
Сила полезного сопротивления – Fпс
– сила приложена в точке в и направлена в сторону противоположную направлению скорости точки D.
Уравновешивающая сила – Fур
– требуется определить. Сила приложена в точке А перпендикулярно кривошипу. Направление силы выбираем произвольно. Если направление будет выбрано не правильно, то числовое значение силы в результате расчета получится со знаком минус. Это будет означать, что направление силы противоположно указанному на расчетной схеме.
В результате кинетостатичекого (силового) анализа требуется определить силу Fур
и силы, действующие в шарнирах.
3.2 Определение реакций кинематических пар в структурной группе (звенья 2-3)
Вычерчиваем в масштабе структурную группу в заданном положении. Для определения реакций отсоединяем от нее стойку в точке O2
и ведущее звено 1 в шарнире А. Прикладываем все действующие силы, соблюдая их направление. Сами силы вычерчиваем без соблюдения масштаба. структурную группу в заданном положении. Для определения реакций отсоединяем от нее стойку в точке O2
и ведущее звено 1 в шарнире А. Прикладываем все действующие силы, соблюдая их направление. Сами силы вычерчиваем без соблюдения масштаба.
Отброшенные связи заменяем силами реакций. В точке А – реакция заменяет действие звена 1 на звено 2. В точке О2
– реакция заменяет действие звена 4 (стойки) на звено 3.
Т.к. направление реакций пока неизвестно, представим их в виде двух взаимно перпендикулярных составляющих.
В точке А приложим две составляющие 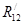 и и 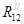 . . 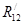 направим вдоль АВ. направим вдоль АВ. 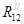 направим перпендикулярно АВ. направим перпендикулярно АВ.
В точке О2
приложим две составляющие 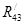 и и 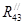 . . 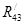 направим вдоль оси стержня 3. направим вдоль оси стержня 3. 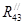 направим перпендикулярно оси стержня 3. направим перпендикулярно оси стержня 3.
Направление реакций выбираем произвольно. Если в результате вычислений получится знак минус, то следует сменить направление на противоположное. После этого силу следует считать положительной.
Составляем уравнения равновесия:
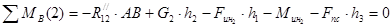
Измеряем на плане структурной группы длину h1
, h2
и h3
. Решаем уравнение. Находим значение 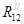
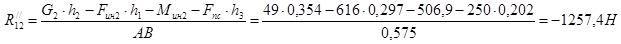

Измеряем на плане структурной группы длину h4
и h5
. Решаем уравнение. Находим значение 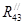

Векторная сумма всех сил, действующих на систему тел находящихся в равновесии равна нулю.
Составляем векторное уравнение равновесия структурной группы 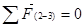
Для облегчения решения векторного уравнения запишем входящие в него силы в определенной последовательности:
1) силы группируются по звеньям;
2) две составляющие одной и той же силы записываются рядом;
3) неизвестные силы записываются по краям уравнения.

Ноль в правой части уравнения означает, что при векторном сложении сил должен получиться замкнутый силовой многоугольник.
Векторное уравнение решаем графически.
Выбираем масштаб построения. Для выбора масштаба плана сил  используем самую большую по величине известную силу с таким расчетом, чтобы план сил поместился на запланированной для него площади листа. используем самую большую по величине известную силу с таким расчетом, чтобы план сил поместился на запланированной для него площади листа.
Масштаб будет равен

Теперь, чтобы определить длину любого вектора силы на чертеже, необходимо числовое значение силы разделить на масштаб  . .
План сил строится в той же последовательности, в какой записано векторное уравнение:
1) Для вектора 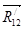 известно только направление. Проводим на листе прямую, параллельную известно только направление. Проводим на листе прямую, параллельную 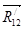 . Берем на прямой произвольную точку 1. . Берем на прямой произвольную точку 1.
2) Из точки 1 в масштабе строим вектор 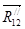 - приходим в точку 2. - приходим в точку 2.
3) Из точки 2 в масштабе строим вектор  - приходим в точку 3. - приходим в точку 3.
4) Из точки 3 в масштабе строим вектор  - приходим в точку 4. - приходим в точку 4.
5) Из точки 4 в масштабе строим вектор 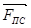 - приходим в точку 5. - приходим в точку 5.
6) Из точки 5 в масштабе строим вектор 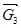 - приходим в точку 6. - приходим в точку 6.
7) Из точки 6 в масштабе строим вектор  - приходим в точку 7. - приходим в точку 7.
8) Из точки 7 в масштабе строим вектор 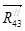 - приходим в точку 8. - приходим в точку 8.
9) Из точки 8 проводим прямую параллельную вектору 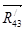 до пересечения с прямой, которую провели самой первой. Точку пересечения прямых – полюс плана – обозначим до пересечения с прямой, которую провели самой первой. Точку пересечения прямых – полюс плана – обозначим  . .
10) Указываем на плане направления векторов 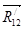 и и 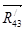 в соответствии с направлением обхода силового многоугольника – надо из полюса выйти и в полюс вернуться. в соответствии с направлением обхода силового многоугольника – надо из полюса выйти и в полюс вернуться.
11) Используя векторные равенства  и и 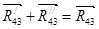 строим на плане векторы реакций в шарнире A (вектор строим на плане векторы реакций в шарнире A (вектор 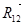 ) и в шарнире O2
(вектор ) и в шарнире O2
(вектор  ) )
12) Для определения реакции в шарнире В нужно рассмотреть равновесия одного из звеньев. Запишем векторное уравнение равновесия звена 2:

Т.е. реакцию в шарнире В (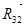 ) можно построить на плане сил, соединив конец вектора ) можно построить на плане сил, соединив конец вектора 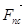 с началом вектора с началом вектора 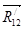 . .
13) Определить численные значения реакций в шарнирах А, В, О2
. Для этого надо измерить длину соответствующего вектора на плане сил и умножить её на масштаб  . .
R12
= 136 ∙ 10 = 1360 H.
R43
= 82,3 ∙ 10 = 823 H.
R32
= 78,8 ∙ 10 = 788 H.
3.3 Силовой расчет ведущего звена
В задачу силового расчета ведущего звена входит определение уравновешивающей силы и реакции в шарнире О1
для заданного положения.
Вычерчиваем ведущее звено в ранее выбранном масштабе  в заданном положении и прикладываем к нему силу тяжести звена - G1
, силу инерции - Fин1
, уравновешивающую силу - Fур
, силу реакции R21
, с которой звено 2 действует на звено 1. Сила реакции R21
равна по величине и противоположна по направлению силе R12
. Уравновешивающая сила Fур
, величину которой надо определить, приложена к шарниру А и направлена перпендикулярно к оси кривошипа. Предположим, что Fур
направлена в сторону вращения кривошипа. В шарнире О1
действует реакция со стороны стойки R41
, величина и направление которой неизвестны. в заданном положении и прикладываем к нему силу тяжести звена - G1
, силу инерции - Fин1
, уравновешивающую силу - Fур
, силу реакции R21
, с которой звено 2 действует на звено 1. Сила реакции R21
равна по величине и противоположна по направлению силе R12
. Уравновешивающая сила Fур
, величину которой надо определить, приложена к шарниру А и направлена перпендикулярно к оси кривошипа. Предположим, что Fур
направлена в сторону вращения кривошипа. В шарнире О1
действует реакция со стороны стойки R41
, величина и направление которой неизвестны.
Величину уравновешивающей силы определим из уравнения равновесия звена 1
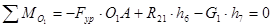

Длины h6
и h7
берем на чертеже. Уравнение решаем и определяем числовое значение Fур
.
Неизвестную по величине и направлению реакцию R41
определить из векторного уравнения равновесия звена 1:
 
Уравнение решаем графически, строя замкнутый силовой многоугольник. Для определения численного значения R41
измеряем на чертеже длину соответствующего вектора и умножаем на масштаб  . .
R41
= 151,6 ∙ 10 = 1516 H.
4 Кинематическое исследование зубчатого механизма
Исходные данные.
Схема 4.

| Z1
|
Z2
|
Z2’
|
Z3
|
Z3’
|
Z4
|
Z5
|
| 1 |
72 |
48 |
45 |
75 |
17 |
40 |
97 |
Требуется для заданной схемы зубчатого механизма определить общее передаточное отношение, угловую скорость (частоту вращения) выходного вала и направление его вращения. Угловую скорость на входе (скорость вращения зубчатого колеса 1) принять равной 1100 об/мин.
Вычертим кинематическую схему зубчатого механизма.
Обозначим звенья механизма цифрами, а кинематические пары заглавными латинскими буквами.
А, В, E, L, N - кинематические пары пятого класса, низшие.
С, D, К, М - кинематические пары четвертого класса, высшие.
Общее число звеньев механизма (включая стойку) k=6.
Число звеньев механизма совершающих движение n=5.
Число кинематических пар четвертого класса p4в
=4.
Число кинематических пар пятого класса p5в
=5.
Степень подвижности механизма  =3∙5-2∙5-4=1. =3∙5-2∙5-4=1.
Заданный зубчатый механизм мысленно разбиваем на зоны.
I часть механизма (1-3) – двухступенчатая зубчатая передача.
II часть (3/
- H) – планетарный редуктор (3, 5-центральные колеса; 5- опорное колесо; 4 – сателлит; Н – водило).
Входное звено всего механизма – зубчатое колесо 1.  . .
Выходное звено – водило H.
Требуется определить:
· передаточное отношение механизма 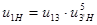 , ,
· скорость и направление вращения на выходе  . .
Определяем передаточное отношение I части механизма.
Передаточное отношение одной пары колес показывает, во сколько раз скорость ведущего колеса отличается от скорости ведомого колеса. Передаточное отношение зависит от числа зубьев колес ( , ,  ) и типа зацепления (внешнее, внутреннее). ) и типа зацепления (внешнее, внутреннее).
Передаточное отношение двухступенчатой зубчатой передачи:
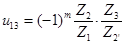
Z1
=72, Z2
=48, Z2’
=45, Z3
=75.
Число внешних зацеплений m=2
 1,111 1,111
Определяем передаточное отношение II части механизма.
Требуется определить передаточное отношение от подвижного колеса (3’) к водилу (H) - 
Верхний индекс (5) указывает какое звено неподвижно. В данном случае неподвижным является центральное опорное колесо 5.
Основным параметром, определяющим свойства планетарного механизма, является внутреннее передаточное отношение. Оно определяется как отношение частоты вращения малого центрального к частоте вращения большого центрального колеса при остановленном водиле.
Мысленно остановим водило, освободим опорное центральное колесо – получим обычную многоступенчатую передачу.
Определим передаточное отношение от малого подвижного колеса 3’ к колесу, которое в планетарном механизме было неподвижным - 5. (Верхний индекс в обозначении передаточного числа показывает, какое звено неподвижно – неподвижно сейчас водило).
Количество внешних зацеплений m=1
 =-5,7 =-5,7
2. Чтобы получить передаточное отношение от подвижного колеса к водилу в заданном механизме, необходимо полученный результат вычесть из 1:
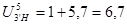
Определяем общее передаточное отношение механизма.
 =1,111∙6,7=7,44 =1,111∙6,7=7,44
Определяем скорость и направление вращения на выходе 
Знак плюс указывает на то, что колесо 1 и водило H, вращаются в одну сторону.
 ; ; 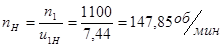
Список использованной литературы
1. Артоболевский И.И. Теория механизмов и машин. М., 1975г.
2. Петрова Т.М., Дмитриева Л.Н. Методические указания по теории механизмов и машин «Кинематический и силовой расчет механизма», М., МАМИ, 1990г.
|