Министерство Образования Российской Федерации

ИрГТУ

Кафедра АПП

Курсовая работа

по математике

Выполнил: студент группы АТП-05-1

Поверил: профессор

Баев А. В.

Иркутск

2007 г

Задание.

1. Для заданной электрической цепи составить дифференциальные уравнения при входном воздействии типа скачка.

2. Применить к полученному уравнению преобразование Лапласа при нулевых начальных условиях.

3. Решить уравнение операторным методом.

4. Построить переходный процесс.

5. Записать выражение и построить частотные характеристики цепи: АЧХ, ФЧХ, ДЧХ, МЧХ и АФЧХ (амплитудно-фазовую характеристику).

6. Описать динамику вашей цепи в терминах пространства состояния.

Схема электрической цепи

Дано:

R = 5

L = 10

C = 12

;

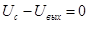
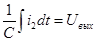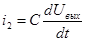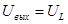
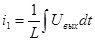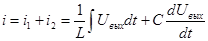
При подстановке данных получаем окончательное дифференциальное уравнение:

Применим преобразование Лапласа и запишем передаточную функцию для данной цепи

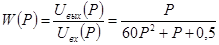
Решаем характеристическое уравнение:

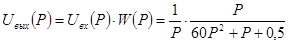
График переходного процесса

Заменим P = jω , получая комплексную переменную:

Решаем алгебраически:

АФЧХ :

ДЧХ :

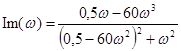
ФЧХ :

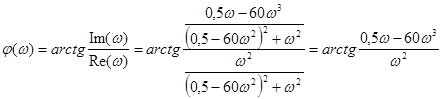
С помощью MathCAD строим все виды характеристик цепи:

Графики частотных характеристик цепи:

ДЧХ и МЧХ:

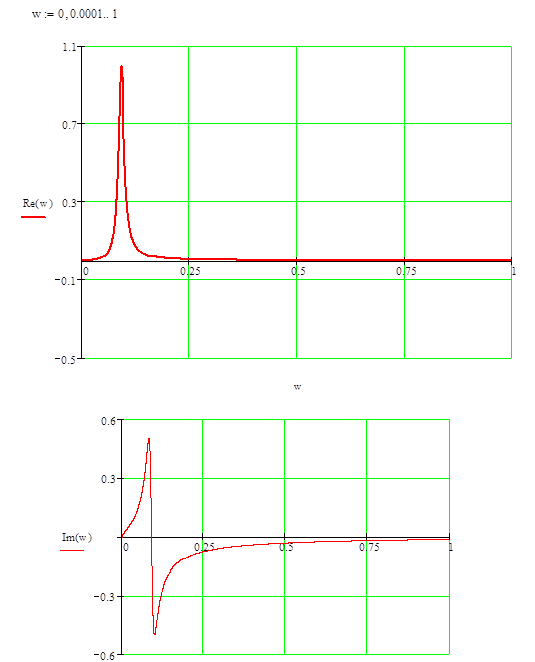
АЧХ:

ФЧХ:

АФЧХ:

Опишем динамику нашей цепи в терминах пространства состояния.

Компактная форма:

Составляем матрицу A:

Составляем матрицу единичную матрицу Ep:

Выражение для передаточной функции:

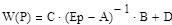
Составляем матрицу из алгебраического дополнения:

Составляем транспонированную матрицу:

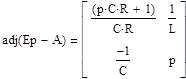
Находим определитель ∆

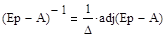
Выражение для передаточной функции:

При подстановке данных, получаем:

Дискретная форма.

Передаточная функция равна:

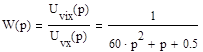
Находим корни корни характеристического уравнения:

Из таблицы оригиналов и значений:

Произведем подстановку данных:

Разделим числитель и знаменатель на z в max степени:

Следовательно:

где m- максимальная степень z, L- максимальная степень z в знаменателе:

Находим, целю часть:

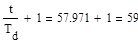
Следовательно:

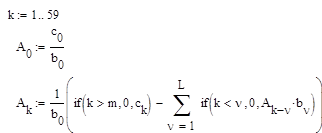
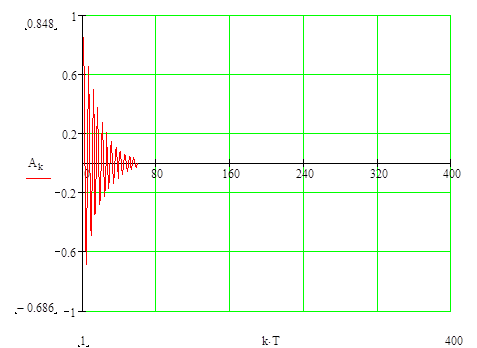
График дискретной функции :