Вступ
Введення поняття степеня з ірраціональним показником
Означення поняттястепеня з ірраціональним показником
Узагальнення поняття степеня
Список літератури
Вступ
З поняттям степені з ірраціональним показником учні ознайомуються або у 10 або у 11(12) классі залежно від профілю навчання та навчального закладу. Якщо розглянути підручник Бурда М.І. Дубінчук О.С. Мальований Ю.І. Математика 10-11 для шкіл, ліцеїв та гімназій гуманітарного профілю, то це поняття вводиться в 11 класі, причому, воно узагальнюється до поняття степеня з дійсним показником, у підручнику Бевз В.Г. Алгебра 10-11 для загальноосвітніх шкіл, з цим матеріал учні знайомляться ще в 10 класі.
Введення поняття
Після того, як для будь-якого дійсного числа ми визначили операцію пінесення до натурального степеня, для будь-якого 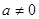 ми визначили операцію піднесення до нульового степеня та цілий від'ємний степінь, для будь-якого ми визначили операцію піднесення до нульового степеня та цілий від'ємний степінь, для будь-якого  – у додатний дробовий степінь, для будь-якого – у додатний дробовий степінь, для будь-якого  – у від'ємний дробовий степінь, з'являється питання: чи можна якимось чином визначити операцію піднесення до ірраціонального степеня, тобто визначити зміст виразу – у від'ємний дробовий степінь, з'являється питання: чи можна якимось чином визначити операцію піднесення до ірраціонального степеня, тобто визначити зміст виразу 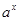 , для будь-якого дійсного х. , для будь-якого дійсного х.
Виявляється, що для додатних чисел а
можна надати сенсу запису 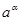 , , . .
Для цього треба розглянути 3 випадки:а=1, а
>1, 0<
a
<1
1) а=1
,то за визначенням . .
2) Якщо а
>1
, то оберемо будь-яке раціональне число  , та будь- яке раціональне число , та будь- яке раціональне число 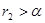 , тоді очевидно, що , тоді очевидно, що  , а тому , а тому  . Але . Але  , та оскільки а
>1
,
тоді , та оскільки а
>1
,
тоді і нарешті і нарешті
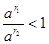 , тобто , тобто  . .
Під 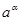 розуміють таке число, яке лежить між розуміють таке число, яке лежить між  та та 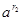 , при будь-якому виборі , при будь-якому виборі  та та 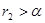 . Можна довести, що число . Можна довести, що число 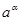 єдине для будь-якого а
>1
та ірраціонального єдине для будь-якого а
>1
та ірраціонального 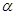 . .
3) Якщо 0<
a
<1
, тооберемо будь-яке раціональне число  , та будь- яке раціональне число , та будь- яке раціональне число 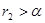 , тоді очевидно, що , тоді очевидно, що  , а тому , а тому  . .
Під 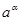 розуміють таке число, яке лежить між розуміють таке число, яке лежить між  та та 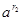 , при будь-якому виборі , при будь-якому виборі  та та 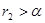 . Можна довести, що число . Можна довести, що число 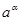 єдине для будь-якого 0<
a
<1
та ірраціонального єдине для будь-якого 0<
a
<1
та ірраціонального 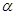 . .
Розглянемо приклади:
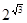 Для визначення степеня обирають 2 послідовності: Для визначення степеня обирають 2 послідовності:
 1; 1,7; 1,73; … 1; 1,7; 1,73; …
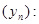 2; 1,8; 1,74;… 2; 1,8; 1,74;…
Причому, ці послідовності такі, що 
Отримаємо наближення 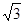 з надлишком та недостачею. Звідси отримаємо з надлишком та недостачею. Звідси отримаємо 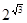 з надлишком та недостачею. з надлишком та недостачею.
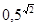 Для визначення степеня обирають 2 послідовності: Для визначення степеня обирають 2 послідовності:
 1,4; 1,41; 1,414; … 1,4; 1,41; 1,414; …
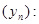 1,5; 1,42; 1,415;… 1,5; 1,42; 1,415;…
Причому, ці послідовності такі, що 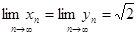
Отримаємо наближення 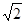 з надлишком та недостачею. Звідси отримаємо з надлишком та недостачею. Звідси отримаємо 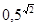 з надлишком та недостачею. з надлишком та недостачею.
Якщо 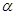 - від'ємне ірраціональне число ( - від'ємне ірраціональне число (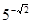 , ,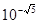 ), тоді вираз має той же самий сенс, який маєть степені із від'ємним раціональним показником: ), тоді вираз має той же самий сенс, який маєть степені із від'ємним раціональним показником:
 та та  . .
Означення
поняття
А тепер дамо означення степеня з ірраціональним показником:
Означення
Степенем з ірраціональним показником 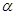 та основою а,
де а
>
0,
називається дійсне число та основою а,
де а
>
0,
називається дійсне число 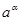 , яке є границею послідовності , яке є границею послідовності  , де , де 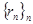 - послідовність раціональних чисел така, що границя - послідовність раціональних чисел така, що границя 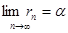 . .
Узагальнення поняття степеня
Узагальнимо поняття степеня:
Означення
Степенем 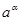 з дійсним показником з дійсним показником 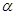 та основою а,
де а
>
0,
називається границя послідовності та основою а,
де а
>
0,
називається границя послідовності  , де , де 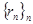 - послідовність раціональних чисел така, що границя - послідовність раціональних чисел така, що границя 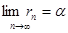 . .
При цьому для степеня з будь-яким дійсним показником справджуються ті ж самі властивості, як і для степеня з раціональним показником, а саме:
1) 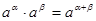 , ,   . .
2)  , ,   . .
3) 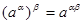 , ,   . .
4)  , ,   . .
5)  , ,   . .
6) 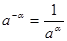 , , , , . .
Список літератури
1. Шкіль М.І., Слєпкань З.І., Дубинчук О.С. Алгебра і початки аналізу: Підруч. для 11 кл. загальноосвіт. навч. закл. – К.: Зодіак-ЕКО, 2006. – 384 с.
2. Бевз Г.П. Алгебра і початки аналізу: Підруч. для 10–11 кл. загальноосвіт. навч. закл. – К.: Освіта, 2005. – 255 с.
3. Бурда М.І., Дубінчук О.С., Мальований Ю.І. Математика 10-11: Навч. посіб. для шкіл, ліцеїв та гімназій гуманітарного профілю. – К.: Освіта,2004. – 223с.
4. Алгебра и начала анализа. 10-11 класс. А.Н. Колмогоров - 2001. – 320с.
|