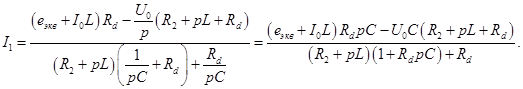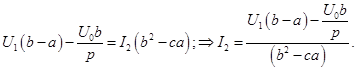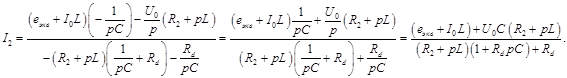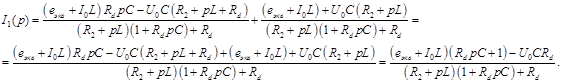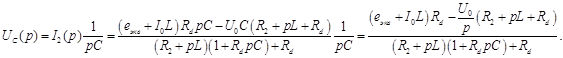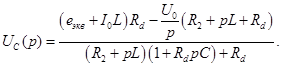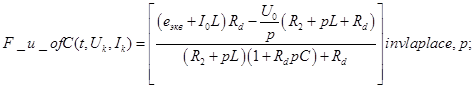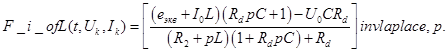Курсовая работа: Трехфазные выпрямители
|
Название: Трехфазные выпрямители Раздел: Промышленность, производство Тип: курсовая работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
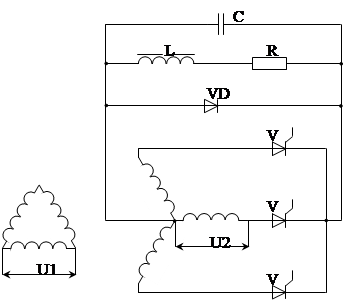
1. Трехфазные выпрямители Схемы выпрямителей трехфазного питания применяются в основном для питания потребителей средней и большой мощности. Первичная обмотка трансформаторов таких выпрямителей состоит из трех фаз и соединяется либо в звезду, либо в треугольник. Вторичные обмотки трансформатора (их может быть несколько) также трехфазные. С помощью специальных схем соединения вторичных обмоток и всего выпрямителя можно получить выпрямление напряжение с числом пульсаций за период Выпрямители трехфазного питания равномерно нагружают сеть трехфазного тока и отличаются высоким коэффициентом использования трансформатора. Схемы выпрямителей трехфазного питания используются для питания статических нагрузок активного и активно-индуктивного характера, статических нагрузок с противо-э.д.с., а также динамических нагрузок в виде электродвигателей постоянного тока. Последний вид нагрузки следует рассматривать как противо-э.д.с. с индуктивностью. 2. Схема с нулевым выводом (схема Миткевича) Составным элементом сложных схем выпрямителей трехфазного питания является простая трехфазная схема с нулевым выводом, предложенная Миткевичем (рис. 1). Работа схемы описывается далее.
Рис. 1. 3. Основные особенности импульсного метода регулирования Регулирование напряжения потребителя посредством импульсных преобразователей (ИП) называют импульсным регулированием. С помощью импульсного преобразователя источник постоянного или переменного напряжения периодически подключается к нагрузке. Преобразователи, позволяющие осуществлять широтно-импульсное регулирование напряжения на нагрузке, называют широтно-импульсными преобразователями (ШИП). ШИП находят широкое применение для регулирования и стабилизации напряжения различных потребителей (электротранспорт, электропривод металлообрабатывающих станков, в бортовых системах и т.д.), что объясняется рядом их преимуществ: · высокий к.п.д., так как потери мощности на регулирующем элементе преобразователя незначительны по сравнению с потерями мощности в случае непрерывного регулирования; · малая чувствительность к изменениям температуры окружающей среды, поскольку регулирующим фактором является время проводимости ключа, а не величина внутреннего сопротивления регулирующего элемента, что имеет место при непрерывном регулировании; · малые габариты и масса; · постоянная готовность к работе. Вместе с тем широтно-импульсным преобразователям присущи и недостатки: · импульсный режим работы регулирующего элемента приводит к необходимости устанавливать выходные фильтры, что вызывает инерционность процесса регулирования в замкнутых системах; · высокие скорости включения и выключения тока в силовой цепи ШИП приводит к возникновению радиопомех. Несмотря на указанные недостатки, применение импульсных преобразователей перспективно в тех случаях, когда на первое место выдвигаются требования высокой экономичности, надежности, малых габаритов, малой чувствительности к колебаниям температуры, высокой гибкости и точности регулирования. Выходные каскады ШИП наиболее просто выполнять на полностью управляемых вентилях — транзисторах и двухоперационных тиристорах, отпирание и запирание которых производится по базовым цепям. 4. Описание работы схемы Электрические параметры определяются в общем виде для многофазного выпрямителя с числом пульсаций выпрямленного напряжения за период При активно-индуктивной нагрузке ( При учете индуктивностей рассеяния обмоток трансформатора
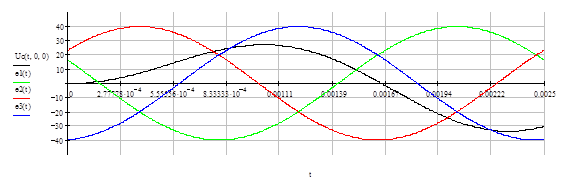
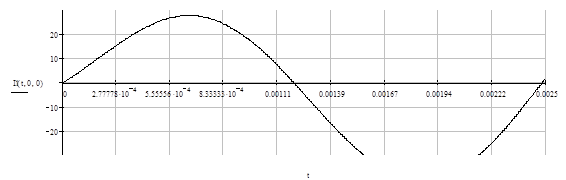
Рис. 2. Рассмотрим режим, соответствующий двум интервалам периода — интервалу одиночной работы вентиля, когда ток в вентиле равен току нагрузки В период коммутации анализ схемы удобно производить методом наложения действий источников синусоидальных э.д.с. вторичных обмоток трансформатора и источника постоянного тока Временные диаграммы токов и напряжений в трехфазном управляемом выпрямителе с нулевым выводом при активно-индуктивной нагрузке ( 5. По структурной схеме На входе схемы стоит трансформатор для понижения сетевого напряжения. Напряжение с трансформатора подается на управляемые вентили, где выпрямляется и фильтруется фильтром, а затем выпрямленное поступает к нагрузке. Стабилизация происходит за счет регулирования угла отпирания вентилей. Сигналы для отпирания тиристоров приходят с системы управления (СУ), для нашего случая можно использовать оптотиристоры или трансформатор для гальванической развязки СУ и силовой части. Система синхронизации согласована с частотой сети. 6. Расчет силовой части Расчет основных соотношений: Определяем
Определяем коэффициенты изменения питающего напряжения:
Зададимся падением напряжения на элементах схемы: · на активном сопротивлении трансформатора: · на вентилях: · на активном сопротивлении дросселя: Определим максимальное и минимальное требуемое выпрямленное напряжение
Уравнение нагрузочной характеристики имеет вид:
При минимальном напряжении сети и максимальном напряжении на нагрузке будет справедливо:
Зададимся минимальным углом управления
Определим номинальное и максимальное значения напряжений на фазной обмотке:
Зная максимальное напряжение на фазной обмотке, определим максимальный угол управления:
Определим номинальный угол управления:
Из полученных значений для углов регулирования следует, что возможна робота нулевого диода. Определим максимальные и минимальные токи нагрузки:
Расчет основных параметров вентилей: Максимальный ток через вентили:
Максимальный ток через нулевой диод:
Максимальное обратное напряжение на тиристорах
Максимальное обратное напряжение на нулевом диоде:
Выбираем следующие элементы с [2]: Диод: 50WQ06FN с параметрами: максимальный средний ток Тиристоры: 10R1A10 с параметрами: максимальный средний ток По вольт-амперным характеристикам элементов определяем сопротивления элементов в открытых состояниях:
Расчет трансформатора: Определим коэффициент трансформации
Определяем габаритную мощность трансформатора:
Определяем активное сопротивление трансформатора
где
Определяем Определяем
Определим
Определим
Как видим сопротивление трансформатора меньше принятого нами. Максимальное значение токов первичной и вторичной обмоток трансформатора:
Расчет фильтра: Определим необходимый коэффициент сглаживания индуктивно-емкостного фильтра по формуле
Для нашего случая
При коэффициенте сглаживания Поскольку у нас Коэффициент сглаживания индуктивно-емкостного фильтра можно определить как:
Определим произведение
Подставим числовые значения:
Индуктивность дросселя определим из условия непрерывности тока в нем:
Подставим числовые значения:
Выбираем дроссель с [4]: Дроссель типа IHV с параметрами: индуктивность дросселя – 500мкГн, разброс номинала Падение напряжения на дросселе:
Как видим это значение близко к принятому. Емкость конденсатора фильтра:
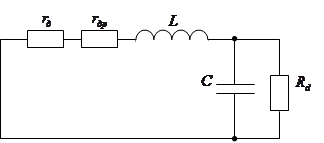
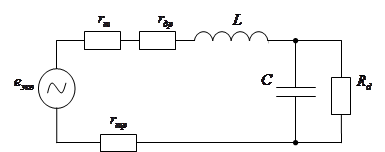
Выбираем конденсатор с [4]: Конденсатор типа 021ASM с параметрами: емкость конденсатора — 470мкФ, разброс номинала 7. Расчет переходного процесса Поскольку происходит коммутация тиристоров, то для расчета переходного процесса, заменяем нашу схему двумя эквивалентными, которые соответствуют двум интервалам работы схемы: Элементы: трансформатор, тиристоры и диод заменяем моделями. Эквивалентные схемы для двух периодов имеют вид: 1)
Где: Представим сумму сопротивлений Схема примет вид:
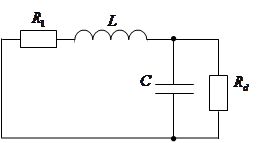
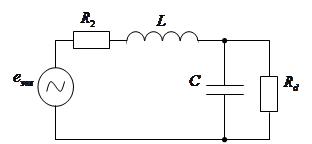
2)
Где: Представим сумму сопротивлений Схема примет вид:
8. Определение функции описывающие переходной процесс Определим функции описывающие переходной процесс для двух периодов. Используем операторный метод. Определим значение
Определим значение
Для закона ома в операторной форме справедлива запись:
Но эта запись закона Ома справедлива для расчета переходного процесса в цепи при нулевых начальных условиях. Если же начальные условия не нулевые, форма записи закона Ома в операторной форме будет иметь вид:
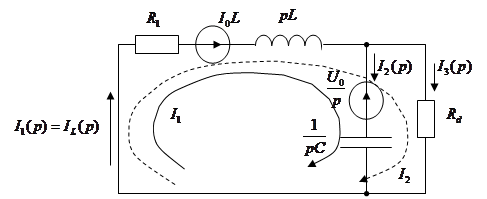
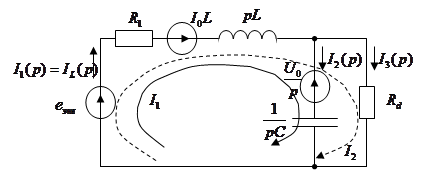
где Составим схемы замещения и запишем уравнения описывающие переходной процесс с учетом начальных условиях (при нулевых начальных условиях Для периода
Используя метод контурных токов, составим систему уравнений:
Представим это в виде:
где
9. Нахождение выражения для тока Определим
Подставляем полученное выражение в первое уравнение системы (2):
Получаем выражение
Поскольку
Подставляя найденные выражения в (3), получим выражение тока
Нахождение выражения для тока Определим
Подставляем полученное выражение в первое уравнение системы (2):
Получаем выражение
Поскольку
Подставляя найденные выражения в (5), получим выражение тока
Определяем значения токов в ветвях
Определим напряжение на емкости
10. Обратные изображения для Лапласа Обратные изображения Лапласа для
Для периода
Представим это в виде:
где
Нахождение выражения для тока Определим
Подставляем полученное выражение в первое уравнение системы (2):
Получаем выражение
Поскольку
Подставляя найденные выражения в (3), получим выражение тока
Нахождение выражения для тока Определим
Подставляем полученное выражение в первое уравнение системы (2):
Получаем выражение
Поскольку
Подставляя найденные выражения в (5), получим выражение тока
Определяем значения токов в ветвях
Определим напряжение на емкости
11. Обратные изображения для Лапласа Обратные изображения Лапласа для
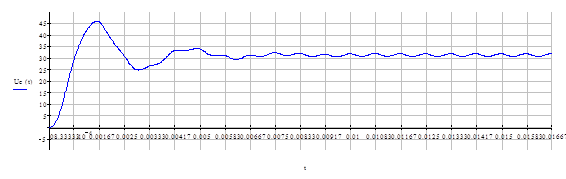
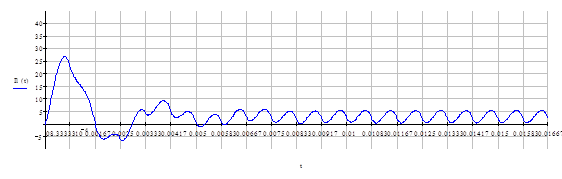
Построим графики этих функция для при нулевых начальных условиях
Определяя значения функций в точке
При нагрузке
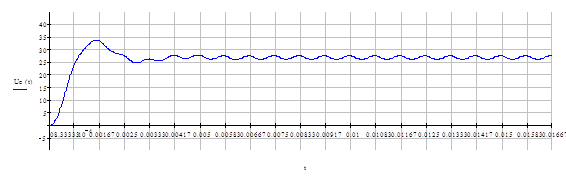
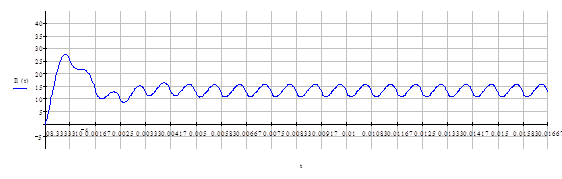
Составим таблицу (табл.. №1) значений токов (ток в дросселе) и напряжений (напряжение в конденсаторе) для двух нагрузок: минимальной Таблица №1
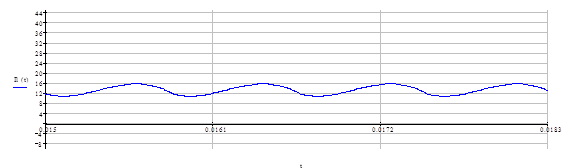
Как видим, процесс стал полностью периодичен при минимальной нагрузке с 16 такта Отсюда следует вывод, что установившийся режим мы получаем за время близкое к 0.02с. Рассмотрим установившийся режим при минимальной нагрузке
Список использованной литературы 1. Руденко В.С., Сенько В.И., Чиженко И.М. — 2-е изд., пере раб. и доп. — Вища школа. Головное изд-во, 1983. — 431с. 2. Электронный справочник InternationalRectifier. 3. В.Е. Китаев, А.А. Бокуеяев. — Расчет источников электропитания устройств связи. — М.: Связь, 1979. —216с. 4. Интернет страничка: www.vishay.com. 5. Ромашко В.Я. — Основи аналізу дискретно-лінійних ланцюгів: Навч. Посібник. — К.: Либідь, 1993. — 120с. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
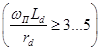 . Для
. Для 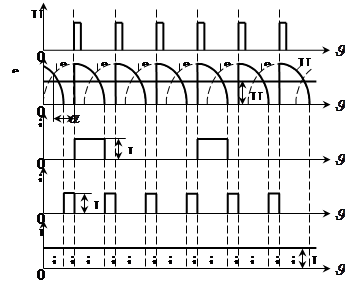
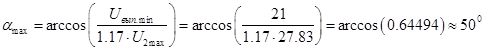 .
.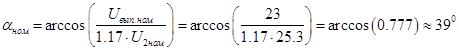 .
.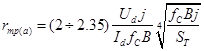 ;
;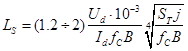 .
.
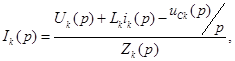
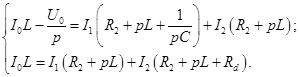 (1)
(1)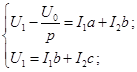 (2)
(2)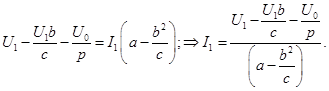
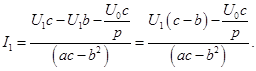 (3)
(3)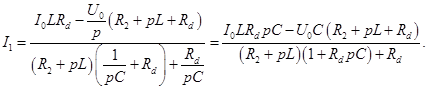
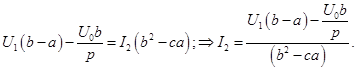
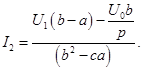 (5)
(5)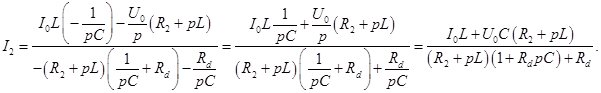
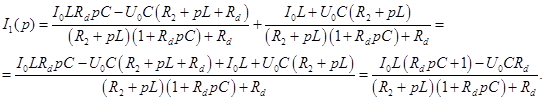
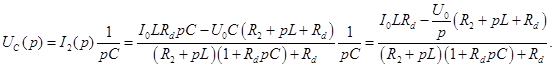
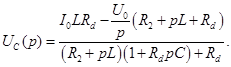
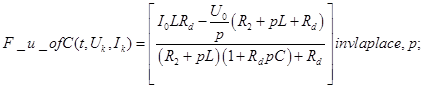
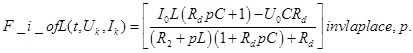
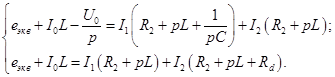 (1)
(1)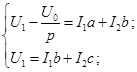 (2)
(2)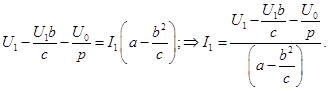
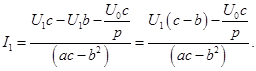 (3)
(3)