По территориям Волго-Вятского, Центрально-Черноземного и Поволжского районов известны данные за ноябрь 1998 г.
| Район |
Потребительские расходы в расчете на душу населения тыс. руб. у |
Средняя заработная плата и выплаты социального характера, тыс. руб., х |
| Волго-Вятский район
|
| Респ. Марий Эл |
302 |
554 |
| Респ. Мордовия |
360 |
560 |
| Чувашская респ. |
310 |
545 |
| Кировская обл. |
415 |
672 |
| Нижегородская обл. |
452 |
496 |
| Центрально-Черноземный
|
| Белгородская обл. |
502 |
777 |
| Воронежская обл. |
355 |
632 |
| Курская обл. |
416 |
688 |
| Липецкая обл. |
501 |
833 |
| Тамбовская обл. |
403 |
577 |
| Поволжский
|
| Респ. Калмыкия |
208 |
584 |
| Респ. Татарстан |
462 |
949 |
| Астраханскаяобл. |
368 |
888 |
| Волгоградская обл. |
399 |
831 |
| Пензенская обл. |
342 |
562 |
| Саратовская обл. |
354 |
665 |
| Ульяновская обл. |
558 |
705 |
Задание
1. Постройте поле корреляции и сформируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнений линейной, степенной, экспоненциальной, обратной, гиперболической парной регрессии.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Рассчитайте коэффициент эластичности.
5. Оцените качество уравнений с помощью средней ошибки аппроксимации.
6. Оцените статистическую надежность результатов регрессионного моделирования с помощью F-критерия Фишера. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выберите лучшее уравнение регрессии и дайте его обоснование.
7. Рассчитайте ожидаемое значение результата, если прогнозное значение фактора увеличится на 7% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости a=0,05.
8. Оцените полученные результаты.
Построим поле корреляции:
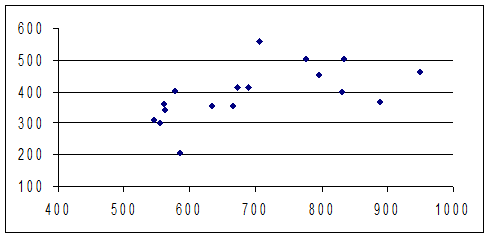
В данном случае можно сформулировать гипотезу о наличии связи между расходами и заработной платы, носящей скорее всего гиперболический характер.
1.1 Построить линейную модель.
Определим линейный коэффициент парной корреляции по следующей формуле, используя данные таблицы 1 приложения.Можно сказать, что связь между размером потребительских расходов и средней заработной платы и выплат социального характера.
Уравнение линейной регрессии имеет вид: Значения параметров линейной модели определим, используя данные таблицы 1.
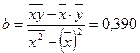 , , 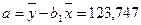 . .
Уравнение регрессии имеет вид: Рассчитаем коэффициент детерминации:
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера.

F> Fтабл=4,54 для α=0,05; k1
=m=1;k2
=n-m-1=15, то уравнение регрессии с вероятностью 0,95 в целом статистически значимое.
Определим среднюю ошибку:
В среднем расчетные значения ý для линейной модели отличаются от фактических значений на 4,04%.
1.2 Построение степенной модели парной регрессии
Уравнение степенной регрессии имеет вид:

Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
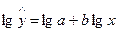
Данные приведены в таблице 2 приложения.
Обозначим Y=lgŷ, X=lgx, A=lga.
Тогда уравнение примет вид: Y=A+bX-линейное уравнение регрессии. Рассчитаем его параметры, используя данные таблицы 3.
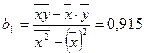
A=0,001
Уравнение регрессии будет иметь вид: Y=0,001+0,915X
Перейдем к исходным данным уравнения, выполнив потенциирование данного уравнения:
Ŷ=10-0,001
*х0,915
Получим уравнение степенной модели регрессии: Ŷ=0,998*х0,915
Определим индекс корреляции:

Связь между показателем у и фактором х можно считать достаточно сильной. Коэффицент детерминации равен R2
=r2
XY
=0,728
Рассчитаем критерий Фишера.
F> Fтабл=4,54 для α=0,05; k1
=m=1;k2
=n-m-1=15Средняя относительная ошибка
В среднем расчетные значения ý для степенной модели отличаются от фактических значений на 1,28%.1.3 Построение экспоненциальной функции
Ŷ=аbx
Для построения этой модели необходимо провести линериаризацию переменных. Для этого осуществим логарифмирование обеих частей уравнения.
Lgŷ=lga+xlgb
Обозначим Y=lgŷ, B=lgb, A=lga
Получим линейное уравнение регрессии:
Y=A+Bx
Рассчитаем его параметры, используя данные таблицы 4 приложения.
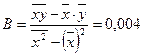 , ,  . .
Перейдем к исходным данным уравнения, выполнив потенциирование данного уравнения:
Ŷ=100,026
*(100,004
)x
=1,06*1,01x
Определим индекс корреляции:Связь между показателем у и фактором х можно считать недостаточно сильной. Коэффицент детерминации равен R2
=r2
XY
=0,404
Рассчитаем критерий Фишера.F<Fтабл=4,54 для α=0,05; k1
=m=1;k2
=n-m-1=15
Уравнение регрессии с вероятностью 0,95 в целом статистически значимое, т.к. F> Fтабл.Средняя относительная ошибка
В среднем расчетные значения ý для экпоненциальной модели отличаются от фактических значений на 5,16%.
1.4 Построение гиперболической функции
Уравнение гиперболической функции:
Ŷ=a+b/x
Проведем линеаризацию модели путем замены Х=1/х. В результате получим линейное уравнение ŷ=a+bX
Рассчитаем его параметры по данным таблицы 5.
 , , 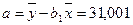 . .
Получим следующее уравнение гиперболической модели:
Ŷ=31,001+215709,49/х
Определим индекс детерминации:r2
=0,951
Вариация результата Y на 95,1% объясняется вариацией фактора Х.
Рассчитаем критерий Фишера.F>Fтабл=4,54 для α=0,05; k1
=m=1;k2
=n-m-1=15
Средняя относительная ошибка: 0,067*44,106=2,955%
В среднем расчетные значения ý для гиперболической модели отличаются от фактических значений на 2,955%.
1.5 Выбор лучшей модели
Для выбора лучшей модели построим сводную таблицу результатов
| Коэффициент детерминации |
F-критерий Фишера |
Индекс корреляции |
Средняя относительная ошибка |
| Линейная |
0,346 |
7,9 |
0,588 |
4,04 |
| Степенная |
0,728 |
40,2 |
0,924 |
1,28 |
| Экспоненциальная |
0,636 |
0,404 |
10,17 |
5,16 |
| Гиперболическая |
0,951 |
291,1 |
0,975 |
2,955 |
Наибольшее значение коэффициента детерминации и критерия Фишера имеет гиперболическая модель. Она же имеет практически наименьшую среднюю относительную ошибку, значит, ее можно взять в качестве лучшей для построения прогноза.
1.6 Расчет прогнозного значения результативного показателя.
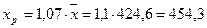 . .
Подставим значение xр
в уравнение гиперболической регрессии:
Ŷ=31,001+215709,49/х

Доверительный интервал прогноза для уровня значимости a
определяется в виде:
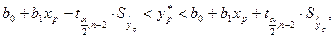
где

Рассчитаем необходимые величины:
 ; ;
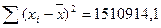
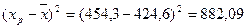 ; ;
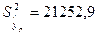 ; ; 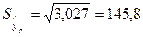 ; ;
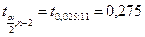 . .
В результате доверительный интервал прогноза для уровня значимости 0,05 равен:
505,8-0,275*145,8 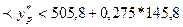 . .
465,7
8. Полученные результаты, в целом удовлетворительные. Модель гиперболической парной регрессии описывает реальную зависимость рассматриваемыми показателями.
|