ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА САМОДИФФУЗИИ МЕТОДОМ ХАНА С ПОСТОЯННЫМ ГРАДИЕНТОМ МАГНИТНОГО ПОЛЯ
В настоящее время наиболее уникальным и информативным методом изучения структуры и свойств веществ является метод ядерного магнитного резонанса (ЯМР).Суть метода основана на явлении резонансного поглощения ядрами со спином 1/2, находящихся в магнитном поле Но
(спиновой системой), энергии радиочастотного поля Н1
, с последующим высвобождением этой энергии после прекращения действия поля Н1
.
Находясь в поле Но
спиновая система создает макроскопическую намагниченность М направленную вдоль этого поля. Если воздействовав на такую систему внешним переменным магнитным полем Н1
, перпендикулярным полю Но
, то макроскопическая намагниченность будет поворачиваться вокруг поля Н1
.Если за время действия поля Н1
М поворачивается на 90 градусов,то такой импульс называется 90 градусным,если поворот осуществляется на 180 градусов- это 180 градусный импульс.После прекращения действия поля Н1
спиновая система оказывается в неравновесном состоянии.Восстановление к равновесному состоянию характеризуются процессами релаксации, с характеристическими временами Т1
-временем спин-решеточной (продольной) релаксации, Т2
-временем спин-спиновой (поперечной) релаксации.
Построение спектрометров ЯМР таково, что в них регистрируется сигнал наведенный в приемо-передающей катушке, ось которой перпендикулярна полю Но
,компонентой макроскопической намагниченности Мху
, лежащей в плоскости ху, перпендикулярной полю Но
.Интенсивность А этого сигнала пропорциональна величине Мху
.После 90 градусного импульса величина А,в процессе релаксации, изменяется от максимального значения до нуля. Это изменение называется спадом свободной индукции (ССИ) .
Для измерения времени спин-спиновой релаксации Хан предложил на спиновую систему воздействовать импульсной последовательностью 90-t-180 (последовательность Хана).В момент времени 2t после начала 90 градусного импульса формируется, так называемое, спиновое эхо (рис.1).
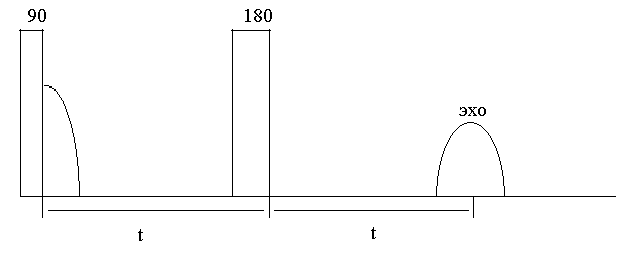 Рисунок 1. Рисунок 1.
Зависимость амплитуды спинового эхо от интервала t в последовательности Хана описывается выражением:
А(t)=Aо
exp(-2t/T2
) (1)
Aо
- начальная амплитуда ССИ; А(t) амплитуда спинового эхо, t- интервал времени между 90-гр. и 180-гр. импульсами.
Метод Хана позволяет определить значение Т2
только в том случае, когда за время 2t молекулы не перемещаются. Однако, как известно, молекулы в жидкости находятся в состоянии непрерывного теплового движения. Такое движение молекул называется самодиффузией и характеризуется коэффициентом самодиффузии D, который численно равен среднеквадратичному смещению <r2
> которое испытывает молекула за время диффузии td
:
D=<r2
>/6td
(2)
Поэтому, реально с учетом релаксационного и диффузионного вкладов, амплитуда эхо будет описываться выражением:
А(t)=Ao
exp(-2t/T2
) exp[-(2/3)g2
g2
t3
D] (3)
где: g - гиромагнитное отношение; g - градиент внешнего магнитного поля;
в - коэффициент самодиффузии,
Для уменьшения влияния самодиффузии Карр и Парселл модифицировали последовательность Хана в многоимпульсную последовательность 90-t-180-2t-180-2t-180-..., (последовательность Карра-Парселла). Эта последовательность позволяет получить серию эхо, которые формируются в промежутках между 180 градусными импульсами. Огибающая эхо в последовательности Карра-Парселла представляет собой релаксационное затухание и описывается выражением:
А(t)=Ao
exp(-t/T2
) exp[-(2/3)g2
g2
t2
Dt] (4)
где А(t) -амплитуда эхо в момент времени t.
Из выражения (4) видно, что выбирая t достаточно малымэкспоненциальным множителем, учитывающим влияние самодиффузии,можно пренебречь. В этом случае огибающая эхо будет определяться тольколишь процессами спин-спиновой релаксации и описываться выражением:
А(t)/Ао
=ехр(-t/Т2
) (5)
Логарифмируя последнее выражение получим:
ln[A(t)/Ао
]= - t/Т2
(6).
Если Ао
/А(t)=е- основанию натурального логарифма, то ln(Ао
/А(t))=1. Тогда по наклону зависимости ln(А(t)/Ао
)=f(t) легко определить время Т2
,поскольку, в этом случае, tе
=Т2
, где tе
- время, в течении которого амплитуда эхо уменьшается в е раз (рис.2а).
Как было отмечено выше, амплитуда спинового эхо в методе Хана определяется как временем спин-спиновой релаксации Т2
, так и коэффициентом самодиффузии D. Поэтому этот метод может быть использован для измерения коэффициента самодиффузии. Из выражения (3) видим, что амплитуда эхо зависит от градиента внешнего магнитного поля g и от времени t между 90 и 180 градусными импульсами.
Экспериментальное измерение коэффициента самодиффузии заключается в получении диффузионного затухания спинового эхо. Для этого зафиксировав наиболее удобный интервал t, и оставляя его постоянным, получают затухание спинового эхо в зависимости от величины градиента магнитного поля g. Согласно выражению (3) отношения амплитуд спинового эхо при различных градиентах магнитного поля определится:
А(g)/A(gо
) =ехр [-2/3 g2
(g2
-gо
2
) t3
D] (7)
где А(g) - амплитуда эхо при градиенте g, А(gо
) - амплитуда эхо при естественном градиенте gо
.
Логарифмируя выражение (7), и полагая величину естественного градиента go
<<g, получим:
ln[A(g)/А(go
)]= -(2/3) g2
g2
t3
D (8)
Если A(gо
)/А(g)=е, то согласно (8) имеем:
D=3/2g2
t3
ge
2
(9)
где gе
- величина градиента, при котором амплитуда спинового эхо уменьшается в е раз.
Экспериментально для определения коэффициента самодиффузии строят зависимость ln[А(g)/А(gо
) =f(g).Найдя затухание амплитудыэхо в е раз, и определив gе
, по выражению (9) вычисляют коэффициент самодиффузии в (рис. 2б).
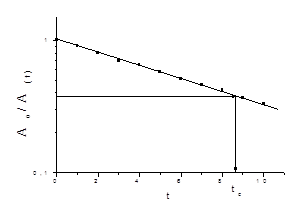 а) а) |
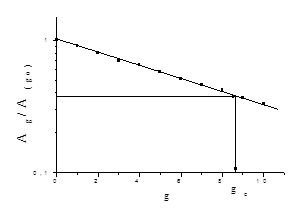 б) б) |
| Рисунок 2.
|
Список литературы
1. Фаррар Т., Беккер Э. Импульсная и Фурье спектроскопия ЯМР.- М. :Мир, 1973.
2. Вашман А.А.,Пронин И.С. Ядерная магнитная релаксация и ее применение в химической физике. - М. :Наука, 1979.
3. Маклаковский А.И., Скирда В.Д., Фаткулин Н.Ф. Самодиффузия в растворах и расплавах полимеров. - Казань. :Изд-во Казанского университета, 1987.
4. Курс лекций по спецкурсу ЯМР.
|