МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (МАИ)
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет «СИСТЕМЫ УПРАВЛЕНИЯ, ИНФОРМАТИКА И ЭЛЕКТРОЭНЕРГЕТИКА»
Кафедра 308 «Информационные технологии»
Пояснительная записка к курсовой работе
по дисциплине: «Теория чисел»
Выполнил: Тузов И.И.
Группа 03-119
Руководитель: доцент, к.т.н. Гридин А.Н.
Москва 2010
Оглавление
Задание
Оглавление
Введение
1. Интерфейс программы
2. Описание процедур
2.1 DelOstatok
2.2 Factor
2.3 NodNok
2.4 SuperGorner
2.5 Express
2.6 AntiExp
Заключение
Список использованных источников
Приложение
Листинг программы
Задание
Разработать программу-калькулятор CalcKurs на языке программирования Pascal, реализующую следующие функции:
1.формирование заданного подмножества натурального ряда с помощью общего делителя;
2.факторизация числа с опциями;
3.нахождение НОД и НОК для заданной совокупности натурального ряда;
4.нахождение рациональных решений уравнения с целочисленными коэффициентами;
5.представление рациональной дроби в виде цепной;
6.представление цепной дроби в виде рациональной.
Оборудование и ПО:
Название Windows: Windows Seven (6.1.7600) Ultimate
Название процессора: Intel(R) Core(TM)2 CPU 6300 @ 1.86GHz
Установлено памяти: 1 022,49 MB
Среда программирования: Turbo Pascal 7.0
Введение
Теория чисел — это одно из направлений математики, которое иногда называют «высшей арифметикой». Данная наука изучает натуральные числа и некоторые сходные с ними объекты, рассматривает различные свойства (делимость, разложимость, взаимосвязи и так далее), алгоритмы поиска чисел, а также определяет ряд достаточно интересных наборов натуральных чисел.
Так, к примеру, в рамках теории чисел рассматриваются вопросы делимости целых чисел друг на друга, алгоритм Евклида для поиска наибольшего общего делителя, поиск наименьшего общего кратного, малая и большая теоремы Ферма. В качестве самых известных рядов натуральных чисел можно привести ряд Фибоначчи, простые числа, совершенные и дружественные числа, степени и суперстепени натуральных чисел.[1]
Вне самой математики теория чисел имеет довольно мало приложений, и развивалась она не ради решения прикладных задач, а как искусство ради искусства, обладающее своей внутренней красотой, тонкостью и трудностью. Тем не менее теория чисел оказала большое влияние на математическую науку, поскольку некоторые разделы математики (в том числе и такие, которые впоследствии нашли применение в физике) были первоначально созданы для решения особенно сложных проблем теории чисел.[2]
Разработанная программа включает в себя набор из нескольких основных операций, которые могут понадобиться при решении более сложных задач.
Назначение программы CalcKurs.
Программа CalcKurs выполняет следующие функции:
1.формирование заданного подмножества натурального ряда с помощью общего делителя;
2.факторизация числа с опциями;
3.нахождение НОД и НОК для заданной совокупности натурального ряда;
4.нахождение рациональных решений уравнения с целочисленными коэффициентами;
5.представление рациональной дроби в виде цепной;
6.представление цепной дроби в виде рациональной.
1. Интерфейс программы


2. Описание процедур
2.1 DelOstatok
Назначение.
Данная процедура формирует заданное подмножество натурального ряда с помощью общего делителя.
Алгоритм.
Ищется общий делитель совокупности делителей (общий делитель ищется с помощью нахождения наименьшего общего кратного делителей). На заданном множестве (кол-во цифр в числах) ищем первый элемент, который будет удовлетворять заданному условию (делится на НОК с остатком), запоминаем элемент и прерываем цикл.
Формируем подмножество с помощью прибавления к первому элементу делителя, суммируем количество элементов, пока элементы не станут больше заданной размерности.
Пример.
Делитель=10, остаток=3, размерность=2 (от 10 до 99)
Количество элементов=9
Подмножество элементов={13, 23, 33, 43, 53, 63, 73, 83, 93}
Тесты.
1.Некорректные данные

2.Корректные данные

2.2 Factor
Назначение.
Данная процедура выполняет факторизацию (разложение на простые множители) числа с опциями.
Алгоритм.
Ищем для данного числа простой множитель с помощью решета Эратосфена[3] (Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
Пусть переменная p изначально равна двум — первому простому числу.
Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …)
Найти первое не вычеркнутое число, большее чем p, и присвоить значению переменной p это число.
Повторять шаги 3 и 4 до тех пор, пока p не станет больше, чем n
Все не вычеркнутые числа в списке — простые числа.)
и делим заданное число на данный множитель, потом ищем следующий простой множитель(если он повторяется, то возводим его в степень), и так до тех пор, пока число не станет равным единице. Записываем все простые множители.
Далее находим все делители числа и составляем из них множество. Вычисляем сумму делителей.
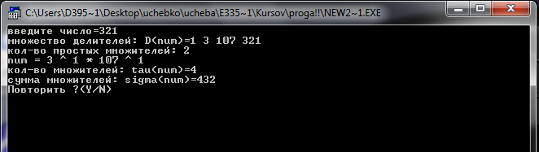
Пример.
Число=21
множество делителей=1 3 7 21
кол-во простых множителей=2
21=3 ^ 1 * 7 ^ 1
кол-во множителей=4
сумма множителей=32
Тесты.
1.Некорректные данные

2.Корректные данные
2.3 NodNok
Назначение.
Данная процедура находит НОД и НОК для заданной совокупности натурального ряда.
Алгоритм.
С помощью алгоритма Евклида (есть числа a,b и последовательность R1>R2>R3>…>RN, где каждое RK - это остаток от деления предпредыдущего числа на предыдущее, а предпоследнее делится на последнее нацело. Тогда НОД(a,b), наибольший общий делитель a и b, равен RN, последнему ненулевому члену этой последовательности) находим НОД[4] для первых двух чисел, «цепляем» следующее число для нахождения следующего НОД, и так до тех пор, пока совокупность чисел не закончится.
Для нахождения НОК первых двух чисел используем следующий алгоритм: разлагаем данные числа на простые множители и к одному из таких разложений приписываем множители недостающие у него против разложений остальных данных чисел[5], и аналогично нахождению НОД «цепляем» следующее число.
Пример.
Числа: 21 и 12
НОД(12,21)=3
НОК(12,21)=84
Тесты.
1.Некорректные данные

2.Корректные данные

2.4 SuperGorner
Назначение.
Данная процедура находит рациональные решения уравнения с целочисленными коэффициентами.
Алгоритм.
Рациональные корни уравнения ищутся с помощью расширенной схемы(метода) Горнера[6] (раскладываем свободный член и коэффициент перед старшей степенью на все возможные множители и делим все множители свободного члена на все множители коэффициента перед старшей степенью (добавляем также знак “-”); подставляем полученные значения в уравнение, если уравнение получается равным нулю, то это значение – корень данного уравнения).
Пример.
Уравнение: 6x3-11x2+6x-1=0
Возможные корни: +1, +1/2, +1/3, +1/6
Корни уравнения: 1/3, 1/2, 1
Тесты.
1.Некорректные данные

2.Корректные данные

2.5 Express
Назначение.
Данная процедура переводит рациональную дробь в цепную[7].
Алгоритм.
Делим числитель на знаменатель, запоминаем его целое значение (a div b, где а – числитель, b - знаменатель), находим остаток от деления числителя на знаменатель (a mod b), присваиваем числителю значение остатка, меняем местами числитель и знаменатель, и так делаем до тех пор, пока (a mod b) не станет равен нулю.
Пример.
Рациональная дробь:123/47
Цепная дробь: [2,1,1,1,1,1,1,3]
Тесты.
1.Некорректные данные

2.Корректные данные

2.6 AntiExp
Назначение.
Данная процедура переводит цепную дробь в рациональную.
Алгоритм.
Умножаем последний элемент цепной дроби с предпоследним и прибавляем к полученному значению единицу, это будет значением числителя, значением знаменателя будет последний элемент цепной дроби, меняем их местами, теперь последним элементом цепной дроби будет полученный знаменатель; так делаем, пока не закончатся элементы цепной дроби.
Пример.
Цепная дробь: [2,3,4,5]
Рациональная дробь: 157/68
Тесты.
1.Некорректные данные

2.Корректные данные

Заключение
Разработана программа CalcKurs, выполняющая следующие функции:
1.формирование заданного подмножества натурального ряда с помощью общего делителя;
2.факторизация числа с опциями;
3.нахождение НОД и НОК для заданной совокупности натурального ряда;
4.нахождение рациональных решений уравнения с целочисленными коэффициентами;
5.представление рациональной дроби в виде цепной;
6.представление цепной дроби в виде рациональной.
К минусам программы можно отнести невысокую размерность чисел, которые участвуют в вычислениях (-2147483648..2147483647), некоторые алгоритмы можно сделать более оптимальными.
К плюсам можно отнести простоту в пользовании программой, её малую требовательность к ресурсам компьютера, программа исполняет основополагающие алгоритмы теории чисел. Она может помочь в изучении данного раздела математики.
Список использованных источников
1. http://ru.wikipedia.org/wiki/Теория_чисел
2. http://www.krugosvet.ru/enc/nauka_i_tehnika/matematika/CHISEL_TEORIYA.html
3. http://ru.wikipedia.org/wiki/Решето_Эратосфена
4. http://ru.wikipedia.org/wiki/Наибольший_общий_делитель
5. http://ru.wikipedia.org/wiki/Наименьшее_общее_кратное
6. http://ru.wikipedia.org/wiki/Метод_Горнера
7. http://dic.academic.ru/dic.nsf/es/39322/непрерывная
Приложение
Листинг программы
program kurs;
uses crt;
function pow(a,x:longint):longint;
var
t,i:longint;
begin
t:=a;
for i:=1 to x-1 do
t:=t*a;
pow:=t;
end; {pow}
{----------------------------------------}
procedure DelOstatok;
var
dd:array [1..200] of integer;
R:integer; {размерность чисел}
i:longint; {делитель}
k:longint; {остаток}
D,a,b:longint; {элементы заданного множества}
SUM:longint; {кол-во эл-ов, удовл условию}
S,T:byte;
q:char;
e,j,l,n:integer;
maxa,minj,maxj:longint;
begin
repeat
begin
writeln('введите ко-во чисел для нахождения НОК делителей');
readln(n);
writeln('введите ',n,' чисел: ');
readln(dd[1]);
maxa:=dd[1];
for i:=2 to n do
begin
readln(dd[i]);
if dd[i]>maxa then maxa:=dd[i];
end;
i:=1;while (dd[i]<>0) and (i<=n) do inc(i);
if i<>n+1 then writeln('НОК не сущ-ет')
else begin
e:=1;
for i:=2 to maxa do
begin
maxj:=0;
for l:=1 to n do
begin
j:=0;
while (dd[l] mod i=0) do
begin
dd[l]:=dd[l] div i;
inc(j);
end;
if (j>maxj) then maxj:=j;
end;
if (maxj<>0) then for l:=1 to maxj do e:=e*i;
end;
writeln('НОК делителей=',e);
end;
end;
i:=e;
write ('введите остаток=');
readln(k);
if ((i<=0) or (k<0)) then {проверка
{вывод эл-ов на экран}
end; writeln;
end;
writeln('Повторить ?(Y/N)');
q:=ReadKey;
until q in ['N','n'];
clrscr;
end; {DelOstatok}
{----------------------------------------}
procedure Factor;
var
numb, powers: array [1..100] of longint;
c:longint;
n:longint;
n1,H:longint;
i:longint;
k,t: longint;
q:char;
begin
repeat
write('Введите число=');
readln(c);
if c<=0 then {проверка на корр числа}
begin
writeln('число должно быть>0');
readln;
exit;
end
else
{вывод мн-ва делителей}
begin
write('мн-во делителей: D(num)=');
for H:= 1 to c do
if c mod H=0 then
write(H,' ');
end;
{конец вывода делителей}
n:= 1;
n1:= 0;
while c <> 1 do
begin
i:= 2;
while c mod i <> 0 do {проверка на делимостьс/без остатка}
Inc(i);
Inc(n1);
if n1 = 1 then
begin
numb[n]:= i;
powers[n]:= 1;
end
else
if numb[n] = i then Inc(powers[n])
else
begin
Inc(n); {увеличение кол-ва простых множителей}
numb[n]:= i;
powers[n]:= 1;
end; {while}
c:= c div i; {деление числа на простой множитель}
end; {while}
{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}
writeln;
writeln('кол-во простых множителей: ',n);
write('num = ');
k:=1;
t:=1;
writeln('НОД=',k);
if k=1 then writeln('числа взаимно простые');
end;
begin
i:=1;while (b[i]<>0) and (i<=n) do inc(i);
if i<>n+1 then writeln('НОК не сущ-ет')
else begin
d:=1;
for i:=2 to maxa do
begin
maxj:=0;
for l:=1 to n do
begin
j:=0;
while (b[l] mod i=0) do
begin
b[l]:=b[l] div i;
inc(j);
end;
if (j>maxj) then maxj:=j;
end;
if (maxj<>0) then for l:=1 to maxj do d:=d*i;
end;
writeln('НОК=',d);
end;
end;
end;
writeln('Повторить ?(Y/N)');
q:=ReadKey;
until q in ['N','n'];
clrscr;
end;{NodNok}
{----------------------------------------}
procedure SuperGorner;
type
vector= array[1..11] of integer;
rvector=array[1..100] of real;
var
sum,suma:real;
i,k,j,b,c,a,n:integer;
vec:vector;
vecb:rvector;
veca:rvector;
q:char;
BEGIN
Writeln('Введите степень уравнения (max = 10)');
Readln(n);
if n<=0 then writeln(‘степень не может быть<=0’)
else begin
Inc(n);
writeln('введите его коэффициенты:');
for i := 1 to n do
read(vec[i]);
while vec[i]=0 do
Begin
i:=i-1;
writeln('ответ:0');
End;
k:=1;
b:=vec[i];
for j:=1 to abs(b) do
begin
if (b mod j)=0 then
begin
vecb[k]:=j;
k:=k+1;
procedure AntiExp;
var s: array [1..100] of integer;
a,b,i,n,t:integer;
q:char;
begin
repeat
writeln('введите кол-во эл-ов цепной дроби=');
read(n);
if n<=0 then writeln(‘кол-во эл-ов не может быть<=0’)
else begin
writeln('введите значения этих эл-ов=');
for i:=1 to n do
read(s[i]);
a:=1;b:=s[n];
for i:= n downto 2 do
begin
t:=s[i-1]*b+a;
a:=b;
b:=t;
end;
writeln;
writeln(b,'/',a);
end;
writeln('Повторить ?(Y/N)');
q:=ReadKey;
until q in ['N','n'];
clrscr;
end;{AntiExp}
{----------------------------------------}
var
k:integer;
q:char;
begin
writeln('Дискретная математика');
writeln('Курсовая работа, группа 03-119, каф308');
writeln('выполнил: Тузов И.И.');
writeln('руководитель: Гридин А.Н.');
writeln;
writeln('Калькулятор с функциями, описанными ниже');
writeln;
Writeln('Нажмите Enter');
readln;
clrscr;
repeat
writeln('Какую выполнить операцию?');
writeln;
writeln('1-вычисление мн-ва N-значных чисел с заданным делителем и остатком ');
writeln('2-факторизация числа');
writeln('3-нахождение НОД и НОК чисел');
writeln('4-нахождение рационльных корней уравнения с целочисл коэфф');
writeln('5-перевод рациональной дроби в цепную');
writeln('6-перевод цепной дроби в рациональную');
read(k);
|
делителя и остатка на отриц-сть}
begin
write ('делитель или остаток не могут быть<0 ');
end
else
begin
if i>k then {проверка на делитель>остатка}
begin
write ('введите размерность=');
readln(R);
if R<=0 then
begin
writeln ('некорректная размерность ');
readln;
end
else begin
if R=1 then
begin a:=1; b:=9; end
else begin
a:=pow(10,(R-1)); {инициализация верх и нижн границ}
b:=pow(10,R);
b:=b-1;
end;
end;
if b<i then {проверка на делимое>делителя}
writeln ('делиоме не может быть < делителя ')
else
begin
SUM:=0; {обнуление сумы кол-ва эл-ов}
for D:= a to b do
begin
if (D mod i)=k then {проверка эл-ов на условие}
begin
SUM:=SUM+1;
end;
end;
writeln;
writeln ('кол-во эл-ов с делителем=', i:3, ' и остатком=', k:3, ' равно', SUM:6);
end; {b<i}
end {if i>k}
else
write ('остаток не может быть > делителя ');
end; {if otriz}
{\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\}
write ('вывести значения на экран?(1-да\0-нет)');
readln(S);
if S=1 then
if SUM=0 then
writeln('нет эл-ов, удовл. условию')
else
begin
for D:= a to b do
if (D mod i)=k then
begin
write(' ',D:4);
{вычисление кол-ва делителей и их мн-ва}
for i:= 1 to n do
begin
write(numb[i], ' ^ ', powers[i]);
k:=k*((pow(numb[i],powers[i]+1) - 1) div (numb[i] - 1));
t:=t*(powers[i]+1); {кол-во делителей}
if i <> n then write(' * ');
end;
writeln;
writeln('кол-во множителей: tau(num)=',t);
writeln('сумма множителей: sigma(num)=',k);
writeln('Повторить ?(Y/N)');
q:=ReadKey;
until q in ['N','n'];
clrscr;
end;{Factor}
{----------------------------------------}
procedure NodNok;
type TArray=array [1..200] of integer;
var a,b:TArray;
i,l,j,maxa,minj,maxj:longint;
k,d:longint;
n:integer;
q:char;
begin
repeat
clrscr;
writeln('введите ко-во чисел для нахождения НОД и НОК');
readln(n);
writeln('введите ',n,' чисел: ');
if n<=0 then writeln(‘кол-во чисел не может быть<=0’)
else begin
readln(a[1]);
b[1]:=a[1];
maxa:=a[1];
for i:=2 to n do
begin
readln(a[i]);
b[i]:=a[i];
if a[i]>maxa then maxa:=a[i];
end;
i:=1;
while (a[i]=0) and (i<=n) do inc(i);
if i=n+1 then writeln('НОД – любое число')
else begin
for j:=1 to n do if a[j]=0 then a[j]:=a[i];
k:=1;
for i:=2 to maxa do
begin
minj:=1000;
for l:=1 to n do
begin
j:=0;
while (a[l] mod i=0) do
begin
a[l]:=a[l] div i;
inc(j);
end;
if (j<minj) then minj:=j;
end;
if (minj<>0) then for l:=1 to minj do k:=k*i;
end;
vecb[k]:=-j;
k:=k+1;
end;
end;
a:=1;
for j:=1 to abs(vec[1]) do
begin
if (vec[1] mod j)=0 then
begin
veca[a]:=j;
a:=a+1;
{ veca[a]:=-j;
a:=a+1;}
End;
end;
b:=a;
for j:=1 to k-1 do
Begin
for a:=1 to b-1 do
Begin
Begin
c:=i;
sum:=0;
for i:=1 to c do
Begin
sum:=sum+vec[i]*pow1(vecb[j]/veca[a],c-i);
if (sum<0.00001) and (sum>-0.00001) then
if vec[a]=1 then writeln('ответ:',round(vecb[j]))
else writeln('ответ:',round(vecb[j]), '/',round(veca[a]));
end;
End;
End;
End; end;
readln;
end;{SuperGorner}
{----------------------------------------}
procedure Express;
var
a,b,t:integer;
q:char;
begin
repeat
writeln('введите числитель=');
readln(a);
writeln('введите знаменатель=');
readln(b);
if b=0 then writeln(‘знаменатель не может быть=0’)
else begin
write('[');
while (a mod b>0) do
begin
write(a div b,',');
a:=a mod b;
t:=b;
b:=a;
a:=t;
end;
write(a div b, ']');
end;
writeln(‘Повторить ?(Y/N)');
q:=ReadKey;
until q in ['N','n'];
clrscr;
end;{Express}
{----------------------------------------}
case k of
1:DelOstatok;
2:Factor;
3:NodNok;
4:SuperGorner;
5:Express;
6:AntiExp;
else
writeln ('нет операции');
end;{case}
writeln('Повторить выполнение калькулятора ?(Y/N)');
q:=ReadKey;
until q in ['N','n'];
clrscr;
readln;
end.{prog}
|
|