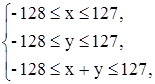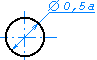Лабораторная работа: Системы счисления и представления типов данных
|
Название: Системы счисления и представления типов данных Раздел: Рефераты по информатике Тип: лабораторная работа | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Системы счисления и представления типов данных Содержание 1.Позиционные системы счисления. 3 2.Переходы между основными системами счисления. 5 3.Основные 16‑ичные константы.. 5 4.Реализация целочисленных операций. 7 5.Представление отрицательных чисел. 8 6.Целочисленные типы данных в языке Си. 9 7.Вещественные типы данных в языке Си. 10 1. Позиционные системы счисленияПозиционные системы счисления (СС) – это системы счисления, в которых количественный эквивалент каждой цифры зависит от ее положения (позиции) в записи числа. Например: 1) шестидесятиричная (Древний Вавилон) – первая позиционная система счисления. До сих пор при измерении времени используется основание равное 60 (1 мин = 60 с, 1 ч = 60 мин); 2) двенадцатеричная система счисления (широкое распространение получила в XIX в. Число12 – «дюжина»: в сутках две дюжины часов. Счет не по пальцам. а по суставам пальцев. На каждом пальце руки, кроме большого, по 3 сустава – всего 12; 3) в настоящее время наиболее распространенными позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Система счисления – способ записи (изображения) чисел. Символы, при помощи которых записывается число, называются цифрами. Алфавитом системы счисления называется совокупность различных цифр, используемых в позиционной системе счисления для записи чисел. Например: Алфавиты некоторых позиционных систем счисления. Десятичная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} Двоичная система: {0, 1} Восьмеричная система: {0, 1, 2, 3, 4, 5, 6, 7} Шестнадцатеричная система: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F} Количество цифр в алфавите равно основанию системы счисления. Основанием позиционной системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления. Базисом позиционной системы счисления называется последовательность чисел, каждое из которых задает количественное значение или «вес» каждого разряда. Например: Базисы некоторых позиционных систем счисления. Десятичная система: 100 , 101 , 102 , 103 , 104 ,…, 10n ,… Двоичная система: 20 , 21 , 22 , 23 , 24 ,…, 2n ,… Восьмеричная система: 80 , 81 , 82 , 83 , 84 ,…, 8n ,… Свернутой формой записи числа называется запись в виде A=an -1 an -2 …a1 a0 .a-1 …a- m Именно такой формой записи чисел мы и пользуемся в повседневной жизни. Иначе свернутую форму записи называют естественной или цифровой. Пример . Десятичное число 4718,63, двоичное число 1001,1, восьмеричное число 7764,1, шестнадцатеричное число 3АF16 Позиция цифры в числе называется разрядом: разряд возрастает справа налево, от младших к старшим, начиная с нуля. В позиционной системе счисления любое вещественное число в развернутой форме может быть представлено в следующем десятичном виде: А= ± (an-1 qn-1 +an-2 qn-2 + … +a0 q0 +a-1 q-1 +a-2 q-2 + … +a- m q- m ) Здесь А – само число, q – основание системы счисления, ai – цифры, принадлежащие алфавиту данной системы счисления, n – число целых разрядов числа, m – число дробных разрядов числа. Развернутая форма записи числа – сумма произведений коэффициентов на степени основания системы счисления. Пример . Десятичное число А10 = 4718,63 в развернутой форме запишется так: А10 = 4·103 + 7·102 + 1·101 + 8·100 + 6·10-1 + 3·10-2 Двоичное число А2 = 1001,1 = 1·23 + 0·22 + 0·21 + 1·20 + 1·2-1 Восьмеричное число А8 = 7764,1 = 7·83 + 7·82 + 6·81 + 4·80 + 1·8-1 Шестнадцатеричное число А16 = 3АF16 = 3·162 + 10·161 + 15·160 2. Переходы между основными системами счисленияОсновные СС имеют основания 2, 8,10, 16. Системы с основаниями 2, 8 и 16 являются родственными, так как их основания являются степенями двойки. Переходы между ними реализуются легко. 2 ® 8. Двоичное число разбивается справа налево на триады (тройки цифр) и каждая триада заменяется на 8‑ичную цифру. 2 ® 16. Двоичное число разбивается справа налево на тетрады (четверки цифр) и каждая тетрада заменяется на 16‑ичную цифру. 8 ® 16 и 16 ® 8. Преобразование идет через двоичную СС. Любое основание ® 10. Осуществляется по определению позиционной системы счисления. 10 ® 16. Имеется два способа преобразования. 1. Метод деления «уголком» строит результирующее 16‑ичное число от младших цифр к старшим. Для этого запоминаются целые остатки от деления исходного числа на 16, пока частное не станет равным 0. Записывая эти остатки в обратном порядке, получим ответ. 2. Метод «вычерпывания» состоит из нескольких итераций. На каждой итерации исходное число х оценивается снизу максимальной степенью m нового основания p= 16: х ≥ 16m . Затем определяем число r вхождений степени 16m в число х. Наконец, 16‑ичную цифру r записываем в результирующее число в разряд с номером m. Число x заменяем на меньшее число х – r · 16m . Если новое число х = 0, то алгоритм заканчивается, и остальные разряды результата заполняем нулями. В противном случае, переходим к следующей итерации. 3. Основные 16‑ичные константыБольшинство числовых констант, которые встречаются в компьютерной технике, являются круглыми шестнадцатеричными числами. Эти числа обычно записывают в десятично-буквенном виде, имеющем формат ab, где а – десятичное число, b – буква. Таблица 1.Шестнадцатеричные константы
Следующая таблица содержит популярные степени числа 2, а также их русские и английские названия. Таблица 2. Степени числа 2
Последние строки кратных единиц были дополнены ГОСТом в 1991. Вычисления с числами, представленными в десятично-буквенном виде, можно осуществлять без перехода в десятичную СС. Например, 32 Т / 256 К = 245 / 218 = 227 = 128 М. Таблицы 1 и 2 позволяют переводить 16‑ичные числа в десятично-буквенную запись без применения вычислительных средств. Например, Отметим, что для десятично-буквенных чисел не выполняется дистрибутивный закон, то есть 1 М + 100 К не равен 1,1 М. 4. Реализация целочисленных операцийПредставление чисел в компьютере осуществляется в двоичной СС. Однако для краткости записи чисел используют родственную 16‑ичную СС. Определение 1 . Логическим адресом ячейки памяти в ОЗУ с 20‑битной адресной шиной называется запись xxxx:yyyy, где хххх – шестнадцатеричный сегментный адрес, yyyy – шестнадцатеричное смещение. Физическим адресом этой ячейки называется число xxxx0 + yyyy. Пример . Область кода программы расположена с ячейки 55А3:3000 по ячейку 9EEF:A0FF. Оценить размер области в килобайтах. Решение . Физический адрес начала области 0х55А30 + 0х3000 = 0х58A30, конца области 0х9EEF0 + 0хA0FF = 0хA8FEF. Размер этой области равен 0хA8FEF– 0х58A30 + 1 = 0x505C0 = 5·64 К + 0·4 К + 10· (К/4) + 12·16= (320 + 2,5) К + 192 = 322,5 К + 192. Определение 2 . Нормализованным адресом ячейки памяти ОЗУ с 20‑битной адресной шиной называется запись xxxx:yyyy, где хххх – шестнадцатеричное число, yyyy – шестнадцатеричное смещение, не превосходящее размера параграфа, то есть из диапазона от 0 до 15. Арифметические операции сложения, вычитания, умножения и деления с 16‑ичными числами осуществляются аналогично 10‑ичным числам, то есть «столбиком». Однако, имеются некоторые отличия. Пример . Критерии деления 16‑ичного целого числа на 3 и на 5 выглядят одинаково: сумма цифр должна делится, соответственно, на 3 и на 5. Пример . Оказывается в 16‑ичной СС 0x112 = 0x121, 0x122 = 0x144, 0x132 = 0x169. Пример
. Десятичное число 0,1 нельзя представить в виде конечной 2‑ичной дроби A= 0, a-1
…a-
m
= a-1
2-1
+ a-2
2-2
+… + a-
m
2-
m
. В противном случае, умножая равенство 0,1 = А на 10·2m
, получим 2m
= 10·(a-1
2m
-1
+ 5. Представление отрицательных чиселЦелые отрицательные числа хранятся в компьютере в двоичном «дополнительном» коде: положительное двоичное число необходимо побитово инвертировать и прибавить единицу. Этот код основан на простом соображении, что x+ (-x) = 0 при сложении двоичных чисел столбиком. При этом единица, которая переходит из старшего 7‑го бита в несуществующий 8‑ой бит, пропадает. Например, для однобайтного числа x = 5 имеем x = 5 = 0000 0101 + – x = -5 = **** **** ____________________ 0 = 0 = 0000 0000 Теперь конструируем число -5 = 1111 1011. 6. Целочисленные типы данных в языке СиТаблица 3. Целочисленные типы данных
По умолчанию целые десятичные константы имеют тип int. Поэтому все целые числа должны содержаться в диапазоне -32758… 32757. Например, запись x = 100000 будет ошибочна независимо от типа переменной x. Для обозначения целой константы типа long используется суффикс l. Тогда инициализация longx = 100000l будет корректна. Компилятор не проверяет выход результата целочисленного выражения за диапазон типа. Запись longx = 20000 + 20000 будет ошибочна, так как 40000 не содержится в диапазоне типа int. Это будет «хорошо скрытая» ошибка. Реально x будет содержать значение Построим область корректного сложения для типа char. char x, y, z; x = y = 100; z = x + y; Нарисуем в системе координат (x, y) множество, для которого z будет содержать корректный ответ. Имеем систему
решением которой является шестиугольник.
Рис. 1. Диапазон корректного сложения 7. Вещественные типы данных в языке СиВещественные типы всегда имеют знак. Определение 3 . Нормализованной формой ненулевого числа x называется запись x = M×10p , где M– мантисса, 0,1 £½M½ < 1, p – порядок числа х. Нормализованная форма числа единственна. Таблица 4. Вещественные типы данных
Определение 4 . Машинным нулем для данного вещественного типа называется минимальное положительное число того же типа m0 = min {x: x > 0}. Определение 5 . Машинным эпсилон для данного вещественного типа называется минимальное число того же типа, для которого 1 + x > 1 me = min {x: 1 + x > 1}. Определение 6 . Машинной бесконечностью для данного вещественного типа называется максимальное число того же типа m¥ = max{x}. По диапазону типа можно определить m0 , m¥ . Машинный эпсилон определяется размером мантиссы. Так, например, для типа float имеем m0 = 3,4×10-38 , m¥ = 3,4×1038 , me » 10-8 . Определение 7 . «Правым соседом» числа x данного вещественного типа назовем минимальное число y того же типа, для которого x < y «Правый сосед» х = min {y: x < y}. «Правый сосед» числа х больше самого х на величину равную me × 10порядок числа х . Приближенно можно считать, что «правый сосед» числа х » х + me ×x. Например, для типа float «правый сосед» числа 1010 » 1010 + 10-8 × 1010 = 1010 + 100. Таким образом, вещественные числа данного типа расположены на числовой прямой неравномерно, чем больше числа, тем больше расстояние между соседними числами. Этот факт следует учитывать при организации циклов: шаг цикла должен быть больше, чем расстояние между соседними числами. Параметры типа в таблице 4 связаны между собой. Задача . Вещественный тип doom занимает 15 байт, под порядок отведено 30 бит. Определить остальные параметры этого типа. Решение
. Порядок занимает 30 бит, поэтому минимальное двоичное значение порядка равно -229
. Для перевода этого числа к десятичному основанию решим показательное уравнение -229
= -10х
. Логарифмируя по основанию 10, получаем х = 29 ×lg2 » 29 × 0,3010 = 8,729. Таким образом, m0
равен Мантисса в двоичной системе счисления занимает 90 бит, из которых один бит определяет знак мантиссы. Так как первые знаки двоичной мантиссы равны 0,1 и всегда одинаковы, то под них память не отводится. Поэтому остальные 89 бит мантиссы занимают разряды с номерами от -2 до -90. «Правый сосед» единицы равен 0,100…0012 × 21 , где последняя единица стоит в -90‑ом разряде. Тогда me = 2-89 = 10-89 × lg (2) = 10-26 , 7 9 = 6,17 ×10-26 8. Кодирование символовДля кодирования символов с помощью одного байта используется ASCII‑таблица (AmericanStandardCodeforInformationInterchage) В ASCII‑таблице содержатся различные символы и соответствующие им коды. Например, символу ‘0’ соответствует код 0x30 = 48. Символы и строки хранятся в памяти в виде соответствующих кодов из ASCII‑таблицы. Например, строка «123» в памяти будет храниться в виде последовательности байт 0х31 0х32 0х33 0х00. Иногда строки, у которых 0 является признаком конца, называют asciiz‑строками. Таблица 5. ASCII – таблица символов
Символу ‘b’ соответствует «ASCII‑код» 0x62. В десятичной системе это будет 98, а в двоичной – 01100010. Код символа ‘b’ вы можете посмотреть из ASCII‑таблицы. Таблицы символов для разных шрифтов можно найти с помощью программы Таблица Символов: Пуск – Стандартные – Системные утилиты – Таблица Символов). В русской кодировочной странице 866 буква Ё имеет код 0xF0, а буква ё – код 0хF1. В языке Си символьные константы обозначаются ‘\xxx’, где ххх – код этого символа, записанный в восьмеричной СС. Иначе говоря, Примеры
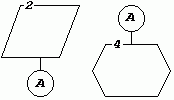
. 1. Количество букв в английском алфавите равно 2. Количество букв в русском алфавите равно ‘Я’ – ‘А’ + 2. 9. Схемы алгоритмовДля облегчения вычерчивания и нахождения на схеме символов рекомендуется поле листа разбивать на зоны. Размеры зон устанавливают с учетом минимальных размеров символов, изображенных на данном листе. Допускается один символ размещать в двух и более зонах, если размер символа превышает размер зоны. Координаты зоны проставляют: по горизонтали – арабскими цифрами слева направо в верхней части листа; по вертикали – прописными буквами латинского алфавита сверху вниз в левой части листа. Координаты зон в виде сочетания букв и цифр присваивают символам, вписанным в поля этих зон, например: A1, A2, A3, B1, B2, B3 и т.д. Если поле листа не разбито на зоны, символам присваивают порядковые номера. Линии потока должны быть параллельны линиям внешней рамки схемы. Направления линий потока сверху вниз и слева направо принимают за основные и, если линии потока не имеют изломов, стрелками можно не обозначать. В остальных случаях направление линии потока обозначать стрелкой обязательно. Сокращения слов и аббревиатуры, кроме стандартных и общепринятых, должны быть расшифрованы в нижней части поля схемы или в документе, к которому эта схема относится. Записи внутри символа должны быть представлены так, чтобы их можно было читать слева направо и сверху вниз, независимо от направления потока. (вид а должен быть прочитан как вид б ).
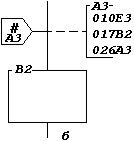
Рис. 2. Эквивалентные фрагменты схемы алгоритма Таблица 6. Соединитель
Таблица 7. Межстраничный соединитель
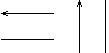
Таблица 8. Линии потока
Таблица 9. Возможные варианты отображения решения
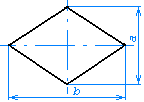
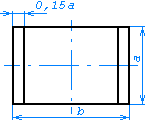
Таблица 10 Символы в схемах алгоритмов
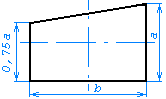
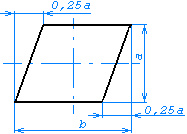
Размер a должен выбираться из ряда 10, 15, 20 мм. Допускается увеличивать размер a на число, кратное 5. Размер b равен 1,5 × a. При ручном выполнении схем алгоритмов и программ допускается устанавливать b равным 2 × a. |