| Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет
им. Ф. Скорины»
Математический факультет
Кафедра алгебры и геометрии
О сверхразрешимости некоторых классов
факторизуемых групп
Курсовая работа
Исполнитель:
Студентка группы М-31
____________ Леванюк А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
____________ Скиба М.Т.
Гомель 2005
Содержание
Перечень условных обозначений
Введение
1 Факторизуемые группы с 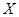 -перестановочными подгруппами -перестановочными подгруппами
2 Факторизуемые группы с 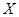 -перестановочными силовскими подгруппами
-перестановочными силовскими подгруппами
Заключение
Литература
Перечень условных обозначений
В работе все рассматриваемые группы предполагаются конечными. Используются обозначения, принятые в книгах. Буквами  обозначаются простые числа. обозначаются простые числа.
Будем различать знак включения множеств  и знак строгого включения и знак строгого включения 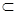 ; ;
 и и 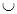 --- соответственно знаки пересечения и объединения множеств; --- соответственно знаки пересечения и объединения множеств;
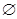 --- пустое множество; --- пустое множество;
 --- множество всех --- множество всех  для которых выполняется условие для которых выполняется условие  ; ;
 --- множество всех натуральных чисел; --- множество всех натуральных чисел;
 --- множество всех простых чисел; --- множество всех простых чисел;
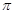 --- некоторое множество простых чисел, т.е. --- некоторое множество простых чисел, т.е. 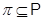 ; ;
 --- дополнение к --- дополнение к 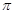 во множестве всех простых чисел; в частности, во множестве всех простых чисел; в частности,  ; ;
примарное число --- любое число вида 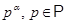 ; ;
Пусть  --- группа. Тогда: --- группа. Тогда:
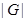 --- порядок группы --- порядок группы  ; ;
 --- порядок элемента --- порядок элемента  группы группы  ; ;
 --- единичный элемент и единичная подгруппа группы --- единичный элемент и единичная подгруппа группы  ; ;
 --- множество всех простых делителей порядка группы --- множество всех простых делителей порядка группы  ; ;
 --- множество всех различных простых делителей натурального числа --- множество всех различных простых делителей натурального числа 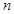 ; ;
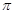 --группа --- группа --группа --- группа  , для которой , для которой  ; ;
 --группа --- группа --группа --- группа  , для которой , для которой  ; ;
 --- подгруппа Фраттини группы --- подгруппа Фраттини группы  , т.е. пересечение всех максимальных подгрупп группы , т.е. пересечение всех максимальных подгрупп группы  ; ;
 --- подгруппа Фиттинга группы --- подгруппа Фиттинга группы  , т.е. произведение всех нормальных нильпотентных подгрупп группы , т.е. произведение всех нормальных нильпотентных подгрупп группы  ; ;
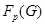 --- наибольшая нормальная --- наибольшая нормальная  -нильпотентная подгруппа группы -нильпотентная подгруппа группы  ; ;
 --- коммутант группы --- коммутант группы  , т.е. подгруппа, порожденная коммутаторами всех элементов группы , т.е. подгруппа, порожденная коммутаторами всех элементов группы  ; ;
 --- --- 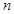 -ый коммутант группы -ый коммутант группы  ; ;
 --- наибольшая нормальная --- наибольшая нормальная  -подгруппа группы -подгруппа группы  ; ;
 --- --- 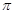 --холловская подгруппа группы --холловская подгруппа группы  ; ;
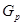 --- силовская --- силовская  --подгруппа группы --подгруппа группы  ; ;
 --- дополнение к силовской --- дополнение к силовской  --подгруппе в группе --подгруппе в группе  , т.е. , т.е.  --холловская подгруппа группы --холловская подгруппа группы  ; ;
 --- группа всех автоморфизмов группы --- группа всех автоморфизмов группы  ; ;
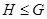 --- ---  является подгруппой группы является подгруппой группы  ; ;
 --- ---  является собственной подгруппой группы является собственной подгруппой группы  ; ;
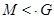 --- ---  является максимальной подгруппой группы является максимальной подгруппой группы  ; ;
нетривиальная подгруппа --- неединичная собственная подгруппа;
 --- ---  является нормальной подгруппой группы является нормальной подгруппой группы  ; ;
 --- подгруппа --- подгруппа  характеристична в группе характеристична в группе  , т.е. , т.е. 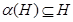 для любого автоморфизма для любого автоморфизма  ; ;
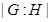 --- индекс подгруппы --- индекс подгруппы  в группе в группе  ; ;
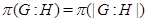 ; ;
 --- централизатор подгруппы --- централизатор подгруппы  в группе в группе  ; ;
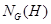 --- нормализатор подгруппы --- нормализатор подгруппы  в группе в группе  ; ;
 --- центр группы --- центр группы  ; ;
 --- циклическая группа порядка --- циклическая группа порядка 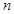 ; ;
 --- ядро подгруппы --- ядро подгруппы  в группе в группе  , т.е. пересечение всех подгрупп, сопряжённых с , т.е. пересечение всех подгрупп, сопряжённых с  в в  . .
Если 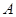 и и  --- подгруппы группы --- подгруппы группы  , то: , то:
 --- прямое произведение подгрупп --- прямое произведение подгрупп 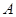 и и  ; ;
 --- полупрямое произведение нормальной подгруппы --- полупрямое произведение нормальной подгруппы 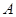 и подгруппы и подгруппы  ; ;
 --- --- 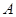 и и  изоморфны. изоморфны.
Группа  называется: называется:
примарной, если  ; ;
бипримарной, если  . .
Скобки 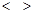 применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп. применяются для обозначения подгрупп, порождённых некоторым множеством элементов или подгрупп.
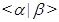 --- подгруппа, порожденная всеми --- подгруппа, порожденная всеми  , для которых выполняется , для которых выполняется 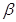 . .
 , где , где 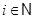 . .
Группу  называют: называют:
 -замкнутой, если силовская -замкнутой, если силовская  -подгруппа группы -подгруппа группы  нормальна в нормальна в 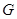 ; ;
 -нильпотентной, если -нильпотентной, если  -холловская подгруппа группы -холловская подгруппа группы 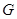 нормальна в нормальна в 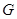 ; ;
 -разрешимой, если существует нормальный ряд, факторы которого либо -разрешимой, если существует нормальный ряд, факторы которого либо  -группы, либо -группы, либо  -группы; -группы;
 -сверхразрешимой, если каждый ее главный фактор является либо -сверхразрешимой, если каждый ее главный фактор является либо  -группой, либо циклической группой; -группой, либо циклической группой;
нильпотентной, если все ее силовские подгруппы нормальны;
метанильпотентной, если существует нормальная нильпотентная подгруппа 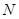 группы группы  такая, что такая, что  нильпотентна. нильпотентна.
разрешимой, если существует номер 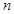 такой, что такой, что  ; ;
сверхразрешимой, если она обладает главным рядом, все индексы которого являются простыми числами.
Группа Шмидта --- это конечная ненильпотентная группа, все собственные группы которой нильпотентны.
Добавлением к подгруппе  группы группы 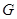 называется такая подгруппа называется такая подгруппа  из из 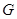 , что , что  . .
Минимальная нормальная подгруппа группы  --- неединичная нормальная подгруппа группы --- неединичная нормальная подгруппа группы 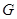 , не содержащая собственных неединичных нормальных подгрупп группы , не содержащая собственных неединичных нормальных подгрупп группы 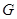 . .
Цоколь группы 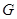 --- произведение всех минимальных нормальных подгрупп группы --- произведение всех минимальных нормальных подгрупп группы 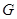 . .
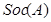 --- цоколь группы --- цоколь группы 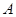 . .
Экспонента группы 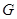 --- это наименьшее общее кратное порядков всех ее элементов. --- это наименьшее общее кратное порядков всех ее элементов.
Цепь --- это совокупность вложенных друг в друга подгрупп. Ряд подгрупп --- это цепь, состоящая из конечного числа членов и проходящая через единицу.
Ряд подгрупп  называется: называется:
субнормальным, если  для любого для любого  ; ;
нормальным, если  для любого для любого  ; ;
главным, если  является минимальной нормальной подгруппой в является минимальной нормальной подгруппой в  для всех для всех  . .
Классы групп, т.е. совокупности групп, замкнутые относительно изоморфизмов, обозначаются прописными готическими буквами. Также обозначаются формации, т.е. классы групп, замкнутые относительно факторгрупп и подпрямых произведений. За некоторыми классами закреплены стандартные обозначения:
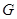 --- класс всех групп; --- класс всех групп;
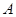 --- класс всех абелевых групп; --- класс всех абелевых групп;
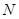 --- класс всех нильпотентных групп; --- класс всех нильпотентных групп;
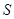 --- класс всех разрешимых групп; --- класс всех разрешимых групп;
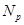 --- класс всех --- класс всех  --групп; --групп;
 --- класс всех сверхразрешимых групп; --- класс всех сверхразрешимых групп;
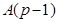 --- класс всех абелевых групп экспоненты, делящей --- класс всех абелевых групп экспоненты, делящей 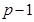 . .
Формации --- это классы конечных групп, замкнутые относительно взятия гомоморфных образов и конечных подпрямых произведений.
Пусть 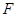 --- некоторый класс групп и --- некоторый класс групп и 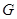 --- группа, тогда: --- группа, тогда:
 --- --- 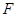 --корадикал группы --корадикал группы 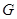 , т.е. пересечение всех тех нормальных подгрупп , т.е. пересечение всех тех нормальных подгрупп 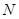 из из 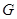 , для которых , для которых 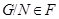 . Если . Если 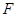 --- формация, то --- формация, то 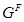 является наименьшей нормальной подгруппой группы является наименьшей нормальной подгруппой группы 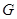 , факторгруппа по которой принадлежит , факторгруппа по которой принадлежит  . Если . Если 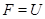 --- формация всех сверхразрешимых групп, то --- формация всех сверхразрешимых групп, то 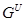 называется сверхразрешимым корадикалом группы называется сверхразрешимым корадикалом группы 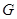 . .
Формация 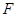 называется насыщенной, если всегда из называется насыщенной, если всегда из  следует, что и следует, что и 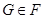 . .
Класс групп 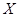 называется наследственным или замкнутым относительно подгрупп, если из того, что называется наследственным или замкнутым относительно подгрупп, если из того, что  следует, что и каждая подгруппа группы следует, что и каждая подгруппа группы 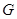 также принадлежит также принадлежит 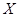 . .
Произведение формаций 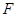 и и  состоит из всех групп состоит из всех групп 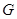 , для которых , для которых  . .
Введение
Понятие  -перестановочной подгруппы оказалось полезным инструментом в вопросах классификации непростых конечных групп. Отметим, в частности, что классическая теорема Холла о разрешимых группах на языке -перестановочной подгруппы оказалось полезным инструментом в вопросах классификации непростых конечных групп. Отметим, в частности, что классическая теорема Холла о разрешимых группах на языке  -перестановочных подгрупп может быть сформулирована так: Группа -перестановочных подгрупп может быть сформулирована так: Группа  разрешима тогда и только тогда, когда любые ее две силовские подгруппы разрешима тогда и только тогда, когда любые ее две силовские подгруппы  -перестановочны.
Согласно теореме 3.8 из группа -перестановочны.
Согласно теореме 3.8 из группа  является сверхразрешимой тогда и только тогда, когда все ее максимальные подгруппы является сверхразрешимой тогда и только тогда, когда все ее максимальные подгруппы  -перестановочны со всеми другими подгруппами этой группы. Новые характеризации в терминах -перестановочны со всеми другими подгруппами этой группы. Новые характеризации в терминах  -перестановочных подгрупп для класов разрешимых, сверхразрешимых и нильпотентных групп можно найти в работах . Целью данной главы является нахождение новых признаков сверхразрешимости группы на основе условий -перестановочных подгрупп для класов разрешимых, сверхразрешимых и нильпотентных групп можно найти в работах . Целью данной главы является нахождение новых признаков сверхразрешимости группы на основе условий  -перестановочности некоторых ее подгрупп. -перестановочности некоторых ее подгрупп.
1. Факторизуемые группы с  -перестановочными подгруппами -перестановочными подгруппами
В данном разделе, развивая основные наблюдения работы, мы дадим новые критерии сверхразрешимости групп.
Пусть  --- группа и --- группа и  --- ее подгруппа Фиттинга. Тогда --- ее подгруппа Фиттинга. Тогда  является сверхразрешимой в том и только том случае, когда является сверхразрешимой в том и только том случае, когда  , где , где  и и  --- такие сверхразрешимые подгруппы группы --- такие сверхразрешимые подгруппы группы  , что каждая подгруппа группы , что каждая подгруппа группы   -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 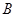 . .
Доказательство. Необходимость. Пусть  --- сверхразрешимая группа. Пусть --- сверхразрешимая группа. Пусть  --- минимальная нормальная подгруппа группы --- минимальная нормальная подгруппа группы  . Тогда . Тогда  для некоторого простого числа для некоторого простого числа  . Пусть . Пусть  --- такая максимальная подгруппа группы --- такая максимальная подгруппа группы  , что , что  . Тогда . Тогда 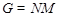 , ,  и и  сверхразрешимы и каждая подгруппа группы сверхразрешимы и каждая подгруппа группы  перестановочна с каждой подгруппой группы перестановочна с каждой подгруппой группы  . .
Достаточность. Предположим, что  --- произведение сверхразрешимых подгрупп --- произведение сверхразрешимых подгрупп 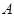 и и 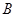 , , 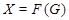 --- подгруппа Фиттинга группы --- подгруппа Фиттинга группы  и каждая подгруппа группы и каждая подгруппа группы 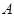  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 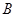 , но , но  не является сверхразрешимой группой. Допустим, что не является сверхразрешимой группой. Допустим, что  --- контрпример минимального порядка. Доказательство разобьем на следующие этапы. --- контрпример минимального порядка. Доказательство разобьем на следующие этапы.
(1) Если  --- максимальная подгруппа группы --- максимальная подгруппа группы  такая, что такая, что  и либо и либо  , либо , либо  , то , то  сверхразрешима. сверхразрешима.
Предположим, что  . Тогда по тождеству Дедекинда имеем . Тогда по тождеству Дедекинда имеем
 . .
Так как

то каждая подгруппа группы 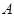  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 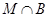 . Поскольку . Поскольку  , то по выбору группы , то по выбору группы  мы заключаем, что мы заключаем, что 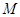 сверхразрешима. сверхразрешима.
(2) Для любой неединичной нормальной в  подгруппы подгруппы  факторгруппа факторгруппа 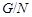 сверхразрешима. сверхразрешима.
Ясно, что  . Пусть . Пусть 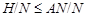 и и  . Так как по условию для некоторого . Так как по условию для некоторого  , ,

то мы имеем
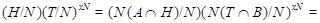

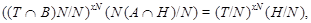
где 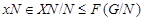 . Это показывает, что каждая подгруппа группы . Это показывает, что каждая подгруппа группы   -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  . Но поскольку . Но поскольку 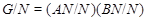 --- произведение сверхразрешимых подгрупп --- произведение сверхразрешимых подгрупп  и и 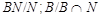 , то по выбору группы , то по выбору группы  мы заключаем, что мы заключаем, что 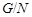 сверхразрешима. сверхразрешима.
(3) Группа  имеет абелеву минимальную нормальную погруппу. имеет абелеву минимальную нормальную погруппу.
Допустим, что  . Тогда ввиду (2), . Тогда ввиду (2),  --- сверхразрешимая группа и поэтому --- сверхразрешимая группа и поэтому  разрешима. Следовательно, разрешима. Следовательно,  имеет абелеву минимальную нормальную погруппу. имеет абелеву минимальную нормальную погруппу.
Предположим теперь, что  . Пусть . Пусть 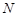 --- минимальная нормальная подгруппа группы --- минимальная нормальная подгруппа группы 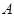 . Тогда по условию . Тогда по условию  . Предположим, что . Предположим, что  . Ввиду леммы мы видим, что . Ввиду леммы мы видим, что  . Но . Но 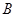 сверхразрешима, и поэтому минимальная нормальная подгруппа группы сверхразрешима, и поэтому минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в  , абелева. Пусть теперь , абелева. Пусть теперь  . Предположим, что . Предположим, что 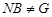 и пусть и пусть 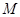 --- такая максимальная подгруппа группы --- такая максимальная подгруппа группы  , что , что  . Согласно (1), . Согласно (1), 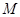 сверхразрешима, но сверхразрешима, но  , и поэтому ввиду леммы , , и поэтому ввиду леммы , 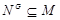 . Это показывает, что минимальная нормальная подгруппа группы . Это показывает, что минимальная нормальная подгруппа группы  , которая содержится в , которая содержится в  , абелева. Пусть теперь , абелева. Пусть теперь  . Так как . Так как  , то каждая подгруппа группы , то каждая подгруппа группы  перестановочна с каждой погруппой группы перестановочна с каждой погруппой группы  . Пусть . Пусть  --- минимальная нормальная подгруппа группы --- минимальная нормальная подгруппа группы  . Тогда . Тогда 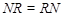 . Предположим, что . Предположим, что  . Ввиду леммы мы видим, что . Ввиду леммы мы видим, что 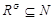 . Но . Но  сверхразрешима, и поэтому минимальная нормальная подгруппа группы сверхразрешима, и поэтому минимальная нормальная подгруппа группы  , содержащаяся в , содержащаяся в  , абелева. Пусть теперь , абелева. Пусть теперь  . Предположим, что . Предположим, что  и пусть и пусть  --- такая максимальная подгруппа группы --- такая максимальная подгруппа группы  , что , что 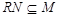 . Согласно (1), . Согласно (1),  сверхразрешима, но сверхразрешима, но  , и поэтому ввиду леммы , , и поэтому ввиду леммы , 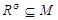 . Это показывает, что минимальная нормальная подгруппа группы . Это показывает, что минимальная нормальная подгруппа группы  , которая содержится в , которая содержится в  , абелева. Следовательно, , абелева. Следовательно,  . Поскольку . Поскольку  и и  абелевы группы, то группа абелевы группы, то группа  имеет абелеву минимальную нормальную подгруппу. имеет абелеву минимальную нормальную подгруппу.
(4) Группа  имеет единственную минимальную нормальную подгруппу имеет единственную минимальную нормальную подгруппу  и и  , где , где 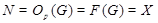 и и  --- такая максимальная в --- такая максимальная в  подгруппа, что подгруппа, что
 и и  . .
Пусть  --- произвольная минимальная нормальная подгруппа группы --- произвольная минимальная нормальная подгруппа группы  . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то  --- единственная минимальная нормальная подгруппа в --- единственная минимальная нормальная подгруппа в  , причем , причем  . Пусть . Пусть 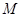 --- максимальная подгруппа в --- максимальная подгруппа в  такая, что такая, что  и пусть и пусть  . Тогда по тождеству Дедекинда мы имеем . Тогда по тождеству Дедекинда мы имеем  . Так как ввиду (3), . Так как ввиду (3),  абелева, то абелева, то  и и  . Это показывает, что . Это показывает, что 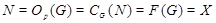 . Следовательно, . Следовательно,  --- сверхразрешимая группа и ввиду леммы --- сверхразрешимая группа и ввиду леммы  . Согласно (2) и выбора группы . Согласно (2) и выбора группы  , мы имеем , мы имеем 
(5)  --- наибольший простой делитель порядка группы --- наибольший простой делитель порядка группы  . .
Предположим, что  не является наибольшим простым делителем порядка группы не является наибольшим простым делителем порядка группы  , и пусть , и пусть  --- наибольший простой делитель --- наибольший простой делитель 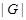 . Пусть . Пусть 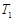 и и  --- такие максимальные подгруппы группы --- такие максимальные подгруппы группы  , что , что  , ,  . Тогда . Тогда  . По лемме, . По лемме, 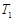 и и  не сопряжены в не сопряжены в  . Так как ввиду леммы все максимальные подгруппы группы . Так как ввиду леммы все максимальные подгруппы группы  , которые не содержат , которые не содержат  , сопряжены в , сопряжены в  , то либо , то либо  содержит содержит  , либо , либо  содержит содержит  . Пусть, например, . Пусть, например, 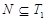 и пусть и пусть 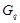 --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Предположим, что . Предположим, что  . Согласно (2), . Согласно (2), 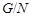 сверхразрешима и поскольку сверхразрешима и поскольку 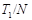 максимальная подгруппа группы максимальная подгруппа группы 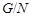 , то по лемме , то по лемме  --- простое число. Значит, --- простое число. Значит,  содержит неединичную силовскую содержит неединичную силовскую  -подгруппу -подгруппу  . Согласно лемме , . Согласно лемме ,  , и поэтому , и поэтому  . Это противоречие показывает, что . Это противоречие показывает, что  . Ясно, что . Ясно, что  . Тогда . Тогда  . Предположим, что . Предположим, что  и пусть и пусть  --- максимальная подгруппа группы --- максимальная подгруппа группы  , содержащая , содержащая  . Ввиду (1), . Ввиду (1),  сверхразрешима. Без ограничения общности, мы можем предположить, что сверхразрешима. Без ограничения общности, мы можем предположить, что  . Так как группа . Так как группа  сверхразрешима, то сверхразрешима, то  , и поэтому , и поэтому 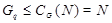 , что невозможно в силу (4). Значит, , что невозможно в силу (4). Значит, 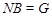 . Следовательно, по тождеству Дедекинда мы имеем . Следовательно, по тождеству Дедекинда мы имеем
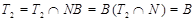
и поэтому 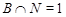 . Пусть . Пусть  , где , где  . Предположим, что . Предположим, что  . Тогда . Тогда  , и очевидно , и очевидно 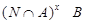 . Это влечет . Это влечет  . Следовательно, . Следовательно, 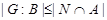 . Ясно, что . Ясно, что  , и поэтому , и поэтому  . Пусть . Пусть  --- максимальная подгруппа группы --- максимальная подгруппа группы  . Тогда для некоторого . Тогда для некоторого  , мы имеем , мы имеем  . Так как . Так как  не является сверхразрешимой группой, то ввиду (4) мы видим, что не является сверхразрешимой группой, то ввиду (4) мы видим, что  . Но поскольку . Но поскольку  , то приходим к противоречию. Следовательно, , то приходим к противоречию. Следовательно,  . Пусть . Пусть 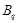 --- силовская --- силовская  -подгруппа группы -подгруппа группы  и для некоторого и для некоторого  , ,  . Предположим, что . Предположим, что  . Пусть . Пусть  --- максимальная подгруппа группы --- максимальная подгруппа группы  , содержащая , содержащая  . Согласно (1), . Согласно (1),  сверхразрешима. Это влечет сверхразрешима. Это влечет 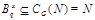 , противоречие. Следовательно, , противоречие. Следовательно,  . Предположим теперь, что . Предположим теперь, что 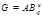 . В этом случае . В этом случае  , и поэтому каждая силовская , и поэтому каждая силовская  -подгруппа группы -подгруппа группы  является силовской является силовской  -подгруппой группы -подгруппой группы  . Следовательно, . Следовательно,  . Это противоречие показывает, что . Это противоречие показывает, что  , и поэтому , и поэтому 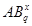 --- максимальная подгруппа группы --- максимальная подгруппа группы  . Согласно лемме , мы имеем . Согласно лемме , мы имеем 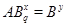 , для некоторого , для некоторого 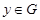 . Это противоречие показывает, что . Это противоречие показывает, что  --- наибольший простой делитель порядка группы --- наибольший простой делитель порядка группы  . .
(6)  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . .
Предположим, что это не верно. Тогда 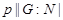 . Отсюда следует, что . Отсюда следует, что  , и поэтому ввиду (5) и леммы , , и поэтому ввиду (5) и леммы ,  , что невозможно в силу (4). Значит, , что невозможно в силу (4). Значит,  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . .
(7) Заключительное противоречие.
Без ограничения общности мы можем предположить, что  . Так как . Так как  сверхразрешима, то ввиду (5), сверхразрешима, то ввиду (5),  имеет нормальную подгруппу имеет нормальную подгруппу  порядка порядка  . Согласно (6), . Согласно (6),  Пусть Пусть  --- холлова --- холлова  -подгруппа группы -подгруппа группы  и для некоторого и для некоторого  , , 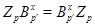 . Поскольку . Поскольку

то  . Согласно (6), силовская . Согласно (6), силовская  -подгруппа группы -подгруппа группы  содержится в содержится в  Тогда Тогда  и поэтому и поэтому  что невозможно в силу (4). Это противоречие завершает доказательство теоремы. что невозможно в силу (4). Это противоречие завершает доказательство теоремы.
Пусть  --- группа и --- группа и  --- ее подгруппа Фиттинга. Тогда --- ее подгруппа Фиттинга. Тогда  является сверхразрешимой в том и только том случае, когда является сверхразрешимой в том и только том случае, когда  , где , где  и и  --- нильпотентные подгруппы группы --- нильпотентные подгруппы группы  и и  имеет такой главный ряд имеет такой главный ряд

что каждая   -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  , для всех , для всех 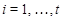 . .
Доказательство. Необходимость. Предположим, что  --- сверхразрешимая группа. Тогда согласно лемме , --- сверхразрешимая группа. Тогда согласно лемме , 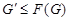 . Пусть . Пусть  и и  --- такая подгруппа группы --- такая подгруппа группы  , что , что  и и 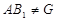 для каждой собственной подгруппы для каждой собственной подгруппы  группы группы  . Тогда . Тогда 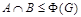 . Так как подгруппы . Так как подгруппы 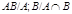 и и  нильпотентны, то нильпотентны, то  --- нильпотентная подгруппа. Рассмотрим главный ряд группы --- нильпотентная подгруппа. Рассмотрим главный ряд группы  , проходящий через , проходящий через 
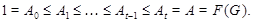
Поскольку  --- простое число для каждого --- простое число для каждого  , то этот ряд является главным рядом группы , то этот ряд является главным рядом группы  и каждая подгруппа и каждая подгруппа 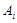 перестановочна со всеми подгруппами группы перестановочна со всеми подгруппами группы  для каждого для каждого 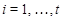 . .
Достаточность. Предположим теперь, что  , где , где  --- нильпотентные подгруппы группы --- нильпотентные подгруппы группы  и группа и группа  имеет такой главный ряд имеет такой главный ряд

что каждый член этого ряда  -перестановочен с каждой подгруппой группы -перестановочен с каждой подгруппой группы  . Покажем, что . Покажем, что  сверхразрешима. Предположим, что сверхразрешима. Предположим, что  не является сверхразрешимой группой, и пусть не является сверхразрешимой группой, и пусть  --- контрпример минимального порядка. Без ограничения общности мы может предположить, что --- контрпример минимального порядка. Без ограничения общности мы может предположить, что  и и 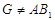 для каждой собственной подгруппы для каждой собственной подгруппы 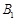 группы группы  . Для начала заметим, что поскольку группа . Для начала заметим, что поскольку группа  является произведением двух нильпотентных подгрупп, то по известной теореме Кегеля , группа является произведением двух нильпотентных подгрупп, то по известной теореме Кегеля , группа  разрешима. Доказательство разобьем на следующие этапы. разрешима. Доказательство разобьем на следующие этапы.
(1) Для любой неединичной нормальной в  подгруппы подгруппы  факторгруппа факторгруппа 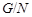 сверхразрешима. сверхразрешима.
Ясно, что  где где 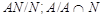 и и 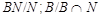 нильпотентны. Рассмотрим в нильпотентны. Рассмотрим в  ряд ряд

Без ограничения общности, мы можем предположить, что все члены этого ряда различны.
Пусть 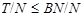 . Так как по условию для некоторого . Так как по условию для некоторого  , ,

то мы имеем



где 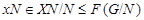 и и 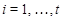 . Это показывает, что каждый член ряда (2) . Это показывает, что каждый член ряда (2)  -перестановочен со всеми подгруппами группы -перестановочен со всеми подгруппами группы  . .
Поскольку  то то  Так как Так как  --- простое число, то --- простое число, то  также является простым числом. Следовательно, ряд (2) является главным рядом группы также является простым числом. Следовательно, ряд (2) является главным рядом группы  . Поскольку . Поскольку 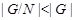 , то по выбору группы , то по выбору группы  мы заключаем, что мы заключаем, что 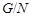 сверхразрешима. сверхразрешима.
(2) Группа  имеет единственную минимальную нормальную подгруппу имеет единственную минимальную нормальную подгруппу  и и  , где , где  и и 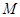 --- такая максимальная в --- такая максимальная в  подгруппа, что подгруппа, что  и и  . .
Пусть  --- произвольная минимальная нормальная подгруппа группы --- произвольная минимальная нормальная подгруппа группы  . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то  --- единственная минимальная нормальная подгруппа в --- единственная минимальная нормальная подгруппа в  , причем , причем 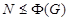 . Пусть . Пусть  --- максимальная подгруппа в --- максимальная подгруппа в  такая, что такая, что  и пусть и пусть  . Тогда по тождеству Дедекинда мы имеем . Тогда по тождеству Дедекинда мы имеем  . Так как . Так как  разрешима, то разрешима, то  --- элементарная абелева --- элементарная абелева  -группа для некоторого простого -группа для некоторого простого  и поэтому и поэтому  и и  . Это показывает, что . Это показывает, что 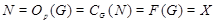 . Следовательно, . Следовательно,  --- сверхразрешимая группа и ввиду леммы --- сверхразрешимая группа и ввиду леммы  . Согласно (1) и выбора группы . Согласно (1) и выбора группы  , мы имеем , мы имеем  . .
(3)  и и  имеют не простые порядки. имеют не простые порядки.
Действительно, если для некоторого простого  , ,  , то в группе , то в группе  каждая подгруппа группы каждая подгруппа группы   -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  и поэтому по теореме, и поэтому по теореме,  сверхразрешима, что противоречит выбору группы сверхразрешима, что противоречит выбору группы  . Следовательно, . Следовательно, 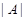 не является простым числом. Предположим теперь, что не является простым числом. Предположим теперь, что 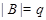 . Допустим, что . Допустим, что  . Тогда . Тогда  . Так как . Так как  нильпотентна, то ввиду(2), нильпотентна, то ввиду(2),  --- ---  -группа. Покажем теперь, что -группа. Покажем теперь, что  . Предположим, что . Предположим, что  . Так как . Так как 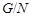 сверхразрешима, то сверхразрешима, то 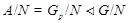 . Но поскольку . Но поскольку 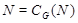 , то согласно лемме, , то согласно лемме,  , и поэтому , и поэтому  . Предположим теперь, что . Предположим теперь, что 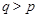 . В этом случае, для некоторого . В этом случае, для некоторого  , ,

Так как,
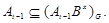
Значит,  . Покажем, что условия теоремы справедливы для подгруппы . Покажем, что условия теоремы справедливы для подгруппы  . Ясно, что . Ясно, что  , где , где  и и  --- нильпотентные подгруппы и подгруппа --- нильпотентные подгруппы и подгруппа  имеет главный ряд имеет главный ряд

где  . Пусть . Пусть  . Тогда . Тогда  . По условию, для некоторого . По условию, для некоторого 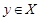 , мы имеем , мы имеем  . Поскольку . Поскольку  и и  , то , то  . Это означает, что каждая подгруппа . Это означает, что каждая подгруппа 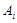 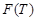 -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 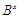 , для всех , для всех  . Поскольку . Поскольку  , то по выбору группы , то по выбору группы  мы заключаем, что мы заключаем, что  сверхразрешима. Значит, сверхразрешима. Значит,  . Отсюда следует, что . Отсюда следует, что  , противоречие. Таким образом, , противоречие. Таким образом,  . Следовательно, . Следовательно,  --- силовская --- силовская  -подгруппа группы -подгруппа группы  и поэтому и поэтому  --- максимальная подгруппа группы --- максимальная подгруппа группы  . Поскольку для некоторого . Поскольку для некоторого  , ,  и и  максимальная подгруппа группы максимальная подгруппа группы  , ,  , то , то  . Получили противоречие с нашим предположением о группе . Получили противоречие с нашим предположением о группе  . Значит, . Значит,  . По условию, . По условию, 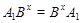 , для некоторого , для некоторого 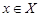 и поэтому и поэтому  . Согласно лемме , . Согласно лемме ,  . Так как порядок группы . Так как порядок группы  является не простым числом, то является не простым числом, то  . Отсюда следует, что . Отсюда следует, что 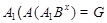 , что невозможно в силу (2). Этим доказано (3). , что невозможно в силу (2). Этим доказано (3).
(4)  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . .
Допустим, что наше предположение не верно. Пусть  --- наибольший простой делитель порядка группы --- наибольший простой делитель порядка группы  . Так как . Так как  и согласно (2), и согласно (2),  . Пусть . Пусть  --- максимальная подгруппа группы --- максимальная подгруппа группы  . По условию для некоторых, . По условию для некоторых,  , ,  и и  . Согласно (3), . Согласно (3),  и и 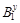 неединичные группы. Так как группы неединичные группы. Так как группы 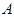 и и  нильпотентны, то нильпотентны, то  и и  . Ввиду леммы , . Ввиду леммы ,  и и 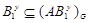 . Отсюда следует, что . Отсюда следует, что 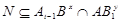 . Ясно,что либо . Ясно,что либо  , либо , либо  . Допустим, что . Допустим, что  . Покажем, что . Покажем, что 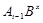 --- сверхразрешимая группа. Подгруппы --- сверхразрешимая группа. Подгруппы  и и 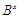 нильпотентны и подгруппа нильпотентны и подгруппа  имеет главный ряд имеет главный ряд
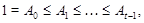
где 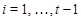 . Пусть . Пусть  . Тогда . Тогда  . По условию, для некоторого . По условию, для некоторого 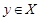 , мы имеем , мы имеем

Поскольку  и и  , то , то  . Это означает, что каждая подгруппа . Это означает, что каждая подгруппа 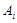  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 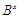 , для всех , для всех 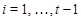 . Поскольку . Поскольку 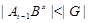 , то по выбору группы , то по выбору группы 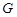 мы заключаем, что мы заключаем, что  сверхразрешима. Пусть сверхразрешима. Пусть 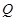 --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Тогда ввиду леммы , . Тогда ввиду леммы ,  , и поэтому , и поэтому 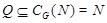 , противоречие. Пусть теперь, , противоречие. Пусть теперь,  . Покажем, что группа . Покажем, что группа  сверхразрешима. Ясно, что сверхразрешима. Ясно, что  и и 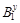 --- нильпотентные подгруппы и подгруппа --- нильпотентные подгруппы и подгруппа  имеет главный ряд имеет главный ряд

где  . Пусть . Пусть 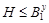 . Тогда . Тогда  . По условию, для некоторого . По условию, для некоторого  , мы имеем , мы имеем

Поскольку 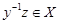 и и  , то , то  . Это означает, что каждая . Это означает, что каждая 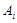  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  , для всех , для всех  . Поскольку . Поскольку  , то по выбору группы , то по выбору группы  мы заключаем, что мы заключаем, что 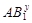 сверхразрешима. Пусть сверхразрешима. Пусть  --- силовская --- силовская  -подгруппа группы -подгруппа группы 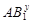 . Тогда ввиду леммы , . Тогда ввиду леммы , 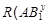 , и поэтому , и поэтому 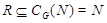 , противоречие. Следовательно, (4) справедливо. , противоречие. Следовательно, (4) справедливо.
(5) 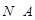 и и  . .
Предположим, что 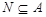 . Поскольку . Поскольку  нильпотента, то нильпотента, то   -группа, и поэтому согласно (4), -группа, и поэтому согласно (4),  --- силовская --- силовская  -подгруппа группы -подгруппа группы 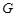 . Ясно, что . Ясно, что 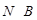 и и  . Тогда . Тогда  . Пусть . Пусть  --- такой элемент из --- такой элемент из  , что , что  . Тогда . Тогда  . Так как . Так как 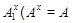 , то , то 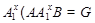 и поэтому и поэтому  , противоречие. Значит, , противоречие. Значит,  . .
Пусть теперь,  . Так как . Так как  --- нильпотентная группа, то ввиду (4), --- нильпотентная группа, то ввиду (4),  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Поскольку . Поскольку 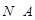 и и 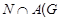 , то , то 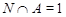 . Пусть . Пусть  --- максимальная подгруппа группы --- максимальная подгруппа группы  и и 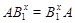 , где , где  . Согласно (3), . Согласно (3),  и и  . Поскольку . Поскольку  , то , то

и поэтому 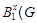 . Следовательно, . Следовательно,  , противоречие. Значит, , противоречие. Значит,  . .
(6) Заключительное противоречие.
Пусть  --- холлова --- холлова 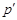 -подгруппа группы -подгруппа группы  . Допустим, что . Допустим, что  . Тогда . Тогда 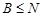 . Поскольку по условию, . Поскольку по условию,  , для некоторого , для некоторого 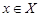 , и , и 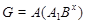 , то согласно лемме , , то согласно лемме ,  . Так как . Так как  и и  , то , то  . Значит, . Значит, 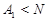 и и  , противоречие с (2). Следовательно, , противоречие с (2). Следовательно, 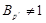 . По условию, . По условию,
 , ,
где 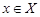 . Поскольку . Поскольку  , то , то
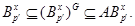
Тогда  , и поэтому , и поэтому  , что противоречит (5). Это противоречие завершает доказательство теоремы. , что противоречит (5). Это противоречие завершает доказательство теоремы.
Пусть  --- группа и --- группа и 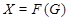 --- ее подгруппа Фиттинга. Тогда --- ее подгруппа Фиттинга. Тогда  является сверхразрешимой в том и только том случае, когда является сверхразрешимой в том и только том случае, когда 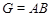 , где , где  и и  --- такие сверхразрешимые подгруппы группы --- такие сверхразрешимые подгруппы группы  , что , что 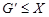 и и   -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 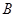 и и 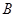  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  . .
Доказательство. Необходимость. Пусть  --- сверхразрешимая группа. Тогда ввиду леммы , --- сверхразрешимая группа. Тогда ввиду леммы ,  . Пусть . Пусть  --- минимальная нормальная подгруппа группы --- минимальная нормальная подгруппа группы  . Тогда . Тогда  для некоторого простого числа для некоторого простого числа  . Пусть . Пусть  --- такая максимальная подгруппа группы --- такая максимальная подгруппа группы  , что , что  . Тогда . Тогда 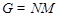 , , 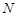 и и 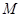 сверхразрешимы и каждая подгруппа группы сверхразрешимы и каждая подгруппа группы  перестановочна с каждой подгруппой группы перестановочна с каждой подгруппой группы  . .
Достаточность. Пусть 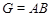 , где , где  и и 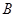 --- сверхразрешимые подгруппы, --- сверхразрешимые подгруппы,  --- подгруппа Фиттинга группы --- подгруппа Фиттинга группы  , , 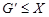 и и   -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 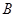 и и 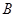  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  . Предположим, что . Предположим, что  не является сверхразрешимой группой, и пусть не является сверхразрешимой группой, и пусть 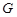 --- контрпример минимального порядка. Поскольку --- контрпример минимального порядка. Поскольку  , то , то  разрешима. Тогда: разрешима. Тогда:
(1) Для любой неединичной нормальной в  подгруппы подгруппы  факторгруппа факторгруппа  сверхразрешима. сверхразрешима.
Ясно, что 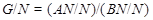 --- произведение сверхразрешимых подгрупп --- произведение сверхразрешимых подгрупп  и и  . Пусть . Пусть  и и 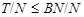 . Так как по условию для некоторых . Так как по условию для некоторых  , ,
 и и

то мы имеем


 и и

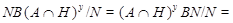

где 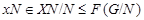 и и 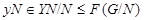 . Это показывает, что подгруппа . Это показывает, что подгруппа  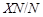 -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  и каждая подгруппа группы и каждая подгруппа группы  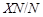 -перестановочна с подгруппой -перестановочна с подгруппой  . Но поскольку согласно лемме , . Но поскольку согласно лемме ,

то по выбору группы  мы заключаем, что мы заключаем, что  сверхразрешима. сверхразрешима.
(2) Группа  имеет единственную минимальную нормальную подгруппу имеет единственную минимальную нормальную подгруппу  и и  , где , где  --- силовская --- силовская  -подгруппа группы -подгруппа группы 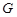 и и  --- такая максимальная в --- такая максимальная в  подгруппа, что подгруппа, что  и и 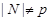 . .
Пусть 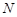 --- произвольная минимальная нормальная подгруппа группы --- произвольная минимальная нормальная подгруппа группы  . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то ввиду (1), . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то ввиду (1),  --- единственная минимальная нормальная подгруппа в --- единственная минимальная нормальная подгруппа в 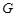 , причем , причем  . Пусть . Пусть 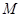 --- такая максимальная подгруппа в --- такая максимальная подгруппа в  , что , что 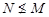 и пусть и пусть  . Тогда по тождеству Дедекинда мы имеем . Тогда по тождеству Дедекинда мы имеем  . Так как . Так как 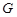 разрешима, то разрешима, то  --- элементарная абелева --- элементарная абелева  -группа для некоторого простого -группа для некоторого простого  и поэтому и поэтому  и и  . Значит, . Значит,
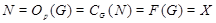 . .
Следовательно,  --- сверхразрешимая группа и ввиду леммы --- сверхразрешимая группа и ввиду леммы  . .
Так как  , то , то  абелева. Поскольку абелева. Поскольку  --- неприводимая абелева группа автоморфизмов группы --- неприводимая абелева группа автоморфизмов группы 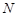 , то , то 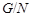 --- циклическая группа. Ввиду леммы , --- циклическая группа. Ввиду леммы ,  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Согласно (1) и выбора группы . Согласно (1) и выбора группы 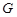 , мы имеем , мы имеем 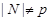 . .
(3)  или или  . .
Допустим, что  и и 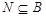 . Пусть . Пусть 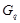 --- силовская --- силовская  -подгруппа группы -подгруппа группы 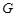 , где , где  . Тогда . Тогда 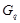 --- циклическая группа. Ввиду леммы , --- циклическая группа. Ввиду леммы , 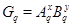 , где , где 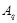 и и  --- силовские --- силовские  -подгруппы групп -подгруппы групп  и и  соответственно и соответственно и  . Тогда либо . Тогда либо  , либо , либо 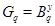 . Пусть, например, . Пусть, например, 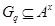 . Так как . Так как  , то , то 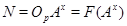 . Поскольку . Поскольку  сверхразрешима, то ввиду леммы , сверхразрешима, то ввиду леммы ,  . Тогда . Тогда 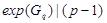 . Так как . Так как 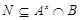 , то , то 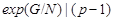 . Это показывает, что . Это показывает, что  --- абелева группа экспоненты, делящей --- абелева группа экспоненты, делящей  , и ввиду леммы , , и ввиду леммы ,  сверхразрешима, что противоречит выбору группы сверхразрешима, что противоречит выбору группы  . Значит, либо . Значит, либо  , либо , либо 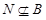 . .
(4) Заключительное противоречие.
Пусть 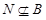 . Тогда . Тогда  . Так как . Так как  сверхразрешима, то в группе сверхразрешима, то в группе  содержится минимальная нормальная подгруппа содержится минимальная нормальная подгруппа  простого порядка простого порядка  . .
Предположим, что  . Пусть . Пусть  --- холлова --- холлова 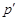 -подгруппа группы -подгруппа группы  . Тогда для некоторого . Тогда для некоторого  , ,  . Поскольку . Поскольку
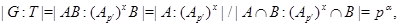
для некоторого  , то , то 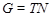 . Пусть . Пусть  . Тогда . Тогда  и и  , что противоречие (2). Значит, , что противоречие (2). Значит,  Пусть Пусть 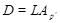 и и  для некоторого для некоторого  . Поскольку . Поскольку  и и  , то , то  , что невозможно в силу (2). Этим завершается доказательство теоремы. , что невозможно в силу (2). Этим завершается доказательство теоремы.
Пусть  --- группа и --- группа и  --- ее подгруппа Фиттинга. Тогда --- ее подгруппа Фиттинга. Тогда  является сверхразрешимой в том и только том случае, когда является сверхразрешимой в том и только том случае, когда  , где , где  и и  --- такие сверхразрешимые подгруппы взаимно простых порядков, что --- такие сверхразрешимые подгруппы взаимно простых порядков, что  и каждая подгруппа группы и каждая подгруппа группы  простого порядка или порядка 4 наследственно простого порядка или порядка 4 наследственно  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  , ,  и каждая подгруппа группы и каждая подгруппа группы  простого порядка или порядка 4 наследственно простого порядка или порядка 4 наследственно  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы 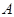 . .
Доказательство. Необходимость. Пусть  --- сверхразрешимая группа. Пусть --- сверхразрешимая группа. Пусть 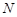 --- минимальная нормальная подгруппа группы --- минимальная нормальная подгруппа группы  . Тогда для некоторого простого . Тогда для некоторого простого 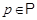 , ,  . Пусть . Пусть 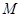 --- максимальная подгруппа группы --- максимальная подгруппа группы  такая, что такая, что 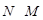 . Тогда . Тогда 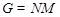 и и  перестановочна с каждой подгруппой группы перестановочна с каждой подгруппой группы  . .
Достаточность. Предположим, что  --- произведение подгрупп --- произведение подгрупп 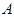 и и  , где , где  , ,  --- сверхразрешимы подгруппы взаимно простых порядков, --- сверхразрешимы подгруппы взаимно простых порядков,  --- подгруппа Фиттинга группы --- подгруппа Фиттинга группы  , ,  и каждая подгруппа группы и каждая подгруппа группы  простого порядка или порядка 4 наследственно простого порядка или порядка 4 наследственно  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  , ,  и каждая подгруппа группы и каждая подгруппа группы  простого порядка или порядка 4 наследственно простого порядка или порядка 4 наследственно  -перестановочна с каждой подгруппой группы -перестановочна с каждой подгруппой группы  . Предположим, что . Предположим, что  не является сверхразрешимой группой, и пусть не является сверхразрешимой группой, и пусть  --- контрпример минимального порядка. Доказательство разобьем на следующие этапы. --- контрпример минимального порядка. Доказательство разобьем на следующие этапы.
(1) В группе  имеется несверхразрешимая максимальная подгруппа. имеется несверхразрешимая максимальная подгруппа.
Предположим, что каждая максимальная подгруппа группы  сверхразрешима. Тогда ввиду леммы , сверхразрешима. Тогда ввиду леммы ,  разрешима. Согласно леммы , для некоторого разрешима. Согласно леммы , для некоторого 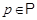 в группе в группе  имеется нормальная силовская имеется нормальная силовская  -подгруппа -подгруппа  , удовлетворяющая следующим условиям: , удовлетворяющая следующим условиям:
(i)  свехразрешима и свехразрешима и  --- наименьшая нормальная подгруппа группы --- наименьшая нормальная подгруппа группы  , факторгруппа по которой сверхразрешима; , факторгруппа по которой сверхразрешима;
(ii) если  то то  ; если ; если  то экспонента подгруппы то экспонента подгруппы 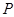 равна 2 или 4; равна 2 или 4;
(iii)  --- главный фактор группы --- главный фактор группы  . .
Допустим, что 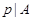 . Тогда . Тогда  . Пусть . Пусть  и пусть и пусть  --- такое простое число, что --- такое простое число, что 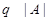 , , 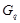 --- силовская --- силовская  -подгруппа группы -подгруппа группы 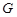 . Пусть . Пусть  --- такая холлова --- такая холлова  -подгруппа группы -подгруппа группы  , что , что 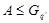 . Тогда . Тогда  . Поскольку . Поскольку  , то , то  содержится в некоторой максимальной подгруппе группы содержится в некоторой максимальной подгруппе группы  . Так как каждая максимальная подгруппа группы . Так как каждая максимальная подгруппа группы  сверхразрешима, то сверхразрешима, то 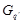 сверхразрешима. Значит, в группе сверхразрешима. Значит, в группе  имеется такая нормальная подгруппа имеется такая нормальная подгруппа 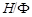 , что , что  и поэтому и поэтому  , где , где 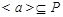 . Следовательно, . Следовательно, 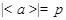 или или  . Для некоторого . Для некоторого  , мы имеем , мы имеем 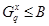 . Тогда по условию, . Тогда по условию,  . Поскольку . Поскольку  субнормальна в субнормальна в  и и 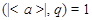 , то , то  , и поэтому , и поэтому  . Следовательно, . Следовательно,  --- циклическая группа. Так как --- циклическая группа. Так как  --- сверхразрешимая группа, то --- сверхразрешимая группа, то 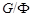 сверхразрешима. Значит, сверхразрешима. Значит,  --- сверхразрешимая группа. Это противоречие с выбором группы --- сверхразрешимая группа. Это противоречие с выбором группы  доказывает (1). доказывает (1).
(2) Группа  не является разрешимой. не является разрешимой.
Допустим, что  разрешима и пусть разрешима и пусть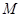 --- произвольная максимальная подгруппа группы --- произвольная максимальная подгруппа группы  . Тогда . Тогда  для некоторого простого для некоторого простого  . Без ограничения общности мы можем предположить, что . Без ограничения общности мы можем предположить, что  . Согласно теоремы , . Согласно теоремы ,  для некоторого для некоторого  . Покажем, что . Покажем, что  сверхразрешима. Используя тождество Дедекинда, получаем сверхразрешима. Используя тождество Дедекинда, получаем  , где , где  и и  --- сверхразрешимые подгруппы группы --- сверхразрешимые подгруппы группы  взаимно простых порядков. Пусть взаимно простых порядков. Пусть 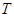 --- произвольная подгруппа группы --- произвольная подгруппа группы  простого порядка или порядка 4. И пусть простого порядка или порядка 4. И пусть  --- подгруппа группы --- подгруппа группы  . Тогда по условию . Тогда по условию 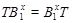 для некоторого для некоторого  . Поскольку . Поскольку  , то , то  . Значит, теорема справедлива для . Значит, теорема справедлива для  и ее подгрупп и ее подгрупп 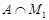 и и  . Так как . Так как  , то по выбору группы , то по выбору группы  , заключаем, что подгруппа , заключаем, что подгруппа  сверхразрешима, и поэтому сверхразрешима, и поэтому  тоже сверхразрешима. Следовательно, каждая максимальная подгруппа группы тоже сверхразрешима. Следовательно, каждая максимальная подгруппа группы  сверхразрешима, что невозможно в силу (1). Этим доказано (2). сверхразрешима, что невозможно в силу (1). Этим доказано (2).
(3) Группа  имеет нормальную силовскую подгруппу. имеет нормальную силовскую подгруппу.
Пусть 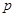 --- наибольший простой делитель --- наибольший простой делитель  . Без ограничения общности, мы можем предположить, что . Без ограничения общности, мы можем предположить, что 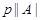 . Пусть . Пусть 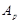 --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Так как по условию, . Так как по условию,  сверхразрешима, то ввиду леммы , сверхразрешима, то ввиду леммы ,  . Пусть . Пусть  --- силовская --- силовская  -подгруппа группы -подгруппа группы  , где , где  . Тогда для некоторого . Тогда для некоторого 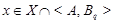 , , 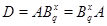 . Предположим, что . Предположим, что  . Согласно леммы , . Согласно леммы ,  и поэтому и поэтому  . Тогда для некоторого . Тогда для некоторого 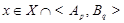 , , 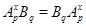 . Если . Если  , то по теореме Бернсайда, , то по теореме Бернсайда,  разрешима, что невозможно в силу (2). Значит, разрешима, что невозможно в силу (2). Значит,  . Так как теорема справедлива для группы . Так как теорема справедлива для группы 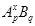 , то по выбору группы , то по выбору группы  , мы заключаем, что группа , мы заключаем, что группа 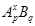 сверхразрешима. Это влечет сверхразрешима. Это влечет  . Следовательно, . Следовательно,  . .
(4) Заключительное противоречие.
Пусть  --- нормальная силовская подгруппа группы --- нормальная силовская подгруппа группы 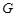 . Тогда . Тогда  для некоторых для некоторых 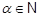 и и  . Без ограничения общности, мы можем предположить, что . Без ограничения общности, мы можем предположить, что  . Покажем, что теорема справедлива для . Покажем, что теорема справедлива для
 . .
Подгруппы  и и  являются сверхразрешимыми подгруппами группы являются сверхразрешимыми подгруппами группы  взаимно простых порядков. Предположим, что взаимно простых порядков. Предположим, что  . Пусть . Пусть  --- произвольная подгруппа группы --- произвольная подгруппа группы  простого порядка (порядка 2 или 4, в случае, когда простого порядка (порядка 2 или 4, в случае, когда  ). Тогда по теореме Шура-Цассенхауза , группа ). Тогда по теореме Шура-Цассенхауза , группа  имеет такую подгруппу имеет такую подгруппу 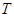 , что , что  и и 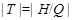 . Пусть . Пусть  --- подгруппа группы --- подгруппа группы  . Используя тождество Дедекинда, мы имеем . Используя тождество Дедекинда, мы имеем  . По условию для некоторого . По условию для некоторого 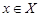 , ,  и поэтому и поэтому


Поскольку  , то , то  . Значит, теорема справедлива для группы . Значит, теорема справедлива для группы  , и поэтому , и поэтому  разрешима. Следовательно, разрешима. Следовательно,  --- разрешимая группа, что невозможно в силу (2). Этим противоречием завершается доказательство теоремы. --- разрешимая группа, что невозможно в силу (2). Этим противоречием завершается доказательство теоремы.
2. Факторизуемые группы с 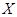 -перестановочными силовскими подгруппами -перестановочными силовскими подгруппами
Строение конечной группы тесно связано с условиями, налагаемыми на силовские подгруппы некоторых выделенных подгрупп этой группы. Отметим, в частности, что в работе Хупперта, было доказано, что разрешимая группа  является свехразрешимой, если все максимальные подгруппы всех силовских подгрупп из является свехразрешимой, если все максимальные подгруппы всех силовских подгрупп из 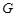 перестановочны со всеми членами некоторой силовской системы группы перестановочны со всеми членами некоторой силовской системы группы 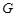 . Целью данного раздела является дальнейшее изучение строения факторизуемых групп, у которых силовские подгруппы некоторой выделенной подгруппы группы перестановочны или . Целью данного раздела является дальнейшее изучение строения факторизуемых групп, у которых силовские подгруппы некоторой выделенной подгруппы группы перестановочны или  -перестановочны с некоторой системой ее подгрупп. -перестановочны с некоторой системой ее подгрупп.
Пусть  --- разрешимая группа и --- разрешимая группа и  --- произведение --- произведение 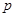 -сверхразрешимых подгрупп -сверхразрешимых подгрупп  и и  взаимно простого порядка. Предположим, что взаимно простого порядка. Предположим, что  делит порядок подгруппы делит порядок подгруппы  и и
(1) если  , то , то 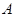 и каждая ее подгруппа простого порядка и каждая ее подгруппа простого порядка  перестановочна с каждой силовской подгруппой группы перестановочна с каждой силовской подгруппой группы  ; ;
(2) если  , то , то  и каждая ее подгруппа порядка 2 и 4 перестановочна с каждой силовской подгруппой группы и каждая ее подгруппа порядка 2 и 4 перестановочна с каждой силовской подгруппой группы  . .
Тогда  --- --- 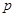 -сверхразрешимая группа. -сверхразрешимая группа.
Доказательство. Предположим, что теорема неверна и пусть  --- контрпример наименьшего порядка. Пусть --- контрпример наименьшего порядка. Пусть  --- класс всех --- класс всех 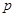 -сверхразрешимых групп. -сверхразрешимых групп.
Пусть 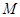 --- --- 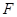 -абнормальная максимальная в -абнормальная максимальная в  подгруппа. Тогда подгруппа. Тогда 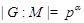 для некоторого для некоторого  или или 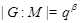 для некоторого для некоторого 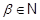 и и  . Предположим сначала, что . Предположим сначала, что 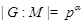 . Поскольку . Поскольку 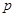 делит делит  и согласно теоремы Холла, и согласно теоремы Холла,  имеет такой элемент имеет такой элемент  , что , что  , то без ограничения общности мы можем предположить, что , то без ограничения общности мы можем предположить, что  . Покажем, что . Покажем, что 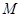 --- ---  -сверхразрешимая группа. Используя тождество Дедекинда, мы имеем -сверхразрешимая группа. Используя тождество Дедекинда, мы имеем 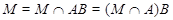 , где , где  и и   -сверхразрешимые подгруппы группы -сверхразрешимые подгруппы группы 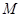 взаимно простых порядков. Если взаимно простых порядков. Если 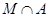 является является 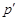 -подгруппой, то -подгруппой, то 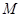 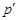 -группа и поэтому -группа и поэтому   -сверхразрешима. Предположим теперь, что -сверхразрешима. Предположим теперь, что  . Пусть . Пусть 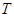 --- произвольная подгруппа группы --- произвольная подгруппа группы 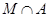 простого порядка простого порядка  (или 4, в случае, если (или 4, в случае, если  ). И пусть ). И пусть 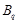 --- силовская --- силовская 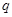 -подгруппа группы -подгруппа группы  . Тогда по условию, . Тогда по условию,  и поскольку и поскольку 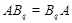 , то , то 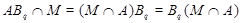 . Итак, теорема справедлива для группы . Итак, теорема справедлива для группы  и ее подгрупп и ее подгрупп  и и  . Но . Но  и поэтому согласно выбора группы и поэтому согласно выбора группы 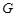 , мы заключаема, что группа , мы заключаема, что группа 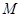  -сверхразрешима. Пусть теперь, -сверхразрешима. Пусть теперь,  , где , где 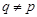 . Рассуждая как выше, мы можем показать, что . Рассуждая как выше, мы можем показать, что 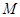 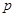 -сверхразрешима. Следовательно, каждая -сверхразрешима. Следовательно, каждая  -абнормальная максимальная в -абнормальная максимальная в  подгруппа подгруппа  -сверхразрешима. -сверхразрешима.
Так как  разрешима, то ввиду леммы , разрешима, то ввиду леммы , 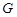 имеет нормальную имеет нормальную  -подгруппу -подгруппу 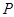 , удовлетворяющую следующим условиям: , удовлетворяющую следующим условиям:
(i) 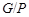 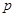 -сверхразрешима и -сверхразрешима и  наименьшая нормальная подгруппа группы наименьшая нормальная подгруппа группы  , факторгруппа по которой , факторгруппа по которой  -сверхразрешима; -сверхразрешима;
(ii) если  то экспонента подгруппы то экспонента подгруппы 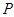 равна равна  ; если ; если 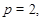 то экспонента подгруппы то экспонента подгруппы  равна 2 или 4; равна 2 или 4;
(iii) 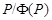 --- главный фактор группы --- главный фактор группы  . .
Ясно, что  . Пусть . Пусть  и пусть и пусть  --- такое простое число, что --- такое простое число, что  , ,  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Пусть . Пусть  --- некоторая такая холлова --- некоторая такая холлова  -подгруппа группы -подгруппа группы  , что , что  . Тогда . Тогда  . Рассуждая как выше, видим, что . Рассуждая как выше, видим, что   -сверхразрешима. Тогда в группе -сверхразрешима. Тогда в группе  имеется такая нормальная подгруппа имеется такая нормальная подгруппа  , что , что  и поэтому и поэтому  , где , где  . Ясно, что . Ясно, что  или или  . Согласно лемме , для некоторого . Согласно лемме , для некоторого  , мы имеем , мы имеем  . Тогда по условию, . Тогда по условию, 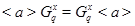 . Так как . Так как  субнормальна в субнормальна в  и и  , то , то  , и поэтому , и поэтому 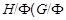 . Следовательно, . Следовательно,  --- циклическая группа. Ясно, что --- циклическая группа. Ясно, что   -сверхразрешима и поэтому -сверхразрешима и поэтому   -сверхразрешима, противоречие. Теорема доказана. -сверхразрешима, противоречие. Теорема доказана.
Прежде, чем дать доказательство следующего основного результата этого раздела, нам необходимо установить справедливость следующей леммы.
Пусть  --- простое число, --- простое число,  , где , где 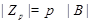 , ,  --- разрешимая группа, --- разрешимая группа,   -перестановочна с каждой силовской подгруппой группы -перестановочна с каждой силовской подгруппой группы  , где , где  --- подгруппа Фиттинга группы --- подгруппа Фиттинга группы  . Тогда . Тогда  разрешима. разрешима.
Доказательство. Предположим, что эта лемма не верна и пусть группа 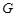 --- контрпример минимального порядка. Тогда: --- контрпример минимального порядка. Тогда:
(1)  не простая группа
. не простая группа
.
Предположим, что  --- простая группа. Тогда --- простая группа. Тогда  . Пусть . Пусть 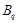 --- силовская --- силовская 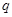 -подгруппа группы -подгруппа группы  . Тогда по условию . Тогда по условию  . Действительно, поскольку для каждого . Действительно, поскольку для каждого  мы имеем мы имеем

где 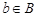 и и 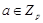 . Тогда ввиду леммы , . Тогда ввиду леммы ,  непроста. непроста.
(2) 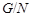 --- разрешимая группа для каждой неединичной нормальной подгруппы --- разрешимая группа для каждой неединичной нормальной подгруппы  группы группы  . .
Пусть  --- неединичная нормальная подгруппа группы --- неединичная нормальная подгруппа группы  . Если . Если  , то , то  разрешима. разрешима.
Пусть  . Тогда . Тогда 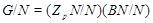 --- произведение подгруппы --- произведение подгруппы  простого порядка простого порядка  и разрешимой группы и разрешимой группы  . Пусть . Пусть  --- силовская --- силовская 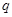 -подгруппа группы -подгруппа группы 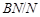 . Тогда . Тогда  для некоторой силовской для некоторой силовской  -подгруппы -подгруппы  группы группы  , и поэтому по условию, , и поэтому по условию,

для некоторого  . Итак, теорема справедлива для факторгруппы . Итак, теорема справедлива для факторгруппы 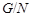 . Но . Но  , и поэтому ввиду выбора группы , и поэтому ввиду выбора группы 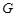 , факторгруппа , факторгруппа  разрешима. разрешима.
(3) Заключительное противоречие.
Если 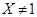 , то ввиду (2), , то ввиду (2),  разрешима и поэтому разрешима и поэтому 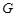 --- разрешимая группа, противоречие. Значит, --- разрешимая группа, противоречие. Значит,  . Путсь . Путсь  --- минимальная нормальная подгруппа группы --- минимальная нормальная подгруппа группы  . Тогда ввиду (1), . Тогда ввиду (1),  . Допустим, что . Допустим, что 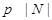 . Тогда . Тогда  . Так как по условию, . Так как по условию,  разрешима, то разрешима, то  разрешима и поэтому согласно (2), разрешима и поэтому согласно (2), 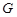 --- разрешимая группа, противоречие. Следовательно, --- разрешимая группа, противоречие. Следовательно, 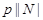 . Поскольку . Поскольку  --- холлова --- холлова  -подгруппа группы -подгруппа группы  , то , то 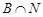 --- холлова --- холлова 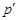 -подгруппа группы -подгруппа группы 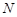 . Ясно, что . Ясно, что  , и по тождеству Дедекинда, , и по тождеству Дедекинда, 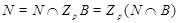 . Путсь . Путсь  --- силовская --- силовская 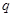 -подгруппа группы -подгруппа группы  , , 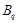 --- силовская --- силовская  -подгруппа группы -подгруппа группы  такая, что такая, что  . Тогда по условию, . Тогда по условию,  , и поэтому , и поэтому  . Следовательно, теорема справедлива для группы . Следовательно, теорема справедлива для группы 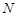 и поэтому и поэтому 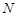 разрешима. Следовательно, разрешима. Следовательно, 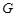 --- разрешимая группа, противоречие с выбором группы --- разрешимая группа, противоречие с выбором группы  . Лемма доказана. . Лемма доказана.
Пусть  --- группа и --- группа и  --- ее подгруппа Фиттинга. Если --- ее подгруппа Фиттинга. Если 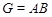 , где , где 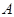 и и  --- сверхразрешимые подгруппы группы --- сверхразрешимые подгруппы группы  , каждай примарная циклическая погруппа группы , каждай примарная циклическая погруппа группы  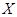 -перестановочна с каждой силовской подгруппой группы -перестановочна с каждой силовской подгруппой группы  и каждай примарная циклическая погруппа группы и каждай примарная циклическая погруппа группы  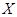 -перестановочна с каждой силовской подгруппой группы -перестановочна с каждой силовской подгруппой группы  , то , то  сверхразрешима. сверхразрешима.
Доказательство. Предположим, что теорема неверна и пусть  --- минимальный контрпример. Тогда: --- минимальный контрпример. Тогда:
(1) Для каждой нормальной неединичной подгруппы  в в  фактогруппа фактогруппа 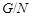 сверхразрешима. сверхразрешима.
Пусть  --- неединичная нормальная подгруппа в --- неединичная нормальная подгруппа в 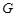 . Заметим, что . Заметим, что  --- произведение сверхразрешимых подгрупп --- произведение сверхразрешимых подгрупп 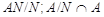 и и 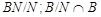 . Пусть . Пусть  --- примарная циклическая подгруппа группы --- примарная циклическая подгруппа группы  . Ясно, что для некоторой примарной циклической подгруппы . Ясно, что для некоторой примарной циклической подгруппы  группы группы  , , 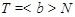 . Поскольку . Поскольку  , то , то  для некоторого для некоторого 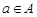 , имеющего примарный порядок и для некоторого , имеющего примарный порядок и для некоторого  , и поэтому , и поэтому  . Пусть . Пусть 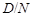 --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Тогда . Тогда  для некоторой силовской для некоторой силовской  -подгруппы -подгруппы 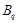 группы группы  . Так как по условию, для некоторого . Так как по условию, для некоторого 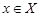 , ,  и поэтому и поэтому



Ясно, что 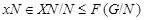 . Итак, теорема справедлива для . Итак, теорема справедлива для 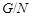 . Но . Но  , и ввиду выбора группы , и ввиду выбора группы  , мы имеем (1). , мы имеем (1).
(2)  разрешима. разрешима.
Допустим, что  не является разрешимой группой. не является разрешимой группой.
Если  , то ввиду (1), , то ввиду (1),  сверхразрешима и поэтому сверхразрешима и поэтому 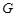 разрешима, противоречие с выбором группы разрешима, противоречие с выбором группы  . Следовательно, . Следовательно, 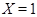 . Пусть . Пусть  --- наибольший простой делитель --- наибольший простой делитель 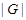 . Без ограничения общности, мы можем предположить, что . Без ограничения общности, мы можем предположить, что  . Пусть . Пусть 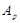 --- --- 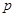 -подгруппа группы -подгруппа группы  . Тогда по условию, . Тогда по условию, 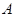 сверхразрешима. Ввиду леммы , сверхразрешима. Ввиду леммы ,  . Следовательно, . Следовательно,  имеет такую минимальную нормальную подгруппу, скажем имеет такую минимальную нормальную подгруппу, скажем  , что , что  . Если . Если  , то ввиду леммы , , то ввиду леммы ,  . Поскольку теорема справедлива для . Поскольку теорема справедлива для  , то , то  сверхразрешима и поэтому минимальная нормальная подгруппа группы сверхразрешима и поэтому минимальная нормальная подгруппа группы  , которая содержится в , которая содержится в 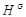 , абелева. Ввиду (1), , абелева. Ввиду (1), 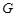 разрешима, противоречие. Пусть разрешима, противоречие. Пусть  и пусть и пусть 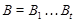 , где , где  --- силовские подгруппы группы --- силовские подгруппы группы  . Тогда по условию, . Тогда по условию,  перестановочна со всеми перестановочна со всеми  , ,  . Допустим, что . Допустим, что  . Поскольку теорема справедлива для . Поскольку теорема справедлива для  и и  , то мы заключаем, что , то мы заключаем, что  сверхразрешима. Но сверхразрешима. Но 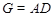 , и поэтому ввиду леммы и (1), мы снова приходим к противоречию. Допустим теперь, что , и поэтому ввиду леммы и (1), мы снова приходим к противоречию. Допустим теперь, что  . Ввиду леммы , мы можем предположить, что . Ввиду леммы , мы можем предположить, что  . Пусть . Пусть  --- силовская --- силовская  -подгруппа группы -подгруппа группы  . Тогда . Тогда 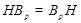 , и , и  . Поскольку . Поскольку  , то , то  , и поэтому ввиду (1), , и поэтому ввиду (1),  разрешима, противоречие. Это доказывает (2). разрешима, противоречие. Это доказывает (2).
(3)  имеет единственную минимальную нормальную подгруппу имеет единственную минимальную нормальную подгруппу 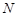 и и 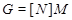 , где , где 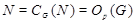 для некоторого простого числа для некоторого простого числа 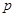 , ,  сверхразрешимая максимальная подгруппа группы сверхразрешимая максимальная подгруппа группы  и и 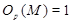 . .
Пусть  --- произвольная минимальная нормальная подгруппа группы --- произвольная минимальная нормальная подгруппа группы 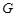 . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то ввиду (1), . Так как класс всех сверхразрешимых групп образует насыщенную формацию, то ввиду (1),  --- единственная минимальная нормальная подгруппа в --- единственная минимальная нормальная подгруппа в 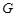 , причем , причем  . Пусть . Пусть 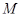 --- максимальная подгруппа группы --- максимальная подгруппа группы  , не содержащая , не содержащая  и и  . Тогда по тожеству Дедекинда, . Тогда по тожеству Дедекинда,  Так как ввиду (2), Так как ввиду (2),  абелева, то абелева, то  и поэтому и поэтому  . Следовательно, . Следовательно,  и и  сверхразрешима и согласно леммы , сверхразрешима и согласно леммы , 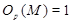 . .
(4)  --- наибольший простой делитель порядка группы --- наибольший простой делитель порядка группы  . .
Пусть  и и  --- такие максимальные подгруппы группы --- такие максимальные подгруппы группы 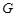 , что , что  , ,  . Так как . Так как  , то ввиду леммы , , то ввиду леммы ,  для некоторого для некоторого  . Поскольку ввиду леммы , . Поскольку ввиду леммы ,  , то либо , то либо  , либо , либо  . Пусть . Пусть  . И пусть . И пусть 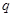 --- наибольший простой делитель --- наибольший простой делитель  . Тогда силовская . Тогда силовская  -подгруппа группы -подгруппа группы  нормальна в нормальна в  , и поэтому , и поэтому  содержится в содержится в 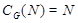 . Следовательлно, . Следовательлно, 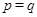 --- наибольший простой делитель --- наибольший простой делитель  . Если . Если  не является холловой подгруппой группы не является холловой подгруппой группы  ,то справедливо (4). Пусть ,то справедливо (4). Пусть  --- холлова подгруппа группы --- холлова подгруппа группы  и допустим, что и допустим, что  , где , где  наибольший простой делитель порядка группы наибольший простой делитель порядка группы  . Тогда . Тогда  для некоторого для некоторого 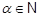 . Так как . Так как  , то ввиду (1), , то ввиду (1),  порядок силовской порядок силовской 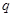 -подгруппы группы -подгруппы группы  . Ясно, что . Ясно, что  . Пусть . Пусть 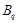 --- силовская --- силовская  -подгруппа группы -подгруппа группы  . По условию, . По условию,  для некоторого для некоторого 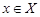 и ввиду леммы , и ввиду леммы ,  . Согласно леммы , . Согласно леммы ,  . Поскольку . Поскольку  , то , то  имеет нормальную подгруппу имеет нормальную подгруппу 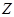 простого порядка простого порядка  такую, что такую, что 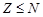 и и  для некоторого для некоторого 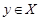 . Согласно леммы , . Согласно леммы , 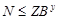 , и поэтому ввиду (2), , и поэтому ввиду (2), 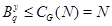 , противоречие. Полученное противоречие доказывает (4). , противоречие. Полученное противоречие доказывает (4).
(5)  --- силовская --- силовская  -подгруппа группы -подгруппа группы 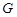 . .
Допустим, что это утверждение не верно. Тогда 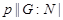 . Это влечет . Это влечет  и поэтому ввиду (4), и леммы, и поэтому ввиду (4), и леммы,  , что противоречит (3). Итак, , что противоречит (3). Итак, 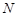 --- силовская --- силовская  -подгруппа группы -подгруппа группы 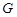 . .
(6) Заключительное противоречие.
Поскольку  и и  --- силовская --- силовская  -подгруппа группы -подгруппа группы 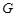 , то либо , то либо  , либо , либо 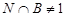 . Допустим, что . Допустим, что 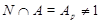 и пусть и пусть  --- минимальная нормальная в --- минимальная нормальная в  подгруппа, содержащаяся в подгруппа, содержащаяся в  . .
По условию, 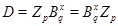 для некоторого для некоторого 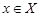 , где , где  --- некоторое простое число, --- некоторое простое число,  и и  --- холлова --- холлова  -подгруппа группы -подгруппа группы  . Тогда . Тогда

Значит, 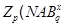 и поэтому и поэтому  . Таким образом, . Таким образом,  . Следовательно, . Следовательно, 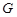 --- сверхразрешимая группа, что противоречит выбору группы --- сверхразрешимая группа, что противоречит выбору группы 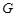 . Теорема доказана. . Теорема доказана.
Заключение
В данной главе получены новые критерии сверхразрешимости факторизуемых групп на основе условия  -перестановочности некоторых подгрупп. Полученные здесь результаты показывают, что строение группы в существенной мере определяется наличием в ней факторизаций системами перестановочных и -перестановочности некоторых подгрупп. Полученные здесь результаты показывают, что строение группы в существенной мере определяется наличием в ней факторизаций системами перестановочных и  -перестановочных подгрупп.
Пальчик Э.М., Конторович Н.П. О группах, все -перестановочных подгрупп.
Пальчик Э.М., Конторович Н.П. О группах, все  -максимальные подгруппы которых перестановочны с силовской подгруппой. -максимальные подгруппы которых перестановочны с силовской подгруппой.
Литература
1.Подгорная В.В. Полунормальные подгруппы и сверхразрешимость конечных групп // Весцi НАН Беларусi. Сер. фiз.-матэм. навук. --- 2000. --- № 4. --- С. 22---25.
2.Подгорная В.В. Факторизации конечных групп дисперсивными и сверхразрешимыми подгруппами // Веснiк Вiцебскага дзяржаунага Унiверсiтэта. --- 1999. --- № 4(14). --- С. 80---82.
3.Поляков Л.Я. Конечные группы с перестановочными подгруппами // Конечные группы. --- Минск: Наука и техника, 1966. --- С.75---88.
4.Самусенко (Подгорная) В.В. О конечных группах с заданными минимальными добавлениями к подгруппам // Вопросы алгебры. Выпуск 13. --- 1998. --- С. 177---182.
5.Самусенко (Подгорная) В.В. О сверхразрешимости конечных групп с циклическими добавлениями к подгруппам // Вопросы алгебры. Выпуск 14. --- 1999. --- С. 141---146.
6.Сергиенко В.И. Критерий  -разрешимости для конечных групп // Мат. заметки. --- 1971. --- Т. 9, № 4. --- С. 375---383. -разрешимости для конечных групп // Мат. заметки. --- 1971. --- Т. 9, № 4. --- С. 375---383.
7.Сергиенко В.И. Некоторые свойства квазинормальных групп // Подгрупповое строение конечных групп: труды гомельского семинара / Под ред. В.С. Монахова. --- Мн.: Наука и техника, 1981. --- С.149---152.
8.Скиба А.Н.  -перестановочные подгруппы // Известия Гомельского государственного университета имени Ф.Скорины. --- 2003. --- № 4(19). --- C. 37---39. -перестановочные подгруппы // Известия Гомельского государственного университета имени Ф.Скорины. --- 2003. --- № 4(19). --- C. 37---39.
9.Черников Н.С. Группы, разложимые в произведение перестановочных подгрупп. --- Киев: Наук. думка, 1987. ---208с.
10.Черток В.Д. Порождение конечной группы системами недостижимых подгрупп // ИАН БССР. Сер. физ.-матем. наук. --- 1967. --- № 2. --- С. 80---84.
11.Чунихин С.А. Об условиях теорем типа Силова // ДАН СССР. --- 1949. --- Т. 69, № 6. --- С. 735---737.
12.Чунихин С.А. Подгруппы конечных групп. --- Минск: Наука и техника, 1964. --- 158 с.
13.Шеметков Л.А. Формации конечных групп. --- М.: Наука, 1978.--- 272 с.
14.Шмидт О.Ю. Группы, все подгруппы которых специальные // Мат. сб. --- 1924. --- Т. 31. --- С. 366---372.
|