| Курсовая работа
"Представления конечных групп"
Содержание
Основные обозначения
Введение
1. Представления конечных групп
1.1 Представления групп
1.2 Представления унитарными матрицами и полная приводимость представлений конечных групп
1.3 Лемма Шура
1.4 Соотношения ортогональности для характеров
1.5 Индуцированные представления
1.6 Произведение представлений
Заключение
Список использованных источников
Основные обозначения
Введение
В данной работе приведены доказательства следующих теорем:
Теорема.
Непустое подмножество 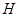 группы группы  будет подгруппой тогда и только тогда, когда будет подгруппой тогда и только тогда, когда  и и  для всех для всех  .
.
Группой
называется непустое множество  с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием: с бинарной алгебраической операцией (умножением), которая удовлетворяет следующим требованием:
1) операция определена на  , т.е. , т.е.  для всех для всех 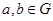 ; ;
2) операция ассоциативна, т.е. 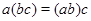 для любых для любых 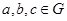 ; ;
3) в  существует единичный элемент, т.е. такой элемент существует единичный элемент, т.е. такой элемент  , что , что  для всех для всех  , что , что  для всех для всех  ; ;
4) каждый элемент обладает обратным, т.е. для любого  существует такой элемент существует такой элемент 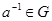 , что , что  . .
Более кратко: полугруппа с единицей, в которой каждый элемент обладает обратным, называется группой
.
Группу с коммутативной операцией называют коммутативной
или абелевой
. Если  – конечное множество, являющиеся группой, то – конечное множество, являющиеся группой, то  называют конечной группой
, а число называют конечной группой
, а число 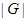 элементов в элементов в  – порядком группы – порядком группы
 . .
Подмножество 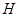 группы группы  называется подгруппой
, если называется подгруппой
, если 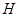 – группа относительно той же операции, которая определена на – группа относительно той же операции, которая определена на  . Запись . Запись 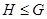 означает, что означает, что 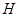 – подгруппа группы – подгруппа группы  , а , а 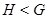 – что – что 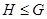 – собственная подгруппа группы – собственная подгруппа группы  , т.е. , т.е. 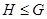 и и  . .
Централизатор
. Пусть 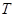 – непустое подмножество группы – непустое подмножество группы  . Совокупность всех элементов группы . Совокупность всех элементов группы  , перестановочных с каждым элементом множества , перестановочных с каждым элементом множества 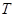 , называется централизатором множества , называется централизатором множества 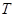 в группе в группе
 и обозначается через и обозначается через  . .
Лемма
1. Если 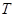 – подмножество группы – подмножество группы  , то централизатор , то централизатор  является подгруппой. является подгруппой.
2. Если  и и 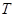 – подмножество группы – подмножество группы  и и  , то , то 
3. Если 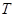 – подмножество группы – подмножество группы  и и  , то , то 
Центр группы
. Центром группы  называется совокупность всех элементов из
называется совокупность всех элементов из  , перестановочных с каждым элементом группы. Центр обозначается через , перестановочных с каждым элементом группы. Центр обозначается через  . Ясно, что . Ясно, что 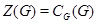 , т.е. центр группы , т.е. центр группы  совпадает с централизатором подмножества совпадает с централизатором подмножества  в группе в группе  . Кроме того, . Кроме того,  . .
Зафиксируем в группе  элемент элемент  . Пересечение всех подгрупп группы . Пересечение всех подгрупп группы  , содержащих элемент , содержащих элемент  , назовем циклической подгруппой, порожденной элементом , назовем циклической подгруппой, порожденной элементом  , и обозначим через
, и обозначим через  . .
Теорема.
Циклическая подгрупппа 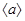 , порожденная элементом , порожденная элементом  , состоит из всевозможных целых степеней элемента , состоит из всевозможных целых степеней элемента  , т.е. , т.е. 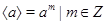
Следствие. Циклическая подгруппа абелева.
Порядок элемента.
Пусть  – элемент группы – элемент группы  . Если все степени элемента . Если все степени элемента  различны, т.е. различны, т.е.  для всех целых для всех целых  , то говорят, что элемента , то говорят, что элемента  имеет бесконечный порядок
. имеет бесконечный порядок
.
Нормализатор
. Если 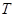 – непустое подмножество группы – непустое подмножество группы  и и  то то  и и  Элемент Элемент  называется перестановочным с подмножеством называется перестановочным с подмножеством
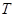 , если , если  . Равенство . Равенство  означает, что для любого элемента означает, что для любого элемента  существует такой элемент существует такой элемент  , что , что  . Если элемент . Если элемент  перестановочен с подмножеством перестановочен с подмножеством 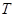 , то , то  и и  . Совокупность всех элементов группы . Совокупность всех элементов группы  , перестановочных с подмножеством , перестановочных с подмножеством 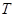 , называется нормализатором подмножества , называется нормализатором подмножества 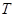 в группе в группе
 и обозначается через и обозначается через 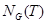 . Итак, . Итак,

Лемма.
Пусть 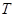 – непустое подмножество группы – непустое подмножество группы  , ,  – произвольный элемент группы – произвольный элемент группы  . Тогда: . Тогда:
1)  ; ;
2) 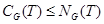 ; ;
3)  ; ;
4) 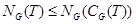 ; ;
5) если 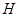 – подгруппа группы – подгруппа группы  , то , то 
Подгруппа 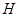 называется нормальной подгруппой
группы называется нормальной подгруппой
группы  , если , если  для всех для всех  . Запись . Запись 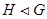 читается: » читается: » – нормальная подгруппа группы – нормальная подгруппа группы  «. Равенство «. Равенство  означает, что для любого элемента означает, что для любого элемента  существует элемент существует элемент  такой, что такой, что  . .
Теорема.
Для подгруппы  группы группы  следующие утверждения эквивалентны: следующие утверждения эквивалентны:
1) – нормальная подгруппа; – нормальная подгруппа;
2) подгруппа  вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е. вместе с каждым своим элементом содержит все ему сопряженные элементы, т.е. 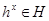 для всех для всех  ; ;
3) подгруппа  совпадает с каждой своей сопряженной подгруппой, т.е. совпадает с каждой своей сопряженной подгруппой, т.е.  для всех для всех  . .
Лемма.
Пусть  – подгруппа группы – подгруппа группы  . Тогда: . Тогда:
1) 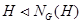 ; ;
2) если 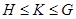 и и  , то , то  ; ;
3) 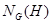 – наибольшая подгруппа группы – наибольшая подгруппа группы  , в которой , в которой 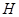 нормальна; нормальна;
4) если 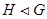 , то , то 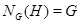 . Обратно, если . Обратно, если 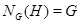 , то , то  ; ;
5)  для любого непустого подмножества для любого непустого подмножества  группы группы  . .
Простая группа
. В каждой группе  тривиальные подгруппы (единичная подгруппа тривиальные подгруппы (единичная подгруппа  и сама группа и сама группа  ) являются нормальными подгруппами. Если в неединичной группе ) являются нормальными подгруппами. Если в неединичной группе  нет других нормальных подгрупп, то группа нет других нормальных подгрупп, то группа  называется простой
. Единичную группу называется простой
. Единичную группу  считают непростой. считают непростой.
Представления конечных групп
Пусть 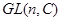 – группа всех невырожденных матриц порядка – группа всех невырожденных матриц порядка  над полем над полем 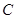 комплексных чисел. Если комплексных чисел. Если  – произвольная группа, то ее (матричным) представлением
называется любой ее гомоморфизм в – произвольная группа, то ее (матричным) представлением
называется любой ее гомоморфизм в 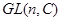
 G G , ,
такой, что
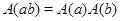 , ,
 (единичная матрица), (единичная матрица),
 . Число n называется степенью
этого представления. Если гомоморфизм A
иньективен, то представление называется точным
. . Число n называется степенью
этого представления. Если гомоморфизм A
иньективен, то представление называется точным
.
Пример 1.1
Отображение, переводящее каждый элемент группы  в в 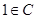 , является представлением степени , является представлением степени  . Оно называется тождественным представлением
группы . Оно называется тождественным представлением
группы  и обозначается через и обозначается через  . .
Пример 1.2
Если 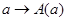 – некоторое представление группы – некоторое представление группы  , то для каждой невырожденной матрицы , то для каждой невырожденной матрицы  отображение отображение  также является представлением этой группы. также является представлением этой группы.
Пусть 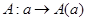 и и  – два представления группы – два представления группы  . Если существует невырожденная матрица . Если существует невырожденная матрица  , такая, что что , такая, что что
 , ,
то представления 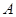 и и  называются эквивалентными
. Тот факт, что представления называются эквивалентными
. Тот факт, что представления 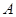 и и  эквивалентны, мы будем обозначать так: эквивалентны, мы будем обозначать так: 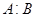 . Отношение . Отношение 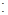 определяет классы эквивалентных представлений
группы
определяет классы эквивалентных представлений
группы  . .
Пример 1.3.
Пусть  – симметрическая группа степени – симметрическая группа степени  . Для элемента . Для элемента
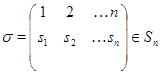
через  обозначим матрицу, обозначим матрицу,  строка которой имеет вид строка которой имеет вид  , где 1 стоит на , где 1 стоит на  месте. Другими словами, месте. Другими словами,

где

Такое отображение  является точным представлением группы является точным представлением группы  . .
1.4. Пусть  –конечная группа, состоящая из элементов –конечная группа, состоящая из элементов 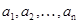 и пусть и пусть 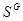 – симметрическая группа на – симметрическая группа на  . Отображение, которое ставит в соответствие элементу . Отображение, которое ставит в соответствие элементу  подстановку подстановку

является инъективным гомоморфизмом группы  в в  . С такой подстановкой . С такой подстановкой 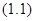 мы свяжем матрицу мы свяжем матрицу

где, как и в примере  , ,

Тогда отображение 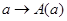 является точным представлением группы является точным представлением группы  . Оно называется правым регулярным представлением
этой группы. Определим . Оно называется правым регулярным представлением
этой группы. Определим  следующим образом: следующим образом:

Тогда

и, если  , то каждый диагональный элемент равен нулю. , то каждый диагональный элемент равен нулю.
регулярное представление группы 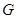 определяется аналогично с использованием гомоморфизма определяется аналогично с использованием гомоморфизма

Другими словами,

Пусть  – некоторый гомоморфизм из – некоторый гомоморфизм из 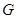 в в  , т.е. подстановочное представление группы , т.е. подстановочное представление группы 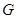 . Представив подстановку . Представив подстановку  в виде матрицы в виде матрицы  , как это сделано в примере 1.3, мы получим представление , как это сделано в примере 1.3, мы получим представление 
Пусть 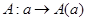 – представление степени – представление степени  . Говорят, что . Говорят, что 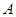 приводимо,
если существует такая невырожденная матрица приводимо,
если существует такая невырожденная матрица  , что , что

где  и и  – квадратные матрицы порядка – квадратные матрицы порядка  и и  соответственно, причем соответственно, причем 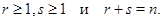 Отметим, что представления Отметим, что представления
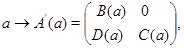

эквивалентны, поскольку  для матрицы для матрицы

Скажем, что представление  неприводимо,
если оно не является приводимым. Отметим, что в (1.3) отображения неприводимо,
если оно не является приводимым. Отметим, что в (1.3) отображения  и и  являются представлении степеней являются представлении степеней  и и  соответственно. соответственно.
Для заданных представлений  и и 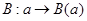 группы группы  степеней степеней  и и  соответственно отображение соответственно отображение

является представление степени  этой группы. Такое, представление называется прямой суммой
представлений этой группы. Такое, представление называется прямой суммой
представлений  и и 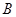 и обозначается через и обозначается через  . .
Представление  группы группы 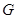 называется вполне приводимым,
если оно эквивалентно прямой сумме некоторых неприводимых представлений, т.е. если найдется невырожденная матрица называется вполне приводимым,
если оно эквивалентно прямой сумме некоторых неприводимых представлений, т.е. если найдется невырожденная матрица 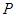 , такая, что , такая, что

где каждое  является неприводимым представлением группы является неприводимым представлением группы 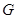 . .
Представление  группы группы 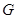 называется унитарным,
если для всех называется унитарным,
если для всех 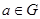 матрица матрица  является унитарной, т.е. является унитарной, т.е.  . Здесь . Здесь 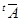 обозначает матрицу, транспонированную к обозначает матрицу, транспонированную к  , где , где  , а , а 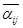 – величина, комплексно – сопряженная к – величина, комплексно – сопряженная к  . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым. . В этом параграфе мы покажем, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.
Матрица  называется эрмитовой,
если называется эрмитовой,
если  , и положительно определенной,
если , и положительно определенной,
если 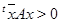 для каждого ненулевого столбца для каждого ненулевого столбца 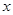 . Следующая лемма тривиальна. . Следующая лемма тривиальна.
Лемма 2.1.
Пусть  – произвольная невырожденная матрица. Тогда – произвольная невырожденная матрица. Тогда 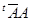 – положительно определенная эрмитова матрица. Кроме того, сумма положительно определенных эрмитовых матриц также является положительно определенной эрмитовой матрицей. – положительно определенная эрмитова матрица. Кроме того, сумма положительно определенных эрмитовых матриц также является положительно определенной эрмитовой матрицей.
Лемма 2.2.
Для любой положительно определенной эрмитовой матрицы 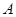 найдется невырожденная верхнетреугольная матрица найдется невырожденная верхнетреугольная матрица 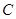 , такая, что , такая, что  . .
Доказательство. Пусть  . Тогда . Тогда  и и 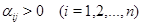 . Пусть . Пусть
 . .
Положим

Тогда

и  – положительно определенная эрмитова матрица. Для завершения доказательства достаточно воспользоваться индукцией по порядку матрицы – положительно определенная эрмитова матрица. Для завершения доказательства достаточно воспользоваться индукцией по порядку матрицы  . .
Теорема 2.3.
Пусть 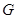 – конечная группа. Для каждого представления – конечная группа. Для каждого представления  группы группы 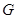 найдется невырожденная верхнетреугольная матрица найдется невырожденная верхнетреугольная матрица  , такая, что , такая, что  является унитарной матрицей для всех является унитарной матрицей для всех 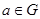 . .
Доказательство. Положим
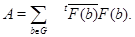
Тогда в силу леммы 2.1  является положительно определенной эрмитовой матрицей. Таким образом, найдется невырожденная верхнетреугольная матрица является положительно определенной эрмитовой матрицей. Таким образом, найдется невырожденная верхнетреугольная матрица  , такая, что , такая, что 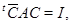 и поэтому и поэтому  . Так как . Так как
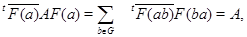
то  , т.е. , т.е.  ; поэтому ; поэтому 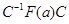 – унитарная матрица. – унитарная матрица.
Теорема 2.4.
Каждое представление конечной группы вполне приводимо.
Доказательство. Пусть  – приводимое представление конечной группы – приводимое представление конечной группы 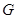 , и пусть , и пусть  разлагается следующим образом: разлагается следующим образом:
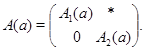
В силу предыдущей теоремы существует невырожденная матрица  , такая, что , такая, что  – унитарная матрица. Так как – унитарная матрица. Так как 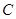 верхнетреугольная, то верхнетреугольная, то  имеет вид имеет вид

Поскольку  , мы получаем , мы получаем
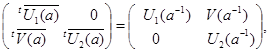
откуда следует, что  . .
Лемма 3.1.
(Лемма Шура.) Пусть  и и  – неприводимые представления группы – неприводимые представления группы 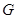 степеней степеней  и и 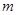 соответсвенно. Пусть соответсвенно. Пусть 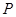 – такая – такая  – матрица, что – матрица, что

Тогда либо
 , ,
либо
 и и 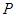 невырожденная. невырожденная.
Доказательство. Допустим, что  . Покажем, что тогда имеет место . Покажем, что тогда имеет место  . Предположим, что либо . Предположим, что либо  , либо , либо  и и 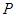 вырожденна. Тогда существуют матрицы вырожденна. Тогда существуют матрицы  и и 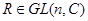 , такие, что , такие, что

где 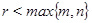 . Так как . Так как 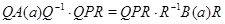 , то , то

где
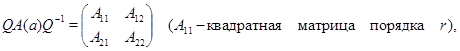

Таким образом, 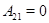 , если , если 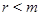 , и , и 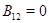 , если , если 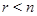 . В любом случае . В любом случае 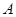 или или  приводимо, что противоречит условию. приводимо, что противоречит условию.
Теорема 3.2.
Пусть  – неприводимое представление группы – неприводимое представление группы  . Пусть . Пусть 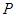 – такая матрица, что – такая матрица, что  для всех для всех 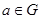 . Тогда . Тогда  , где , где  . .
Доказательство. Пусть 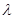 – некоторое собственное значение матрицы – некоторое собственное значение матрицы 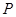 . Тогда . Тогда  , а, кроме того, , а, кроме того,

откуда в силу леммы Шура следует, что 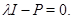
Теорема 3.3.
Пусть 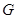 – абелева группа. Тогда каждое ее неприводимое представление имеет степень
1. – абелева группа. Тогда каждое ее неприводимое представление имеет степень
1.
Доказательство. Пусть  – неприводимое представление группы – неприводимое представление группы  . Поскольку . Поскольку  коммутирует с каждой матрицей коммутирует с каждой матрицей  , из предыдущей теоремы следует, что , из предыдущей теоремы следует, что  , где , где  . Поскольку . Поскольку  неприводимо, отсюда вытекает, что его степень равна 1. неприводимо, отсюда вытекает, что его степень равна 1.
Ниже везде предполагается, что рассматриваемые группы конечны.
Характеры.
Для квадратной матрицы  порядка порядка  обозначим через обозначим через  ее след
, т.е. ее след
, т.е.

Путем прямых вычислений доказывается следующая
Лемма 4.1.
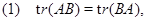
 для произвольной квадратной матрицы для произвольной квадратной матрицы 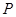 .
.
Для представления 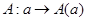 группы группы  положим положим 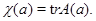 Тогда Тогда 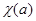 – функция, принимающая значения в множестве – функция, принимающая значения в множестве  и называемая характером
представления и называемая характером
представления  . Очевидно, что . Очевидно, что  равно степени представления равно степени представления 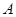 . Характеры неприводимых представлений называются неприводимыми характерами
. Из леммы 4.1 (2) вытекает следующая . Характеры неприводимых представлений называются неприводимыми характерами
. Из леммы 4.1 (2) вытекает следующая
Лемма 4.2.
Эквивалентные представления имеют один и тот же характер
.
Поскольку  , имеет место равенство , имеет место равенство  . Таким образом, . Таким образом,  принимает одно и то же значение на всем классе сопряженных элементов группы принимает одно и то же значение на всем классе сопряженных элементов группы  . Такие функции называются функциями классов
. . Такие функции называются функциями классов
.
Первое соотношение ортогональности для характеров.
Пусть  – группа порядка – группа порядка 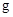 , а , а  и и  – ее неприводимые представления степеней – ее неприводимые представления степеней 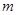 и и  соответственно. Для произвольной соответственно. Для произвольной  – матрицы – матрицы  пусть пусть

Тогда, положив  , получаем , получаем

Поскольку 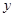 , как и , как и 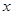 , пробегает группу , пробегает группу  , то , то

Предположим, что  и и 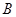 неэквивалентны. Тогда в силу леммы Шура неэквивалентны. Тогда в силу леммы Шура 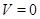 . Отсюда для . Отсюда для 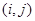 -го элемента матрицы -го элемента матрицы 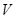 получаем получаем

В частности, если взять  для некоторой пары для некоторой пары 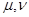 и и  в остальных случаях, то в остальных случаях, то

Пусть теперь 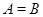 . Тогда в силу теоремы 3.2 . Тогда в силу теоремы 3.2 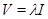 для некоторого для некоторого  . При этом . При этом 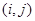 -ый элемент матрицы -ый элемент матрицы  равен равен

где 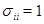 и и 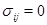 для для  . Вычислив след матрицы . Вычислив след матрицы

мы получаем  (здесь (здесь  – степень представления – степень представления 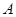 ), откуда ), откуда
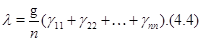
Пусть  для некоторой пары для некоторой пары 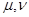 и и 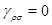 , если , если  или или  . Тогда . Тогда

Тем самым мы получаем следующее утверждение.
Теорема 4.3.
Пусть  – группа порядка
g. – группа порядка
g.
(1) Пусть 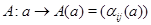 – неприводимое представление группы – неприводимое представление группы  степени степени  . Тогда . Тогда

(2) Пусть  – неприводимое представление, не эквивалентное представлению – неприводимое представление, не эквивалентное представлению  . Тогда . Тогда

Пусть 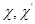 – характеры представлений – характеры представлений  и и 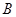 . Положив в предыдущей теореме . Положив в предыдущей теореме  и просуммировав по и просуммировав по  , мы получаем теорему. , мы получаем теорему.
Теорема 4.4.
(Первое соотношение ортогональности для характеров.) Пусть  – группа порядка
g. – группа порядка
g.
(1) Если  – неприводимый характер группы – неприводимый характер группы  , то , то

(2) Если 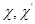 – характеры неэквивалентных неприводимых представлений группы – характеры неэквивалентных неприводимых представлений группы  , то , то

Отметим, что 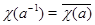 для всех для всех 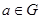 , поскольку теорема 2.3 утверждает, что , поскольку теорема 2.3 утверждает, что  эквивалентно некоторому унитарному представлению эквивалентно некоторому унитарному представлению  и потому и потому

Пусть  – представители классов эквивалентности неприводимых представлений группы – представители классов эквивалентности неприводимых представлений группы  и и  – характеры представлений – характеры представлений  . Обозначим через . Обозначим через  классы сопряженных элементов группы классы сопряженных элементов группы  , причем , причем  , и пусть , и пусть  – представители этих классов. Поскольку характеры – это функции классов, теорема 4.4 может быть переписана в следующем виде. – представители этих классов. Поскольку характеры – это функции классов, теорема 4.4 может быть переписана в следующем виде.
Теорема  .
. 
Для функций  , определенных на группе , определенных на группе 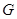 порядка порядка  и принимающих значения в поле и принимающих значения в поле  , определим скалярное произведение , определим скалярное произведение
 по следующему правилу: по следующему правилу:

В случаях, когда ясно, о какой группе идет речь, мы иногда вместо 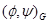 будем писать будем писать  . Очевидно, что скалярное произведение является симметричной билинейной формой: . Очевидно, что скалярное произведение является симметричной билинейной формой:


В этих обозначениях первое соотношение ортогональности для характеров можно сформулировать так:
Теорема 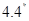 . Пусть
. Пусть  – характеры попарно неэквалентных неприводимых представлений группы – характеры попарно неэквалентных неприводимых представлений группы 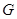 . Тогда . Тогда 
Кратности неприводимых представлений.
Пусть 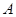 – некоторое представление группы – некоторое представление группы 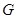 . Поскольку оно вполне приводимо в силу теоремы 2.3, оно эквивалентно представлению . Поскольку оно вполне приводимо в силу теоремы 2.3, оно эквивалентно представлению
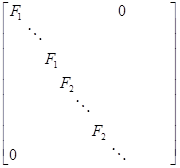
где  – неэквивалентные неприводимые представления. Число – неэквивалентные неприводимые представления. Число  называется кратностью
представления называется кратностью
представления  в в 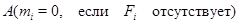 , и мы записываем , и мы записываем

Пусть 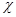 – характер представления – характер представления 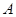 и и  – характер представления – характер представления  . Тогда . Тогда

Если 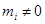 , то , то  и и  называют неприводимыми компонентами
представления называют неприводимыми компонентами
представления 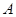 и характера и характера 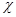 соответственно. соответственно.
Теорема 4.5.
Пусть 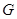 – группа и – группа и 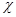 – характер некоторого ее представления. Пусть – характер некоторого ее представления. Пусть  – кратность неприводимого характера – кратность неприводимого характера  в в 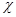 . Тогда . Тогда

Доказательство. Пусть разложение 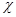 в сумму неприводимых характеров имеет вид в сумму неприводимых характеров имеет вид 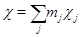 , где , где 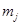 – кратность – кратность  . Тогда . Тогда

Теорема 4.6.
Пусть  – представления группы – представления группы 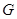 , а , а  – их характеры. Тогда – их характеры. Тогда 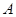 и и  эквивалентны в том и только том случае, когда эквивалентны в том и только том случае, когда  . .
Доказательство. В силу предыдущей теоремы кратности компоненты  в в 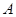 и и  определяются характерами последних. Поскольку каждое представление группы определяются характерами последних. Поскольку каждое представление группы  вполне приводимо, представления вполне приводимо, представления 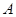 и и  эквивалентны тогда и только тогда, когда каждое неприводимое представление эквивалентны тогда и только тогда, когда каждое неприводимое представление  имеет в имеет в 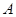 и и  одну ту же кратность. Таким образом, одну ту же кратность. Таким образом, 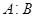 тогда и только тогда, когда тогда и только тогда, когда  . .
Пусть  – характер правого регулярного представления группы – характер правого регулярного представления группы  порядка порядка  . Отметим, что . Отметим, что

Для характера  произвольного неприводимого представления произвольного неприводимого представления  выполняется соотношение выполняется соотношение

 равно степени представления равно степени представления  ). Следовательно, справедлива следующая ). Следовательно, справедлива следующая
Теорема 4.7.
Пусть  – характер правого регулярного представления группы – характер правого регулярного представления группы  . Тогда каждое неприводимое представления . Тогда каждое неприводимое представления  этой группы входит в этой группы входит в 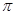 с кратностью с кратностью 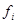 , где , где 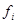 – степень представления – степень представления  . Таким образом, . Таким образом,

где суммирование ведется по всем неприводимым характерам  группы группы  . .
Заметим, что правое и левое регулярные представления эквивалентны, поскольку характер  левого регулярного представления также удовлетворяет равенству (4.8). Поэтому левого регулярного представления также удовлетворяет равенству (4.8). Поэтому  . .
Теорема 4.7 утверждает, что каждый неприводимый характер входит в 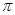 в качестве компоненты, и поэтому в качестве компоненты, и поэтому  имеет лишь конечное число неприводимых характеров. Ниже мы покажем, что число неприводимых характеров группы имеет лишь конечное число неприводимых характеров. Ниже мы покажем, что число неприводимых характеров группы  совпадает с числом ее классов сопряженных элементов. совпадает с числом ее классов сопряженных элементов.
Теорема 4.8.
Пусть 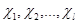 – полный набор различных неприводимых характеров группы – полный набор различных неприводимых характеров группы 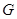 . Пусть . Пусть 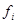 – степень – степень 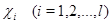 , а , а  – порядок группы – порядок группы  . Тогда . Тогда
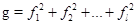
и

для  . .
Для доказательства достаточно вычислить 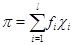 на элементе на элементе  , используя (4.8). , используя (4.8).
Второе соотношение ортогональности для характеров.
Пусть 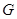 – группа, а – группа, а  – ее классы сопряженных элементов. Образуем формальную сумму элементов из класса – ее классы сопряженных элементов. Образуем формальную сумму элементов из класса  : :

Определим произведение  и и  по правилу по правилу

где 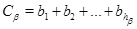 , а суммирование ведется по , а суммирование ведется по  . Для элемента . Для элемента  обозначим через обозначим через 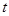 число пар число пар  , таких, что , таких, что  . Тогда для . Тогда для  имеется в точности имеется в точности  пар пар 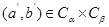 , таких, что , таких, что  , поскольку , поскольку 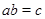 тогда и только тогда, когда тогда и только тогда, когда  для для 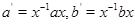 . Поэтому каждый элемент из . Поэтому каждый элемент из  появляется в правой части равенства (4.9) одно и то же число раз, т.е. появляется в правой части равенства (4.9) одно и то же число раз, т.е.
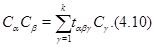
Совокупность всех элементов  для для 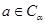 также образует класс сопряженных элементов. Обозначим этот класс через также образует класс сопряженных элементов. Обозначим этот класс через  . .
Тогда

Пусть  – неприводимое представление группы – неприводимое представление группы  и и 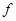 – степень – степень  . Определим . Определим  по правилу по правилу
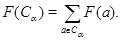
Тогда

поскольку  пробегает пробегает  , как и , как и 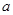 . Значит, . Значит,  коммутируют с коммутируют с  и в силу теоремы 3.2 и в силу теоремы 3.2

Взяв след от обеих частей равенства (4.12), мы получим

где 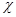 – характер представления – характер представления  и и 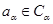 . В силу (4.10) . В силу (4.10)
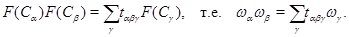
Подставив в это равенство (4.13), мы придем к равенству

или

Пусть 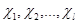 – все различные неприводимые характеры группы – все различные неприводимые характеры группы 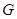 и и  – степень – степень  . Равенство (4.14) имеет место для каждого . Равенство (4.14) имеет место для каждого  . Просуммировав (4.14) по . Просуммировав (4.14) по  , получим , получим
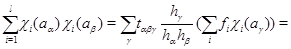


Отсюда
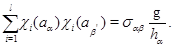
Величина 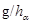 равна порядку централизатора равна порядку централизатора  элемента элемента 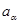 в группе в группе 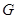 . Поскольку в силу (4.5) . Поскольку в силу (4.5)  , мы получаем следующее утверждение. , мы получаем следующее утверждение.
Теорема 4.9.
(Второе соотношение ортогональности для характеров.) Пусть  – множество всех различных неприводимых характеров группы – множество всех различных неприводимых характеров группы 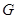 , и пусть , и пусть  – полный набор представителей классов сопряженных элементов группы – полный набор представителей классов сопряженных элементов группы 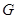 . Тогда . Тогда

где  – порядок – порядок  и суммирование ведется по всем неприводимым характерам и суммирование ведется по всем неприводимым характерам  группы группы 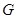 . .
Теорема 4.10.
Число различных неприводимых характеров группы 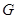 равно числу ее классов сопряженных элементов. равно числу ее классов сопряженных элементов.
Доказательство. Мы воспользуемся следующим простым фактом, касающимся матриц. Пусть 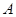 есть есть  – матрица, а – матрица, а  есть есть  – матрица. Если определитель квадратной матрицы – матрица. Если определитель квадратной матрицы 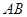 , имеющий порядок , имеющий порядок  , отличен от нуля, то , отличен от нуля, то  . .
Пусть 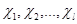 – все различные неприводимые характеры группы – все различные неприводимые характеры группы  , а , а  – полный набор представителей классов сопряженных элементов этой группы. Тогда по теореме – полный набор представителей классов сопряженных элементов этой группы. Тогда по теореме 

Поэтому  . В силу теоремы 4.9 . В силу теоремы 4.9

Отсюда следует, что  и потому и потому  . .
Пусть 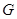 – группа и – группа и 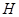 – ее подгруппа. Обозначим через – ее подгруппа. Обозначим через  и и  порядки групп порядки групп  и и  соответственно. Если соответственно. Если 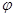 – некоторая функция на – некоторая функция на  , то через , то через 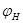 обозначим ее ограничение на обозначим ее ограничение на  . В случае когда . В случае когда  – функция классов на – функция классов на 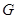 , ,  также является функцией классов на также является функцией классов на 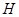 . Если . Если  – характер некоторого представления – характер некоторого представления 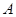 группы группы  , то , то  представляет собой характер ограничения представляет собой характер ограничения 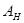 представления представления 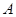 на на  . .
По функции  , заданной на , заданной на  , определим функцию , определим функцию  на на  правилом правилом

полагая  для для  , не принадлежащих , не принадлежащих  . Отметим, что . Отметим, что  является функцией классов на является функцией классов на  , даже еслм , даже еслм  не является функцией классов на не является функцией классов на  . Если . Если 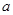 не сопряжен ни с каким элементом из не сопряжен ни с каким элементом из  , то , то 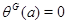 . .
Лемма 5.1.
Пусть 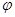 – функция классов на группе – функция классов на группе  , а , а  – функция классов на подгруппе – функция классов на подгруппе  группы группы 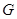 . Тогда . Тогда

Доказательство. Имеем

Вклад в сумму дают лишь такие пары  , что , что 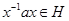 . Поэтому, суммируя по тем парам . Поэтому, суммируя по тем парам  , для которых , для которых 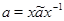 при некотором при некотором  , получаем , получаем

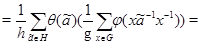

Если  – характер некоторого представления группы – характер некоторого представления группы  , то назовем , то назовем  индуцированным характером
группы индуцированным характером
группы 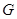 и скажем, что и скажем, что  индуцирован с индуцирован с  . Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы . Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы  . .
Пусть  – множество представителей левых смежных классов группы – множество представителей левых смежных классов группы  по по  : :

Для представления  подгруппы подгруппы  определим матрицу определим матрицу  так: так:

где для  , не содержащихся в , не содержащихся в 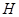 , полагаем , полагаем  . Это обобщение правого регулярного представления группы . Это обобщение правого регулярного представления группы 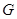 . Мы покажем, что . Мы покажем, что

– представление группы  степени степени  , где , где 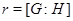 , а , а 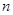 – степень – степень 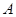 . При фиксированных . При фиксированных 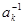 и и 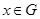 множество множество  содержит по одному представителю из каждого левого смежного класса по содержит по одному представителю из каждого левого смежного класса по  , поэтому среди матриц , поэтому среди матриц  , лишь одна ненулевая. Аналогично, множество , лишь одна ненулевая. Аналогично, множество  содержит по одному представителю из каждого правого смежного класса по содержит по одному представителю из каждого правого смежного класса по 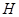 и среди матриц и среди матриц 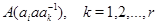 , также лишь одна ненулевая. Обозначим , также лишь одна ненулевая. Обозначим  -й блок матрицы -й блок матрицы  через через  . Тогда . Тогда

Покажем, что  . Имеется единственное число . Имеется единственное число  , такое, что , такое, что  , и единственное число , и единственное число  , такое, что , такое, что 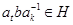 . Если . Если  , то , то  . Если же . Если же  , то , то  и и  , поскольку , поскольку 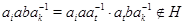 . В любом случае . В любом случае  и следовательно, и следовательно,  . Поскольку . Поскольку  , матрица , матрица  невырожденна. Таким образом невырожденна. Таким образом  является представлением группы является представлением группы  . .
Пусть  – характер – характер 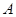 , а , а 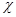 – характер – характер  . Тогда . Тогда


Тем самым мы получим  . Назовем . Назовем  индуцированным представлением
группы индуцированным представлением
группы 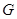 и будем говорить, что и будем говорить, что 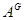 индуцировано с индуцировано с 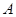 . Сказанное суммирует следующая . Сказанное суммирует следующая
Теорема 5.2.
Пусть  – группа и – группа и 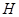 – ее подгруппа. Пусть – ее подгруппа. Пусть 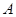 – представление – представление 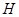 степени степени  , а , а  – его характер. Тогда индуцированное представление – его характер. Тогда индуцированное представление  имеет степень имеет степень  , где , где  , и характер , и характер

Теорема 5.3.
(Закон взаимности Фробениуса.) Пусть  – подгруппа в – подгруппа в  . Пусть . Пусть  – полный набор неприводимых характеров группы – полный набор неприводимых характеров группы 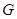 , а , а  – полный набор неприводимых характеров группы – полный набор неприводимых характеров группы 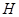 . Тогда . Тогда

в том и только том случае, когда

Другими словами, если 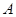 – неприводимое представление группы – неприводимое представление группы  , а , а  – неприводимое представление – неприводимое представление 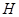 , то , то  является неприводимой компонентой в является неприводимой компонентой в 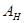 кратности кратности 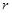 тогда и только тогда, когда тогда и только тогда, когда 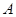 является неприводимой компонентой в является неприводимой компонентой в  кратности кратности  . .
Доказательство. Пусть  и и 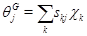 . В силу леммы 5.1 . В силу леммы 5.1

Пусть  – квадратные матрицы порядков – квадратные матрицы порядков  и и  соответственно, и пусть соответственно, и пусть  . Определим кронекерово
, или тензорное
, произведение . Определим кронекерово
, или тензорное
, произведение 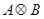 матриц матриц 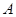 и и  следующим образом: следующим образом:

Значит,  представляет собой квадратную матрицу порядка представляет собой квадратную матрицу порядка  . Непосредственными вычислениями устанавливается следующая . Непосредственными вычислениями устанавливается следующая
Лемма 6.1.
(1)  , ,
(2) если 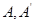 имеют степень имеют степень  , a , a  – степень – степень  , то , то 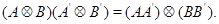
Пусть  и и 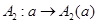 – представления группы – представления группы  . Тогда в силу леммы 6.1 (2) отображение . Тогда в силу леммы 6.1 (2) отображение

также является представлением этой группы. Такое представление называют произведением
представлений  и обозначают через и обозначают через  . Пусть . Пусть  – характеры представлений – характеры представлений 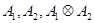 соответственно. По лемме 6.1 (1) соответственно. По лемме 6.1 (1)
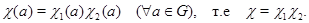
Пусть  – полный набор неприводимых представлений группы – полный набор неприводимых представлений группы 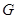 , а , а  – характер – характер  . Отображение . Отображение  также является неприводимым, и его характер – это также является неприводимым, и его характер – это  , где , где  . Пусть . Пусть  . .
Теорема 6.2.
Равенство
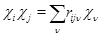
имеет место тогда и только тогда, когда

Доказательство.
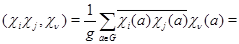

Таким образом, кратность вхождения  в в  равна кратности вхождения равна кратности вхождения  в в 
Теорема 6.3.
Пусть 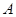 – точное представление группы – точное представление группы  и и  – его характер. Пусть – его характер. Пусть  – число различных значений, которые принимает – число различных значений, которые принимает  на на  . Тогда каждое неприводимое представление группы . Тогда каждое неприводимое представление группы 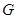 входит в входит в

для некоторого 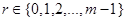 , где , где  . .
Доказательство. Предположим, что неприводимое представление  не входит в не входит в  . Пусть . Пусть  – характеры – характеры 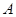 и и  соответственно. Тогда соответственно. Тогда

для  . Пусть . Пусть 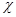 принимает на принимает на 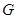 значение значение  . Положим . Положим 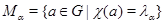 и и  . В силу (6.1) . В силу (6.1)
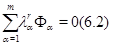
для  Рассмотрим (6.2) как систему линейных уравнений для Рассмотрим (6.2) как систему линейных уравнений для 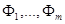 . Поскольку . Поскольку 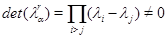 , эта система имеет решение , эта система имеет решение  . .
Пусть 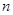 – степень представления – степень представления 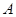 , т.е. , т.е.  . Мы можем считать, что . Мы можем считать, что  . Покажем, что . Покажем, что  . Пусть . Пусть  , т.е. , т.е.  . Обозначим через . Обозначим через  циклическую группу, порожденную элементом циклическую группу, порожденную элементом 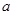 . По теореме 3.3 . По теореме 3.3  эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы 

Пусть  – порядок элемента – порядок элемента  . Тогда . Тогда 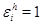 . Взяв след в равенстве (6.3), получаем . Взяв след в равенстве (6.3), получаем  . Это означает, что . Это означает, что  , т.е. , т.е.  . Плскольку . Плскольку 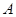 точно, точно,  . Поэтому . Поэтому  и и  . Полученное противоречие доказывает теорему. . Полученное противоречие доказывает теорему. 
Таблицы характеров.
Пусть  – группа и – группа и  – классы сопряженных элементов в – классы сопряженных элементов в  . Пусть . Пусть 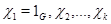 – нерпиводимые характеры группы – нерпиводимые характеры группы 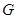 , а , а 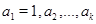 – представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения – представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения  таким образом, чтобы получить таблицу характеров
группы таким образом, чтобы получить таблицу характеров
группы 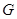 , в которой строки помечены различными неприводимыми характерами, начиная с , в которой строки помечены различными неприводимыми характерами, начиная с 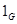 , а столбцы – классами сопряженности группы , а столбцы – классами сопряженности группы 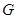 , начиная с класса , начиная с класса  . .
Различные строки таблицы характеров ортогональны между собой в смысле теоремы  , а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства. , а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
Заключение
Таким образом, в данной работе мы показали, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.
Путем прямых вычислений доказали лемму:
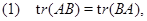
 для произвольной квадратной матрицы для произвольной квадратной матрицы  и теорему: Пусть
и теорему: Пусть 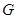 – группа и – группа и 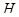 – ее подгруппа. Пусть – ее подгруппа. Пусть 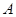 – представление – представление  степени степени  , а , а  – его характер. Тогда индуцированное представление – его характер. Тогда индуцированное представление  имеет степень имеет степень 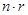 , где , где  , и характер , и характер

Непосредственными вычислениями была устанавлена следующая лемма:  , ,
(2) если  имеют степень имеют степень 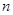 , a , a 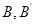 – степень – степень 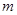 , то , то 
Список использованных источников
Сыскин С.А. Абстрактные свойства простых спорадических групп. – Усп. мат. наук, 1980, т. 35, №5, (215), с. 181–212.
Монахов В.С. О трижды факторизуемых группах. – Изв. АН БССР. Сер. физ.-мат. наук, 1981, №6, с. 18–23.
Монахов В.С. Произведение разрешимой и циклической групп // Сб. VI всес. симпозиум по теории групп.-Киев: Наукова думка, 1980-с. 189–195
Монахов В.С. О произведении двух групп с циклическими подгруппами индекса 2 // Весцi АН Беларусi. сер. фiз.-мат. навук. – 1996, №3-с. 21–24
|