Контрольная работа: Чисельне розвязання задач оптимального керування
|
Название: Чисельне розвязання задач оптимального керування Раздел: Рефераты по информатике Тип: контрольная работа |
ЧИСЕЛЬНЕ РОЗВ’ЯЗАННЯ ЗАДАЧ оптимального керування1 Дискретизація задачі із закріпленим лівим і вільним правим кінцем. Необхідні умови оптимальностіРозглянемо неперервну задачу оптимального керування
Виконаємо дискретну апроксимацію даної задачі. Для цього розіб’ємо відрізок
Тепер дискретна задача оптимального керування, що апроксимує неперервну задачу (1) – (3), матиме вигляд:
Для пошуку оптимального розв’язку отриманої дискретної задачі може бути застосований метод множників Лагранжа. Функція Лагранжа має вигляд:
де Обмеження на керування введемо далі, під час реалізації чисельного методу. Відзначимо, що перед першим доданком стоїть знак «–», оскільки Якщо 1.
2.
Із (9) одержимо ітераційні співвідношення для спряжених змінних
Перепишемо співвідношення (12) у вигляді:
Очевидно, що останнє співвідношення є аналогом спряженої системи для неперервних задач керування. Дійсно,
Якщо
Зі співвідношення (13) випливає, що Сформулюємо критерій оптимальності для задачі (4) – (7). Вважатимемо, що функції 1) умови стаціонарності в точці
2) Розпишемо (14), використовуючи вираз для функції Лагранжа:
Перетворимо вираз під знаком мінімуму, переходячи до довільного
Або
Якщо
2 Ітераційний метод розв’язання дискретної задачі оптимального керування з двійним перерахуваннямРозглянемо ітераційний метод пошуку оптимального керування задачі (4) – (7). Суть методу полягає в тому, що на кожній ітерації обчислюються два вектори: Контроль у методі подвійного перерахування полягає в повторному перерахуванні результатів задачі і порівнянні отриманих даних для різних значень кроку розбиття. У випадку розбіжності виконується корекція і обчислення повторюються. Розглянемо алгоритм методу. 1. Задаємо крок розбиття 2. Задаємо початкове наближення – припустимий набір керувань на кожному кроці – початкову стратегію керування:
де 3. За визначеною в п. 2 стратегією керування
на початкової ітерації
4. Визначаємо початкове наближення 5. Знаходимо спряжені змінні за формулами (12) – (13). Визначаємо наступні наближення до оптимального керування
в момент
7. Обчислюємо відповідну стратегії
за формулами (4), (6):
8. Знаходимо наступне наближення цільового функціонала
9. Якщо
10. Перевіряємо, чи виконується задана точність обчислень. Якщо
то переходимо до п. 13, інакше – до п. 11. 11. Позначаємо
12. Виконуємо наступний крок ітераційного методу – п. 5. 13. Позначаємо
1 Якщо крок 15. Ділимо крок
1 Перевіряємо задану точність. Якщо
то переходимо до п. 18, інакше переходимо до п. 17. 17. Позначаємо
18. Кінець алгоритму. 3. Оптимальне стохастичне керування: формулювання із зовнішнім інтеграломРозглянемо відображення
за таких припущень: параметр
функції скаляр Формули (1), (6) є окремими випадками відображення Очевидно, що відображення Для початкового стану
у сукупності із системою рівнянь
визначають єдину міру
то функція витрат за де стани Рекурентне співвідношення методу динамічного програмування для розв’язання багатоетапних задач оптимального стохастичного керування зі скінченним горизонтом можна записати так:
де 4 Оптимальне стохастичне керування:мультиплікативний функціонал витратРозглянемо відображення
за припущення, що параметр Якщо
а відповідна задача з нескінченним горизонтом:
Границя в (23) існує, якщо Самостійний інтерес становить задача з експоненціальною функцією витрат
де Для розв’язання багатоетапних задач оптимального стохастичного керування з мультиплікативним функціоналом витрат використовується таке рекурентне співвідношення алгоритму динамічного програмування:
де 5. Мінімаксне керуванняРозглянемо задачу керування системою, у якій некерованими впливами є стратегії супротивника (або явища природи)
за таких припущень: параметр функції скаляр За таких умов припущення про монотонність для відображення
Задача з нескінченним горизонтом формулюється аналогічно:
Границя у співвідношенні (25) існує при виконанні будь-якої з умов: · · · Для розв’язання багатокрокових мінімаксних задач оптимального стохастичного керування рекурентне співвідношення алгоритму динамічного програмування використовується у такому вигляді:
|
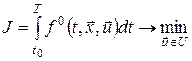 ,(2)
,(2)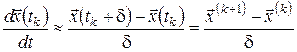 .
.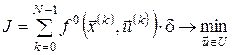 , (5)
, (5) 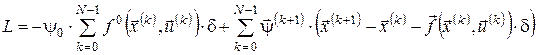 ,
, 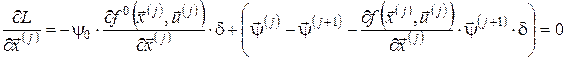 ,
,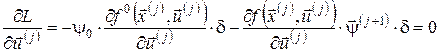 ,
,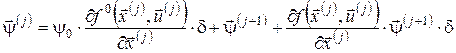
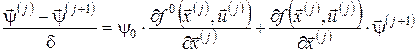 .
.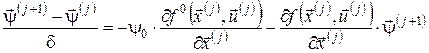 .
.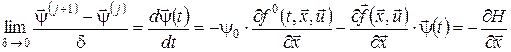 .
.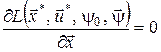 ;
;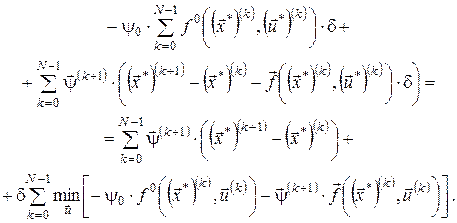
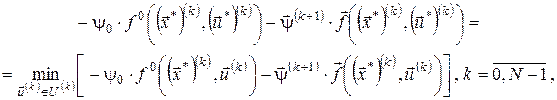
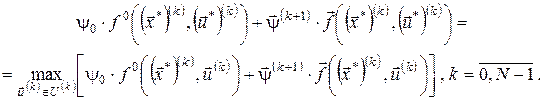
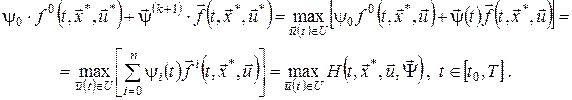
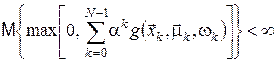 або
або 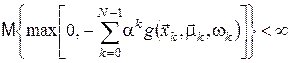 ,
,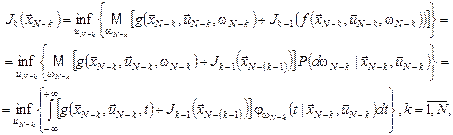
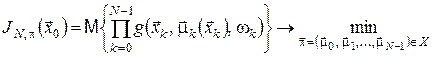 , (20)
, (20)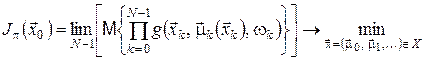 , (22)
, (22)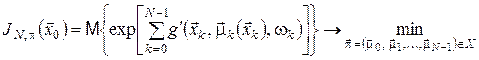 ,
,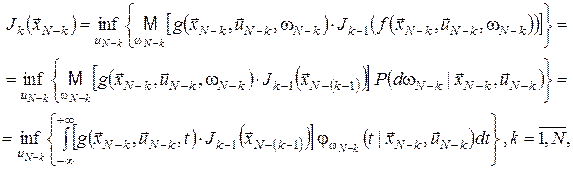
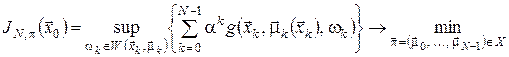 , (17)
, (17)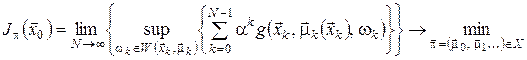 , (24)
, (24)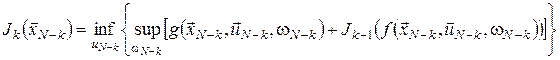 ,
,