Содержание
Введение 3
Цель работы 4
Решение
IФинансовые функции 5
IIОптимизационные задачи 12
Заключение 33
Введение
Успех в современном бизнесе и менеджменте во многом опирается на оперативный анализ экономической ситуации и выбор оптимального решения из возможных альтернатив. Одним из современных компьютерных средств для решения подобных задач является программа MicrosoftExcel.
Первые формальные разработки по исследованию операций были инициированы в Англии во время Второй мировой войны, когда команда британских ученых сформулировала и нашла решение задачи наиболее эффективной доставки военного снаряжения на фронт. После окончания войны эти идеи были перенесены в гражданскую сферу для повышения эффективности и продуктивности экономической и производственной деятельности. Сегодня теория исследования операций является основным и неотъемлемым инструментом при принятии решений в самых разнообразных областях человеческой деятельности.
Краеугольным камнем исследования операций является математическое моделирование. Хотя данные, полученные в процессе исследования математических моделей, являются основой для принятия решений, окончательный выбор обычно делается с учетом многих других "нематериальных" (не имеющих числового выражения) факторов (таких как человеческое поведение), которые невозможно отобразить в математических моделях.
Цель работы
На сегодняшний момент существуют разнообразные программные продукты, с помощью которых рядовой пользователь очень быстро решает прикладные задачи. На решение таких задач в сфере экономики, финансов и статистики у программистов прежних поколений уходили месяцы. Одной из программ, завоевавших репутацию надежного инструмента для повседневного аналитического труда, является процессор электронных таблиц MicrosoftExcel. Целью данной работы является решение финансово-экономических и оптимизационных задач линейного программирования при помощи MicrosoftExcel.
Решение
I
Финансовые функции.
Функция ПЛТ вычисляет величину постоянной периодической ренты (например, регулярных платежей по займу) при постоянной процентной ставке.
Синтаксис:
ПЛТ
(ставка
; кпер
; пс
; бс; тип)
Ставка
– процентная ставка по ссуде.
Кпер
– общее число выплат по ссуде.
Пс
– приведенная к текущему моменту стоимость, или общая сумма, которая на текущий момент равноценна ряду будущих платежей, называемая также основной суммой.
Бс
– требуемое значение будущей стоимости, или остатка средств после последней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, например, значение бс равно 0.
Тип
– число 0 (нуль) или 1, обозначающее, когда должна производиться выплата.
Очень важно быть последовательным в выборе единиц измерения для задания аргументов Ставка
и Кпер
. Например, если производятся ежемесячные выплаты по четырехгодичному займу из расчета 12% годовых, то для задания аргумента ставка используется 12%/12, а для задании аргумента Кпер
– 4*12. Если производятся ежегодные платежи по тому же займу, то для задания аргумента ставка используется 12%, а для задания аргумента Кпер
– 4.
Для нахождения обшей суммы, выплачиваемой на протяжении интервала выплат, необходимо умножить возвращаемое функцией ПЛТ
значение на величину Кпер
. Интервал выплат – это последовательность постоянных денежных платежей, осуществляемых за непрерывный период. Например, заем под автомобиль или заклад являются интервалами выплат. В функциях, связанных с интервалами выплат, выплачиваемые вами деньги, такие как депозит на накопление, представляются отрицательным числом, а деньги, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом. Например, депозит в банк на сумму 1000 руб. представляется аргументом -1000, если вы вкладчик, и аргументом 1000, если вы – представитель банка.
Задача № 1
(Вариант 2 Задача № 1)
Для приведенного на рис 1.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 1.2.

Рисунок 1.1

Рисунок 1.2
Задача № 2
(Вариант 2 Задача № 2)
Функция ПС
возвращает приведенную (к текущему моменту) стоимость инвестиции. Приведенная (нынешняя) стоимость представляет собой общую сумму, которая на настоящий момент равноценна ряду будущих выплат. Например, когда вы занимаете деньги, сумма займа является приведенной (нынешней) стоимостью для заимодавца. Синтаксис ПС
(ставка
; кпер
; плт
; бс; тип)
Для приведенного на рис 2.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 2.2.

Рисунок 2.1

Рисунок 2.2
Задача № 3
(Вариант 2 Задача № 3)
ЧПС
Возвращает величину чистой приведенной стоимости инвестиции, используя ставку дисконтирования, а также стоимости будущих выплат (отрицательные значения) и поступлений (положительные значения).
Синтаксис
ЧПС
(ставка
; значение1
; значение2; …)
Ставка
– ставка дисконтирования за один период.
Значение1, значение2
,… – от 1 до 29 аргументов, представляющих расходы и доходы.
- Значение1, значение2
, … должны быть равномерно распределены во времени, выплаты должны осуществляться в конце каждого периода.
- ЧПС
использует порядок аргументов значение1, значение2
, … для определения порядка поступлений и платежей. Необходимо, чтобы платежи и поступления введены в правильном порядке.
- Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел, учитываются; аргументы, которые являются значениями ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются.
- Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, текст или значения ошибок в массиве или ссылке игнорируются.
- Считается, что инвестиция, значение которой вычисляет функция ЧПС
, начинается за один период до даты денежного взноса значение1 и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС
базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС
, но не включать в список аргументов.
- ЧПС
аналогична функции ПС
(текущее значение). Основное различие между функциями ПС
и ЧПС
заключается в том, что ПС
допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции ЧПС
, денежные взносы в функции ПС
должны быть постоянны на весь период инвестиции.
Для приведенного на рис 3.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 3.2.

Рисунок 3.1

Рисунок 3.2
Задача № 4
(Вариант 2 Задача № 4)
Для приведенного на рис 4.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 4.2.

Рисунок 4.1

Рисунок 4.2
Задача № 5
(Вариант 2 Задача № 5)
Для приведенного на рис 5.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 5.2.

Рисунок 5.1

Рисунок 5.2
Из результатов расчета видно, что для фирмы предпочтительнее приобрести облигацию.
II
Решение оптимизационных задач линейного программирования
Линейное программирование (ЛП) – это метод оптимизации моделей, в которых целевые функции и ограничения строго линейны. ЛП успешно применяется в военной области, индустрии, сельском хозяйстве, транспортной отрасли, экономике, системе здравоохранения и даже в социальных науках. Широкое использование этого метода также подкрепляется высокоэффективными компьютерными алгоритмами, реализующими данный метод. На алгоритмах линейного программирования (учитывая их компьютерную эффективность) базируются оптимизационные алгоритмы для других, более сложных типов моделей и задач исследования операций, включая целочисленное, нелинейное и стохастическое программирование.
Задача (модель) ЛП, как и любая задача исследования операций, включает три основных элемента.
1. Переменные,
которые следует определить.
2. Целевая функция,
подлежащая оптимизации.
3. Ограничения,
которым должны удовлетворять переменные.
Определение переменных – первый шаг в создании модели. После определения переменных построение ограничений и целевой функции обычно не вызывает трудностей.
Задача № 6
(Вариант 6 Задача № 1)
В данной задаче необходимо спланировать объем производства так, чтобы максимизировать прибыль. Обозначим через  , ,  , ,  – объемы производства трельяжа, трюмо и тумбочки под телевизор соответственно. Суммарная прибыль от производства равна: – объемы производства трельяжа, трюмо и тумбочки под телевизор соответственно. Суммарная прибыль от производства равна:
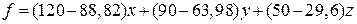 . .
Целью комбината является определение среди всех допустимых значений  , ,  , ,  таких, которые максимизируют суммарную прибыль, т. е. целевую функцию таких, которые максимизируют суммарную прибыль, т. е. целевую функцию 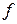 .
Перейдем к ограничениям, которые налагаются на .
Перейдем к ограничениям, которые налагаются на  , ,  , ,  .
Объем производства мебели не может быть отрицательным, следовательно: .
Объем производства мебели не может быть отрицательным, следовательно:
 . .
Расход древесно-стружечных плит для производства всех видов мебели не может превосходить максимально возможный запас, следовательно:
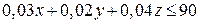 , ,
 , ,
 . .
Кроме того, общая трудоемкость для производства всех видов мебели не должна превосходить плановый фонд рабочего времени, следовательно:

Таким образом, математическая модель данной задачи имеет следующий вид:
максимизировать
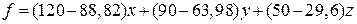
при следующих ограничениях:

Данная модель является линейной, т. к. целевая функция и ограничения линейно зависят от переменных.
Задача решается в MicrosoftExcelпри помощи команды Сервис
, Поиск решения
. Ячейки А11, В11, С11 отведены под значения переменных  , ,  , ,  .
В ячейку Е10 введена целевая функция. .
В ячейку Е10 введена целевая функция.
Для приведенного на рис 6.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 6.2.

Рисунок 6.1

Рисунок 6.2
В диалоговом окне Поиск решения
введены данные, показанные на рис 6.3 и рис 6.4.

Рисунок 6.3

Рисунок 6.4
В поле Установить целевую ячейку
диалогового окна Поиск решения
дается ссылка на ячейку с функцией, для которой будет находиться максимум, минимум или заданное значение. Для данной задачи в поле Установить целевую ячейку
вводится $Е$10 (рис. 6.3).
Тип взаимосвязи между решением и целевой ячейкой задается путем установки переключателя в группе Равной
. Для нахождения максимального или минимального значения целевой функции этот переключатель ставится в положение максимальному значению
или минимальному значению
, соответственно. Для нахождения значения целевой функции, заданного в поле группы Равной
, переключатель ставится в положение значению
. В данной задаче переключатель установлен в положение максимальному значению
, т. к. планируем производство, обеспечивающее максимальную прибыль.
В поле Изменяя ячейки
указываются ячейки, которые должны изменяться в процессе поиска решения задачи, т. е. ячейки отведенные под переменные задачи. В нашем случае введем в поле Изменяя ячейки
диапазон $А$11:$С$11.
Ограничения, налагаемые на переменные задачи, отображаются в поле Ограничения
(рис. 6.3). Средство поиска решений допускает ограничения в виде равенств, неравенств, а также позволяет ввести требование целочисленности переменных. Ограничения добавляются по одному. Для ввода ограничений необходимо нажать кнопку Добавить
(Add) в диалоговом окне Поиск решения
(рис. 6.3) и в открывшемся диалоговом окне Добавление ограничения
(рис. 6.5) заполнить поля.

Рисунок 6.5
В поле Ссылка на ячейку
вводится левая часть ограничения – $D$13, а в поле Ограничение –
правая часть, в данной задаче – ячейка $В$7. С помощью раскрывающегося списка вводится тип соотношения между левой и правой частями ограничения. В данной задаче это <=.
После ввода всех ограничений необходимо нажать кнопку Параметры
в диалоговом окне Поиск решения
(рис. 6.3), для того чтобы проверить, какие параметры заданы для поиска решений.
В открывшемся диалоговом окне Параметры поиска решения
(рис. 6.2) можно изменять условия и варианты поиска решения исследуемой задачи, а также загружать и сохранять оптимизируемые модели. Значения и состояния элементов управления, используемые по умолчанию, подходят для решения большинства задач.
Рассмотрим элементы этого окна:
- Поле Максимальное время
служит для ограничения времени, отпускаемого на поиск решения задачи;
- Поле Предельное число итераций
служит для ограничения числа промежуточных вычислений;
- Поля Относительная погрешность
и Допустимое отклонение
служат для задания точности, с которой ищется решение. Рекомендуется после нахождения решения с величинами данных параметров, заданными по умолчанию, повторить вычисления с большей точностью и меньшим допустимым отклонением и сравнить с первоначальным решением. Использование подобной проверки особенно рекомендуется для задач с требованием целочисленности переменных;
- Флажок Линейная модель
служит для поиска решения линейной задачи оптимизации или линейной аппроксимации нелинейной задачи. В случае нелинейной задачи этот флажок должен быть сброшен, в случае линейной задачи – установлен, т. к. в противном случае возможно получение неверного результата;
- Флажок Показывать результаты итераций
служит для приостановки поиска решения и просмотра результатов отдельных итераций;
- Флажок Автоматическое масштабирование
служит для включения автоматической нормализации входных и выходных значений, качественно различающихся по величине, например, при максимизации прибыли в процентах по отношению к вложениям, исчисляемым в миллионах рублей;
- Группа Оценки
служит для выбора метода экстраполяции;
- Группа Метод
служит для выбора алгоритма оптимизации.
Из результатов расчета видно (см. рис 6.1), что оптимальным является производство 551 трельяжа, 181 трюмо, 1693 тумбочек под телевизор. Этот объем производства принесет мебельному комбинату 56435 у.е. прибыли.
Задача № 7
(Вариант 7 Задача № 1)
В данной задаче необходимо спланировать объем производства так, чтобы максимизировать прибыль. Обозначим через  , ,  , ,  – объемы производства продукции А, В и С соответственно. Суммарная прибыль от производства равна: – объемы производства продукции А, В и С соответственно. Суммарная прибыль от производства равна:
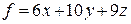 . .
Целью предприятия является определение среди всех допустимых значений  , ,  , ,  таких, которые максимизируют суммарную прибыль, т. е. целевую функцию таких, которые максимизируют суммарную прибыль, т. е. целевую функцию 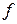 .
Перейдем к ограничениям, которые налагаются на .
Перейдем к ограничениям, которые налагаются на  , ,  , ,  .
Объем производства не может быть отрицательным, следовательно: .
Объем производства не может быть отрицательным, следовательно:
 . .
Расход ресурсов для производства всех видов продукции не может превосходить максимально возможный запас, следовательно:
 , ,
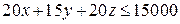 , ,
 , ,
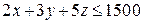 . .
Таким образом, математическая модель данной задачи имеет следующий вид:
максимизировать
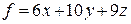
при следующих ограничениях:

Данная модель является линейной, т. к. целевая функция и ограничения линейно зависят от переменных.
Задача решается в MicrosoftExcelпри помощи команды Сервис
, Поиск решения
. Ячейки В13, С13, D13 отведены под значения переменных  , ,  , ,  .
В ячейку F12 введена целевая функция (рис 7.2). .
В ячейку F12 введена целевая функция (рис 7.2).
Для приведенного на рис 7.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 7.2.

Рисунок 7.1

Рисунок 7.2
В диалоговом окне Поиск решения
введены данные, показанные на рис 7.3 и рис 7.4.

Рисунок 7.3

Рисунок 7.4
Из результатов расчета видно (см. рис 7.1), что оптимальным является производство 571 шт. продукции А, 0 шт. продукции В, 71 шт. продукции С. Этот объем производства принесет 4071 у.е. прибыли.
Задача № 8
(Вариант 7 Задача № 2)
Поскольку данная модель сбалансирована (суммарный объем произведенной продукции равен суммарному объему потребностей в ней), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками продукции (см. рис. 8.1).
Для решения данной задачи построим ее математическую модель. Неизвестными в данной задаче являются объемы перевозок, после сокращения. Пусть 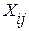 – объем перевозок с – объем перевозок с 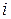 -го кирпичного завода на -го кирпичного завода на  -й строительный объект. Целевая функция – это суммарные расходы на производство и транспортировку кирпича после сокращения, т. е. -й строительный объект. Целевая функция – это суммарные расходы на производство и транспортировку кирпича после сокращения, т. е.
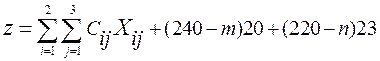
где  – стоимость перевозки одной тонны кирпича с
– стоимость перевозки одной тонны кирпича с 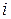 -го кирпичного заводана -го кирпичного заводана  -й строительный объект; -й строительный объект;
 – сокращение объема производства на 1-ом кирпичном заводе; – сокращение объема производства на 1-ом кирпичном заводе;
 – сокращение объема производства на 2-ом кирпичном заводе. – сокращение объема производства на 2-ом кирпичном заводе.
Неизвестные в данной задаче должны удовлетворять следующим ограничениям:
- Объемы перевозок и сокращения не могут быть отрицательными;
- Так как модель сбалансирована, то вся продукция должна быть вывезена с заводов, а потребности всех строительных объектов должны быть полностью удовлетворены.
В результате имеем следующую математическую модель:
минимизировать:

при ограничениях:
 ; ;
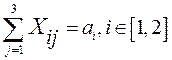 ; ;
 ; ;
 ; ;
где  – объем производства на – объем производства на  -м кирпичном заводе; -м кирпичном заводе;
 – потребность на – потребность на  -м строительном объекте. -м строительном объекте.
Для решения этой задачи с помощью средства поиска решений введем данные, как показано на рис. 8.1.

Рисунок 8.1
В ячейки С5:Е6 введены стоимости перевозок. Ячейки С10:Е11 и I10:I11 отведены под значения неизвестных – объема перевозок и необходимого сокращения объема производства на предприятиях соответственно. В ячейки G10:G11 введены объемыпроизводства на кирпичных заводах, а в ячейки С11:Е13 введена потребность в продукции на строительных объектах (с учетом сокращения объема производства). В ячейку F15 введена целевая функция
=СУММПРОИЗВ(C5:E6;C10:E11)+H5*G10+H6*G11
В ячейки С12:Е12 введены формулы (см. рис. 8.1), определяющие объем продукции, необходимой соответствующему потребителю.
В ячейки F10:F11 введены формулы (см. рис. 8.1), определяющие объем продукции, вывозимой с кирпичных заводов.
Далее выбираем команду Сервис, Поиск решения
и заполняем открывшееся диалоговое окно Поиск решения
, как показано на рис. 8.2.

Рисунок 8.2
В диалоговом окне Параметры поиска решения
(рис. 8.3) устанавливаем флажок Линейная модель
и Неотрицательные значения
. После

Рисунок 8.3
нажатия кнопки Выполнить
средство поиска решений находит оптимальный план поставок продукции и показывает на каких предприятиях необходимо провести сокращение производства (рис 8.4). Т. е. необходимо сократить производство на 140 т на 2-м кирпичном заводе.

Рисунок 8.4
Задача № 9
(Задача № 2-17)
Поскольку данная модель сбалансирована (суммарный объем запасов сырья равен суммарному объему необходимого сырья), то в этой модели не надо учитывать издержки, связанные как со складированием, так и с недопоставками сырья.
Для решения данной задачи построим ее математическую модель. Неизвестными в данной задаче являются объемы перевозок. Пусть 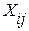 – объем перевозок с – объем перевозок с  -го пункта получения сырья на -го пункта получения сырья на  -е предприятие. Целевая функция – это суммарные транспортные расходы, т. е. -е предприятие. Целевая функция – это суммарные транспортные расходы, т. е.

где 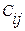 – элемент матрицы С, задающей тарифы перевозок;
– элемент матрицы С, задающей тарифы перевозок;
Неизвестные в данной задаче должны удовлетворять следующим ограничениям:
- Объемы перевозок не могут быть отрицательными;
- Так как модель сбалансирована, то вся продукция должна быть вывезена с мест получения сырья, а потребности всех предприятий должны быть полностью удовлетворены.
В результате имеем следующую математическую модель:
минимизировать:

при ограничениях:
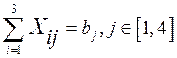 ; ;
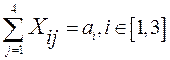 ; ;
 ; ;
где  – запас сырья на – запас сырья на  -м пункте его получения; -м пункте его получения;
 – потребность в сырье на – потребность в сырье на  -м предприятии. -м предприятии.
Для решения этой задачи с помощью средства поиска решений введем данные, как показано на рис. 9.1.

Рисунок 9.1
В ячейки С5:F7 введена матрица С (тарифы перевозок). Ячейки С14:F16 отведены под значения неизвестных – объема перевозок. В ячейку G19 введена целевая функция
.=СУММПРОИЗВ(C5:F7;C14:F16)
В ячейки С17:F17 введены формулы (см. рис. 8.1), определяющие объем сырья, необходимого соответствующему предприятию.
В ячейки G14:G16 введены формулы (см. рис. 8.1), определяющие объем сырья, сосредоточенного на пунктах его получения.
Далее выбираем команду Сервис, Поиск решения
и заполняем открывшееся диалоговое окно Поиск решения
, как показано на рис. 9.2.

Рисунок 9.2
В диалоговом окне Параметры поиска решения
(рис. 9.3) устанавливаем флажок Линейная модель
и Неотрицательные значения
. После

Рисунок 9.3
нажатия кнопки Выполнить
средство поиска решений находит оптимальный план перевозок, при котором общая стоимость перевозок является минимальной (рис 9.4).

Рисунок 9.4
Задача № 10
(Набор задач № 9.1)
В данной задаче необходимо определить суммы кредитов по указанным видам так, чтобы максимизировать доход. Обозначим через  , ,  , ,  , ,  , ,  – суммы кредитов на личные нужды, покупку авто, жилье, с/х и бизнес соответственно. Суммарный доход от размещения всех кредитов, учитывая долю дохода и долю невозврата по каждому из вышеперечисленных кредитов, равен: – суммы кредитов на личные нужды, покупку авто, жилье, с/х и бизнес соответственно. Суммарный доход от размещения всех кредитов, учитывая долю дохода и долю невозврата по каждому из вышеперечисленных кредитов, равен:

Упрощая данное выражение, получим:

Целью банка является определение среди всех допустимых значений  , ,  , ,  , ,  , ,  таких, которые максимизируют суммарный доход, т. е. целевую функцию таких, которые максимизируют суммарный доход, т. е. целевую функцию 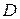 .
Перейдем к ограничениям, которые налагаются на
.
Перейдем к ограничениям, которые налагаются на  , ,  , ,  , ,  , ,  .
Сумма кредита не может быть отрицательным, следовательно: .
Сумма кредита не может быть отрицательным, следовательно:
 . .
Сумма всех кредитов не должна превышать 12 млн $, следовательно:
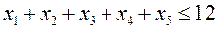
Банк обязан разместить 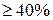 всех кредитов на нужды с/х и бизнеса, следовательно: всех кредитов на нужды с/х и бизнеса, следовательно:
 , упрощая, получим: , упрощая, получим:
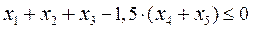
Банк обязан разместить  от кредитов на личные нужды, авто и жилье – на жилье , следовательно: от кредитов на личные нужды, авто и жилье – на жилье , следовательно:
 , упрощая, получим: , упрощая, получим:

Общая доля невозврата по всем кредитам не должна превосходить 0,08, следовательно:
 , упрощая, получим: , упрощая, получим:

Таким образом, математическая модель данной задачи имеет следующий вид:
максимизировать

при следующих ограничениях:
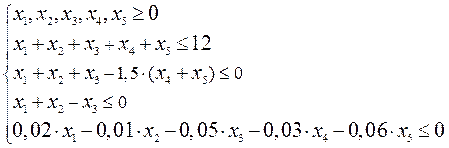
Данная модель является линейной, т. к. целевая функция и ограничения линейно зависят от переменных.
Задача решается в MicrosoftExcelпри помощи команды Сервис
, Поиск решения
. Ячейки Е4:Е8 отведены под значения переменных  , ,  , ,  , ,  , ,  .
В ячейку Е12 введена целевая функция (рис 10.2). .
В ячейку Е12 введена целевая функция (рис 10.2).
Для приведенного на рис 10.1 расчета в соответствующие ячейки введены формулы, показанные на рис. 10.2.

Рисунок 10.1

Рисунок 10.2
В диалоговом окне Поиск решения
введены данные, показанные на рис 10.3 и рис 10.4.

Рисунок 10.3

Рисунок 10.4
Из результатов расчета видно, для того чтобы максимизировать доход, необходимо разместить 7,2 млн $ в кредит на жилье и 4,8 млн $ в кредит на бизнес.
Заключение
В данной работе были рассмотрены примеры решения финансово-экономических задач с использованием функций ПЛТ, ПС и ЧПС, а также оптимизационных задач линейного программирования (планирование производства, транспортная задача, задача о кредитах) с использованием средства Поиск решения в MicrosoftExcel.
Список используемой литературы
1. С.М. Лавренов. Excel. Сборник примеров и задач. – М: Финансы и статистика 2003г. – 335 с.
2. Хемди А. Таха. Введение в исследование операций. – М: Вильямс 2005г. – 901 с.
3. А.Ю. Гарнаев. Использование MSExcelи VBA в экономике и финансах. – СПб: БХВ – Санкт Петербург 2000 г. – 336 с.
4. И.Я. Лукасевич. Анализ финансовых операций. Методы, модели вычислений. – М: Финансы, ЮНИТИ, 1998г. – 400 с.
5. С. Фишер и др. Экономика. – М: Дело Лтд 1995г. – 829 с.
|