МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Харківський національний університет радіоелектроніки
Центр заочної форми навчання
Кафедра Технологій та автоматизації виробництва РЕЗ та ЕОЗ
КУРСОВА РОБОТА
З дисципліни
«Елементи і пристрої інтегрованих систем»
Елементи системи керування зварювальним маніпулятором інтегрованої системи
Виконав:
Перевірив:
2010
Харківський національний університет радіоелектроніки
Центр____ПО_______________ Кафедра _______ТАВР_________
Спеціальність 6.091402 «Гнучкі комп’ютеризовані системи та робототехніка»
ЗАВДАННЯ
на курсовий проект
Студентові ________________________________________________
1. Тема роботи: Розрахунок елементів системи керування зварювальним маніпулятором інтегрованої системи ________________________________________________________________________________________________________________________________
2. Термін здачі студентом роботи_________________________________
3. Вихідні дані до роботи: маніпулятор «Універсал 5.02» з наступними характеристиками: номінальна вантажоздатність – 5 кг; похибка позиціонування - ± 1 мм; тип перетворювача приводу – тиристорний ПТ6-У 5.02; виконуючі елементи ступенів рухливості – електродвигуни постійного струму типу СЛ; електропневморозподілювачі; потужність живлення перетворювача – не більше 1,5 кВт; габаритні розміри перетворювача – 600 х 600 х 800 мм____________________________________________________
4. Зміст пояснювальної записки (перелік питань, які потрібно розробити):
4.1 аналіз технічного завдання;
4.2 динамічні властивості електромеханічного перетворювача струму;
4.3 характеристика промислового роботу «Універсал 5.02»
4.4 розрахунок системи керування маніпулятором;
4.5 дослідження математичної моделі маніпулятора;
4.6 розрахунок АСК електропривода маніпулятора;
4.7 стабілізація механічних коливань
Календарний план
| Номер |
Назва етапів роботи |
Термін виконання етапів роботи |
Примітка |
| 1 |
Аналіз технічного завдання |
| 2 |
Визначення динамічніх властивостей перетворювача |
| 3 |
Складання характеристикі ПР |
| 4 |
Розрахунок СК маніпулятором |
| 5 |
Дослідження мат. моделі |
| 6 |
Розрахунок АСК електропривод. |
| 7 |
Формулювання висновків |
| 8 |
Складання пояснювальної записки до роботи |
| 9 |
Оформлення графічної частини |
Содержание
Введение
1 Анализ технического задания
1.1 Динамические свойства асинхронного электромеханического преобразователя при питании от источника тока
1.2 Характеристика промышленного робота «Универсал-5.02»
2 Расчёт системы управления манипулятором
2.1 Принцип действия системы управления
2.2 Исследование линейной математической модели манипулятора
2.3 Расчёт АСУ электроприводом манипулятора по одной координате
2.4 Структурная схема манипулятора в режиме переноса инструмента
2.5 Моделирование АСУ манипулятором по одной координате
Выводы
Перечень ссылок
Введение
В современном производстве происходят значительные изменения, отражающие революционные достижения в области электроники, механики, информатики. Серийное производство автоматических манипуляторов – промышленных роботов – освобождает человека от ручного низкоквалифицированного и монотонного труда, и в первую очередь в условиях, вредных для здоровья человека.
Тенденции развития робототехники, как одного из основных средств гибкого автоматизированного и автоматического производства, в настоящее время таковы, что преимущественное развитие должны получить промышленные роботы (ПР) для выполнения основных технологических процессов – сборки, сварки, зачистки заготовок и шлифования изделий, окраски, контроля и разбраковки.
Важную роль для перевода производства на новую ступень развития выполняет популяризация современных концепций построения будущих производственных систем, базирующихся на перспективных достижениях науки и техники.
Развитие средств автоматизации, использующих новейшие достижения информатики и вычислительной техники, автоматики и технической кибернетики, позволяет не только осуществить качественный скачок в создании перспективных технологий, но и перейти на более высокий уровень производственных отношений в народном хозяйстве.
Непременным условием успешного использования роботов в модернизируемых производствах является строгая технологическая дисциплина. Роботы во многом влияют на весь технологический цикл, а их функционирование, зависит от строгого соблюдения поставок и всего графика работы оборудования. И там, где этого нет, где не обеспечена технологическая дисциплина, отсутствует профилактика работы оборудования – роботы просто останавливают производственный процесс.
В промышленной робототехнике наибольший эффект, в ближайшей перспективе, может дать концентрированный переход к использованию роботов в качестве основного, а не вспомогательного технологического оборудования для выполнения таких операций, как сварка, окраска, сборка, лазерная обработка, складирование.
Особо следует акцентировать внимание на недальновидных высказываниях некоторых специалистов о разорительности робототехники и других средств гибкой автоматизации производства. Они, как нам думается, основаны на субъективных оценках сегодняшних, далеко не раскрытых возможностях новой техники и на предубеждении к отбору в качестве аргументов лишь неудачных примеров автоматизации производства. Факты из мировой практики полностью опровергают подобные утверждения. Достаточно сказать, что крупнейшие автомобильные компании промышленно развитых стран «Форд», «Дженерал моторс», «Фольксваген», «Ниссан», «Фиат», «Рено» уже подошли к завершению этапа полной роботизации сварочных и окрасочных производств на своих автосборочных заводах и активно приступили к роботизации других производств, включая механосборочные. Сегодня мысль о полном изготовлении автомобиля с помощью роботов уже никому не представляется фантастической.
Цель работы – рассчитать систему управления манипулятором при выполнении сварочных работ.
Объект работы – промышленный робот «Универсал-5.02».
1 Анализ технического задания
1.1 Динамические свойства асинхронного электромеханического преобразователя при питании от источника тока
Преобразователи частоты, обладающие свойствами источника тока, формируют в фазах двигателя токи, которые не зависят от режима работы и параметров двигателя, а определяются только сигналом задания. Схема включения асинхронного двигателя (АД) для этого случая показана на рис. 1.1. В этой схеме двигатель получает питание от трехфазного источника тока. Значение тока определяется напряжением задания тока  , а частота – напряжением , а частота – напряжением  . .
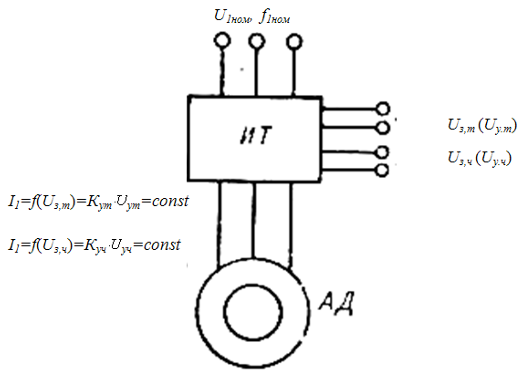
Рисунок 1.1 – Схема питания АД от источника тока
Так как в схеме на рис. 1.1 обмотки статора питаются неизменным током, уравнения механической характеристики запишутся в виде:
 (1.1) (1.1)
При невысоких требованиях к электроприводу можно пользоваться статическими характеристиками АД. При достаточно высоких требованиях к динамическим характеристикам асинхронного электропривода и работе АД на линейном участке статической механической характеристики целесообразно пользоваться понятием динамической механической характеристики, уравнение которой имеет вид:
 ,(1.2) ,(1.2)
или
 ,(1.3) ,(1.3)
где  – момент АД, – момент АД, 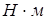 ; ;  – электромагнитная постоянная времени, с; – электромагнитная постоянная времени, с;

производная момента по скорости в точке, относительно которой анализируется динамический процесс. Другими словами,  – это модуль жесткости линеаризированной механической характеристики и может быть определена по формуле: – это модуль жесткости линеаризированной механической характеристики и может быть определена по формуле:
 .(1.4) .(1.4)
В системе преобразователь частоты – двигатель (ПЧ-АД) (рис. 1.1):
 ,(1.5) ,(1.5)
где  – число пар полюсов двигателя. – число пар полюсов двигателя.
Постоянная времени  рассчитывается по уравнению: рассчитывается по уравнению:
 .(1.6) .(1.6)
Структурная схема асинхронного электромеханического преобразователя, линеаризированного в пределах рабочего участка механической характеристики, показана на рис. 1.2.
Рисунок 1.2 – Структурная схема линеаризированного асинхронного механического преобразователя.
При высоких требованиях к электроприводу и широком диапазоне изменения параметров следует пользоваться полной системой (1.1). Дополнив уравнения (1.2 – 1.6) уравнением движения электропривода, получим систему уравнений, которой соответствует представленная на рис. 1.3 структурная схема системы ПЧ-АД (ИТ-АД).
Параметры  и и  в этой структуре должны соответствовать требуемому режиму работы электромеханического преобразователя: в этой структуре должны соответствовать требуемому режиму работы электромеханического преобразователя:  или или 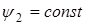 . .

Рисунок 1.3 – Структурная схема линеаризированной системы ИТ-АД.
1.2 Характеристика промышленного робота «Универсал-5.02»
Промышленный робот «Универсал-5.02» относится к классу универсальных и может быть использован для автоматизации погрузочно-разгрузочных работ при выполнении различных технологических операций, в том числе при выполнении сварочных работ.
Промышленный робот «Универсал-5.02» представляет собой автоматическую машину, состоящую из исполнительного устройства в виде манипулятора У-5.02 с шестью степенями подвижности (рис. 1.4), перепрограммируемого устройства программного управления АСП-1 с силовым преобразователем ПТ6-У.5.02 для выполнения в производственном процессе управляющих и двигательных функций.

Рисунок 1.4 – Кинематическая схема манипулятора «Универсал-5.02»
Управление такой машиной требует реализации характерных алгоритмов разгона-замедления степеней подвижности, адаптации к нагрузке путем автоматической или полуавтоматической коррекции параметров следящего контура для обеспечения заданного качества процесса позиционирования.
Так как скорости перемещения захватного устройства манипулятором весьма значительны и достигают 1м/с, а требования к погрешности позиционирования при выполнении сварочных работ, не должны превышать 0,02%, решение этой задачи представляет определенные трудности.
Для решения этой задачи следует привести основные типоразмеры электропривода по величине номинального момента  и, соответствующие им, типы асинхронных двигателей, моменты инерции ротора, номинальные и максимальные частоты вращения привода (табл. 1.1). и, соответствующие им, типы асинхронных двигателей, моменты инерции ротора, номинальные и максимальные частоты вращения привода (табл. 1.1).
Таблица 1.1 – Типоразмеры электропривода
| Наименование параметров |
Норма |
Допустимое отклонение, % |
| Тип двигателя |
4АХБ2П90L4ПБ |
4АХБ2П100L4ПБ |
| Номинальный момент, МН, Н*м |
7 |
17 |
±15 |
| Момент инерции ротора, кг*м2*10-2 |
0,56 |
1,12 |
– |
| Номинальная частота вращения, nн, об/мин |
600 |
| Максимальная частота вращения, nmax, об/мин |
1000 |
Максимальный момент привода  при переходных процессах не больше чем: 2 при переходных процессах не больше чем: 2 . На максимальной частоте вращения электропривод развивает момент не менее 0,6 . На максимальной частоте вращения электропривод развивает момент не менее 0,6 . .
Управляющее напряжение меняется от минус 10 до 10В. Амплитуда пульсаций не более  . .
Минимальный коэффициент усиления замкнутой по положению системы управления 30с-1 при частоте квантования в контуре положения не менее 100 Гц.
В современных отечественных конструкциях промышленных роботов, выпускаемых серийно, предусмотрено автоматическое формирование характеристики разгона-торможения каждой степени подвижности манипулятора по параметрам, заданным оператором в процессе обучения, регулировки робота.
В качестве параметров, как правило, используются характерные точки траектории разгона-замедления: точки начала разгона-замедления, точка в окрестности окончания процесса позиционирования или промежуточные точки в случае необходимости задания специальной траектории. По заданным точкам устройство управления формирует траекторию разгона-торможения, которая в общем случае может аппроксимироваться отрезками прямых или частями параболы. Параболическая форма траектории обеспечивает движение координаты с постоянным ускорением и минимальное время разгона замедления. Однако в окрестностях точки позиционирования траектория имеет форму отрезка прямой, что обеспечивает плавный подход к точке и исключает перерегулирование, что улучшает качество сварного шва.
Указанная регулировка осуществляется оператором при наладке промышленного робота и производится при определенных условиях: номинальной статической нагрузке манипулятора, нормальной окружающей температуре, стандартном положении подвижных органов манипулятора, указанном в технических условиях, а также отсутствия изгиба сварочного электрода. При этом предполагается, что наладка обеспечивает работоспособность робота с учётом изменения указанных факторов в допустимых пределах.
Однако, как показала практика использования роботов в сварочных работах, возникает необходимость регулировки параметров следящего контура управления степенями подвижности манипулятора в режиме переноса инструмента (электрода), что связано с его плавлением, т.е. уменьшением физических размеров и специфическими условиями применения (качества сварной поверхности и т.д.).
Настоящая квалификационная работа посвящена специализированным вопросам настройки и регулировки двигательных функций промышленного робота «Универсал-5.02» при выполнении сварочных работ.
2 Расчёт системы управления манипулятором
2.1 Принцип действия системы управления
Система управления (СУ) асинхронным электроприводом реализована в соответствии с частотно-токовым способом управления, что позволяет получать глубокое регулирование угловой скорости при высоких динамических показателях. При частотно-токовом управлении в обмотки электрической машины вводятся токи, мгновенные значения которых определяются требуемым значением электромагнитного момента и угловым положением ротора машины. Для этого на вход привода подаются два независимых входных сигнала, задающих токи в обмотках и обеспечивающих не только регулирование момента, но и возможность устанавливать требуемый поток намагничивания и реактивный ток преобразователя.
На вход преобразователя поступают сигнал  задания тока (потока) возбуждения и сигнал задания тока (потока) возбуждения и сигнал 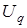 регулирования момента, получаемый в результате сравнения напряжения задания скорости регулирования момента, получаемый в результате сравнения напряжения задания скорости  с напряжением с напряжением  , пропорциональным действительному значению скорости. , пропорциональным действительному значению скорости.
Задание амплитуды и фазы тока статора  выполняется в соответствии с выражениями выполняется в соответствии с выражениями
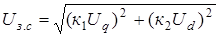 ;(2.1) ;(2.1)
 ,(2.2) ,(2.2)
где  – коэффициенты пропорциональности. – коэффициенты пропорциональности.
Пропорциональная сигналу 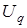 частота скольжения частота скольжения  суммируется с частотой вращения ротора суммируется с частотой вращения ротора  и в виде импульсных сигналов с частотой и в виде импульсных сигналов с частотой  используется для формирования сигналов задания фазовых токов используется для формирования сигналов задания фазовых токов 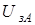 и и  частотой частотой  с учетом фазового сдвига с учетом фазового сдвига 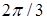 . Здесь . Здесь  – опорный сигнал частотой 2 кГц, – опорный сигнал частотой 2 кГц,  – число пар полюсов. Сигнал, пропорциональный частоте вращения поля в статоре – число пар полюсов. Сигнал, пропорциональный частоте вращения поля в статоре  электродвигателя М, формируется с помощью датчика угла, выполненного в виде фазовращателя. Изменение фазы фазовращателя преобразуется в код частоты вращения, поступающий на цифро-аналоговый преобразователь (ЦАП). Аналоговый сигнал электродвигателя М, формируется с помощью датчика угла, выполненного в виде фазовращателя. Изменение фазы фазовращателя преобразуется в код частоты вращения, поступающий на цифро-аналоговый преобразователь (ЦАП). Аналоговый сигнал  с выхода ЦАП реализует обратную связь по скорости. Трехфазный регулятор тока и транзисторный инвертор формируют в статоре двигателя М токи, пропорциональные сигналам с выхода ЦАП реализует обратную связь по скорости. Трехфазный регулятор тока и транзисторный инвертор формируют в статоре двигателя М токи, пропорциональные сигналам 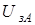 , ,  и ток в фазе С, равный сумме токов фаз А и В. выполненный на терморезисторах датчик температуры служит для формирования сигнала “Превышение допустимой температуры АД” и сигнала, ограничивающего момент двигателя путем воздействия на задатчик частоты скольжения. и ток в фазе С, равный сумме токов фаз А и В. выполненный на терморезисторах датчик температуры служит для формирования сигнала “Превышение допустимой температуры АД” и сигнала, ограничивающего момент двигателя путем воздействия на задатчик частоты скольжения.
2.2 Исследование линейной математической модели манипулятора
Анализ и синтез линейных систем, в настоящее время, производится одним из двух основных методов. Первый метод основывается на применении преобразований Лапласа, передаточных функциях, структурных схемах и графах, второй (метод пространства состояния) – на описании и моделировании систем в пространстве состояния.
В пространстве состояния непрерывные системы описываются системой дифференциальных уравнений первого порядка, которые называют уравнениями состояния. При этом используются методы матричного исчисления и векторного анализа.
В данной работе применим метод пространства состояния, используя рекомендации, данные в [43].
2.3 Расчёт АСУ электроприводом манипулятора по одной координате
Современные роботизированные сварочные комплексы включают в себя один или несколько сварочных промышленных роботов и один или два поворотных стола – позиционера. В отечественной промышленности для сварки применяют различные типы ПР, в том числе ПР серии «Универсал».
В данной работе под моделью манипулятора понимается модель механизма перемещения инструмента (электрода) сварочного робота “Универсал” по одной из координат X, Y или Z.
Механизм включает в себя:
выход системы управления;
электропривод перемещения, состоящий из контуров положения и скорости, и силовой части;
механическая часть механизма от выходного вала двигателя электропривода до мечта установки электродвигателя следующей координаты или места установки технологических приводов сварочного инструмента.
По принципу построения манипуляторы с управлением от ЭВМ и импульсной схемой преобразования сигналов управления асинхронным двигателем с частотно-токовым управлением (ЧТУ) являются дискретными системами автоматического управления (САУ), однако, учитывая, что реальная полоса пропускания манипулятора ( ), в рабочем режиме значительно меньше частоты дискретизации по управлению ( ), в рабочем режиме значительно меньше частоты дискретизации по управлению ( ) и тем более по частотам преобразования в АСУ электроприводом ( ) и тем более по частотам преобразования в АСУ электроприводом ( ), такую систему, в первом приближении, можно рассматривать как непрерывную. ), такую систему, в первом приближении, можно рассматривать как непрерывную.
Основными нелинейностями манипулятора являются – ограничитель напряжения на выходе регулятора скорости, нелинейности преобразования сигнала в электроприводе с ЧТУ и механические люфты и ограничения механизмов перемещения платформы. Однако, если работу АСУ электроприводом рассматривать раздельно в режиме переноса инструмента (нелинейный режим с ограничением) и в режиме слежения за технологическим процессом (линейный режим) и пренебречь малыми, к тому же сглаживаемыми, нелинейностями преобразования сигналов в электроприводе, а также пренебречь малыми механическими нелинейностями (механическая часть тщательно обрабатывается и не включена в обратную связь контура управления), то каждый режим отдельно, в первом приближении можно считать линейным.
Данные предположения использованы при дальнейших расчётах.
Передаточная функция силовой части электропривода имеет вид:
 ,(2.3) ,(2.3)
где  – коэффициент усиления привода с ЧТУ; – коэффициент усиления привода с ЧТУ;  – постоянная времени силовой цепи ИТ-АД, с. – постоянная времени силовой цепи ИТ-АД, с.
 ,(2.4) ,(2.4)
где  – статический коэффициент передачи привода, – статический коэффициент передачи привода, 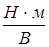 ; ;  – масштабный коэффициент преобразования скорости поворота ротора АД в напряжение, – масштабный коэффициент преобразования скорости поворота ротора АД в напряжение,  ; ;  – коэффициент, учитывающий увеличение момента инерции системы за счет нагрузки, приведенной к валу АД; – коэффициент, учитывающий увеличение момента инерции системы за счет нагрузки, приведенной к валу АД;  – момент инерции АД, – момент инерции АД,  . .
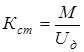 (2.5) (2.5)

 (2.6) (2.6)
 . .
Следовательно,
 (2.7) (2.7)
Подставив рассчитанные параметры в (2.3), получим:
 . .
2.4 Структурная схема манипулятора в режиме переноса инструмента
Данный режим работы манипулятора является нелинейным. Этот режим используется для быстрого переноса технологического инструмента (сварочного электрода) из исходной зоны – в рабочую. Структурная схема контура скорости для режима переноса инструмента показана на рис. 2.1.
В этом режиме ограничитель на выходе ПИ (пропорционально-интегрального) регулятора скорости входит в режим ограничения и тем самым размыкает обратную связь по скорости и остается только характерная для частотно-токового управления обратная связь через задатчик тока и контур тока.

Рисунок 2.1 – Структурная схема контура скорости в режиме переноса инструмента
Амплитуда тока статора в этом режиме формируется задатчиком тока пропорционально  , а частота изменения тока равна: , а частота изменения тока равна:
 ,(2.8) ,(2.8)
где  – частота вращения робота двигателя; – частота вращения робота двигателя;  – частота скольжения, что обеспечивает в установившемся режиме заданный момент и скорость вращения ротора. – частота скольжения, что обеспечивает в установившемся режиме заданный момент и скорость вращения ротора.
Передаточная функция для этого режима:
  (2.9) (2.9)
где  – заданная угловая скорость двигателя, пропорциональная – заданная угловая скорость двигателя, пропорциональная  . .
Рассмотрим контур положения (КП), структурная схема которого в режиме переноса инструмента показана на рис. 2.2, где приняты следующие обозначения:
 – заданная скорость переноса инструмента, – заданная скорость переноса инструмента,  ; ;
 – заданное положение переноса; – заданное положение переноса;
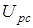 – сигнал с регулятора скорости (РС); – сигнал с регулятора скорости (РС);
ЭС – элемент сравнения.

Рисунок 2.2 – Структурная схема КП в режиме переноса инструмента
В режиме переноса на привод подается сигнал номинальной скорости переноса  и конечное положение режима по грубой шкале (с точностью до 0,5 оборотов вала двигателя) – и конечное положение режима по грубой шкале (с точностью до 0,5 оборотов вала двигателя) –  . Контур положения в этом режиме замкнут через счетчик оборотов. Сигнал со счетчика оборотов ( . Контур положения в этом режиме замкнут через счетчик оборотов. Сигнал со счетчика оборотов ( ) сравнивается с сигналом ) сравнивается с сигналом  и при их совпадении режим переноса через ключ и при их совпадении режим переноса через ключ  отключается и через ключи отключается и через ключи  и и  с заданной задержкой включается режим слежения. с заданной задержкой включается режим слежения.
Передаточная функция в режиме переноса инструмента по положению равна:
  (2.10) (2.10)
Подставив численные значения в (2.9) и (2.10) получим:
При 
 . .
При 
 . .
При 
 . .
При 
 . .
Составим структурную схему механической части манипулятора по одной координате.
Механическая часть между валом двигателя и последующей подвижной платформой или инструментом имеет упругие связи и люфты, что приводит к механическим колебаниям инструмента при набросе (или снятии) скачка нагрузки. Не вдаваясь детально во все причины возникновения этих колебаний, в соответствии с [11], [44], [45] и др., в первом приближении, примем, что механические колебания по каждой координате описываются дифференциальным уравнением 2-го порядка.
Для дальнейших расчетов примем [7], [34]:  ; ;  . .
Рисунок 2.3 – Структурная схема механической части манипулятора по одной координате
2.5 Моделирование АСУ манипулятором по одной координате
Уравнения состояния в векторно-матричной форме записи имеют следующий вид:
 , (2.11) , (2.11)
где  – матрица состояния (динамическая); – матрица состояния (динамическая); 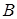 – матрица управляющих воздействий (матрица входа). – матрица управляющих воздействий (матрица входа).
Для определения элементов матрицы  и и 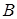 составим схемы моделирования, в соответствии с алгоритмической схемой (рис. 2.2). составим схемы моделирования, в соответствии с алгоритмической схемой (рис. 2.2).
Рассмотрим контур скорости.
Режим разгона при переносе инструмента 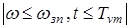 иллюстрируется схемой модели на рис. 2.4. иллюстрируется схемой модели на рис. 2.4.

Рисунок 2.4 – Схема моделирования скорости в режиме переноса инструмента
Дифференциальные уравнения в режиме переноса инструмента примут вид:

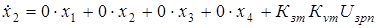 (2.12) (2.12)

 . .
Следовательно:
  . (2.13) . (2.13)
После подстановки в (2.13) численных значений, получим

 . .
Режим переноса инструмента при  ( ( ) описывается уравнением: ) описывается уравнением:
  . (2.14) . (2.14)
Схему моделирования контура положения в режиме переноса электрода построим на рис. 2.5.

Рисунок 2.5 – Схема моделирования контура положения в режиме переноса электрода
Дифференциальное уравнение режима разгона при переносе инструмента  имеет вид: имеет вид:


 (2.15) (2.15)

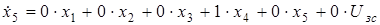 . .
Получим матрицы  и и 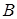
  . (2.16) . (2.16)
После подстановки численных значений матрицы  и и 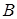 примут вид: примут вид:
  . .
Схему математической модели механической части манипулятора по одной координате составим в соответствии с ее структурной схемой (рис. 2.3).

Рисунок 2.6 – Схема моделирования механической части манипулятора по одной координате
В режиме переноса инструмента при разгоне  , следует принять: , следует принять:
 (2.17) (2.17)
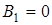 ; ;  , ,
а после разгона:

 ; ;  . .
Графики переходных процессов показаны на рис. 2.7 – 2.10.

Рисунок 2.7 – Переходный процесс по скорости электрода, под нагрузкой

Рисунок 2.8 – Переходной процесс по положению электрода, под нагрузкой
Выводы
В процессе выполнения бакалаврской квалификационной работы, была достигнута её цель, заключающаяся в расчёте системы управления манипулятором промышленного робота «Универсал-5.02» при выполнении сварочных работ.
В первом разделе дипломной работы, после изучения специальной литературы был проведен анализ технического задания, включающий:
– приведение основных понятий и определений робототехники;
– динамические свойства асинхронного электромеханического преобразователя при питании от источника тока;
– характеристики промышленного робота «Универсал-5.02».
Во втором разделе работы, после детального изучения принципа действия, был произведен расчёт системы управления манипулятором, включающий следующие этапы:
– исследование линейной математической модели манипулятора;
– расчёт АСУ электроприводом манипулятора по одной координате;
– составление структурной схемы манипулятора в режиме переноса инструмента;
– моделирование АСУ манипулятором по одной координате;
– стабилизацию механических колебаний манипулятора при сварочных работах.
Результатом работы стала модель системы управления манипулятором, удовлетворяющая техническим требованиям, выдвигаемым к выполнению сварочных работ, а именно: необходимая точность позиционирования электрода достигается через 1,5 с, при этом – амплитуда колебаний шва не превышает 3 – 4% от планируемой траектории.
Перечень ссылок
1. Гантмахер Ф.Р. Лекции по аналитической механике. – М.: Физматгиз, 1960.
2. Парс Л. Аналитическая динамика / Пер. с англ. – М.: Наука, 1971.
3. Лурье А.И. Аналитическая механика. – М.: Физматгиз, 1961.
4. Козлов В.В., Макарычев В.П., Тимофеев А.В., Юревич Е.И. Динамика управления роботами. – М.: Наука, 1984.
5. Попов Е.П., Верещагин А.Ф., Зенкевич С.Л. Манипуляционные роботы: динамика и алгоритмы. – М.: Наука, 1980.
6. Виттенбург И. Динамика систем твердых тел / Пер. с англ. – М.: Мир, 1980.
7. Вукобратович М., Стокич Д. Управление манипуляционными роботами: теория и приложения / Пер. с серб.-хорв. – М.: Наука, 1993.
8. Пол Р. Моделирование, планирование траекторий и управление движением робота-манипулятора / Пер. с англ. – М.: Наука, 1976.
9. Белецкий В.В. Двуногая ходьба. Модельные задачи динамики и управления. – М.: Наука, 1994.
10. Охоцимский Д.Е., Голубев Ю.Ф. Механика и управление движением автоматического шагающего аппарата. – М.: Наука, 1984.
11. Алферов Г.А., Кулаков Ф.М., Неокесарийский В.Н. Кинематические и динамические модели исполнительной системы робота. – Л.: ЛГУ, 1983.
12. Бордюг Б.А., Ларин В.Б., Тимошенко А.Г. Задачи управления шагающими аппаратами. – К.: Наукова думка, 2004.
13. Слиеде П.Б., Аузиньш Я.Н., Иткин В.М. Алгоритм расчета на ЭЦВМ колебательных характеристик манипуляционных роботов // Машиноведение. – 1984. – №2 .
14. Формальский А.М. Перемещение антропоморфных механизмов. – М.: Наука, 1992.
15. Иовлев В.Ю., Смольников Б.А. Исследование колебательных свойств двузвенного робота // Робототехника. – Л.: ЛПИ, 1977.
16. Корытко О.Б., Юдин В.И. К расчету собственных частот манипулятора промышленного робота в общем случае // Управление робототехническими системами и их очувствление. – М.: Наука, 1983.
17. Судникович Г.Б., Челпанов И.Б. Задачи и методы определения упругих колебаний манипуляторов // Динамика управляемых колебательных систем. – Иркутск: ИПИ, 1983.
18. Вукобратович М., Потконяк В. Численный метод моделирования динамики манипулятора с упругими свойствами // Изв. АН СССР. Техн. Кибернетика. – 1991. – №5.
19. Слиеде П.Б., Аузиньш Я.Н., Иткин В.М. Алгоритмы математического имитационного моделирования упругих манипуляторов на ЭЦВМ // Symposium Grundlagen der Dynamik und Steuerung von Industriorobotern. Vortrage. Band. 1. – Berlin, 1985.
20. Сунада В., Дубовски С. Применение метода конечных элементов к динамическому анализу гибких пространственных и плоскопараллельных систем // Контруирование и технология машиностроения. – 1981. – №3.
21. Сунада В., Дубовски С. Об исследовании динамических характеристик промышленных роботов-манипуляторов с упругими звеньями // Конструирование и технология машиностроения. 1983. – №1.
22. Якубович В.А. Адаптивное управление манипуляторами с массовыми приводами // Робототехника. – Л.: ЛПИ, 1988.
23. Хейман Б., Лоозе Х., Шмидт К.Д., Роте Х., Любушин А.А. Динамика и оптимальное управление роботами-манипуляторами // Успехи механики. – 1984. – Т.7. Вып. 4.
|