Министерство образования республики Беларусь
Учреждение образование «Гомельский Государственный университет им. Ф.Скорины »
Математический факультет
Кафедра математического анализа
Допущена к защите
Зав. кафедрой _______ Малинковский Ю.В.
«___» ___________ 2002г.
Формирование понятия функции в курсе математики средней школы
Дипломная работа
Исполнитель
студентка группы М-61 _________ Рыкунова Юлия Витальевна
Научный руководитель _________Гаврилюк Александр Владимирович
к. п.н., доцент
Рецензент _________ Лытко Александр Александрович
к. п.н., доцент
Гомель 2002
Содержание:
Введение
§1 Различные трактовки понятия функции в школьном курсе математики.
§2 Функция и задание ее аналитическим выражением.
§3 Область определения функции и область значений функции как принципиально важные понятия в определении функции.
§4 Важнейшие классы функций: четные, конечные периодические.
§5 Тестовые работы по теме «Числовые функции. Четные и нечетные функции. Периодические функции»
Заключение.
Введение
Функция – одно из фундаментальных понятий математики, а функциональная идея является одной из определяющих идей развития школьного курса математики.
Данная дипломная работа посвящена анализу изучения понятия функции в школьном курсе математики. Основная ее цель – выявить ключевые моменты в определении этого понятия, на которые необходимо обратить особое внимание школьников при изучении данной темы, для того, чтобы не допустить формального усвоения данного понятия. В существующей школьной литературе (исключение составляет учебник «Алгебра» 8-11 класс К.О. Ананченко, Н.Т. Воробьева, Г.Н. Петровского) преобладает традиционная методика в изложении понятия функции, которая приводит к тому, что в результате выпускник школы, давая стандартное определение функции, не может ответить на элементарные вопросы, относящиеся к этой теме. В частности, на вопрос: «Какая функция называется  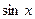 ?», правильный и полный ответ можно услышать очень редко. ?», правильный и полный ответ можно услышать очень редко.
Работа состоит из 5 параграфов, введения и заключения.
В § 1 дается анализ двух основных трактовок понятия функции, имеющихся в рекомендованной школьной литературе: так называемое классическое
, ориентированное в основном на приложение математики в физике и технике и опирающееся на понятие «переменная величина», и современное
(или теоретико - множественное), связанное с отказом от расплывчатого понятия переменной величины, которое позволяет значительно расширить понятие функции, так как рассматривает функции не только от «величин».
В § 2 рассматриваются вопросы, связанные со способами задания функции. Ключевым моментом этого параграфа является анализ аналитического способа задания функций, т.е. с помощью формулы. Важным в этом параграфа является исследование соотношения понятий «функция» и «формула».
В третьем параграфе дается ответ на важный вопрос: «Что значит задать функцию?» Здесь речь в большей степени идет о множестве определения и множестве значений функций и важности понимания того, что говорить о функции, информация об области, определения которой отсутствует, не корректно. Следует отметить, что непонимание этого факта часто присутствует в ответах даже подготовленных школьников.
В § 4 рассматриваются важные классы функций: четные, нечетные, периодические. Здесь определения данных классов подкреплены типичными примерами, в которых школьники, как правило, делают ошибки. Основное внимание уделено на то, что при определении таких функций кроме закона соответствия важно следить и за их областью определения.
В § 5 подготовлен комплект тестовых заданий по теме «Числовые функции. Сложная функция. Четные, нечетные функции. Периодические функции». При разработке данного комплекта тестовых заданий учитывались следующие моменты:
1) содержание заданий, вопросов охватывает наиболее принципиальные стороны и идеи темы;
2) в заданиях сделан акцент и на проверку навыков, и на выявление глубины освоения идейного содержания темы, проявлению математической эрудиции;
3) по усмотрению учителя тестовое задание может предлагаться ученикам не полностью, а частями.
4) задания обеспечивают возможность проведения итоговых занятий на заключительном этапе изучения понятия функции в школьном курсе математики.
Комплект тестовых заданий составлен в четырех вариантах и включает двенадцать вопросов. На каждый из них дается четыре ответа для выбора правильного из них. Вопросы в заданиях предлагаются в текстовой и графической формах. Задания рассчитаны на 45 минут работы школьника.
В процессе работы над дипломной работой была проанализирована основная литература по данной теме, список которой приводится в конце. Отметим, что среди этой литературы, на мой взгляд, учебник «Алгебра» 8-11 класс К.О. Ананченко, Н.Т. Воробьева, Г.Н. Петровского в наибольшей степени соответствует современным требованиям в подходе к освещению затронутых в нашей работе вопросов.
В заключении отметим, что в данной работе сделана попытка, опираясь на основные школьные учебники, собрать материал по данной теме, систематизировать его для того, чтобы выделить важные моменты при формировании понятия функции и препятствовать формальному усвоению понятий, сопутствующих определению функции. Большую роль в достижении этой цели играют разработанные тестовые задания, разбор типичных примеров, в которых учащиеся зачастую дают неправильные ответы.
Данная работа охватывает весь материал, связанный с понятием функции в школьном курсе и может быть использована при работе на уроках в обычных, профильных классах и на факультативных занятиях по математике.
§1. Различные трактовки понятия функции в школьном курсе математики
Функция – одно из фундаментальных понятий математики, а функциональная идея является одной из определенных идей развития школьного курса математики.
В существующих программах по математике как для школ (классов) с углубленным изучение математики, так и для базовых школ тема «Функции» занимает большой объем, к тому же очень много вопросов, касающихся функций, содержит программа по математике для поступающих в ВУЗы, поэтому особенно важен вопрос о трактовке этого фундаментального понятия математики.
Существуют различные трактовки общего понятия функции. В математике известны два основных направления: так называемое классическое
, ориентированное в основном на приложение математики в физике и технике и опирающееся на понятие «переменная величина», и современное
(или теоретико - множественное), связанное с отказом от расплывчатого понятия переменной величины, которое позволяет значительно расширить понятие функции, так как рассматривает функции не только от «величин».
Примером классического направления трактовки функции может служить определение функции: «зависимость одной переменной от другой, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной, называют функциональной зависимостью,
илифункцией.
Независимую переменную иначе называют аргументом
, а о зависимой переменной говорят, что она является функцией
от такого аргумента. “ (Алгебра, учебник для седьмого класса общеобразовательных учреждений. Под редакцией С.А. Теляковского, М., 1997, стр. 44). Авторы учебника «Алгебра» для 9 класса общеобразовательных школ с углубленным изучением математики К.О. Ананченко, Н.Т. Воробьева, Г.Н. Петровского, Мн, 1995г., дают общее понятие функции в двух трактовках. С одной стороны они истолковывают функцию как «соответствие (правило) по которому для любого х (независимой переменной) из множества Х сопоставляется вполне определенное (единственное) у (зависимая переменная) из Y (стр.4)
С другой стороны, они определяют функцию как соответствие между множествами: если Х и Y – два произвольных множества, то говорят, что на Х определена функция f, принимающая значения из Y, если каждому элементу х 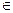 Х поставлен в соответствие единственный элемент y Х поставлен в соответствие единственный элемент y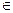 Y “ /стр. 5/. Y “ /стр. 5/.
Это уже второе современное (теоретико – множественное) направление.
§2. Функция и задание её аналитическим выражением
Задать функцию – это значит указать область ее определения и соответствие (правило), при помощи которого по данному значению аргумента находятся соответствующие ему значения функции.
Из всех основных способов задания функции, таких, как аналитический, табличный, графический, алгоритмический или программный, особый интерес и значимость имеет задание функции при помощи некоторой формулы, некоторого аналитического выражения, позволяющего для любого значения аргумента из области определения Х, находить соответствующее значение функции путем вычислений.
Представление о формуле как о некоторой формуле, связывающей y и х, к сожалению, довольно часто встречается у школьников. Функция и формула - это разные «вещи» Одно дело-функция как отображение одного множества (в данном случае числового множества) на другое, другое дело – формула, представляющая собой лишь один из способов задания функции.
Чем же опасно отождествление функции с формулой, которая описывает функцию?
Во-первых, не всякая формула задает функцию.
Приведем несколько примеров:
у = 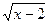 + + ; y = ; y = 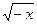 + +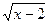 : :
y =  + +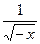 ; и т.д. ; и т.д.
Что можно сказать об области определения, например, функции
y= 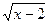 + + ? ?
Функция у = 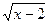 имеет область определения [2; + имеет область определения [2; +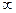 ), а функция у = ), а функция у =  - область определения ]- - область определения ]-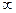 ; 1]. Указанные промежутки не пересекаются, значит, формула у = ; 1]. Указанные промежутки не пересекаются, значит, формула у = 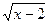 + + не определяет никакой функции. не определяет никакой функции.
Во всех указанных примерах за формулой не стоит никакой функции, так как область определения выражений f(x) есть пустое множество.
Во-вторых, не всякую функцию можно задать с помощью формулы.
Примером такой функции является функция Дирихле, определенная на числовой прямой:
D(y) = 
Эта функция есть отображение множества рациональных чисел в единицу и множества иррациональных чисел в нуль.
В-третьих, несколько формул могут задавать одну-единственную функцию.
Пример:
у = 
Эта функция определена на всей числовой прямой, т.е. D(y) = (-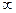 ;+ ;+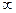 ) и задана с помощью трех аналитических выражений, а именно на промежутке (- ) и задана с помощью трех аналитических выражений, а именно на промежутке (-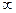 ;0) используется закон числового соответствия, описываемый формулой у = 2, на отрезке [0;2] – формулой 1+x ;0) используется закон числового соответствия, описываемый формулой у = 2, на отрезке [0;2] – формулой 1+x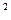 , а на промежутке (2;+ , а на промежутке (2;+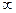 ) – формулой у = х-1. ) – формулой у = х-1.
Таким образом, формула – это не сама функция, а всего лишь один из способов ее задания.
§3. Область определения функции и область значений функции как принципиально важные понятия в определении функции
Принципиально важным вопросом при формировании понятия функции является вопрос об области определения функции и области значений функции. Из определения функции вытекает, что функция у = f(x) должна задаваться вместе с ее областью определения Х. При этом подчеркнем, что область определения функции может задаваться либо условиями решаемой задачи, либо физическим смыслом изучаемого явления, либо математическими соглашениями.
Напоминаем, что областью определения функции (обозначается D(f) или D(y)) называется множество Х, на котором определяется функция f.
Например, функция, выражающая зависимость между пройденным путем и временем движения при свободном падении тела, брошенного без начальной скорости, определяется как
f (x) =  , D(f) = [0; , D(f) = [0; ] ]
Для х>0 данная функция не определена, так как время движения не может быть отрицательным. В то же время формула f (x) =  имеет смысл при всех х имеет смысл при всех х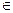 R. R.
Заметим, что если функция задана формулой у = f(x) и область определения не указана, то считают, что область определения функции совпадает с областью определения выражения f(x), т.е. множеством тех значений х, при которых выражение имеет смысл.
Важным в формировании понятия функции является понимание следующего принципиального момента. За счет за счет варьирования области определения функции можно при желании задать сколь угодно много разных функций, используя одну и ту же формулу.
Пример:
у = 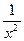 , ,
определенная на отрезке [-6;-1], у = 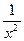 , определенная на промежутке (0;+ , определенная на промежутке (0;+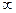 ), это разные функции. ), это разные функции.
Косинус, определенный, например, на отрезке [0;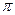 ], косинус, определенный на отрезке [ ], косинус, определенный на отрезке [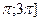 , и косинус, определенный на всей числовой прямой, - это три различные функции. Областью значений функции, или областью изменения функции (обозначается Е(f) или Е(у)) называется множество всех у изY, для каждого из которых существует хотя бы одно значение аргумента х, такое, что f(x) = y. , и косинус, определенный на всей числовой прямой, - это три различные функции. Областью значений функции, или областью изменения функции (обозначается Е(f) или Е(у)) называется множество всех у изY, для каждого из которых существует хотя бы одно значение аргумента х, такое, что f(x) = y.
Область изменения функции у = f(x) вычисляется по уже заданной области определения.
Рассмотрим примеры:
1. Пусть дана функция

y =  . .

Найдем область определения этой функции: D(y) состоит из всех тех действительных чисел, для которых log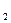 sinx sinx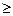 0 и sinx>0. Так как 0 и sinx>0. Так как 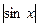 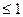 , то для 0 < sinx < 1 log , то для 0 < sinx < 1 log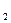 sinx < 0, поэтому чтобы найти область определения данной функции достаточно решить уравнение sinx < 0, поэтому чтобы найти область определения данной функции достаточно решить уравнение
log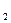 sin x = 0 sin x = 0
log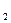 sin x = log sin x = log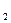 1 1
sin x = 1, откуда
x =  + 2 + 2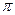 n, n n, n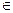 Z. Z.
Таким образом, D(y) = { +2 +2 n , n n , n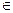 Z}. Z}.
Легко видеть, что область изменения функции E(y) = {0}, поскольку
log sin ( sin ( + 2 + 2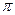 n) = log n) = log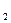 1 = 0. 1 = 0.
2. Найти область изменения функции
у = 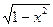 . .
Решение:
Составим уравнение 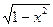 = а, и исследуем множество его решений. = а, и исследуем множество его решений.
При а  0 возведём обе части данного уравнения в квадрат, получим равносильное уравнение 1- х 0 возведём обе части данного уравнения в квадрат, получим равносильное уравнение 1- х = а = а или х или х = 1 - а = 1 - а . Это уравнение имеет решение лишь при 1 - а . Это уравнение имеет решение лишь при 1 - а 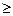 0, откуда а 0, откуда а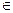 [-1;1], но с учетом, а [-1;1], но с учетом, а 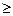 0 исходное уравнение имеет решение тогда и только тогда, когда а 0 исходное уравнение имеет решение тогда и только тогда, когда а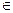 [0;1], поэтому E(y) = [0;1]. [0;1], поэтому E(y) = [0;1].
3. Найти область определения функции
y = 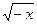 + +  . .
Решение:
Функция y = = 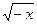 определена для значений x определена для значений x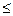 0; 0;
Функция y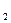 = =  определена для значений 4+x определена для значений 4+x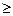 0; 0;
Т.е. x>-4. Следовательно, общей частью двух областей является промежуток x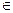 (-4;0]. Он и есть область определения данной функции. (-4;0]. Он и есть область определения данной функции.
Заметим, что если данная функция есть сумма (разность, произведение) других функций, то её область определения есть пересечение множеств, являющихся областями определения и исходных функций.
§4. Важнейшие классы функций: четные, нечетные, периодические
Говорят, что множество Х
симметрично относительно нуля (симметрично относительно начала координат), если множество Х
таково, что (-х)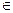 Х
для любого х Х
для любого х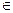 Х
, т.е. вместе с каждым своим элементом х, оно содержит и ему противоположный элемент (-х). Х
, т.е. вместе с каждым своим элементом х, оно содержит и ему противоположный элемент (-х).
Примеры симметричных относительно нуля множеств:
отрезок [-5;5];
интервал [-3;3];
числовая прямая (- ); );
Примеры несимметричных множеств:
отрезок [-5;4];
интервал (-2;3);
луч [-10;+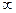 ); );
Несимметричным относительно нуля множеством является и промежуток [-2;2), так как –2 принадлежит этому множеству, а противоположное число 2 ему не принадлежит.
Определение:
Функция у = f(x) называется четной
, если:
1) область определения D(f) есть множество, симметричное относительно нуля;
2) для любого х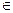 D(f) выполняется равенство D(f) выполняется равенство
f(-x) = f(x)
Таким образом, вопрос о четности или нечетности той или иной функции надо рассматривать, учитывая всякий раз не только вид аналитического выражения, но и тот промежуток, на котором определена данная функция. Ответ на вопрос: “Является ли, например, функция у = 1-х четной функцией?” зависит от выбора области определения. Если указанная функция определена на промежутке, симметричном относительно нуля. четной функцией?” зависит от выбора области определения. Если указанная функция определена на промежутке, симметричном относительно нуля.
Например, на всей числовой прямой, или на отрезке [-1;1], то в этих случаях функция у = 1-х является четной функцией. Если же предположим, что область определения есть отрезок [-1;2], то функция у = 1-х является четной функцией. Если же предположим, что область определения есть отрезок [-1;2], то функция у = 1-х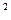 не является нечетной. не является нечетной.
Заметим, что наряду с четными и нечетными функциями есть функции, не являющиеся ни теми, ни другими, например, такими являются функции
у=1+sinx; у = 2 ; у = ; у = 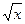 . .
Итак, при исследовании функции у = f(x) на четность или нечетность, необходимо поступать следующим образом:
а) выяснить симметричность области определения функции у = f(x) относительно нуля;
б) если область определения функции не симметрична относительно нуля, то функция не является ни четной, ни нечетной;
в) если область определения функции не симметрична относительно нуля, то необходимо проверить истинность равенств:
f(-x) = f(x) (1)
или f(-x) = f(x) (2) для всех х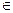 D(f) D(f)
Если выполняется равенство (1), то функция у = f(x) четная; если выполняется равенство (2), то функция у = f(x) нечетная. Если не выполняется ни одно из равенств (1) или (2), то функция не является ни четной, ни нечетной.
Можно предложить следующую блок-схему исследования функций на четность и нечетность:
_
 
+
  + +
_
+
Пример
:
исследовать на четность и нечетность функции:
1) у = 8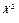 ; 2) у = ; 2) у =  ; 3) у = ; 3) у = 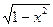 ; 4) у = ; 4) у =  . .
Областью определения функции у = 8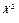 является числовая прямая (- является числовая прямая (-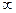 ; + ; +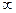 ) – симметричное относительно нуля множество. Далее, имеем f(x) = 8 ) – симметричное относительно нуля множество. Далее, имеем f(x) = 8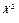 ; ;
f(-x) = 8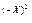 = 8 = 8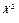 . Таким образом, f(-x) = f(x) , т.е. функция является чётной. . Таким образом, f(-x) = f(x) , т.е. функция является чётной.
2) Областью определения функции y =  является промежуток (0; + является промежуток (0; +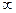 ) – не симметричное относительно нуля множество, поэтому функция y = ) – не симметричное относительно нуля множество, поэтому функция y =  не является ни чётной, ни нечётной. не является ни чётной, ни нечётной.
3) Область определения функции у = 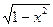 находится из условия находится из условия 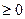 или (x – 1)(x + 1) или (x – 1)(x + 1)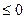 , таким образом, областью определения данной функции является отрезок [-1; 1] – симметричное относительно нуля множество. Далее, имеем , таким образом, областью определения данной функции является отрезок [-1; 1] – симметричное относительно нуля множество. Далее, имеем
f(x) = 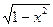 ; f(-x) = ; f(-x) =  = = 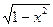 , т.е. функция у = , т.е. функция у = 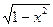 является чётной. является чётной.
4) Функция у =  не определена при тех значениях x, при которых знаменатель не определена при тех значениях x, при которых знаменатель 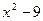 = 0, т.е. в таких точках –3 и3 значит, область определения функции D(f) = (- = 0, т.е. в таких точках –3 и3 значит, область определения функции D(f) = (-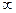 ; -3) ; -3) 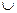 (-3; 3) (-3; 3) 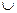 (3; + (3; +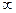 ) - симметричное относительно нуля множество. Далее f(x) = ) - симметричное относительно нуля множество. Далее f(x) =  ; f(x) = ; f(x) =  = - = - 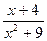 . .
Так как f(-x) f(x) и f(-x) f(x) и f(-x) -f(x), то функция не является ни чётной, ни нечётной. -f(x), то функция не является ни чётной, ни нечётной.
Рассмотрим основные свойства чётных и нечётных функций.
Свойство 1.
Если y = f(x) и y =  (x) – нечётные функции, то их алгебраическая сумма и разность есть функция нечётная. (x) – нечётные функции, то их алгебраическая сумма и разность есть функция нечётная.
Доказательство.
Пусть Функции y = (x) и y =  (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму и разность данных функций (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму и разность данных функций
 (x) и (x) и  (x) соответственно: (x) соответственно:
 (x) = f(x) + (x) = f(x) +  (x); (x);  = f(x) - = f(x) -  (x). (x).
Так как по определению f(-x) = -f(x) и  (-x) = - (-x) = - (x), то (x), то
 (-x) = f(-x) + (-x) = f(-x) +  (-x) = -f(x) - (-x) = -f(x) -  (x) = - (f(x) + (x) = - (f(x) +  (x)) = - (x)) = - (x) (x)
 (-x) = f(-x) - (-x) = f(-x) -  (-x) = -f(x) + (-x) = -f(x) +  (x) = - (f(x) - (x) = - (f(x) -  (x)) = - (x)) = - (x). (x).
Полученные равенства означают, что  (x) и (x) и  (x) – нечётные функции. (x) – нечётные функции.
Свойство 2.
Если y = f(x) и y =  (x) – нечётные функции, то их произведение и частное есть функция чётная. (x) – нечётные функции, то их произведение и частное есть функция чётная.
Доказательство
Пусть функции y = f(x) и y =  (x) имеют область определения X, симметричную относительно нуля. Обозначим произведение и частное данных функций Ф (x) имеют область определения X, симметричную относительно нуля. Обозначим произведение и частное данных функций Ф (x) и Ф (x) и Ф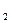 (x) соответственно: (x) соответственно:
Ф (x) = f(x) (x) = f(x)  (x); Ф (x); Ф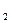 (x) = (x) = 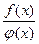 ( ( (x) (x)  0). 0).
Учитывая, что функции f(x) и  (x) – нечётные, будем иметь: (x) – нечётные, будем иметь:
Ф (-x) = f(-x) (-x) = f(-x)  (-x) = (-f(x)) (- (-x) = (-f(x)) (- (x)) = f(x) (x)) = f(x)  (x) = Ф (x) = Ф (x); (x);
Ф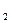 (-x) = (-x) = 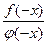 = =  = = 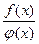 = Ф = Ф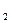 (x). (x).
Полученные равенства доказывают, что Ф (x) и Ф (x) и Ф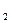 (x) функции чётные. (x) функции чётные.
Свойство 3.
Если y = f(x) и y =  (x) – чётные функции , то их сумма, разность, произведение и частное есть функция чётная. (x) – чётные функции , то их сумма, разность, произведение и частное есть функция чётная.
Пусть функции y = f(x) и y =  (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму данных функций G (x) имеют область определения X, симметричную относительно нуля. Обозначим сумму данных функций G (x), (x),
разность функций G (x), произведение функций G (x), произведение функций G (x), частное данных функций G (x), частное данных функций G (x) соответственно: (x) соответственно:
G (x) = f(x) + (x) = f(x) +  (x); G (x); G (x) = f(x) - (x) = f(x) -  (x); G (x); G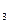 (x) = f(x) (x) = f(x)  (x); (x);
G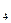 (x) = (x) = 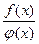 ( (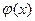  0). 0).
Докажем, что G (x), G (x), G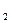 (x), G (x), G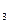 (x), G (x), G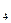 (x) – чётные функции. (x) – чётные функции.
Доказательство
Учитывая, что f(x) и  (x) – чётные функции будем иметь: (x) – чётные функции будем иметь:
G (-x) = f(-x) + (-x) = f(-x) +  (-x) = f(x) + (-x) = f(x) +  (x) = G (x) = G (x); (x);
G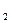 (-x) = f(-x) - (-x) = f(-x) -  (-x) = f(x) - (-x) = f(x) -  (x) = G (x) = G (x); (x);
G (-x) = f(-x) (-x) = f(-x)  (-x) = f(x) (-x) = f(x)  (x) = G (x) = G (x); (x);
G (-x) = (-x) =  = = 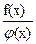 = G = G (x). (x).
Свойство 4.
Если y = f(x) – чётная функция, а y =  (x) – нечётная функция, то их произведение является нечётной функцией. (x) – нечётная функция, то их произведение является нечётной функцией.
Пусть функции y = f(x) и y =  (x) имеют область определения X, симметричную относительно нуля, причём по определению (x) имеют область определения X, симметричную относительно нуля, причём по определению
F(-x) = f(x),  (-x) = - (-x) = - (x). (x).
Обозначим произведение данных функций Q(x) = f(x)  (x). Докажем, что Q(x) функция нечётная. (x). Докажем, что Q(x) функция нечётная.
Доказательство
Учитывая, что f(x) – функция чётная, а  (x) – функция нечётная, будем иметь: (x) – функция нечётная, будем иметь:
Q(-x) = f(-x)  (-x) = f(x) (- (-x) = f(x) (- (x)) = -f(x) (x)) = -f(x)  (x) = -Q(x). (x) = -Q(x).
Полученное равенство означает, что функция Q(x) нечётная.
Свойство 5.
Всякую функцию, определённую на множестве X, симметричную относительно нуля, можно представить в виде суммы двух функций, каждая из которых определена на том же множестве X и одна из которых чётная, а другая нечётная.
Доказательство
Пусть функция y = f(x) имеет область определения X, симметричную относительно нуля.
Покажем, что существуют функции y =  (x) и y = (x) и y =  (x), каждая из которых определена на том же множестве X, и они такие, что (x), каждая из которых определена на том же множестве X, и они такие, что
y =  (x) + (x) +  (x) = f(x), где y = (x) = f(x), где y =  (x) – чётная функция, а y = (x) – чётная функция, а y =  (x) – нечётная функции. (x) – нечётная функции.
Положим  (x) = (x) = 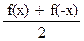 ; ;  (x) = (x) = 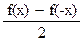 . .
Тогда ясно, что  (x) и (x) и  (x) определены на множестве X, так как f(x) определена на симметричном относительно нуля множестве X и (x) определены на множестве X, так как f(x) определена на симметричном относительно нуля множестве X и
 (-x) = (-x) = 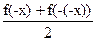 = = 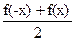 = =  (x); (x);
 (-x) = (-x) =  = =  = - = -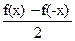 = - = - (x); (x);
 (x) + (x) +  (x) = (x) =  + + 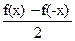 = = 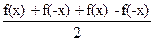 = = 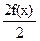 = =
= f(x), f(x),
что и требовалось доказать.
Пример.
Функцию y = 2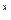 можно представить в виде суммы двух функций y = можно представить в виде суммы двух функций y =  (x), где (x), где  (x) = (x) =  , и y = , и y =  (x), где (x), где  (x) = (x) =  , причём функция y = , причём функция y =  (x) – чётная, а функция y = (x) – чётная, а функция y =  (x) – нечётная. (x) – нечётная.
Многие важные процессы в природе и технике являются периодическими, т.е. повторяющимися по истечении некоторого промежутка времени. Такие периодически повторяющиеся процессы описываются периодическими функциями. Поэтому особенно важно правильное понимание определения периодической функции.
Определение.
Функция y = f(x) называется периодической, если существует число   0 такое, что выполняются следующие два условия: 0 такое, что выполняются следующие два условия:
1) для любого x из области определения функции y = f(x) числа (x +  ) и (x – T) также входят в область определения и 2) для любого x из области определения выполняется равенство f(x + ) и (x – T) также входят в область определения и 2) для любого x из области определения выполняется равенство f(x +  ) = f(x). ) = f(x).
Число Т называют периодом функции y = f(x).
Замечание.
Для периодической функции имеет место равенство
f(x – T) = f(x). Действительно, функция y = f(x) в точке (x – T) определена и
f(x) = f[(x – T) + T] = f(x – T).
Покажем, что если число Т есть период функции y = f(x), то любое из чисел nT, где n 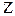 , n , n 0 является периодом этой функции. 0 является периодом этой функции.
Действительно, пусть n = 1, тогда согласно определению и замечанию:
а) точки (x + 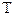 ) и (x – T) принадлежат области определения функции y = f(x); ) и (x – T) принадлежат области определения функции y = f(x);
б) f(x) = f(x + 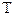 ) и f(x) = f(x – T). ) и f(x) = f(x – T).
Предположим, что для n = k справедливо утверждение точки (x + kT) и (x – kT) принадлежат области определения функции y = f(x). Докажем справедливость этого утверждения при n = k + 1.
По предположению точки (x + kT) и (x – kT) принадлежат области определения функции y = f(x) и Т есть её период. Следовательно, точки
[(x + kT) + T] и [(x – kT) – T], т.е. точки [x + (k + 1)T] и [x - (k + 1)T], принадлежат её области определения.
Итак, для любого x из области определения функции y = f(x) при любом n Z, n Z, n 0 точки (x + n 0 точки (x + n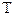 ) и (x – nT) принадлежат области её определения. ) и (x – nT) принадлежат области её определения.
Предположим, что для любого n = kсправедливо утверждение
f(x) = f(x + kT) и f(x) = f(x – kT). Докажем справедливость этого утверждения при n = k + 1. Действительно, так как Т является периодом функции y = f(x), то для точки (x + kT) имеем [(x + kT) + T] = f(x + kT), но по предположению
f(x) = f(x + kT) следовательно, f(x) = f[x + (k + 1)T].
Аналогично для точки (x – kT) доказывается, что f(x) = f[x - (k + 1)T], т.е. для любого целого отличного от нуля n утверждение f(x) = f(x + nT) и
f(x) = f(x - nT) доказано.
Число Т называется главным периодом
, если оно положительно и является наименьшим среди всех положительных периодов, т.е. из положительных периодов функции y = f(x) (если он существует) называют её основным (главным периодом).
Рассмотрим примеры.
Пример №1.
Функция y ={x} ({x} – дробная часть числа х) – периодическая. Заметим, что по определению 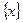 = х – [х], где [x] – целая часть числа х. Область определения данной функции - вся числовая прямая, поэтому для любого действительного числа х и любого T = х – [х], где [x] – целая часть числа х. Область определения данной функции - вся числовая прямая, поэтому для любого действительного числа х и любого T x, Т x, Т 0 числа (х + Т) и (х - Т) принадлежат области определения рассматриваемой функции и f(x +T ) = {x+T} = x + T – [x + T] = x + T –([x] + T) = x + T – [x] – T = x – [x] = {x}, где Т 0 числа (х + Т) и (х - Т) принадлежат области определения рассматриваемой функции и f(x +T ) = {x+T} = x + T – [x + T] = x + T –([x] + T) = x + T – [x] – T = x – [x] = {x}, где Т Z, T Z, T 0. 0.
Таким образом, функция у = {x} – периодическая с периодом Т, где Т Z, T Z, T 0. 0.
Наименьшее целое положительное число равно единице. Следовательно, основной период данной функции Т = 1.
Построим график функции у = {x}.
Для этого сначала построим график функции на промежутке х  [0;1), длина которого равна основному периоду функции. Если х [0;1), длина которого равна основному периоду функции. Если х  [0;1), то {x} = x, то есть на этом промежутке имеем у = х. [0;1), то {x} = x, то есть на этом промежутке имеем у = х.
Весь график функции у = {x} получим параллельным переносом графика функции у = {x}, где х [0;1) вдоль оси абсцисс на [0;1) вдоль оси абсцисс на 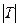 = 1. = 1.

Пример № 2
Функция Дирихле – периодическая с периодом T = r, где r = Q.Действительно,
D(x) = 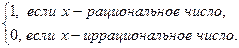
D(x + r) = 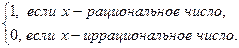
Так как r – рациональное число, то сумма х + r- рациональное число, как сумма двух рациональных чисел; с другой стороны, х + r- иррациональное число, как сума иррационального и рационального чисел.
Следовательно, D(x + r) = D(x).
Пример № 3
Функция y = sin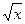 не является периодической, так как, например для числа не является периодической, так как, например для числа
х = 0 число (х – Т) при Т > 0 или число (х + Т) при Т < 0 не принадлежат области определения данной функции.
Пример № 4
Найти период функции
y = Asin (mx + 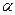 ), где А, m, ), где А, m, 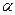 - постоянные величины, A - постоянные величины, A 0, m 0, m 0, 0,
x – аргумент.
Область определения функции – числовая прямая, поэтому числа (х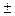 Т) Т) R, где Т R, где Т 0. Пусть основной период данной функции равен Т. Тогда для данной функции при любых действительных х рассмотрим равенство 0. Пусть основной период данной функции равен Т. Тогда для данной функции при любых действительных х рассмотрим равенство
A sin (m (x + T) + 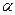 ) = A sin (mx + ) = A sin (mx + 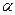 ). ).
Следовательно,
A (sin (m (x + T) + 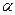 ) – sin (mx + ) – sin (mx + 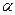 ) = 0. ) = 0.
Применяя формулу разности синусов, будем иметь:
2А sin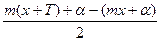 cos cos 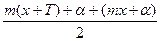 = 0 = 0
2А sin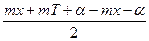 cos cos 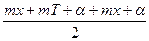 = 0 = 0
2А sin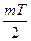 cos cos 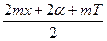 = 0 = 0
2А sin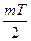 cos cos = 0 = 0
Это произведение должно равняться нулю независимо от значений х.
Так как х - переменная величина, то 2cos  0, А 0, А 0 по условию, тогда sin 0 по условию, тогда sin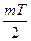 = 0, откуда следует = 0, откуда следует
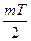 = =  , или , или 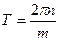 , где n , где n Z. Z.
Из множества значений Т наименьшее положительное значение получим при наименьшем положительном значении n = 1, значит период данной функции
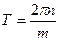 . .
Заметим, что период функции у = А sin (mx + 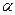 ) не зависит от A и ) не зависит от A и 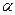 . .
Аналогично можно найти основные периоды и остальных тригонометрических функций.
Таким образом, функции
y = sinxи y = cosxимеют основной период Т = 2
у = tgxи у = ctgxимеют основной период Т =  , ,
а функции у = sin (mx + 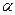 ) и у = cos(mx + ) и у = cos(mx + 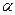 ) имеют основной период Т = ) имеют основной период Т =  . .
Функции у = tg (mx + 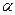 ) и у = ctg (mx + ) и у = ctg (mx + 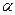 ) имеют основной период Т = ) имеют основной период Т = 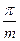 . .
 Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической. Отметим некоторые свойства периодических функций. Заметим, что сумма разность, произведение и частное двух периодических функций может быть функцией как периодической, так и не периодической.
Теорема 1.
Если периодические функции y = f1
(x) и y = f2
(x), xÎX, имеют один и тот же период T, то их сумма, разность, произведение тоже будут периодическими функциями и число Т будет их периодом.
Доказательство
Так как функция y = f1
(x) – периодическая с периодом Т ¹ 0, то для любого xÎX выполняется равенство
f1
(x +Т) = f1
(x) (1)
Так как функция y = f2
(x) – периодическая с периодом Т ¹ 0, то для любого xÎX выполняется равенство
f2
(x +Т) = f2
(x) (2)
Рассмотрим функцию z (x) = f1
(x) ±f2
(x), заданную на множестве X. Тогда для любого xÎX согласно равенствам (1) и (2) будем иметь
z (x +T) = f1
(x +T) ± f2
(x +Т) = f1
(x) ± f2
(x) = Z (x).
Последнее равенство доказывает периодичность функции z (x) представляющей собой сумму или разность двух периодических функций с одним и тем же периодом Т.
Рассмотрим функцию t (x) = f1
(x)×f2
(x), заданную на множестве Х. Тогда для любого xÎX согласно равенствам (1) и (2) будем иметь
t (x +T) = f1
(x +T) ×f2
(x +Т) = f1
(x) ×f2
(x) = t (x).
Данное равенство доказывает периодичность функции t(x) представляющей собой произведение двух периодических функций с одним и тем же периодом Т, причем число Т является периодом как функции t(x), так и функции z(x).
Замечание.
Если число Т было наименьшим положительным периодом (т.е. основным периодом) двух заданных функций, то после их сложения или умножения Т может перестать быть наименьшим из положительных периодов.
Пример 5.
Функция f1
(x) = 3 sinx + 2 имеет основной период 2p, функция f2
(x) = 2 – 3 sinx имеет основной период 2p, а их сумма
z (x ) = f1
(x) +f2
(x) = 3 sin x + 2 + 2 – 3 sin x = 4
наименьшего положительного периода не имеет, так как при любом действительном значении a¹ 0 z(x+a) = z(x), т.е. любое действительное число является периодом функции z(x), а наименьшего положительного среди действительных чисел нет.
Пример 6.
Функция j1
(x) = sinx +1 и j2
(x) = 1- sinx имеют наименьший положительный период 2p, а для произведения
t(x) = j1
(x) ×j2
(x) = (sin x +1)(1- sin x) = 1- sin2
x = cos2
x =
наименьшим положительным периодом есть число p .
Определение
Периоды функций Т1
и Т2
называются соизмеримыми
, если существуют такие целые отличные от нуля числа m и n, что m×T1
= n×Т2
.
Пример 7.
Выясним, являются ли соизмеримыми периоды Т1
=  и и
Т2
=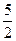
Решение. Данные периоды будут соизмеримыми, если уравнение  ×m = ×m = 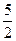 ×n имеет решение на множестве Z \ {0}. Умножим обе части данного уравнения на 6 (наименьшее общее кратное чисел 3 и 2), получим равносильное уравнение 4m = 15n, откуда m = 15k, n = 4k, где kÎZ \ {0}. Например, при k = 1 получим ×n имеет решение на множестве Z \ {0}. Умножим обе части данного уравнения на 6 (наименьшее общее кратное чисел 3 и 2), получим равносильное уравнение 4m = 15n, откуда m = 15k, n = 4k, где kÎZ \ {0}. Например, при k = 1 получим
 × 15 = × 15 = 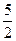 ×4 = 10 ×4 = 10
Ответ: Периоды Т1
и Т2
соизмеримы.
Теорема 2.
Если периодические функции y = f1
(x) и y = f2
(x), xÎX, имеют соизмеримые периоды Т1
и Т2
то они имеют общий период.
Доказательство.
Так как периоды Т2
и Т2
соизмеримы, то существуют целые отличные от нуля числа m и n такие, что m×T1
= n×T2
= T¹ 0. Следовательно, Т – общий период функций y = f1
(x) и y = f2
(x). Теорема доказана.
Замечание.
По теореме 1 число Т будет также периодом функций
z (x)= f1
(x) ± f2
(x), t(x) = f1
(x) f2
(x).
Пример 8.
Найти период функции
f(x) = sin2x + 3sin(3x-2) - 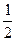 cos( cos(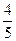 x +1). x +1).
Решение. Так как период синуса равен 2p, функция sin2x имеет период  = p функция sin(3x-2) = sin(3x-2 + 2p) = 3sin3(x- = p функция sin(3x-2) = sin(3x-2 + 2p) = 3sin3(x- + +  ) и ее период равен ) и ее период равен  . Аналогично, функция - . Аналогично, функция -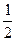 cos( cos(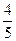 x +1) имеет период x +1) имеет период 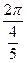 = = 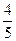 p. p.
Для того, чтобы найти общий период функции, представим периоды
Т1
= p; Т2
= p и Т3
= p и Т3
= 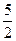 p в другом виде, а именно, коэффициенты при p в полученных периодах приведем к общему знаменателю, получим p в другом виде, а именно, коэффициенты при p в полученных периодах приведем к общему знаменателю, получим
Т1
=  p = 6× p = 6× ; Т2
= ; Т2
=  p = 4× p = 4× и Т3
= и Т3
=  p = p =  ×p и найдем наименьшее общее кратное числителей этих коэффициентов 6, 4 и 15. Оно равно 60. Следовательно, число Т = 60× ×p и найдем наименьшее общее кратное числителей этих коэффициентов 6, 4 и 15. Оно равно 60. Следовательно, число Т = 60× = 10p – основной период данной функции. = 10p – основной период данной функции.
Пример 9.
Найти период функции y = cos5x-sin2x.
Решение. Функция y = cos5x имеет период T1
= 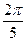 ; функция y = sin2x – период Т2
= ; функция y = sin2x – период Т2
=  = p. Представим периоды Т1
и Т2
в другом виде: Т1
= 2× = p. Представим периоды Т1
и Т2
в другом виде: Т1
= 2×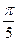 ; Т2
= 5× ; Т2
= 5×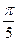 . Таким образом видно, что периоды Т1
и Т2
соизмеримы: 5Т1
= 2Т2
, откуда 5× . Таким образом видно, что периоды Т1
и Т2
соизмеримы: 5Т1
= 2Т2
, откуда 5×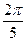 = 2×p = 2p. Следовательно, число 2p является периодом данной функции. = 2×p = 2p. Следовательно, число 2p является периодом данной функции.
Пример 10.
Найти основной период функции y = sin2
x.
Решение. Понизим степень функции y = sin2
x. Тогда y =  = =
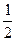 - -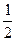 cos2x. Период этой функции равен периоду cos2x cos2x. Период этой функции равен периоду cos2x = p. Таким образом основной период данной функции равен p. = p. Таким образом основной период данной функции равен p.
Замечание.
Если Т1
и Т2
– основные периоды функций f1
(x) и f2
(x), то наименьшее положительное число Т, удовлетворяющее условиям:
Т = mT1
= nT2
, где m, nÎZ \ {0}, не обязательно является основным периодом функций f1
(x) ±f2
(x) и f1
(x) ×f2
(x).
Например, основные периоды функций y = cos2x + sinx и y = -sinx равны 2p, а основной период их суммы y = cos2x равен p.
Или, вернемся к примеру 6 и посмотрим на функцию y = sin2
x как на произведение функций y = sinx×sinx. Основной период функции y = sinx есть число 2p, но решая пример 6, мы показали, что основной период функции
y = sin2
x равен p.
Заметим, что сложная функция, промежуточным аргументом которой служит периодическая функция, есть функция периодическая, причем периоды этих функций совпадают. Докажем
Теорему 3.
Если y = f(j(x)) – сложная функция, где j(x) – периодическая функция с периодом Т, то и сложная функция периодическая с периодом Т.
Доказательство.
Так как j(x) – периодическая функция с периодом Т, то для любого действительного xиз области определения функции j(x) имеем
j(x + Т) = j(x),
тогда для функции y = f(j(x)) при любом действительном х из области определения функции j(x) будем иметь
j(x + Т) = f (j(x)) = f(j(x)) = y(x).
Последнее равенство доказывает, что функция y = f(j(x)) периодическая с периодом Т.
Пример 11.
Функция y = cos3x периодическая с периодом  = p. В силу теоремы 3 функция y = 5cos2
2x + = p. В силу теоремы 3 функция y = 5cos2
2x + 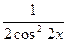 +3 периодическая с периодом p. +3 периодическая с периодом p.
Рассмотрим примеры на доказательство периодичности или не периодичности функций.
Пример 12.
Доказать, что функция y = sin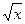 не является периодической. не является периодической.
Доказательство.
I способ: D(y) = [0;+¥). Пусть положительное число
Т – период данной функции, тогда должно выполнятся условие (х-Т) ÎD(y), для любого xÎD(y). Но при x = 0 (х-Т) ÏD(y), следовательно, T > 0 не является периодом функции.
Докажем, что Т < 0 не может быть периодом функции y = sin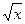 . .
Если T < 0 – период данной функции, то должно выполнятся условие (х + Т) ÎD(y) для любого xÎD(y). Но при x = 0 (х + Т) ÏD(y), следовательно, T < 0 не является периодом функции.
II способ: Предположим, что функция y = sin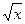 имеет период, равный Т. Тогда y = sin имеет период, равный Т. Тогда y = sin = y = sin = y = sin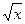 при любом действительном xÎD(y). При x = 0 будем иметь, что sin при любом действительном xÎD(y). При x = 0 будем иметь, что sin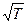 = sin 0 = 0. Значит = sin 0 = 0. Значит
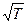 = pn, (1) = pn, (1)
а при x = T получим sin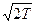 = sin = sin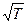 = 0. Следовательно, = 0. Следовательно,
sin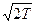 = pk. (2) = pk. (2)
Разделив почленно (2) на (1) при n¹ 0, получим 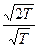 = = 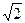 = = , чего не может быть, так как , чего не может быть, так как 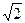 число иррациональное. число иррациональное.
Пример 13.
Доказать, что функция y = cos2
x не является периодической.
Доказательство.
Пусть данная функция имеет период Т ¹ 0. Тогда для любого xÎD(y) (D(y) = R) должно выполнятся равенство
cos (x+T)2
= cos x2
или
cos (x+T)2
- cosx2
= 0
Преобразуем данное равенство по формуле разности косинусов, получим
2 sin  × sin × sin 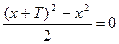
2sin (x2
+ T×x +  ) × sin (T×x + ) × sin (T×x +  ) = o ) = o
Это произведение должно равняться нулю независимо от значений переменной величины x, а это невозможно, sin (T×x +  ) ¹o и ) ¹o и
sin(x2
+ T×x +  ) ¹ 0. Значит допущение, что функция y = cos2
x периодическая неверно, т.е. данная функция не является периодической. ) ¹ 0. Значит допущение, что функция y = cos2
x периодическая неверно, т.е. данная функция не является периодической.
Пример 14.
Доказать, что функция y = |sin (x)| является периодической с периодом p.
Доказательство.
D(y) = R. Пусть периодом данной функции будет число Т ¹ 0. Тогда
|sin (x + Т)| = |sin (x)| (3)
Это равенство будет выполнятся в двух случаях:
1) sin (x + Т) = sin (x) и тогда
sin (x + Т)-sin (x) = 0
2 cos (x +  )×sin )×sin  = 0. = 0.
Это произведение должно равняться нулю независимо от переменной x, а это возможно только при sin = 0. Откуда = 0. Откуда
 = pk и Т = 2pk, что приводит к основному периоду 2p. = pk и Т = 2pk, что приводит к основному периоду 2p.
2) sin (x + Т) = -sin (x). (4)
Тогда sin (x + Т) +sin (x) = 0 и
2 sin (x +  )×cos )×cos = 0. = 0.
Откуда  = = 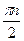 и Т = pn, что приводит к основному периоду Т = p. Так как при Т = p выполняется равенство (4), следовательно, и равенство (3). Значит, Т = p есть период функции y = |sin (x)|. и Т = pn, что приводит к основному периоду Т = p. Так как при Т = p выполняется равенство (4), следовательно, и равенство (3). Значит, Т = p есть период функции y = |sin (x)|.
§5 Тестовые контрольные работы по теме «Числовые функции. Сложная функция. Четные нечетные функции. Периодические функции»
Рассмотрим комплект тестовых заданий по теме «Числовые функции. Сложная функция. Четные нечетные функции. Периодические функции».
При разработке данного комплекта тестовых заданий учитывались следующие моменты:
1) содержание заданий, вопросов охватывает наиболее принципиальные стороны и идеи темы;
2) в задания сделан акцент не на проверку навыков, а на выявление глубины освоения идейного содержания темы, проявлению математической эрудиции;
3) по усмотрению учителя тестовое задание может предлагаться ученикам не полностью, а частями.
4) задания обеспечивают возможность проведения итоговых занятий на заключительном этапе изучения понятия функции в школьном курсе математики.
Комплект тестовых заданий составлен в четырех вариантах и включает двенадцать вопросов. На каждый из них дается четыре ответа для выбора правильного из них. Вопросы в заданиях предлагаются в текстовой и графической формах. Задания рассчитаны на 45 минут работы школьника.
Вариант
I
1. Какое равенство не задает функцию?
а) y2
= x2
; б) y = x2
; в) y = lgx; г) y = 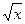 . .
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
 
 
3) Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x)) ?
а) f(x) = tg(x), g(x) = arctg x; б) f(x) =  , g(x) = x3
; , g(x) = x3
;
в) f(x) = x2
, g(x) = 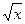 ; г) f(x) = ; г) f(x) = 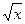 , g(x) = x2
. , g(x) = x2
.
4) Даны функции f(x) = x2
и g(x) = 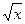 . Какая запись в таком случае верна? . Какая запись в таком случае верна?
а) f(g(x)) = (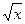 )2
; б) f(g(x)) = )2
; б) f(g(x)) = 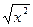 ; ;
в) f(g(x)) = |x|; г) f(g(x)) = x.
5) На каком из рисунков изображен график четной функции?
 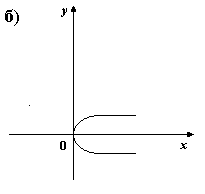
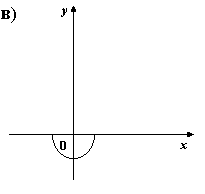 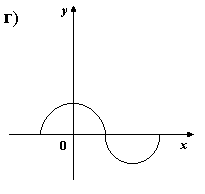
6. Укажите четную функцию.
а) y = sin (2x+1); б) y = sin (x2
+1);
в) y = cos (x2
+1); г) y = x+cosx.
7. Укажите нечетную функцию.
а) f(x) = x3
+1; б) f(x) = 2x
– 2-
x
;
в) f(x) = 2x
+ 2-
x
; г) f(x) = 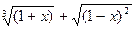
8. Какое высказывание ложно?
а) Сумма двух четных на R функций есть функция четная.
б) Разность двух четных на R функций есть функция четная.
в) Произведение двух четных на R функций есть функция четная.
г) Всякая функция есть функция четная, либо нечетная.
9. Какие из данных множеств могут быть областями определения периодических функций?
а) (-¥; +¥); б) (0;+¥); в) множество всех чисел, кроме чисел вида pk, где k = 0, ±1, ±2, …
10. Какая из функций обладает следующими свойствами:
существует такое t¹ 0, что при любом xиз области определения выполняется равенство f(x+t) = f(x)?
а) y = 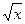 ; б) y = x2
; в) y = sin ; б) y = x2
; в) y = sin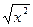 ; г) y = xsinx. ; г) y = xsinx.
11. Какая из функций не является периодической?
а) y = sin(x+1);
б) y = cos x + tg x;
в) y = x + sinx;
г) y = {x}.
12. Какая из функций имеет период  ? ?
а) y = tg x – ctg x; б) y = sin 2x;
в) y = cos 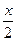 ; г) y = sin x + cos x. ; г) y = sin x + cos x.
Вариант
II
1. Какое равенство задает отношение, при котором каждому значению x соответствует не более одного значения y?
а) y2
= x2
; б) x2
y2
= 1; в) 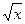 = x; г) siny = x. = x; г) siny = x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое нельзя рассматривать как график функции?
 
 
3. Для каких функций fи g равенство f(g(x)) = x верно не на всей области определения функции f(g(x))?
а) f(x) = sin x, g(x) = arcsin x; б) f(x) = arcsin x, g(x) = sin x;
в) f(x) = ex
, g(x) = lnx; г) f(x) = lnx, g(x) = ex
.
Даны функции f(x) =  и g(x) = x2
. Какая запись не верна? и g(x) = x2
. Какая запись не верна?
а) f(g(x)) = 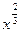 ; б)f(g(x)) = ; б)f(g(x)) = 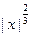 ; ;
в) f(g(x)) = 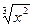 ; г) f(g(x)) = ( ; г) f(g(x)) = ( )2
; )2
;
4. На каком из рисунков изображен график четной функции?
 
 
5. Укажите четную функцию.
а) y = x2
– x; б) y = 2x
– 2-
x
;
в) 2x
+ 2-
x
; г) y = 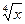 . .
6. Укажите нечетную функцию.
а) f(x) = cos x + sin x; б) f(x) = sin x + tg x;
в) f(x) = cos x + sin x; г) f(x) = tg x×ctg x.
7. Какое высказывание ложно?
а) Сумма двух нечетных функций на Rесть функция нечетная.
б) Разность двух нечетных функций на Rесть функция нечетная.
в) Произведение двух нечетных функций на R есть функция нечетная.
г) Произведение трех нечетных функций на Rесть функция нечетная.
8. Какие из данных множеств могут быть областями определения периодических функций?
а) R – множество действительных чисел;
б) (-2; +¥); в) R \ {2pk, kÎZ0
}.
9. Какая из функций обладает следующим свойством:
существует такое t¹ 0, что при любом xиз области определения верно равенство f (x+t) = f(x)?
а) y = x3
; б) y =  ; в) y = xcosx; г) y = sin ( ; в) y = xcosx; г) y = sin ( ). ).
10. Какая из функций не является периодической?
а) y = sin x + ctg x; б) y = cos (2x+1);
в) y = sin ( )2
; г) y = sin x×tg x. )2
; г) y = sin x×tg x.
11. У какой функции наименьший положительный период больше 2p?
а) y = sin x +  sin 2x + sin 2x +  sin 3x; sin 3x;
б) y = 3 tg 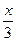 ; ;
в) y = tg x + ctg  ; ;
г) y = sin2
x.
Вариант
III
1. Какое равенство задает отношение, при котором некоторым значениям x соответствует более одного значения y?
а) y = arctgx; б) y = tgx; в) tgy = x; г) arctgy = x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое можно рассматривать как график функции?
 
 
3. Для каких функций f и gравенство f(g(x)) = x верно не на всей области опреднления функции f(g(x))?
4.
а) f(x) = 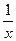 , g(x) = , g(x) = 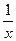 ; б) f(x) = 2x, g(x) = 0,5x; ; б) f(x) = 2x, g(x) = 0,5x;
в) f(x) = arccos x, g(x) = cos x; г) f(x) = cos x, g(x) = arccos x.
5. Для каких функций f и g имеет место равенство f(g(x)) = g(f(x))?
6.
а) f(x) =  , g(x) = x0
; б) f(x) = , g(x) = x0
; б) f(x) =  , g(x) = x4
; , g(x) = x4
;
в) f(x) =  , g(x) = x2
; г) f(x) = , g(x) = x2
; г) f(x) =  , g(x) = x3
. , g(x) = x3
.
7. На каком из рисунков изображен график четной функции?
 
 
8. Укажите четную функцию.
9.
а) y = sin x + tg x; б) y = sin x×tg x;
в) y = cos x×ctg x; г) y = tg x + ctg x.
10. Укажите, какая из приведенных функций нечетная?
11.
а) f(x) = 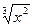 ; б) f(x) = lg ; б) f(x) = lg ; ;
в) f(x) = 10x
+ 10-
x
; г) f(x) = x5
– 1.
12. Пусть f – четная функция на R, а g – нечетная функция на R. Какое утверждение истинно?
а) f + g – функция четная; б) f – g – фуункция нечетная;
в) f×g – функция нечетная; г) 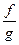 – функция четная. – функция четная.
13. Какие из данных множеств могут быть областями определения периодических функций?
а) Q – множество рациональных чисел;
б) (-¥; 0);
в) множество интервалов вида (2pk, p(2k+1)), где k = 0, ±1; ±2…
14. Какая из периодических функций не имеет наименьшего положительного периода?
а) y = sinx; б) y = {x}; в) y = 5;
г) y = tg (80x + 3).
15. Какая из функций не является периодической?
а) y = sin  ; б) y = tg x + sin 2x; ; б) y = tg x + sin 2x;
в) y = 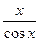 ; г) y = cos 4x. ; г) y = cos 4x.
16. Какие из следующих утверждений истинны?
а) Если число T – период функции f, то число 2T также период этой функции.
б) Если числа Т1
и Т2
– периоды функции f, то число (Т1
+Т2
) также период этой функции.
в) Если 2T – период функции f, то число T – также период этой функции.
г) Если T – период функции f, то число -T – также период этой функции.
Вариант
IV
1. Какое равенство задает отношение, которое не является функцией?
а) ln y = x; б) arcsin y = x; в) sin y = sin x; г) ey
= arcsin x.
2. На каком из рисунков изображено множество точек координатной плоскости, которое можно рассматривать как график функции?
 
 
3. Для каких функций f и g равенство f(g(x)) = x верно не на всей области определения функции f(g(x))?
а) f(x) = tg x, g(x) = arctg x; б) f(x) = arctg x, g(x) = tg x;
в) f(x) = 3x + 2, g(x) =  x - x - ; г) f(x) = - x, g(x) = - x. ; г) f(x) = - x, g(x) = - x.
4. Для каких функций f и g имеет место равенство f(g(x)) = g(f(x))?
а) f(x) =  , g(x) = , g(x) = 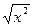 ; б) f(x) = 10x
, g(x) = lgx; ; б) f(x) = 10x
, g(x) = lgx;
в) f(x) = x2
, g(x) = x3
; г) f(x) = x4
, g(x) = 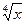
5. На каком из рисунков изображен график четной функции?
 
 
6. Укажите четную функцию.
7.
а) y = sin ( - x); б) y = 1 – sin x; - x); б) y = 1 – sin x;
в) y = cosx + x3
; в) y = (x + 4)2
8. Какая из приведенных функций нечетная?
а) f(x) = x sin x; б) f(x) = x + sin x;
в) f(x) = ctg2
x; г) f(x) = cos ( - x) + 2. - x) + 2.
9. На какой вопрос следует дать отрицательный ответ?
а) Может ли четная функция быть периодической?
б) Может ли периодическая функция иметь лишь один нуль?
в) Верно ли, что произведение двух функций различной четности есть функция нечетная?
10. Какие из данных множеств могут быть областями определения периодических функций?
а) N – множество натуральных чисел;
б) [-p; p];
в) множество всех чисел, кроме числа вида  (2k + 1), (2k + 1),
где k = 0; ±1; ±2, …
11. Какая из функций обладает следующим свойством: существует такое t¹ 0, что при любом x из области определения верно равенство
f(x) = f(x - t)?
а) y = 2 cos |x|; б) y = 3 + sin (2 +  ); );
в) y = 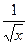 ; в) y = 2x
×cos x. ; в) y = 2x
×cos x.
12. Какая из функций не является периодической?
13.
а) y = |cos 2x|; б) y = sin x×cos  ; ;
в) y =  sin (6x + sin (6x +  ); г) y = 4 – cos ( ); г) y = 4 – cos ( + x). + x).
14. У какой функции наименьший положительный период меньше  ? ?
а) y = 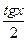 ; б) y = 3 cos ; б) y = 3 cos x; x;
в) y = 2 sin (6x +  ); г) y = -3 tg ( ); г) y = -3 tg ( - - 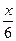 ). ).
Таблица кодов ответов
| Номер варианта |
Вопросы |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| Ответы |
| I |
а |
в |
г |
а |
в |
б |
б |
г |
а, в |
в |
в |
а |
| II |
в |
а |
б |
а |
в |
в |
б |
в |
а, в |
г |
в |
б |
| III |
в |
б |
в |
г |
б |
б |
б |
в |
а, в |
в |
б |
а, б, г |
| IV |
г |
г |
б |
в |
в |
а |
б |
б |
в |
а |
б |
в |
Заключение
Понятие функции является центральным в математическом образовании. От того, насколько полно и всесторонне школьник усвоит это понятие, зависит его дальнейшая адаптация в математической деятельности.
В школьном курсе математики учащиеся знакомятся с определением функции и той базы понятий, на котором оно основано, на протяжении всего периода обучения. При этом все содержание обучения построено так, что конечным результатом в идеале должно быть сформировано с одной стороны ясное и четкое представление об этом понятии, а с другой стороны близкое к современному пониманию функции как некоторого отображения произвольных множеств.
В данной работе сделана попытка, опираясь на основные школьные учебники, собрать материал по данной теме, систематизировать его для того, чтобы выделить важные моменты при формировании понятия функции и препятствовать формальному усвоению понятий, сопутствующих определению функции. Большую роль в достижении этой цели играют разработанные тестовые задания, разбор типичных примеров, в которых учащиеся зачастую дают неправильные ответы.
Данная работа охватывает весь материал, связанный с понятием функции в школьном курсе и может быть использована при работе на уроках в обычных, профильных классах и на факультативных занятиях по математике.
Литература
1. Ананченко К.О., Воробьев Н.Т., Петровский Г.Н. Алгебра. Учебник для 9 класса общеобразовательных школ с углубленным изучением математики. Минск: «Народная асвета», 1995.
2. Ананченко К.О., Коваленко В.С., Воробьев Н.Т. и др. Алгебра и начала анализа. Учебник для 10 класса с углубленным изучением математики общеобразовательной школы с русским языком обучения. Минск: «Народная асвета», 2000.
3. Вирченко Н.А., Ляшко И.И., Швецов К.И., Графики функций. Справочник. Киев: «Наукова думка», 1979.
4. Груденов Я.И. Изучение определений, аксиом, теорем. Пособие для учителей. М.: Прсвещение, 1981.
5. Кузнецова Е.П., Муравьева Л.Б., Шнеперман Л.Б., Ящин Б.Ю. Дидактические материалы по алгебре и началам анализа. 10 класс. Минск: «Народная асвета», 2000.
6. Майер Р.А. Из опыта изучения функций и пределов в старших классах. М.: Просвещение, 1981.
7. Майер Р.А. Задачи по формированию функциональных понятий.
8. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. Алгебра. Учебник для 7 класса общеобразовательных учреждений. М.: Просвещение, 1997.
9. Никольская И.А., Тараканова З.П. Задания для программированного опроса по алгебре и началам анализа. М.: Высшая школа, 1981.
10. Потапов М.К., Александров В.В., Пасиченко П.И. Изд. отдел УНЦ ДО МГУ, 1995.
11. Саранцев Г.И. Формирование математических понятий в средней школе // Матем. В школе. 1998. № 6. С.27.
12. Семенович А.Ф. Об определении понятия «отображение» // Матем. В школе. 2000. № 5. С.35.
13. Столяр А.А. Педагогика математики. Минск: « Вышейшая школа», 1986.
14. Фройденталь Г.Ф. Математика как педагогическая задача. В двух частях. М.: Прсвещение, 1983.
|