ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ОМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Авиа- и ракетостроение»
Специальность 160801- «Ракетостроение»
Расчетно-графическая работа
по дисциплине «Основы САПР»
Аппроксимация функций
Омск 2006
Введение
Цель работы:
Ознакомиться с методами интерполяции и аппроксимации функций
Задания:
Задание 1. Построить таблицу конечных разностей. Выполнить экстраполяцию на два узла от начала и от конца таблицы.
Задание 2. Построить интерполяционный многочлен Лагранжа и с его помощью найти
значения функции в узлах, соответствующих полушагу таблицы.
Задание 3. Найти значение f(x) с помощью формул Ньютона интерполирования вперед и назад.
Задание 4. Выполнить квадратичную сплайн-интерполяцию (по 6 узлам). Проконтролировать полученные оценки для промежуточных узлов.
Задание 5. Считая выбранную таблицу заданной для диапазона от 0 до 2, выполнить среднеквадратическую аппроксимацию тригонометрическим многочленом (отрезком ряда Фурье) третьей степени.
Исходные данные:
x=[11.0 11.1 11.2 11.3 11.4 11.5 11.6 11.7 11.8 11.9 12];
y=[-0.00023,1.080087,2.064282,2.854531,3.37121,3.560925,3.402017,2.90698,2.121544,1.120452,0.000357];
1. Построение массива конечных разностей. Выполнение экстраполяции
Массив конечных разностей рассчитываем по формуле:
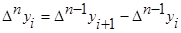 . .
for i=1:10
for j=1:11-i
y(i+1,j)=y(i,j+1)-y(i,j);
end
end
Результат расчёта:
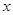 |
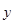 |
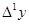 |
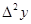 |
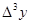 |
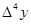 |
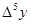 |
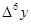 |
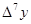 |
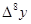 |
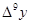 |
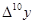 |
11,0
11,1
11,2
11,3
11,4
11,5
11,6
11,7
11,8
11,9
11,0
|
-0,0002
1,0801
2,0643
2.8545
3.3712
3.5609
3.4020
2.9070
2.1215
1.1205
0.0004
|
1.0803 0.9842 0.7902 0.5167 0.1897 -0.1589 -0.4950 -0.7854 -1.0011 -1.1201
-
|
-0.0961 -0.1939 -0.2736 -0.3270 -0.3486 -0.3361 -0.2904 -0.2157 -0.1190 -
-
|
-0.0978 -0.0796 -0.0534 -0.0217 0.0125 0.0457 0.0747 0.0967
-
-
-
|
0.0182 0.0262 0.0317 0.0342 0.0332 0.0290 0.0219
-
-
-
-
|
0.0080 0.0055 0.0024 -0.0009 -0.0042 -0.0071
-
-
-
-
-
|
-0.0025 -0.0031 -0.0033 -0.0033 -0.0029
-
-
-
-
-
-
|
-0.0006 -0.0002 0.0000 0.0004
-
-
-
-
-
-
-
|
0.0003 0.0003 0.0004
-
-
-
-
-
-
-
-
|
-0.0000 0.0001
-
-
-
-
-
-
-
-
-
|
0.0002
-
-
-
-
-
-
-
-
-
-
|
Экстраполяция на два узла от начала и конца таблицы с помощью многочлена Лагранжа.
n=11; % Степень многочлена
i=0;
for p=10.8:0.1:12.2
i=i+1;
x1(i)=p;
ff(i)=Lagrange(x,y,p,n);
end
for j=1:11
yy(j)=y(1,j);
end
subplot(2,1,1); plot(x,yy,'.-'); ylabel('y'); xlabel('x'); grid on; title('Первоначальные данные')
subplot(2,1,2); plot(x1,ff,'.-'); ylabel('y'); xlabel('x'); grid on; title('Экстраполяция')
Получим:
| х |
10.8 |
10.9 |
12.1 |
12.2 |
| f(х) |
-2,0234 |
-1,0701 |
-1,1291 |
-2,1535 |

Рис. 1. Экстраполяция на два узла многочленом Лагранжа
2. Нахождение значения приближенной функции с помощью многочлена Лагранжа
Запишем интерполяционный многочлен Лагранжа:
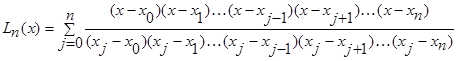 , ,
где х – произвольная координата на заданном интервале.
_____________________________________________________________
function [x]=Lagrange(x,y,a,n)
for i=1:n
for j=1:n
s(i,j)=1;
end
end
ss=1;
for j=1:n
for i=1:n
if j~=i
s(j,i)=(a-x(i))/(x(j)-x(i));
end
end
end
ss=prod(s,2);
L=0;
for k=1:n
L=L+y(1,k)*ss(k);
end
x=L;
_____________________________________________________________
i=0;
for p=11:0.01:12
i=i+1;
x1(i)=p;
ff(i)=Lagrange(x,y,x1(i),n);
end
subplot(2,1,2); plot(x1,ff,'.-'); ylabel('y'); xlabel('x'); grid on; title('ИнтерполяциямногочленомЛагранжа')

Рис. 2. Интерполяция многочленом Лагранжа
3. Определение значения функции с помощью формул Ньютона
а) Интерполяционная формула Ньютона для интерполирования вперёд:
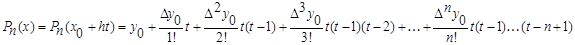
где 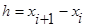 - промежуток между последовательными узлами интерполирования, (в рассматриваемом случае промежуток постоянен); - промежуток между последовательными узлами интерполирования, (в рассматриваемом случае промежуток постоянен);
n– степень многочлена;
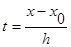 . .
_____________________________________________________________
function [x]=Nuton_vp(k,x,y,n);
n=round(k)+1; % Степень многочлена
if n==12
n=11;
end
t=(k-1)/1;
t1(1)=1;
for j=2:n
t1(j)=t-(j-2);
end
t2=cumprod(t1);
for j=1:n
Pn(j)=y(j,1)*t2(j)/FACTORIAL(j-1);
end
x=sum(Pn,2);
_____________________________________________________________
n=11;
i=0;
for p=11:0.05:12
i=i+1;
a=0.5+i*0.5;
x1(i)=p;
ff(i)=Nuton_vp(a,x,y,n);
end
% Построениеграфика
subplot(2,1,2); plot(x1,ff,'.-'); ylabel('y'); xlabel('x'); grid on
title('Интерполяция многочленом Ньютона вперёд')

Рис. 3. Интерполяция многочленом Ньютона вперёд
б) Формула Ньютона для интерполяции назад:
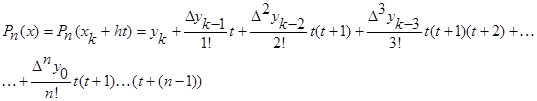
_____________________________________________________________
function [x]=Pnz(k,x,y);
n=12-round(k)+1; % Степень многочлена
ifn==12
n=11;
end
t=(k-11)/1;
t1(1)=1;
for i=2:n
t1(i)=t+(i-2);
end
t2=cumprod(t1);
for i=1:n
Pn(i)=y(i,12-i)*t2(i)/FACTORIAL(i-1);
end
x=sum(Pn,2);
_____________________________________________________________
i=0;
for p=11:0.05:12
i=i+1;
a=0.5+i*0.5;
x1(i)=p;
ff(i)=Nuton_nz(a,x,y);
end
% Построениеграфика
subplot(2,1,2); plot(x1,ff,'.-'); ylabel('y'); xlabel('x'); grid on
title('Интерполяция многочленом Ньютона назад')

Рис. 4. Интерполяция многочленом Ньютона назад
4. Квадратичная сплайн-интерполяция
Для того, чтобы выполнить квадратичную сплайн-интерполяцию по 6-ти узлам, необходимо задаться пятью уравнениями.
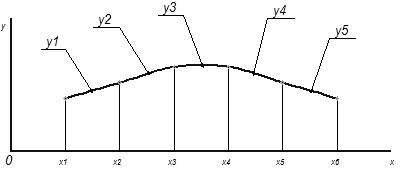
Рис. 5. К выводу коэффициентов при сплайн-интерполяции
При квадратичном сплайне уравнения будут иметь вид:
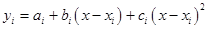 , ,  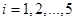 . .
На эти уравнения наложены следующие граничные условия:
 , , 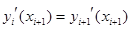 , , 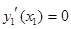 , , 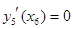 . .
Вычислим производную
 : : 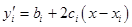 , ,  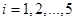 . (1) . (1)
Определим  при при 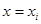 : : 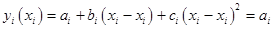 , , 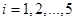 . (2) . (2)
В рассматриваемом примере 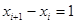 . С учетом этого, а также с учетом выражения (2) и условия . С учетом этого, а также с учетом выражения (2) и условия  , запишем следующую зависимость: , запишем следующую зависимость:
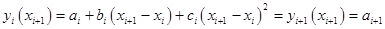 , , 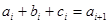 . .
Из условия 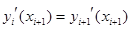 и выражения (1) получим: и выражения (1) получим: 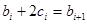 . .
Составим систему уравнений:
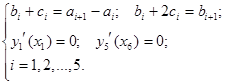
Решая эту систему, получим следующие зависимости для вычисления коэффициентов:
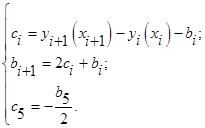
_____________________________________________________________
function [k]=Spl(aa,n,x,y);
c(1)=0;
b(1)=10*y(1,2)-10*y(1,1)-0.1*c(1);
for k=1:n-2
b(k+1)=0.2*c(k)+b(k);
c(k+1)=100*y(1,k+2)-100*y(1,k+1)-10*b(k+1);
end
j=floor(10*aa-109);
if j==6
j=5;
end
k=y(1,j)+b(j)*(aa-x(j))+c(j)*(aa-x(j))^2;
_____________________________________________________________
n=6;
clear yy; clear ff; clear x1; clear x1
for i=1:11
a=10.95+i*0.05;
ff(i)=Spline(a,n,x,y);
x3(i)=10.95+0.05*i;
end
for j=1:6
yy(j)=y(1,j);
x1(j)=x(j);
end
% Построение графика
subplot(2,1,1); plot(x1,yy,'o-'); ylabel('y'); xlabel('x'); grid on
title('Первоначальные данные')
subplot(2,1,2); plot(x3,ff,'.-');ylabel('y'); xlabel('x'); grid on
title('Интерполяция сплайнами')

Рис. 6. Интерполяция квадратичным сплайном
5. Среднеквадратичная аппроксимация тригонометрическим многочленом третьей степени
Тригонометрический многочлен ищется в виде:
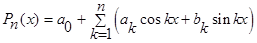 . .
Коэффициенты вычисляются по следующим формулам:
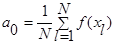 , , 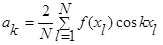 , , 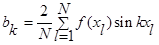 , ,  . .
где n– степень многочлена (в данном случае принимается n=3);
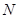 - число узловых точек. - число узловых точек.
_____________________________________________________________
function [x]=Furie(aa,x,y);
for i=1:11
xpi(i)=i*2*pi/11;
a=(aa-10.9)*10*2*pi/11;
end
n=3;
a0=sum(y,2)/11;
for i=1:3
for j=1:11
ak(i,j)=y(1,j)*cos(i*xpi(j));
bk(i,j)=y(1,j)*sin(i*xpi(j));
end
end
aksum=2*sum(ak,2)/11;
bksum=2*sum(bk,2)/11;
Tna=a0(1)+aksum(1)*cos(a)+bksum(1)*sin(a)+aksum(2)*cos(2*a)+bksum(2)*sin(2*a)+aksum(3)*cos(3*a)+bksum(3)*sin(3*a);
x=Tna;
_____________________________________________________________
for i=1:100
k(i)=10.99+i*0.01;
ff(i)=Furie(k(i),x,y);
end
for j=1:11
yy(j)=y(1,j);
end
subplot(2,1,2);
plot(x,yy,'o-',k,ff,'.-');ylabel('y');xlabel('x');grid on;
title('Аппроксимация тригонометрическим многочленом');

Рис. 7. Аппроксимация тригонометрическим многочленом
Список использованных источников
1. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989.
2. Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Физматгиз, 1966.
3. Калиткин Н.Н. Численные методы. М.: Наука, 1978.
4. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа. М.: Наука, 1967.
5. Бахвалов Н.С. Численные методы. М.: Наука, 1987.
6. Марчук Г.И. Методы вычислительной математики. М.: Наука, 1989.
7. Волков Е.А. Численные методы. М.: Наука, 1987.
|