Курсовая работа: Анализ методов сортировки одномерного массива
|
Название: Анализ методов сортировки одномерного массива Раздел: Рефераты по информатике Тип: курсовая работа | |
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫХЕРСОНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ Кафедра ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ рАЗРАБОТКА ПРОГРАММЫ ДЛЯ Анализа методов сортировки одномерных массивов. Курсовой проектпо дисциплине «Программирование» Пояснительная записка Исполнитель студент группы 2КСС3 ________________________ (подпись, дата) Руководитель старший преподаватель ________________________ (подпись, дата) Нормоконтролер старший преподаватель_________________________ (подпись, дата) РЕФЕРАТ Курсовой проект содержит: стр. – 39 машинописного текста, литературных источников – 5, приложения – 2 . Ключевые слова: ФУНКЦИЯ, ФАЙЛ, МЕТОД , МАССИВ . В курсовом проекте рассмотрена модификация и сравнения двух текстовых файлов. Программа написана на языке программирования Cи и работоспособна на IBM совместимых компьютерах. Программа имеет псевдографический и графический интерфейсы, обладает достаточным быстродействием и небольшим размером. СОДЕРЖАНИЕ Введение .................................................................................................... 31. Постановка задачи................................................................................ 5 1.1. Анализ существующих решений поставленной задачи................ 5 1.2. Обоснование выбора метода решения задачи............................... 16 2. Разработка алгоритма решения задачи............................................... 17 3. Разработка программы........................................................................ 18 3.1 Описание программы и используемых в ней функций ................... 18 3.1.1 Описание функции main()............................................................... 21 3.1.2 Описание функции srecmg()............................................................ 21 3.1.3 Описание функций qqsort()............................................................. 22 3.1.4 Описание функции grafix().............................................................. 23 3.2 Руководство программиста .............................................................. 25 3.3 Руководство оператора .................................................................... 26 Заключение................................................................................................. 28 Список использованной литературы........................................................ 29 Приложение 1 ........................................................................................... 30 Приложение 2 ........................................................................................... 39 ВВЕДЕНИЕ Си – это язык программирования общего назначения, хорошо известный своей эффективностью, экономичностью, и переносимостью. Указанные преимущества Си обеспечивают хорошее качество разработки почти любого вида программного продукта. Использование Си в качестве инструментального языка позволяет получать достаточно быстрые и компактные программы. Во многих случаях программы, написанные на Си, сравнимы по скорости с программами, написанными на языке ассемблера[2]. При этом они имеют лучшую наглядность. Си сочетает эффективность и мощность в относительно малом по размеру языке. Хотя Си не содержит встроенных компонент языка, выполняющих ввод-вывод, распределение памяти, манипуляций с экраном или управление процессами, тем не менее, системное окружение Си располагает библиотекой объектных модулей[3], в которой реализованы подобные функции. Библиотека[4] поддерживает многие из функций, которые требуются.[1] Язык Си – это универсальный язык программирования, для которого характерны экономичность выражения, современный поток управления и структуры данных, богатый набор операторов. Язык Си не является ни языком "очень высокого уровня", ни "большим" языком, и не предназначается для некоторой специальной области применения, но отсутствие ограничений и общность языка делают его более удобным и эффективным для многих задач, чем языки, предположительно более мощные. Он тесно связан с операционной системой "UNIX"[4] , так как был развит на этой системе и так как "UNIX" и ее программное обеспечение написано на "C". Сам язык, однако, не связан с какой–либо одной операционной системой или машиной; и хотя его называют языком системного программирования, так как он удобен для написания операционных систем, он с равным успехом использовался при написании больших вычислительных программ, программ для обработки текстов и баз данных [2]. 2. ПОСТАНОВКА ЗАДАЧИ 2.1 АНАЛИЗ СУЩЕСТВУЮЩИХ РЕШЕНИЙ ПОСТАВЛЕННОЙ ЗАДАЧИ В настоящее время существует множество алгоритмов cортировки[5] массивов, которые применяются в зависимости от того какие условия функционирования стоят перед разрабатымаемой программой. 1. Методы вставки. Алгоритм простых вставок. 1.1. Бинарные вставки 1.2. Двухпутевые вставки 1.3. Вставки одновременно нескольких элементов. 1.4. Вставки с убывающим шагом (метод Шелла) 1.5. Вставки в связанный список 1.6. Вставки в несколько связанных списков 2. Обменная сортировка 2.1. Метод пузырька 2.2. Модификация метода пузырька 2.3. Быстрая сортировка. 2.4. Обменная поразрядная сортировка 2.5. Параллельная сортировка Бэтчера 3. Сортировка посредством выбора ( Использование связанного списка для хранения информации о промежуточных максимумах.) 4. Сортировка посредством слияния Методы вставки. Алгоритм простых вставок. Ниже описан основной алгоритм простых вставок, который порождает несколько модификаций, используемых в заданиях. Алгоритм использует прием, которым пользуются игроки в карты при сортировке только что розданной колоды: очередная карта вставляется между уже упорядоченными ранее. Описание алгоритма простых вставок. Файл, подлежащий сортировке, в общем случае состоит из элементов-записей, включающих информационную часть и ключи, по которым производится упорядочение по возрастанию. Поскольку информационная часть почти не влияет на процесс сорировки, будем предполагать, что файлы, используемые в примерах, состот только из элементов-ключей, а информационная часть записи от сутствует. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ+ b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Бинарные вставки Для ускорения числа сравнений при поиске места, в которое нужно вставить элемент X, можно использовать логарифмический [5] поиск. Это означает, что сначала Х сравнивается с элементом k[j/2], затем, в зависимости от результата сравнения, с элементом, лежащим посередине между 1 и j/2 или посередине между j/2+1 и j и т.д. . При этом числосравнений для каждого j равно примерно log(j). Число пересылок эле ментов при этом не изменяется и остается примерно равным NЅ/4. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N + c*N*logN где a,b,c - неизвестные константы, зависящие от программной реализации алгоритма. Двухпутевые вставки Число пересылок можно сократить примерно в 2 раза до NЅ/8, если допустить сдвиги элементов не только вправо, но и влево. Для выходного файла резервируется место в памяти, равное 2N+1 ,где N - число элементов в исходном файле. Первый элемент пересылается в середину выходного файла. В дальнейшем элементы выходного файла сдвигаются вправо или влево в зависимости от того, в какую сторону нужно сдвигать меньше элементов. Присоединение новых элементов к выходному файлу происходит как справа, так и слева от центрального элемента с возможным сдвигом вправо или влево. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Вставки одновременно нескольких элементов. Модификация метода простых вставок заключается в том, что вместо одной переменной Х можно использовать несколько переменных Х1, Х2, ... Xm, которые имеют значения элементов, подлежащих вставке в уже упорядоченную часть файла. Х1, X2, ... Xm упорядочены по возрастанию, поэтому сравнивая Xm в цикле по переменной i с элементами упорядоченной части, мы можем гарантировать, что, если очередной элемент k[i] больше Xm, то он больше и остальных элементов. Перенос элементов исходного файла вперед в цикле по i выполняется на m элементов, то есть вместо k[i+1]=k[i] в исходном алгоритме в модифицированном алгоритме записывается k[i+m]=k[i]. При нахождении k[i] такого, что он меньше Хm, Хm ставится на место k[i+m] и m уменьшается на 1. Далее цикл по i продол-жается с новым m. Экономия числа переносов элементов достигается за счет переносов сразу на m элементов. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N + c*N*logN где a,b,c - неизвестные константы, зависящие от программной реализации алгоритма. Вставки с убывающим шагом (метод Шелла) Идея алгоритма состоит в обмене элементов, расположенных не только рядом, как в алгоритме простых вставок (п.1), но и далеко друг от друга, что значительно сокращает общее число операций перемещения элементов. Для примера возьмем файл из 16 элементов. Сначала просматриваются пары с шагом 8. Это пары элементов 1-9, 2-10, 3-11, 4-12, 5-13, 6-14, 7-15, 8-16. Если значения элементов в паре не упорядочены по возрастанию, то элементы меняются местами. Назовем этот этап 8-сортировкой. Следующий этап - 4-сортировка, на котором элементы в файле делятся на четверки: 1-5-9-13, 2-6-10-14, 3-7-11-15,4-8-12-16. Выполняется сортировка в каждой четверке. Сортировка может выполняться методом простых вставок (п.1). Следующий этап - 2-сортировка, когда элементы в файле делятся на 2 группы по 8: 1-3-5-7-9-11-13-15 и 2-4-6-8-10-12-14-16. Выполняется сортировка в каждой восьмерке. Наконец весь файл упорядочивается методом простых вставок. Поскольку дальние элементы уже переместились на свое место или находятся вблизи от него, этот этап будет значительно менее трудоемким, чем при сор-тировке вставками без предварительных "дальних" обменов. Файл после окончательной сортировки (1-сортировки): 61 87 154 170 275 426 503 509 512 612 653 677 703 765 897 908 Время работы алгоритма t примерно оценивается формулой: t=a*N**b где a и b - неизвестные константы, зависящие от программной реализа- ции алгоритма. Вставки в связанный список Среди общих способов улучшения алгоритма простых вставок можно рассмотреть способ, основанный на изменении структуры данных. Сортировка простыми вставками состоит из двух основных операций: - просмотра исходного файла со сравнением переменной Х с элементами K[i] файла; - вставки нового элемента путем сдвига оставшихся элементов вправо. Файл до сих пор рассматривался как линейный список и для выполнения операции вставки в нем необходимо переместить в среднем половину эле-ментов . Известно, что для операций вставки идеально подходитсвязанный список, так как в этом случае вставка требует всего лишь изменения нескольких связей. Операция последовательного просмотра для связанного списка почти так же проста, как и для линейного списка. Поскольку файл всегда просматривается в одном направлении, то достаточно иметь список только с одной связью. С другой стороны связанное распределение делает невозможным бинарный поиск, поэтому приобретая преимущество в выполнении операции вставки, мы теряем по сравнению с бинарным поиском в эффективности операции просмотра и сравнения. Рассмотрим алгоритм простых вставок на связанном вперед списке. Дан файл в виде связанныого списка, каждый элемент которого содержит кроме ключа K[i] еще и указатель на следующий элемент L[i]. Кроме того есть еще дополнительная переменная L[0], содержащая указатель на последний N-й элемент файла. Указатель L[N] равен нулю, что является признаком конца списка элементов. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Вставки в несколько связанных списков Идея метода основывается на предположении, что ключи в исходном файле имеют значения в некотором известном диапазоне MAX и в этом диапазоне они распределены довольно равномерно. Тогда по аналогии с методом вставки в один связанный список можно организовать несколько, например, Q списков. Величина Q зависит от ожидаемого среднего количес-тва элементов M в каждом списке то есть Q=N/M, N - количество ключей. При разработке программы нужно проанализировать зависимость времени работы метода от параметра М для различных исходных файлов и дать рекомендации по выбору оптимального значения. Схема алгоритма имеет следующий вид. Через Q обозначено количество списков, массив B[1]...B[Q] служит для хранения указателей на начала отдельных списков. Перед началом работы алгоритма элементы массива В предполагаются равными 0. Каждый i-й элемент исходного файла содержит ключ K[i] и указатель L[i] на следующий элемент списка. Значение L[i]=0 соответствует последнему элементу в списке, указатель B[1] указывает на начало первого подсписка и одновременно на начало всего списка. Через minK обозначено минимальное значение ключа в файле, через М - среднее выбранное значение количества элементов в подсписке. в - номер текущего списка, в который должен быть вставлен элемент K[j]. Величина R=MAX/Q есть диапазон значений ключей, приходящийся на один список. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Обменная сортировка Название этой группы методов произошло от основного типа операций, используемого в алгоритмах - обмен двух элементов в файле своими значениями. Эта операция используется и в других группах, поэтому классификацию нельзя признать вполне строгой, но данное разделение тем не менее является традиционным. Файл, подлежащий сортировке, в общем случае состоит из элементов-записей, включающих информационную часть и ключи, по которым производится упорядочение по возрастанию. Поскольку информационная часть почти не влияет на процесс сортировки, будем предполагать, что файлы, используемые в примерах, состот только из элементов-ключей, а информационная часть записи отсутствует. Метод пузырька Алгоритм довольно очевиден. Пары стоящих рядом элементов просматриваются в направлении снизу вверх и сравниваются. Если верхний элемент оказывается меньше нижнего, то они меняются местами. Продолжая этот процесс циклически, мы в конце концов придем к отсортированному файлу.Файл расположен вертикально снизу вверх, чтобы эффект всплывающего пузырька выглядел более наглядно. Элементы с большим значением ключа "всплывают" наверх, после последовательных сравнивнений с соседними элементами. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N где a,b - неизвестные константы, зависящие от программной реализа- ции алгоритма. Модификация метода пузырька Модификация метода пузырька состоит в том, что файл можно просматривать как с начала до конца, так и с конца до начала попеременно. Это несколько сокращает число перемещений элементов. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Быстрая сортировка. Основная стратегия ускорения алгоритмов сортировка - обмены между как можно более дальними элементами исходного файла - в методе быстрой сортировки реализована за счет того, что один из ключей в исходном файле используется для разделения его на два подфайла так, чтобы слева от выбранного элемента находились только элементы с меньшими ключами,а справа - только с большими. Элемент, разделяющий файл, помещается между его двумя подфайлами и процедура выполняется рекурсивно для каждой половины до тех пор, пока в очередном новом подфайле не окажется меньше, чем М элементов, где М - заранее выбранное число. Сортировка подфайлов, содержащих меньше чем М элементов, выполняется каким-либо простым методом, например простыми вставками. Таким образом, реализация метода зависит от двух параметров: значения М и способа выбора элемента, который предназначен для разделения файла на две части. Блок выбора Х в простейшем случае формулируется как X=K[l], однако это может привести к крайне неэффективному алгоритму. Наиболее простое лучшее решение - выбирать Х как случайный ключ из диапазона K[l] ... K[r] и обменять его с K[l]. Время работы алгоритма t примерно оценивается формулой: t=a*N*logN + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Обменная поразрядная сортировка Данный метод использует двоичное представление ключей. Файл сортируется последовательно по битам двоичного представления ключей,начиная со старшего. Ключи, имеющие значение данного бита, равноенулю, ставятся в левую половину файла, а ключи со значением бита 1 в правую. Функция b(ключ) возвращает значение ьита с номером b аргумента, m -максимальное количество значащих битов в ключах. Время работы алгоритма t примерно оценивается формулой:t=a*N*logN + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Параллельная сортировка Бэтчера Для получения алгоритма обменной сортировки, время работы которого меньше, чем NЅ, необходимо выбирать для сравнения и обмена ключи,расположенные возможно дальше друг от друга. Эта идея уже была реализована в алгоритме сортировки Шелла вставок с убывающим шагом, однако в данном алгоритме сравнения выполняются по-другому. Время работы алгоритма t примерно оценивается формулой:t=a*N*(logN)Ѕ где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Сортировка посредством выбора Идея метода довольно проста: найти наибольший элемент файла и по-ставить его на место N, найти следующий максимум и поставить его на место N-1 и т.д. до 2-го элемента. Время работы алгоритма t примерно оценивается формулой: t=a*NЅ+b*N* logN где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Использование связанного списка для хранения информации о проме-жуточных максимумах. В алгоритме максимум среди K[1] ... K[j-1] определяется в цикле от j-1 до 1 c целью обеспечить меньшее число обменов в случае равенства ключей и сохранении прежнего порядка равных элементов. Однако, если изменить порядок просмотра элементов на противоположный и изменить структуру данных, введя дополнительные указатели, можно пример-но в два раза сократить число повторений в цикле поиска максисмума. Каждый ключ K[i] снабжается указателем L[i] на элемент, максимальный среди первых i-1 элементов . Тогда после обмена элементов K[j] и K[m] поиск максимума в следующем цикле по j можно осуществлять среди элементов K[L[m]] ... K[j] при началь-ных значениях X=K[L[m]], m=L[m], т.к. максимум может "обновиться" только за счет элементов, лежащих правее локального максимума. Таким образом среднее количество просматриваемых при поиске максимума элементов со-кращается примерно в два раза. Время работы алгоритма t примерно оценивается формулой:t=a*NЅ + b*N*logN где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Сортировка посредством слияния Алгоритмы сортировки этого класса основываются на объединении нескольких (часто двух) уже упорядоченнх файлов. Рассмотренные далее алгоритмы выбирают из исходного файла упорядоченные отрезки и объединяют их в более длинные. Естественное двухпутевое слияние Этот алгоритм ищет упорядоченные отрезки с двух концов файла ипереписывает их по очереди также в оба конца. Повторяя эту процедуру в цикле, мы приходим к середине файла, что означает окончание сортировки. Элементы файла пересылаются из одной области в другую, меняя направление пересылки. Для запоминания направления пересылки служит переменная s, принимающая значения TRUE и FALSE попеременно. Другой логический признак f служит сигналом продолжения-окончания алгоритма, если все области слились в конце концов в одну. Переменная в принимает попеременно значения +1 -1 и указывает направление просмотра файла: вперед или назад.Операция <-> обозначает обмен значениями двух переменных. Операция Џ обозначает инверсию логической переменной или выражения. Время работы алгоритма t примерно оценивается формулой: t=a*N*lgN + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. Простое двухпутевое слияние. В алгоритме естественного двухпутевого слияния упорядоченный отрезки файла определялись случайным расположением элементов в исходном файле. В данном алгоритме длина отрезков фиксируется на каждом шаге. В исходной файле все отрезки имеют длину 1, после первого шага она равна 2, после второго 4, после третьего - 8, после к-го шага -2 в степени к. Время работы алгоритма t примерно оценивается формулой: t=a*N*lgN + b*N где a,b - неизвестные константы, зависящие от программной реализации алгоритма. 1.2 ОБОСНОВАНИЕ ВЫБОРА МЕТОДА РЕШЕНИЯ ЗАДАЧИ Сортировка массива быстрым методом является прекрасным примером целесооразности использования рекурсивного обращения в программированние на языке Си . Метод быстрой сортировки был предложен К. А. Р. Хоором в 1962г. Предложенная версия быстрой сортировки , разумеется , не самая быстрая среди всех возможных ,но зато она из самых простых . Основная стратегия ускорения алгоритмов сортировки - обмены между как можно более дальними элементами исходного файла - в методе быстрой сортировки реализована за счет того, что один из ключей в исходном файле используется для разделения его на два подфайла так, чтобы слева от выбранного элемента находились только элементы с меньшими ключами,а справа - только с большими. Алгоритмы сортировки методом слияния основываются на объединении нескольких (часто двух) уже упорядоченнх файлов. Этот алгоритм ищет упорядоченные отрезки с двух концов файла и переписывает их по очереди также в оба конца. Повторяя эту процедуру в цикле, мы приходим к середине файла, что означает окончание сортировки. 3. РАЗРАБОТКА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ Алгоритм решения задачи предельно прост. Функция main() явлвется функцией меню и выполняет опрос клавиатуры . В зависимости от нажатой клавиши выполняет соответствующие действия программы. Для чтения информации о программе из файла text.hlp используется функция help(), которая работает с файловым выводом. Функция file() основная так как с её помощью выполняется сортировка массива (вызов функций qqsort() и srecmg()) определение времени сортировки вызов функции построение гистограмм. Массив состоит из случайных чисел вводимых в него функцией генератора случайных чисел. Далее функция file() вызывает соответствующие функции сортировки, засекает время сортировки соответствующим способом , и заносит это время в массив simvol[]. Далее данные из массива передаются в функцию grafix(), где они используются при выводе на экран гистограмм в графическом режиме . Программа предусматривает случаи отсутствия некоторых программных элементов. В этом случае вызывается функция Error(), которая создаёт окно сообщения в которое вписываются характеристика ошибки. Так программа не будет выполнятся если не найден файл “text.hlp” или драйвер EGAVGA.BGI . 3.1 ОПИСАНИЕ ПРОГРАММЫ Данная программа называется “TEST” (имя исполняемого файла test.exe) и предназначена для анализа методов сортировки одномерного массива. Программа работает на IBM совместимых компьютерах семейства х86 начиная с 286 и выше, в операционной системе типа Ms-DOS 3.0 и выше. Программа содержит пять основных функций: main(), file(), qsort(), srecmg(), grafix(). Все переменные, используемые в программе являются локальными. Функция main() содержит пункты меню и вызывает другие исполняемые функции в зависимости от нажатия предложеных функциональных клавиш F1, F2 и F10. Каждая из этих функций работает автономно и независимо от двух других. Программа реализована как в псевдографическом так и в графическом режиме (в связи с чем она может компилироваться только в DOSовских версиях BorlandC++ или BorlandC). В графическом режиме она выводит на экран гистограмму которая характеризует время сортировки массивов двумя способами. Программа использует как стандартный так и файловый ввод-вывод информации . Стандартный ввод представлен запросом программы на ввод функциональных клавиш , которые задают характер выполняемого действия . Файловый ввод-вывод используется в функции help(), для вывода на экран информации о разработчике программы , её функциональных клавишах и о возможных ошибках в процессе выполнения. Кроме того программа работает с функцией времени clock() и переменными времени типа clock_t. Так же программа содержит стандартные функции языка Си, описанные в библиотеках: <string.h>, <stdlib.h>, <time.h>, <stdio.h>, <conio.h>,<graphics.h>. Ниже перечислены библиотеки с функциями и дано краткое описание использованных в программе стандартных функций. Из библиотеки <time.h>: clock() – эта функция возвращает время , фиксируемое процессором от начала счета программы , или –1, есле оно не известно . Для возвращения этого времени в секундах применяется формула clock()/CLK_TCK. Из библиотеки <stdlib.h>: rand() – эта функция выдаёт псевдо случайное число в диапазоне от 0 до RAND_MAX не меньше 32767 . exit() – вызывает нормальное завершение программы . Из библиотеки <stdio.h>: printf() – эта функция осуществляет вывод строки на экран. fopen() – эта функция открывает файл с заданным именем и возвращает поток или NULL, если попытка открытия оказалась неудачной . fclose() – эта функция производит дозапись ещё незаписанных буферизированных данных , сбрасывает нечитанный буферизированный ввод , освобождает все автоматические запрошенные буфера , после чего закрывает поток . Возвращает EOF в случае ошибки и 0 в противном случае . fgetc() – эта функция возвращает следущуюлитеру из потока stream в виде unsignedchar или EOF, если исчерпан файл или обнаружена ошибка . puts() – пишет стринг s и литеру новая – строка в stdout . Возвращает EOF в случае ошибки , или неотрицательное значение , если запись прошла нормально . Из библиотеки <conio.h> textbackground() – с помощью этой функции устанавливается цвет фона для функции cprintf(). textcolor() – с помощью этой функции устанавливается цвет текста для функции cprintf(). clrscr() – функция очистки экрана, цветом установленным функцией textbackground(). cprintf() – с помощью этой функции осуществляется вывод строки с учётом цветов установленных функциями textbackground(), textcolor(). _setcursortype() – с помощью данной функции осуществляется изменение режима отображения курсора. Данных режимов в Си всего три – NOCURSOR (курсор выключен), SOLIDCURSOR (курсор в виде сплошного блока) NORMALCURSOR (обычный курсор). getch() – функция getch осуществляет считывание первого единственного символа с клавиатуры, используется при считывании клавиш курсора при перемещении по окну выбора режима работы программы. gotoxy() – эта функция перемещает курсор в нужную часть экрана, обычно используется перед функцией cprintf(). В этой библиотеке описаны все символические константы цветов используемые функциями textbackground(), textcolor(). В ней также описаны все типы курсоров используемых функцией _setcursortype(). 3.1.1 ОПИСАНИЕ ФУНКЦИИ main() Функция main имеет тип void и является функцией меню. Main выполняет опрос клавиатуры и в зависимости от нажатой функциональной клавиши выполняется соответствующее действие (вызов помощи , тестирования и выход из программы). Эта возможность реализована благодаря конструкции множественного выбора switch . Функция имеет одну локальную переменную press имеющую тип char . Она воспринимает символ с клавиатуры без вывода на экран и используется в конструкции switch при переходе к другой выполняемой функции . В данной функции вызывается вспомогательная функция windows() , которая создаёт псевдографический интерфейс при запуске программы. При выборе пункта выхода из программы стандартная функция textbackground() создаёт черный экран ,а функция exit() совершает выход из программы. При вызове функции помощи (help()) программа обращается к этой функции, которая считывает и выводит информацию файловым способом. Вызываемый фаил хранится под именем test.hlp и при его отсутствии выдаётся окно сообщения : «Фаил text.hlp не найден». Вызов функции построения гистограмм выполняется при нажатии клавиши F2. При этом функция main() обращается к функции file() . 3.1.2 ОПИСАНИЕ ФУНКЦИИ srecmg(). Для построения упорядоченного списка В’ из списка В=<к1,к2,...,кn> при сортировке слиянием список В делится на n подсписков В1=<к1>, В2=<к2> , ... , Вn=<кn> длины 1. Потом совершается процедура прохождения в которой m≥2 упорядоченных списков В1,В2,...,Вm меняются на m/2 ( или (m+1)/2) упорядоченных списков которые создаются слиянием B2i-1и B2i (2i≤m) и суммированием Bmc непарным m. Процесс повторяется до появления одной последовательности длины m. Количество действий , необходимых для сортировки слиянием , равна nlog2n, потому что за одно прохождение выполняется n сравнений , а всего необходимо осуществить log2n прохождений . Сортировка слияниием дастаточно эффективно и используется при больших значения n. Функция srecmg() является рекурсивной , и сортирует массив а[n]. За каждым вызовом массив для сортировки делится на две части – от а[0] до a[i-1] и от a[i] до a[n] , каждая из которых сортируется отдельно , а потом выполняется их слияние. Слияние выполняется при помощи вызываемой функции merge() в которую передаётся указатель на массив , текущий номер элемента массива и количество элементов массива . Параметрами функции merge() являются массив w[ ] ,его длина l/2 и длина первой части массива l1 .Функция merge() выполняет слияние подмассивов , образуя на их месте упорядоченный массив w[0],w[1],...,w[l2-2],w[l2-1] . 3.1.3 ОПИСАНИЕ ФУНКЦИИ qqsort() Быстрая сортировка состоит в том , что список В=<k1,k2,…,kn> реорганизуется в B’,<k1>,B”,где В’ – подсписок В с элементами , не большими k1 , а B” – подсписок В с элементами большими k1. В списке В’,<k1>,В” элемент К1 уже находится на месте где он должен быть в отсортированом списке. Дальше к спискам В’ и В’’ применяется упорядованичение быстрой сортировкой . Рекурсивная функция qqsort упорядоваечет быстрой сортировкой участок масcива целых чисел первый элемент которого указывается показателем v[left] , последний – показателем v[right]. Если участок масива более чем из двух элементов , v[left] – low >1,то находится делящий элемент и переносится в V[0]. Пременной last присваивается значение первого элемента массива left. Затем массив делится на две части, элементы которых соответственно больше и меньше last. Далее функция выполняет перезапоминание делящего элемента и вызывает себя для разбитых подсписков . Обмен элементов выполняется при помощи функции swap() , в которую из функции qqsort() перелаётся указатель на массив и элементы , место-положение которых в массиве нужно обратить . Время построения списка зависит от его начального состояния. Время будет минимальным , если каждый шаг раздела дает подсписки В’ , B’’ приблизительно одинаковой длины ; тогда необходимо (nlog2 n) шагов . Если начальный список мало чем отличается от обычного отсортированного то необходимо (n^2)/2 шагов . Быстрая сортировка требует дополнительной памяти порядка O (log2n) для исполнения рекурсивной функции qqsort() (неявного стэка). 3.1.4 ОПИСАНИЕ ФУНКЦИИ grafix() Функция grafix() имеет тип void и параметр simbol[2] – массив скорости выполнения сортировки . Эта функция вызывается при построении гистограммы и работает в графическом режиме о чем информирует строка initgraph(&gdriver, &gmode, ""), которая устанавливает систему в графический режим , определяет характеристику видеодрайвера. Если переменная errorcode не получает значение grOk , то дальнейшее выполнение программы не возможно так как графический режим не установлен (о чем выводится сообщение). В массиве simvol[] определяется больший элемент , столбец которого устанавливается в 100% . Строка: bar3d(midx + otst + siz * n, midy -CopySimvol[n], midx + siz* (n+1 ), midy, 15, 1); создаёт 3D-изображения гистограмм, высота которых определяется массивом CopySimvol[n]. Цвет выводимых элементов изображения устонавливает функция setcolor(), а все выводимые линии строятся функцией line(). Текст выводится при помощи функции outtextxy(). Если текст должен выводиться вертикально то функции settextstyle() задаётся параметр VERT_DIR. После вывода на экран изображения выполняется опрос клавиатуры и если пользователем была нажата клавиша “ESC”, то программа возвращается в функцию file() и дальше в функцию main(), где снова ожидает нажатия необходимой клавиши . Функция closegraph() закрывает графический режим . 3.2 РУКОВОДСТВО ПРОГРАММИСТА Данная программа предназначена для анализа методов сортировки массивов быстрой и слиянием . Программа может работать на IBM совместимых компьютерах семейства х86 начиная с 286 и выше, под управлением операционных систем Ms-DOS 3.0 и выше и Windows 9x. Данная программа компилировалась с использованием BorlandC++ 3.1.Компилия программы в версиях BorlandC++ сконфигурированных под Windows(таких как BorlandC++4.5, BorlandC++5.2 и выше) не возможна так как графический режим [2] функционирует только в версиях сконфигурированных под DOS.Программа не требует от пользоватля ввода массива для его сортировки. Этот массив создается специальной функцией языка Си – генератор случайных чисел[3]. Программа была разработана на компьюторе с низкой тактовой частотой(75MГц). А так как в программе используется секундомер, то тактовая частота компьютора, на котором демонстрируется программа, влияет на точность выводимых результатов. Поэтому не советуется пользоваться ею на компьюторах с тактовой частотой выше 150МГц. Хотя в противном случае скорость сортировки значиельно увеличивается.Листинг программы приведён в приложении 1.Программа не предусмотренна для работы в режиме командной строки. Если вводимая пользователем функциональная клавиша не предусмотренна программой, то она выполняться не будет до тех пор, пока пользователь не введет соответствующий символ. Если программа не находит некоторых нужных для ее выполнения файлов, то выдается окно сообщения об ошибке с текстом причины. Функция error() вызывается везде, где появляется ошибка.(создает окно сообщения). В случае необходимости программу можно остановить в любом месте её исполнения следующими комбинациями клавиш: Ctrl C или Alt X .Вызов программы осуществляется путём запуска файла test.exe, при этом программа будет работать в интерактивном режиме. Окно помощи программы содержит: название программы, данные о разработчике, назначение, функциональные клавиши используемые в программе, и возможные проблемы при ее выполнении. 3.3 РУКОВОДСТВО ОПЕРАТОРА Основной функцией данной программы является определение времени сортировки массивов методами быстрой и слиянием. Путем незначительных изменений в программе, можно приспособить программу специально для сортировки массивов. Данная программа (test.exe) является единым исполняемым модулем и не требует наличия любых других установленных программных средств. Она так же не требует установки на компьютер, каких бы то ни было специфических аппаратных средств.Контрольный пример выполнения программы приведён в приложении 2.Программа может работать лишь в интерактивном режиме. Сортировка массива с большим числом элементом на современном компьютере займет всего несколько секунд и зависит от размера сортируемого массива.После загрузки программы оператору будет предложено нажать необходимую клавишу для продолжения выполнения программы , для вывода информации о программе или для выхода. Если программа не содержит файла text.hlp или не найдан драйвер EGAVGA.BGI, то программа выдаёт окно сообщения об ошибке. Если программа содержит все необходимые элементы, то она выдаст окно сообщния о возможности выполнения анализа сортировки. Если программа получила разрешение на начало процесса сортировки, то она выполняет его и после завершения выводит на экран в графическом режиме результаты о анализе сортировок. В случае необходимости программу можно остановить в любом месте её исполнения следующими комбинациями клавиш: Ctrl C или Alt X . В таком случае программа не выполнит ни каких действий.Окно помощи программы содержит: название программы, данные о разработчике, назначение, функциональные клавиши используемые в программе, и возможные проблемы при ее выполнении. ЗАКЛЮЧЕНИЕ В результате выполнения курсового проекта была написана программа, анализирующая сортировку массивов способами быстрой и слиянием. Программа обладает высоким параметром быстродействия, маленьким размером и не требовательна к системным ресурсам компьютера. В качестве недостатка программы можно отнести то, что точность выполнения программы зависит от тактовой частоты компьютера. Этот недостаток можно решить путём изменения количества сортируемых элементов массива. Программа может быть преобразована для использования в целях сортировки массивов вводимых пользователем. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ 1. Шолмов Л.И. Руководство по турбо Си. М.: Наука, 1994. – 94-98с. 2. Уинер Р. Язык Турбо Си : Пер. с англ. -М.:: Мир, 1991. – 384 с. 3. Керниган Б.В, Ричи Д.М. Си для профессионалов. М.: Энергия, 1996.– 213 с. 4. Грейд Дж. Математическое программирование. М.: Наука, 1987. – 241 с. 5. Либерман М. Алгоритмы сортировки массивов. М.: Наука, 1997. – 43-81с. Приложение 1 ЛИСТИНГ ПРОГРАММЫ // листинг программы сортировки массивов разработанная Андрусевичем Б.И. #include <stdio.h> #include <dos.h> #include <graphics.h> #include <stdlib.h> #include <conio.h> #include <string.h> #include <time.h> //-------------< Создание оболочки >------------- void windows(int w) { int n; _setcursortype(0); window(1, 1, 80, 25); // Выделениеокна textbackground(BLACK); // Цветфона clrscr(); // Очистка экрана window(1, 25, 80, 25); // Выделение окна textbackground(GREEN); // Цвет фона clrscr(); // Очистка экрана window(1, 25, 80, 25); textcolor(BLACK); // Цвет текста if (w == 1) // Проверка на выбор окна { n = 21; cprintf(" Помощь Тест Выход"); window(2, 25, 4, 25); textcolor(RED); // Управляющие клавиши cprintf("F1"); // основного окна window(13, 25, 15, 25); cprintf("F2"); window(22, 25, 25, 25); cprintf("F10"); textbackground(BLUE); } else { n =22; cprintf(" Выходизпомощи "); window(3, 25, 6, 25); textcolor(RED); // Управляющиеклавиши cprintf("Esc"); // окнапомощи textbackground(CYAN); } window(1, 1, 80, 25); // Прорисовкарамки textcolor(WHITE); cprintf("+------------------------------------ Тест ------------------------------------+"); for (int k = 0; k < n; k++) cprintf("¦ ¦"); cprintf("+------------------------------------------------------------------------------+"); if (w == 1) { window(2, 2, 79, 2); puts(" Эта программа демонстрирует сортировку массива двумя методами:"); window(2, 3, 79, 3); puts(" быстрым методом и методом слияния. После чего определяется время сор-"); window(2, 4, 79, 4); puts(" тировки массива каждым методом и результат выводится в виде гисто-"); window(2, 5, 79, 5); puts(" граммы."); window(2, 6, 79, 6); window(20, 10, 60, 15); textcolor(WHITE); textbackground(LIGHTGRAY); cprintf("+------------------------------------------------------------------+"); cprintf("¦ НЕОБХОДИМЫЕ ФАЙЛЫ ПРИСУТСТВУЮТ ¦"); cprintf("¦ (для тестировния нажмите F2) ¦"); cprintf("+------------------------------------------------------------------+"); closegraph(); } } //------------< Окно сообщения ошибок>----------- void Error() { window(20, 10, 60, 15); textcolor(WHITE); textbackground(LIGHTGRAY); cprintf("+----------------- Ошибка ----------------+"); cprintf("¦ ¦ "); cprintf("¦ ¦"); cprintf("¦ ¦"); cprintf("+---------------------------------------------+"); } //-------------< Функцияпомощи >---------------- help() { int n = 1; FILE *hl; // Указатели на файл char string[78]; if ((hl = fopen("test.hlp", "r")) != NULL) // Проверка на открытие файла { windows(0); window(2, 2, 78, 23); textcolor(BLACK); while (fgets(string, 78, hl) != NULL && n < 23) { gotoxy(1, n++); // Построчный вывод файла cputs(string); // помощи } window(36, 1, 44, 1); printf(" Помощь "); // Вывод заголовка помощи while (27 != getch()); } else{ Error(); window(29, 12, 52, 12); textcolor(BLACK); cprintf("Файл TEST.HLP ненайден"); getch(); windows(1); } fclose(hl); windows(1); return 0; } //--------< Функцияпостроениягистограмм>------- grafix(double simvol[2]) { double CopySimvol[2]; // Масивколичествасимволов long float max = 0; int gdriver = DETECT, gmode, errorcode; int midx = 50; // Обявление переменных int midy = 410; // с заданними начальными int i, s; // значениями int siz = 100; int otst = 10; int rovn = 45; char chis[2]; char buf[10]; initgraph(&gdriver, &gmode, ""); errorcode = graphresult(); // Записькодошибки if (errorcode != grOk) // Проверканаошибку { Error(); // Вызовфункцииокна window(26, 12, 54, 12); textcolor(BLACK); cprintf("Драйвер EGAVGA.BGI ненайден"); getch(); windows(1); return 0; } for (int y = 0; y < 2; y++) // Оприделениемаксимального if (max < simvol[y]) // числа max = simvol[y]; for (int b = 0; b < 2; b++) // Оприделениевысотыстолбцов CopySimvol[b] = simvol[b] * 200 / max; setfillstyle(CLOSE_DOT_FILL,9); for (int n = 0; n < 2; n++) // Построениестолбцовилиний { setcolor(BLUE); bar3d(midx + otst + siz * n, midy - CopySimvol[n], midx + siz* (n+1 ), midy, 15, 1); setcolor(BROWN); line(midx + rovn + siz * n, midy + otst, midx + rovn + siz * n, midy + otst * 2); sprintf(chis, "%d", n + 1); setcolor(GREEN); outtextxy((midx + rovn + siz * n) - 2, midy + otst * 2, chis); setcolor(CYAN); sprintf(buf, "%lf", simvol[n]); outtextxy((midx + rovn + siz * n) - 15, midy - CopySimvol[n] - rovn, buf); } setcolor(BROWN); line(midx, 100, midx, midy + otst); // Построениеоси Y line(midx, midy + otst, 280, midy + otst); // Построениеоси X line(midx - otst, midy - 200, midx, midy - 200); // Построение line(midx - otst, midy - 100, midx, midy - 100); // линии settextstyle(DEFAULT_FONT, HORIZ_DIR, 1); setcolor(GREEN); outtextxy(535, 460, "ESC "); outtextxy(10, 205, "100"); outtextxy(10, 305, "50"); outtextxy(350, 235, "1. Сортирвка массива быстрым"); outtextxy(350, 250, " методом"); outtextxy(350, 280, "2. Сортирвка массива методом"); outtextxy(350, 295, " слияния"); setcolor(LIGHTBLUE); outtextxy(300, 423, "метод"); outtextxy(570, 460, "Выход"); settextstyle(DEFAULT_FONT, HORIZ_DIR, 2); outtextxy(220, 30, "ГИСТОГРАММА"); settextstyle(DEFAULT_FONT, VERT_DIR, 1); outtextxy(48, 160, "время"); while (27 != getch()); // Проверка на символ ESC closegraph(); windows(1); return 0; } /*qsort:сортирует v[left]...v[right] повозрастанию*/ void qqsort( int v[], int left, int right) { int i,last; delay(1); void swap( int v[], int i, int j); if(left>=right) /*ничего не делается если*/ return; /* в массиве менее двух эл-тов */ swap(v,left,(left+right)/2); /*делящий эл-нт переносится в v[0]*/ last=left; for(i=left+1;i<=right;i++) /*делениеначасти*/ if(v[i]<v[left])swap(v,++last,i); swap(v,left,last); /*перезапоминается делящий элемент*/ qqsort(v,left,last-1); qqsort(v,last+1,right); } void swap( int v[], int i, int j) { long int temp; temp=v[i]; v[i]=v[j]; v[j]=temp; } /*SRECMG -- РЕКУРСИВНАЯ СОРТИРОВКА СЛИЯНИЕМ*/ void srecmg(a,n) int a[],n; { void merge( int*, int, int); int i; delay(1); if(n>1) {i=n/2;srecmg(a,i);srecmg(a+i,n-i);merge(a,i,n);} } /*merge--слияниедвухподсписков*/ #define MAX(x,y) ((y)<(x)?(x):(y)) void merge( int*w, int l1, int l2) { int*a,*pa,*pb,i; a=( int*)calloc(l2+2,sizeof( int)); pa=a;pb=a+l1+1; for(i=0;i<l1;i++) *pa++=w[i]; for(i=l1;i<l2;i++) *pb++=w[i]; *pa=*pb=MAX(w[l1-1],w[l2-1])+1; pa=a;pb=a+l1+1; for(i=0;i<l2;i++) w[i]=(*pa<*pb?*pa++:*pb++); free(a); } #define ww 700 //-------< Функция вызова разных методов >------- file() { void qqsort( int *, int,int); void srecmg( int*, int); double simvol[2]; int s; clock_t start,start2,end,end2; int t=0; int gener1[ww],gener2[ww]; //Генератор случайных чисел randomize(); //Устанавливает генератор в 0 for ( s=0 ; s < ww ; s++) { gener1[s]= ( rand()%100 ); // rand()-функциягенератора gener2[s] =gener1[s]; } { start=clock(); qqsort(gener1,0,ww-1); end=clock(); simvol[0] = ((end - start)/CLK_TCK); } { start2 =clock(); srecmg(gener2,ww); end2=clock(); simvol[1] = ((end2 - start2)/CLK_TCK); } grafix(simvol); // Вызов функции построения гистограмм windows(1); return 0; } //-------------------< Меню >-------------------- void main() { char press; windows(1); while (1) { press = getch(); // Опросклавиатуры switch(press) { case 59: help(); break; // Вызовпомоши case 60: file(); break; // Запуск гистограммы case 68: { // Выход из программы window(1, 1, 80, 25); textbackground(BLACK); clrscr(); exit(1); } } }} Приложение 2КОНТРОЛЬНЫЙ ПРИМЕР ВЫПОЛНЕНИЯ ПРОГРАММЫ В качестве примера возьмём исходный файл “Test.exe” и запустим его . На экране появляется окно собщения о наличии необходимых файлов. Для продолжения выполнения программы пользователь нажимает клавишу F 2 , в результате чего на экране появляется гистограмма , характеризующая скорость выполнения сортировки массивов. Воспользовавшись клавишей Esc , пользователь выходит с графического режима в режим отображения меню. При нажатии пользователем клавиши F 1 на экране появляется окно помощи которое содержит название программы, данные о разработчике, назначение, функциональные клавиши используемые в программе, и возможные проблемы при ее выполнении.Нажатие клавиши Esc приводит к закрытию окна помощи. Для выхода из программы пользователь должен нажать клавишу F 10 .
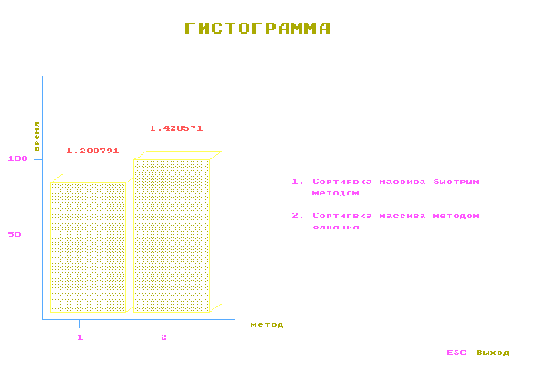
Пример выводимой гистограммы. |