Реферат: Спектральная теория операторов
|
Название: Спектральная теория операторов Раздел: Рефераты по математике Тип: реферат | |
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Спектральная теория операторов Саранск 2009 СОДЕРЖАНИЕ Введение………………………..………………………………………………..4 1 Линейный оператор…………………………………………………………...4 1.1 Понятие линейного оператора………………………………………...4 1.2 Линейные преобразования………………………………………….....4 1.3 Сопряжённый и самосопряжённый оператор………………………..5 2 Спектральная теория компактных операторов……………………………...7 2.1 Спектр оператора……………………………………………………...7 2.2 Понятие об ограниченном операторе………………………………...8 2.3 Понятие о компактном операторе…………………………………...13 3 Спектральная теория компактных операторов……………………………….16 3.1 Множество значений компактного оператора……………………........16 3.2 Собственное значение компактного оператора……………………..18 Заключение……………………………………………………………………...25 Список использованных источников……………………………………..…...26 ВВЕДЕНИЕДанная курсовая работа посвящена спектральной теории операторов. В отдельной главе более подробно рассматривается спектральная теория компактных операторов. Важнейшими задачами этой теории являются утверждения о приведении изучаемых операторов к так называемому диагональному виду – спектральные теоремы, утверждения о свойствах спектра и собственных значениях. Цель данной курсовой работы – познакомить тех, кто интересуется математикой со спектральной теорией операторов, в частности, со спектральной теорией для компактных операторов. Данная курсовая работа состоит из трёх глав: 1) Линейный оператор; 2) Спектральная теория операторов; 3) Спектральная теория компактных операторов. В первой главе рассматривается понятия линейного оператора, линейные преобразования, сопряжённый и самосопряжённыйоператор. Во второй главе рассматривается понятие спектра оператора, теорема для замкнутого линейного оператора, спектральный радиус,понятие об ограниченном операторе и компактных операторах, а также теорема, являющаяся важным характеристическим свойством компактных операторов. В третьей главе рассматриваются множество значений компактного оператора, собственные значения компактного оператора. В каждой главе приводятся решённые примеры. 1 Линейный оператор 1.1 Понятие линейного оператора Функцию, множество значений которой принадлежит полю скаляров, называют функционалом. Вообще функция может быть определена не на всем гильбертовом пространстве, а лишь на некотором его подмножестве. Это подмножество называют областью определения функции. Множеством значений функции называют множество, в которое эта функция отображает свою область определения. Для удобства условимся обозначать область определения через D, гильбертово пространство ее содержащее, — через Н1 множество значений — через R а содержащее его пространство — через Н2 . Определение 1.1 Оператор (преобразование) L называется линейным, если его область определения в является линейным подпространством (плотным или нет) и он линеен на D L( Множество линейного оператора также является линейным подпространством. 1.2 Линейные преобразования Определение 1.2 Графиком G(T) линейного преобразования Т называется подпространство в произведении подпространств Н1
G(T) = Определение 1.3 Линейное преобразование Т называется замкнутым, если его график функции замкнут в Н3
. Иначе замкнутость оператора Т можно определить так: пусть xn
Отметим, что, как правило, дифференциальные операторы замкнуты. Этот факт и определяет необходимость рассмотрения класса замкнутых операторов. Определение 1.4 Линейное преобразование Т называется ограниченным, если в = Н1 и sup Определение 1.5 Нормой линейного ограниченного преобразования T называется число
Линейное преобразование ограничено, если оно непрерывно в начале координат. Тогда оно непрерывно в каждой точке. Ограниченное линейное преобразование, очевидно, непрерывно. Пусть Т1 , Т2 — линейные ограниченные операторы, отображающие пространство Н1 в Н2 . Тогда ясно, что сумма T1 +Т2 также является линейным ограниченным оператором. Кроме того,
В силу определения (
Следовательно, {Tn
x} является последовательностью Коши пространства H2
, ее предел обозначим через Тх. Очевидно, что оператор Т линеен и ограничен. Если n>N(e) и
1.3 Сопряжённый и самосопряжённый оператор Определение 1.6 Пусть T — линейный ограниченный оператор из H1
в Н2
сопряженный оператор T* (определенный на Н2
и принимающий значения в Н.) определяется условием у = Т*х
в том и только том случае, если существует вектор у такой, что [y,z] = [x,Tz]
для любого z Определение 1.7 Пусть H1 =H2 =H. Оператор L c плотной областью определения, называется самосопряжённым, если L=L* [9]. 2 Спектральная теория операторов 2.1 Спектр оператора В приложениях часто возникает следующая задача: задан оператор Т,
найти элемент х
такой, что Тх
=у,
где элемент у
задан. В общем случае множество решений может оказаться либо пустым, либо содержать слишком много элементов. Можно рассмотреть несколько более общую задачу: найти элемент х
такой, что Определение2.1 Пусть Т
— замкнутый линейный оператор, отображающий пространство Н
в себя. Комплексное число Если комплексное число X
не принадлежит точечному спектру оператора Т,
то, безусловно, можно определить оператор ( Обратный оператор ( Теорема 2.1 Пусть Т — замкнутый линейный оператор и число
Доказательство. Оператор (
Определение2.2 Множество комплексных чисел Пример 2.1. Пусть H
=
L
2
(0,
1),aD
— класс функций, производные которых тоже принадлежат L2
(0, 1). Для функций f 2.2 Понятие об ограниченном операторе Теорема 2.2 Пусть Т — ограниченный оператор, отображающий пространство Н в себя. Тогда Доказательство.Основной шаг заключается в доказательстве сходимости ряда
для всех |
абсолютно сходится при |z|>lim ( Следствие 2.1 Спектр произвольного замкнутого оператора является замкнутым множеством. Спектр ограниченного оператора не пуст. Доказательство. Сначала докажем, что резольвентное множество произвольного замкнутого оператора открыто. В случае, если резольвентное множество замкнутого оператора пусто, то доказывать нечего. Предположим, что резольвентное множество не пусто и содержит число (I+ ( Докажем, что
Пусть x (
Если x
Таким образом, оператор R ( λ ; T ) — резольвента. Следовательно, резольвентное множество открыто. Более того, имеем R
(
при ||λ R (λ0 ; T )||< 1. Таким образом, если L(∙) — линейный непрерывный функционал на L
(
H
,
H
),
то функция L
(
R
(
K
;
T
))
оказывается аналитической на резольвентном множестве оператора Т.
Рассмотрим теперь случай, когда оператор Т
ограничен. Предположим, что его спектр — пустое множество. Тогда для любого линейного непрерывного функционала L
(∙)
аналитическая функция L
(
R
(λ;Т))
определена на всей комплексной плоскости и, кроме того, она ограничена в бесконечности, поскольку ||λR
(λ; Т)
||≤(1– Определение 2.3 Ограниченный оператор называется квазинильпотентным,если его спектральный радиус равен нулю [6]. Спектр квазинильпотентного оператора содержит лишь нулевую точку. Пример2.2 Пусть H = L 2 (0, 1). Определим оператор Т соотношениями Tf = g, g(t)= Тогда оператор Т
линеен и ограничен. Используя неравенство Шиарца,найдем λf
(
t
)— f — непрерывная функция. Далее, уравнение λ
f
(
t
)-
имеет единственное решение
и потому спектр оператора Т может содержать лишь нулевую точку. Это можно доказать заметив, что оператор Т квазиниль-потентен:
Как было доказано выше, спектр ограниченного оператора не может быть пустым. Следовательно, спектр оператора Т состоит из нулевой точки. С другой стороны, в рассматриваемом случае, нуль не является собственным значением, поскольку из условия Tf = 0 следует, что f = 0. Отсюда следует, что Т-1 — замкнутый линейный оператор, однако он неограничен. Это и следовало ожидать, поскольку T-1f = g означает, что g = f '. Пример 2.3 В общем случае нельзя указать эффективной процедуры отыскания спектра и резольвентного множества заданного оператора. Однако, для интегральных операторов такой общий метод существует; он заключается в дифференцировании необходимое число раз равенства, определяющего точку спектра с целью получения определяющего дифференциального уравнения. Рассмотрим, например, оператор
Рассмотрим сначала точечный спектр этого оператора. Если функция L(•) из H является собственным вектором, то
Дифференцируя обе части этого равенства, получим дифференциальное уравнение f
(
t
)
=
его общее решение имеет вид f ( t )= k - ta , где k — произвольное постоянное число, а а = (1 –λ)/λ.С другой стороны, из условия
следует, что l
+2
Re
((1– λ)/ λ)=0
или Re
(1/ λ)> Таким образом, всякое комплексное число λ, удовлетворяющее этому условию, принадлежит точечному спектру. Так как спектр — замкнутое множество, то {λ; -
Предполагая дифференцируемость соответствующих функций, получим
Отсюда следует, что
где k
— константа. Если ограничиться рассмотрением тех
Условие 1 + 2
Re
(
l
— Определение 2.4 Ограниченный линейный оператор, отображающий пространство Для любого ограниченного линейного оператора операторы Т*Т и ТТ* неотрицательно определены [8]. 2.3 Понятие о компактном операторе Определение 2.5 Ограниченный линейный оператор, отображающий пространство H Важное характеристическое свойство компактных операторов определяется следующей теоремой [7]. Теорема 2.3 Пусть Т
— компактный оператор, отображающий пространство H Доказательство.Пусть оператор Т
компактен, а {хп
}
— слабо сходящаяся, скажем к х0
, последовательность из Н
для некоторого числа М,
О < М
< [ y , h ] = lim [ Txnk , h ] = lim [ xnk , T * h ] =[х0 , T * h ] = [Тх0 , h ], откуда у=Тх0 , так что у не зависит от выбора конкретной подпоследовательности, а значит, limTxn = у. Обратно, пусть Т
— ограниченный линейный оператор, переводящий любую слабо сходящуюся последовательность в сильно сходящуюся. Пусть В
— ограниченное множество в Н Пример 2.4 Пусть (
Тогда оператор L, определенный соотношениями Lf=g, g(t)= линейнои непрерывно отображает пространство Н1
=
L
Пусть ei
— единичный вектор евклидова пространства R
q
. Тогда для любого t
[
определяет линейный непрерывный функционал на пространствеH
1
. Следовательно, для каждого t gn
(
t
)=
g
(
t
)
= R
(
t
,
s
)
f
(
s
)
d
Можно применить теорему Лебега о почленном интегрировании последовательности. Следовательно,
при n 3 Спектральная теория компактных операторов 3.1 Множество значений компактного оператора Спектральная теория характеризует спектры и резольвентные множества операторов. Исследование интегральных операндов по существу эквивалентно изучению интегральных уравнений. По своим свойствам компактные операторы близки к конечномерным (матричным) операторам. Кроме того, последние играют большую роль в приложениях. Пусть Т— компактный оператор, отображающий пространство Нв себя. Тогда, если пространство бесконечномерно, то нуль должен принадлежать спектру, поскольку тождественный оператор Т-1 Тне является компактным. Напомним, что в дальнейшем пространства рассматриваются над полем комплексных чисел. Лемма 3.1 Для любого Доказательство. Пусть {уп
}
— сходящаяся последовательность из множества значений оператора ( М = {х: Тогда М –
замкнутое подпространство Н.
Обозначим через Р
оператор проектирования на подпространство М
и положим zn
=хп
–Рхп
.
Предположим, что ||zn
||
В силу сходимости {уп
}
последовательность hn
сходится к нулю. Так как ||
Отсюда, в силу сильной сходимости T Лемма 3.2 Предположим, что Доказательство. Достаточно показать, что
Обозначим через Ek
подпространство, порожденное элементами {
f
0
,
...,fk
}.
Докажем, что dimEk
> dimEk
для всех k fk
= Следовательно, Tfk
= С другой стороны, Tfk = Xfk — Tfk -1 . Таким образом,
или
Следовательно, противоположное утверждение остается верным для (
k
–1), и потому оно справедливо и для случая k
=
1, что невозможно. Далее, если dimEk
> dimEk
-1
,
то существует ортонормированная последовательность векторов {е
k
}
такая, что ek
ортогонален подпространству Ek
-1
.
Но [ 3.2 Собственное значение компактного оператора Лемма 3.3 Предположим, что ненулевое комплексное число Доказательство. Применяя предыдущую лемму, получим, что множество значений оператора ( Теорема 3.1 Пусть Доказательство. Достаточно показать, что если число Лемма3.4 Пространство собственных функций, отвечающих ненулевому собственному значению, конечномерно. Доказательство.Пусть Лемма 3.5 Последовательность {Хп } ненулевых и попарно различных собственных значений оператора Т может иметь предельной точкой лишь нуль. Точно так же, как и в конечномерном случае, собственные векторы, соответствующие различным собственным значениям, линейно независимы. Действительно, пусть Тх
= xm Следовательно,
и потому
Отсюда следует, что т
может быть уменьшено на единицу, что противоречит определению целого m
. Обозначим через Рт
оператор проектирования на подпространство Ет
,
порожденное элементами {х,
..., хт
}.
Оператор Т
отображает подпространство Е
m
в себя. Положим zm
= xm
—
Pm
-1
xm
.
Тогда zm
Теорема3.2 Спектр компактного оператора содержит не более счетного числа точек и его предельной точкой может быть лишь нуль. Каждая ненулевая точка спектра является собственным значением. Компактный оператор может вообще не иметь собственных значений. Однако для самосопряженных компактных операторов это уже не так. Теорема3.3 Самосопряженный компактный оператор, отображающий пространство Н в себя, имеет по крайней мере одно собственное значение. Доказательство. Прежде всего докажем, что если оператор самосопряжен, то
Обозначим правую часть этого равенства через с.
Ясно, что с
По [Тх, у] + [Ту, х] = Следовательно, |[Тх, у] + [Ту,х]|≤1/2{|[Т(х + у), х+у] + [Т(х-у),х-у]|}≤ ≤ 1/2 c {|| x + y ||2 +|| x – y ||2 }= c (|| x ||2 +|| y ||2 ) (3.13) Tак как оператор Т самосопряжен, поэтому в случае вещественного гильбертова пространства |[Тх, у]|≤
c или |[Тх, у]|≤с
для всех || х
|| = || у
|| –1. Следовательно, или |[Тх, у]|≤с
|| х
|| *|| у
||, или ||
T
||
< с.
Если исходное пространство рассматривается над полем комплексных чисел, то положим [
Tx
, у] =
| [Тх, у]
|ei [Т
x
1
,
y
1
] + [Ту, х1
] =
с( Полагая || х
|| = || у
|| = 1, получим [
Tx
, у] || х n ||= 1, lim |[ Txn , xn ]| = || T ||>0 Tак как последовательность {[Тхт
, хт
]}
состоит из вещественных чисел, то, переходя к подпоследовательности, можно считать, что она сходится либо к +||T||, либо к –||Т
||.
Обозначим этот предел через lim [ Txm , xm ] = [Тхо , хо ] = [у0 , х0 ] (3.15) Кроме того, 0<lim
|| Txm
– Но || у0
|| 2
= lim
|| Txm
||2
lim
|| Txm
– В силу сильной сходимости {
Txm
}
последовательность {хт
}
сильно сходящаяся. Следовательно, Тх0
= Точно так же, как и в конечномерном случае, собственные векторы самосопряженного оператора, соответствующие различным собственным значениям, ортогональны. Пусть теперь Т
— компактный самосопряженный оператор. Тогда, как мы знаем, его спектр состоит из дискретного множества вещественных собственных значений { М
i
= {х
: Тх = Пусть M 0 = {х : Тх = 0}. Для любого х из Н положим xi = Р i х, где Pi — оператор проектирования на подпространство Mi . Тогда 0 x
=
Следовательно, Tx
= xi
=
где е ij ,j = 1, …, mi , –базис подпространства М i , которое, как было показано выше, конечномерно. Замечание. Равенство Тх
= Т
= где I — тождественный оператор. Из этих равенств следует T
=
причем последовательность операторов проектирования { Ei } не убывает. Такого рода представление можно получить и для произвольного ограниченного оператора. Пример 3.1 Задача определения собственных значений и собственных функций компактного самосопряженного оператора в общем случае довольно сложна и, за исключением отдельных случаев, может быть решена лишь численно. Здесь мы рассмотрим лишь простейшую итерационную процедуру, позволяющую решить эту задачу приближенно. Пусть Т
—компактный самосопряженный оператор и х
произвольный ненулевой элемент пространства Н.
Предполагая Тх [Тхп
, хп
] = сходится к
если только || P Последовательность { x 2 n } сильно сходится к (
P а последовательность х2n+1 сходится к (
P В более общем случае следует положить k
=
inf
{
j
: ||
P и во всех последовательностях, рассмотренных выше, вместо индекса 1 подставить k
.
С целью ускорения сходимости процесса можно исходить из оператора Т
– Заключение В данной курсовой работе были рассмотрены линейный оператор, спектральная теория операторов и, в частности, спектральная теория компактных операторов, показано решение некоторых задач.Наиболее изученным классом теории операторов является теория компактных операторов, но, не смотря на это, остаётся пространство для исследования и изучения более глубокого. Решение ряда важных задач спектральной теории связано с теорией аналитических функций. Дело в том, что основные объекты, характеризующие спектральную задачу для оператора, такие как резольвента, собственные значения оператора и другие, являются аналитическими функциями спектрального параметра в определённых областях. На мой взгляд данная курсовая работа будет интересна всем, кто интересуется математикой. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ1. Ахнезер, М.Н., Глазман И.Н. Теория линейных операторов в гильбертовом пространстве/ М.Н. Ахнезер, И.Н. Глазман. – Киев: Виша школа, 1977. – 336 с. 2. Балакришнан, A.(BalakrishnanA.V.). Slochaslic Differential system/ A.V. Balakrishnan. – N.-Y.: Springer-Verlag, 1960. – 451 с. 3. Балакришнан, A.(Balakrishnan A.V.).Communication theory/ A.V. Balakrishnan. – N.-Y.: McGraw-Hill, 1968. – 432 с. 4. Блум, Е.(Blum E.K.). Numerical Analysis and Computation. Theory and Placlice/ Е. Блум. N.-Y.:Addison Wesley. 1972.–274 c. 5. Данфорд, Н. Линейные операторы/ Н. Данфорд, Дж. Шварц.– М.: Наука, 1966.– 386 с. 6. Канторович, Л.В. Функциональный анализ/ Л.В. Канторович, Акилов Г.П. – М.: Наука, 1977.– 231 с. 7. Люстерник, Л.А. Элементы функционального анализа/. Л.А. Люстерник, В. И. Соболев. – М.: Наука, 1965. – 496 с. 8. Люстерник, Л.А. Топология функциональных пространств и вариационное исчисление в целом/. Л.А. Люстерник, В. И. – М.: Наука, 1961. – 442 с. 9. Садовничий, В. А. Теория операторов/ В. А. Садовничий. – М.: Издательский дом «Дрофа», 2004. – 816 с. 10. Халмош, П. (Halmos P.) Introduction to Hilbert Space Theory/ П. Халмош. – .N-Y: Chelsea Publishing Co., 1951. – 480 с. |
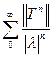 (2.2)
(2.2) (2.11)
(2.11) (2.12)
(2.12) (2.13)
(2.13)
 (2.14)
(2.14) (2.15)
(2.15)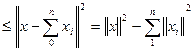 , потому ряд
, потому ряд 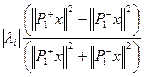 .
.