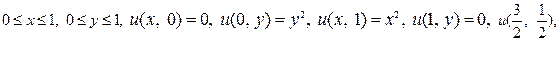Реферат: Решение задачи Дирихле методом Монте-Карло
|
Название: Решение задачи Дирихле методом Монте-Карло Раздел: Рефераты по математике Тип: реферат | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Введение Для сложных математических моделей аналитические решения удаётся получить сравнительно редко. Поэтому среди приближённых математических методов основными методами решения задач являются численные. Эти методы позволяют добиться хорошего качественного и количественного описания исследуемого процесса или явления. Задача Дирихле может быть сформулирована следующим образом: найти функцию, непрерывную в данной замкнутой области Цель данной работы рассмотреть решение задачи Дирихле для уравнения Лапласа и уравнения Пуассона методом Монте-Карло на основе метода сеток. Применяя метод сеток для решения краевых задач, прежде всего появляется задача замены дифференциальных уравнений разностными уравнениями – заданное дифференциальное уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным уравнением. Идея метода сеток восходит еще к Эйлеру. Однако практическое использование метода наталкивалось на серьезные трудности, так как получение достаточно точного решения краевой задачи приводило к системам алгебраических уравнений, на решение которых при ручном счете требовались затраты времени. Положение резко изменилось с появлением быстродействующих электронных вычислительных машин. Методами Монте-Карло называются численные методы решения математических задач при помощи моделирования случайных величин и статистической оценки их характеристик. В данной работе приведено два метода решения задачи Дирихле для уравнения Лапласа с использованием методом Монте-Карло, и на основании одного из них приведена программа его реализующая. 1. Метод Монте-Карло Общепринятого определения методов Монте-Карло пока нет. Назовем методами Монте-Карло численные методы решения математических задач при помощи моделирования случайных величин и статистической оценки их характеристик. При таком определении приходится к методам Монте-Карло причислить некоторые другие методы, как, например, стохастические приближения или случайный поиск, которые по традиции рассматриваются отдельно. Однако специалисты, занимающиеся этими вопросами, нередко сами называют свои приемы методами Монте-Карло. В то же время в определении подчеркивается что: а) речь идет о численных методах (и конкурировать они могут с классическими численными методами, а не с аналитическими методами решения задач); б) решать методами Монте-Карло можно любые математические задачи (а не только задачи вероятностного происхождения, связанные со случайными величинами). Официальной датой рождения методов Монте-Карло считают 1949 год, когда появилась статья под заглавием «Метод Монте-Карло». Возникновение метода связывают обычно с именами Дж. Неймана, С. Улама, Н. Метрополиса, а также Г. Кана и Э. Ферми; все они в 40-х годах работали в Лос-Аламосе (США). Необходимо сразу же подчеркнуть, что теоретические основы методов Монте-Карло были известны значительно раньше. Более того, фактически такие методы не раз использовались для расчетов в математической статистике. Однако до появления электронных вычислительных машин (ЭВМ) методы Монте-Карло не могли стать универсальными численными методами, ибо моделирование случайных величин вручную – весьма трудоемкий процесс. Развитию методов Монте-Карло способствовало бурное развитие ЭВМ. Алгоритмы Монте-Карло (как правило, обладающие небольшой связностью) сравнительно легко программируются и позволяют рассчитывать многие задачи, недоступные для классических численных методов. Так как совершенствование ЭВМ продолжается, есть все основания ожидать дальнейшего развития методов Монте-Карло и дальнейшего расширения области их применения. Важнейший прием построения методов Монте-Карло – сведение задачи к расчету математических ожиданий. Более подробно: для того чтобы приближенно вычислить некоторую скалярную величину а, надо придумать такую случайную величину Пример. Требуется оценить объем Выберем параллелепипед то, очевидно,
В этом примере случайная величина
Легко видеть, что существует бесконечно много случайных величин 1) как выбрать удобную величину 2) как находить значения Изучение этих вопросов и должно составить основное содержание практического курса методов Монте-Карло. Многие методы основаны на расчете математических ожиданий. Существуют методы случайного поиска (кроме простейшего) и стохастических приближений. Среди методов Монте-Карло можно выделить методы, в которых полностью воспроизводится модель рассчитываемого процесса. Такие методы иногда называют «физическими», хотя автору представляется более удачным другое название этих методов — имитационные. Имитация естественных процессов широко используется в самых различных областях науки, техники, экономики. Однако приемы имитации в каждой области свои, и подробно излагать их более целесообразно в специальных руководствах, а не в общем курсе методов Монте-Карло. 2. Задаче Дирихле для уравнения Лапласа 2.1 Основные сведения о задаче Дирихле для уравнения Лапласа Определение. Функция
Простейшим примером гармонической функции двух переменных является функция вида Задача Дирихле в иных терминах может быть сформулирована следующим образом: найти функцию, непрерывную в данной замкнутой области Если Свойcтво1 (принцип максимума). Гармоническая в ограниченной области функция, непрерывная в замкнутой области Доказательство. Пусть Составим вспомогательную функцию
где
причем при
Следовательно, функция
Из соотношения
вытекает, что по крайней мере одна из производных Аналогично доказывается, что Следствие. Пусть функция
где Замечание. Можно доказать более сильное утверждение, что гармоническая в ограниченной и замкнутой области Свойство II (единственность решения задачи Дирихле). Задача Дирихле для замкнутой и ограниченной области может иметь лишь единственное решение, т. е. не существует двух непрерывных гармонических функций в замкнутой ограниченной области Доказательство. Допустим, что две функции
Очевидно, что на Замечание. Из свойства II не следует, что задача Дирихле для ограниченной замкнутой области Можно доказать, что если область Свойство III (корректность задачи Дирихле). Решение задачи Дирихле для замкнутой и ограниченной области непрерывно зависит от граничных данных. Доказательство. Допустим, что Пусть всюду на
где Рассмотрим гармоническую функцию
На границе
Так как
т. е. Таким образом, для задачи Дирихле требование корректности выполнено при 2.2 Решение задачи Дирихле для уравнения Лапласа методом сеток Идея метода сеток (или, иначе, метода конечных разностей) для приближенного решения краевых задач для двумерных дифференциальных уравнений заключается в следующем: 1. в плоскостной задаче 2. заданное дифференциальное уравнение заменяется в узлах построенной сетки соответствующим конечно-разностным уравнением; 3. на основании граничных условий устанавливаются значения искомого решения в граничных узлах области Решив полученную систему конечно-разностных уравнений, для чего, вообще говоря, нужно решить алгебраическую систему с большим числом неизвестных, мы найдем значения искомой функции в узлах сетки, т. е. будем иметь численное решение задачи. Выбор сеточной области производится в зависимости от конкретной задачи, но во всех случаях контур Сеточная область может состоять из квадратных, прямоугольных, треугольных и других клеток. От выбора основного размера клетки Обычно задача решается сначала при большом значении Идея метода сеток восходит еще к Эйлеру. Однако практическое использование этого метода наталкивалось на серьезные трудности, так как получение с его помощью достаточно точного решения краевой задачи обычно приводило к системам алгебраических уравнений, на решение которых при ручном счете требовались затраты времени. Положение резко изменилось с появлением быстродействующих электронных вычислительных машин. Метод сеток допускает удобную реализацию на электронных счетных машинах, так как его применении сводится к повторяемости однородных циклов. В настоящее время метод сеток является одним из наиболее эффективных методов решения линейных, а также нелинейных задач математической физики. Покажем применение метода сеток для построения решения задачи Дирихле
где Выбрав шаг
с таким расчетом, чтобы узлы Точки (узлы) Граничный узел сетки Относительно сетки Значение искомой функции
где В граничных узлах первого рода
где Система (2) является неоднородной линейной системой, причем число неизвестных (т. е. число внутренних узлов сетки) равно числу уравнений. Система (2) всегда совместна и имеет единственное решение. Чтобы доказать это, достаточно убедиться в том, что соответствующая однородная система, очевидно, формально может быть записана в виде системы (2), с той лишь разницей, что значение функции Однородная система (2) всегда совместна, так как эта система имеет тривиальное решение
для всех узлов сетки
На основании системы (2) получаем
Учитывая неравенство (4), заключаем, что
Ни одно из последних четырех неравенств не является строгим, так как если бы это имело место, то, складывая все четыре неравенства и учитывая формулу (6), мы получили бы Поэтому
Проводя аналогичные рассуждения для точек
Таим образом, из цепи равенств (7) имеем Так, однородная система (2) не может иметь положительных решений. Аналогично доказывается, что эта система не может иметь отрицательных решений. Следовательно, Решив систему (2), получим приближенные значения искомой функции 2.3 Понятие о решение задачи Дирихле для уравнения Лапласа методом Монте-Карло Пусть на плоскости
Мы предполагаем, что сетка Представим себе частицу Если частица Равномерное случайное блуждание частицы на плоскости можно организовать с помощью равномерно распределенной последовательности одноразрядных случайных чисел, принимающих значения Случайные числа берутся из готовых таблиц или вырабатываются электронной машиной. Последний способ при работе на счетной машине предпочтительнее, так как он позволяет не загружать сильно память машины. Пусть в точках границы Г области G определена некоторая функция
Для краткости введем обозначение
Пусть
где суммирование распространяется на все точки
где Составим сумму
где точка
По формуле полной вероятности имеем
Отсюда, умножая обе части равенства (5) на граничные значения
Кроме того, в силу формулы (3) имеем
если точка Рассмотрим теперь задачу Дирихле об отыскании функции
Сравнивая формулы (8) с формулами (6), (7), мы усматриваем, что они совпадают с точностью до обозначений. Следовательно, искомые неизвестные
Формула (9) дает статистическую оценку величины Заметим, что с помощью формулы (9) можно непосредственно найти приближенное значение Интересно отметить, что вероятность
Построив такую функцию Грина, мы получаем возможность, применяя формулу (9), просто находить приближенное решение задачи Дирихле для области Недостатком рассмотренного варианта метода Монте-Карло для задачи Дирихле является слабая сходимость по вероятности при
к математическому ожиданию автоматически является случайным блужданием частицы, начинающимся в любой промежуточной точке траектории этой частицы. 2.4 Метод «блуждания» по сферам Укажем другой метод Монте-Карло для решения задачи Дирихле для уравнения Лапласа, не связанный с разностными уравнениями. Пусть задана ограниченная связная область Таким образом, Приведем теорему: если функция
то при каждом Доказательство. Придадим более точный смысл утверждению о произвольности радиуса
По теореме о среднем значении гармонической функции
Поэтому
При Построение траекторий рассмотренного типа в трехмерном случае иногда называют блужданием по сферам. Приведенную выше траекторию можно использовать для приближенного решения задачи Дирихле. Пусть на границе Фиксируем достаточно малую окрестность
Замети, что сходимость по вероятности
когда Если величины
(Доказательство этой теоремы легко получить, применяя к величине В нашем случае все Такой метод расчета Данный метод был предложен Дж. Брауном и обоснован М. Мюллером, который доказал, в частности, что вероятность того, что траектория
В ограниченной связной области
где Применяя метод сеток для решения краевых задач, прежде всего появляется задача замены дифференциальных уравнений разностными уравнениями. Аппроксимации дифференциального уравнения разностным заключается в том, что производные, входящие в дифференциальное уравнение, заменяются линейными комбинациями значений функции Предположим, что на границе
Задачу об отыскании решения уравнения
удовлетворяющего граничному условию, называют задачей Дирихле для уравнения Пуассона. Во внутреннем узле
которое перепишем в виде
В граничных узлах
Решение алгебраической системы при Перенумеруем все узлы, принадлежащие
Матрица этой системы имеет следующую структуру: внутреннему узлу с номером Один из методов решения системы (5) является метод Монте-Карло. Построим данный метод для расчета
Здесь Далее строим следующую цепь: 1) 2) если узел 3) если узел
где – номер первого выхода цепи на границу. В формуле (6) все Замечание. Если вместо граничных условий (2) заданы более сложные условия, например:
то уравнения (6) наряду с Если количество цепей достаточно велико, то решение задачи Дирихле в узле определяется по формуле
4. Прикладное применение метода Монте-Карло с использованием метода сеток для решения задачи Дирихле для уравнения Лапласа Пусть Выберем в квадрате сетку с шагом Для построения цепей необходимо воспользоваться таблицей случайных цифр (таблица 1, Приложение В). Если случайная цифра В таблице 2 (Приложение F) приведены 16 случайных цепей. В первой строке записаны использованные случайные цифры, а в третьей – сама цепь (номера
Из эмпирической оценки дисперсии
следует, что вероятная ошибка Точное решение рассмотренной задачи Приведенный здесь метод позволяет вычислять решения разностных уравнений, аппроксимирующих дифференциальные уравнения. 5. Математическое обоснование решения задачи Дирихле для уравнения Пуассона Найдем решение задачи Дирихле для уравнения Пуассона:
где Выберем в квадрате Рассчитываем вес вдоль цепи по правилу: пока цепь не попала на границу,
где – номер первого выхода цепи на границу. В формуле (6) все Итоговое значение функции получаем по формуле Заключение В данной работе были рассмотрены основные сведения, связанные с задачей Дирихле для уравнений Лапласа и Пуассона – определения, свойства и методы решения. Было приведено два метода решения данной задачи с помощью метода Монте-Карло – метод сеток и метод «блуждания» по сферам для уравнения Лапласа и метод сеток для уравнения Пуассона. Приведено математическое обоснование решения задачи Дирихле для уравнения Пуассона методом Монте-Карло с использованием метода сеток. В приложении приведена программа, написанная на BorlandPascal 7.0, реализующая данный метод с заданными исходными данными:
Также приведены рисунки, использованные в работе и таблицы для построения переходов, на основе генерации случайных цифр. Список использованной литературы 1. Соболь И. М. Численные методы Монте-Карло. – М.:Наука, 1973. – 312 с 2. Демидович Б. П., Марон И. А., Шувалова Э. З. Численные методы анализа. – М.:Наука, 1967. – 368 с. 3. Березин И. С., Жидков Н. П. Методы вычислений. – М.:Государственной литературы, 1959. – 602 с. 4. Бусленко Н. П., Шрейдер Ю. А. Метод статистических испытаний (Монте-Карло) и его реализация в цифровых машинах. – М.:Физматгиз, 1961. – 315 с. Приложения А. Сеточная область
(рис. 1) B. Таблица 1 (блуждание частицы на плоскости)
С. Ограниченная область
(рис. 2) D. Ограниченная область
(рис. 3) E. Единичный квадрат
(рис. 4) Единичный квадрат: в нем сетка с шагом F. Таблица 2 (случайные цепи)
G. Программа, реализующая решение задачи Дирихле методом Монте-Карло program kp; Uses crt; Const x=3/4; y=1/2; N=10; h=1/4; Var s1,f,s,u,u1,g,x_1,y_1: real; i : integer; procedure Loop; var f1,f2,f3,f4,f5:real; begin y_1:=y; x_1:=x; f:=0; repeat g:=random(10); writeln('g=',g); f1:=f; if (g=0) or (g=4) then begin x_1:= x_1 + h; f1:=f1-0.25*h*h*(x_1*x_1+y_1*y_1); f:=f1; end; f2:=f; if (g=1) or (g=5) then begin y_1:= y_1 + h; f2:=f2-0.25*h*h*(x_1*x_1+y_1*y_1); f:=f2; end; f3:=f; if (g=2) or (g=6) then begin x_1:= x_1 - h; f3:=f3-0.25*h*h*(x_1*x_1+y_1*y_1); f:=f3; end; f4:=f; if (g=3) or (g=7) then begin y_1:= y_1 - h; f4:=f4-0.25*h*h*(x_1*x_1+y_1*y_1); f:=f4; end; f5:=f; if (g=8) or (g=9) then begin y_1:=y_1; x_1:=x_1; f5:=f5-0.25*h*h*(x_1*x_1+y_1*y_1); f:=f5; end; until (x_1=0) or (x_1=1) or (y_1=0) or (y_1=1); if y_1=1 then s:=x_1*x_1; if (y_1=0) or (x_1=1) then s:=0; if x_1=0 then s:=y_1*y_1; s1:=s1+s; writeln('s=',s); writeln('s1=',s1); end; begin clrscr; randomize; u:=0; u1:=0; for i:=1 to N do begin Loop; writeln('f=',f); u:=u+f+s; writeln('u=',u); end; u1:=u/N; writeln('u1=',u1); writeln('press any key'); readkey; END. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
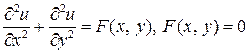 .
.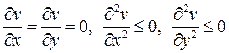 .
.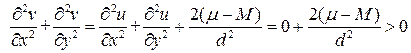
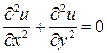 при
при 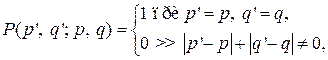 (3)
(3)
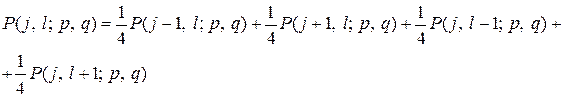 (5)
(5)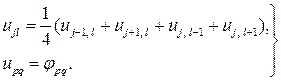 (8)
(8)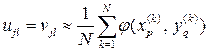 . (9)
. (9)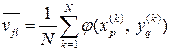
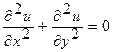 , (1)
, (1)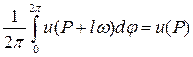 .
.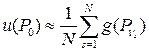 . (2)
. (2)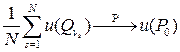 , (3)
, (3)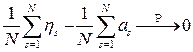
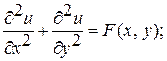 (1)
(1)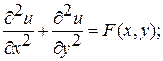 (3)
(3) 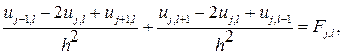 (4)
(4)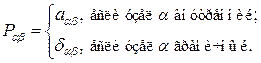
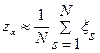 . (9)
. (9)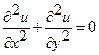 в единичном квадрате
в единичном квадрате 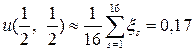 .
.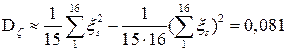
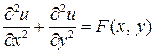 ,
,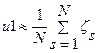 , где
, где