Введение
В современном обществе важную роль в механизме управления экономикой, торговлей выполняет новая наука – эконометрика
.
Сегодня деятельность в любой области экономики (управления, финансово-кредитной сфере, торговле, маркетинге, учете, аудите, внешнеторговых операциях) требует от специалиста применения современных методов работы, знания достижений мировой экономической мысли, понимания научного языка. Большинство новых методов основано на эконометрических моделях, концепциях, приемах. Без глубоких знаний эконометрики научиться их использовать невозможно.
Современные социально-экономические процессы и явления зависят от большого количества факторов, их определяющих. В связи с этим квалифицированному специалисту необходимо не только иметь четкие представления об основных направлениях развития экономики, но и уметь учитывать сложное взаимосвязанное многообразие факторов, оказывающих существенное влияние на изучаемый процесс. Такие исследования невозможно проводить без знания основ теории вероятностей, математической статистики, многомерных статистических методов и эконометрики, т.е. дисциплин, позволяющих исследователю разобраться в огромном количестве стохастической информации и среди множества различных вероятностных моделей выбрать единственную, наилучшим образом отражающую изучаемый процесс или явление.
Процесс перехода высшего образования России на мировые стандарты характеризуется интенсивным внедрением в учебные планы курсов микро- и макроэкономики. Эконометрика также начинает входить в учебные планы.
Данное учебное пособие предназначено для студентов экономических специальностей всех форм обучения. В краткой форме здесь представлены основные теоретические положения эконометрики с разобранными примерами практических их приложений. В главе 8 даны варианты контрольных заданий для проверки приобретенных студентами знаний, которые, по усмотрению преподавателя, могут быть выполнены как аналитически, так и на компьютере.
Эконометрика
– быстроразвивающаяся отрасль науки, цель которой состоит в том, чтобы придать количественные меры экономическим отношениям. Описание экономических систем математическими методами, или эконометрика, дает заключение о реальных объектах и связях по результатам выборочного обследования или моделирования. Вместе с тем, чтобы сделать вывод о том, какие из полученных результатов являются достоверными, а какие сомнительными или просто необоснованными, необходимо уметь оценивать их надежность и величину погрешности.
Зарождение эконометрики является следствием междисциплинарного подхода к изучению экономики. Эта наука возникла в результате взаимодействия и объединения трех компонент: экономической теории, статистических и математических методов. Впоследствии к ним присоединилось развитие вычислительной техники как условие развития эконометрики.
Таким образом, эконометрика
– это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов.
В результате статистико-математического анализа экономических отношений вырабатываются рекомендации по повседневным проблемам делового мира. При этом экономические показатели и процессы рассматриваются в общем случае как случайные величины и случайные процессы, требующие их статистической интерпретации. Основными элементами такого подхода являются понятия случайной величины и распределения ее вероятностей.
Становление и развитие эконометрического метода происходили на основе так называемой высшей статистики – на методах парной и множественной регрессии, парной, частной и множественной корреляции, выделения тренда и других компонент временного ряда, на статистическом оценивании. Исследование объективно существующих связей между явлениями – важнейшая задача теории статистики.
Социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. При изучении этих явлений необходимо выявлять основные причины, абстрагируясь от второстепенных.
Для изучения различных экономических явлений экономисты используют их прощенные формальные описания, называемые экономическими моделями.
Модель
– это условный образ объекта, построенный для упрощения его исследования. Математическая модель экономического объекта – это его отображение в виде совокупности уравнений, неравенств, логических отношений, графиков. Математические модели широко применяются в бизнесе, экономике, общественных науках, исследовании экономической активности и даже в исследовании политических процессов.
В настоящее время эконометрика располагает огромным разнообразием типов моделей – от больших макроэкономических моделей, включающих несколько сот, а иногда и тысяч уравнений, до малых коинтеграционных моделей, предназначенных для решения специфических проблем.
К основным задачам эконометрики можно отнести следующие:
· Построение эконометрических моделей, т.е. представление экономических моделей в математической форме, удобной для проведения эмпирического анализа. Данную проблему принято называть проблемой спецификации.
Зачастую она может быть решена несколькими способами.
· Оценка параметров построенной модели, делающих выбранную модель наиболее адекватной реальным данным. Это так называемый этап параметризации.
· Проверка качества найденных параметров модели и самой модели в целом. Иногда этап анализа называют этапом верификации.
· Использование построенных моделей для объяснения поведения исследуемых экономических показателей, прогнозирования и предсказания, а также для осмысленного проведения экономической политики.
Можно выделить три основных класса моделей, которые применяются для анализа и / или прогноза.
1. Модели временных рядов.
К этому классу относятся модели:
тренда: 
где T(
t)
– временной тренд заданного параметрического вида, 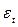 - случайная компонента; - случайная компонента;
сезонности:
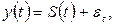
где S(
t)
– периодическая (сезонная) компонента, 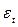 - случайная (стохастическая) компонента; - случайная (стохастическая) компонента;
тренда и сезонности:
 (аддитивная) или
(аддитивная) или
 (мультипликативная),
(мультипликативная),
где T(
t)
– временной тренд заданного параметрического вида, S(
t)
– периодическая (сезонная) компонента, 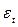 - случайная компонента. - случайная компонента.
К моделям временных рядов относится множество более сложных моделей, таких, как модели адаптивного прогноза, модели авторегрессии и скользящего среднего и др. Их общей чертой является то, что они объясняют поведение временного ряда, исходя только из его предыдущих значений. Такие модели могут применяться, например, для изучения и прогнозирования объема продаж авиабилетов, спроса на мороженое, краткосрочного прогноза процентных ставок и т.п.
2. Регрессионные модели с одним уравнением.
В таких моделях зависимая (объясняемая) переменная у
представляется в виде функции 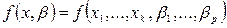 , где , где  - независимые (объясняющие) переменные, а - независимые (объясняющие) переменные, а  - параметры. В зависимости от вида функции - параметры. В зависимости от вида функции  модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т.п. модели делятся на линейные и нелинейные. Например, можно исследовать спрос на мороженое как функцию от времени, температуры воздуха, среднего уровня доходов или зависимость зарплаты от возраста, пола, уровня образования, стажа работы и т.п.
Область применения таких моделей, даже линейных, значительно шире, чем моделей временных рядов.
3. Системы одновременных уравнений.
Эти модели описываются системами уравнений. Системы могут состоять из тождеств и регрессионных уравнений, каждое из которых может, кроме объясняющих переменных, включать в себя также объясняемые переменные из других уравнений системы. Таким образом, имеется набор объясняемых переменных, связанных через уравнения системы. Примером может служить модель спроса и предложения. Системы одновременных уравнений требуют относительно более сложный математический аппарат. Они могут использоваться для моделей страновой экономики и др.
При моделировании экономических процессов мы встречаемся с двумя типами данных:
· пространственные данные;
· временные ряды.
Примером пространственных данных является, например, набор сведений (объем производства, количество работников, доход и др.) по разным фирмам в один и тот же момент времени (пространственный срез). Другим примером могут являться данные по курсам покупки/продажи наличной валюты в какой-то день по обменным пунктам города.
Примерами временных данных могут быть ежеквартальные данные по инфляции, средней заработной плате, национальному доходу, денежной эмиссии за последние годы или, например, ежедневный курс доллара США на ММВБ, цены фьючерсных контрактов на поставку доллара США (ММБ) и котировки ГКО (ММВБ) за два последних года.
Отличительной чертой временных данных является то, что они естественным образом упорядочены по времени, кроме того наблюдения в близкие моменты времени часто бывают зависимыми.
Процесс эконометрического моделирования происходит в течение нескольких этапов. В основе первого этапа
статистического изучения связей лежит качественный анализ явления, связанный с анализом его природы методами экономической теории, социологии, конкретной экономики. Второй этап
– построение модели связи. Он базируется на методах статистики: группировки, средних величин, таблиц и т.д. Третий этап
– интерпретация результатов. Он вновь связан с качественными особенностями изучаемого явления.
Существует множество методов изучения связей, выбор конкретного из которых зависит от цели исследования и от поставленной задачи. Связи между признаками и явлениями классифицируются по ряду оснований. Признаки по их значению для изучения взаимосвязи делятся на два класса:
1. Факторные (факторы)
– это признаки, обусловливающие изменение других, связанных с ними признаков.
2. Результативные
– это признаки, изменяющиеся под действием факторных признаков.
Связи между явлениями и их признаками классифицируются по степени тесноты, по направлению
(выделяют прямую
и обратную
связь), по аналитическому выражению
(выделяют прямолинейные
– или просто линейные
– и нелинейные
- или криволинейные
).
Для выявления наличия связи, ее характера и направления используются следующие методы: метод приведения параллельных данных
(основан на сопоставлении двух или нескольких рядов статистических величин, что позволяет установить наличие связи и получить представление о ее характере), аналитических группировок, графический, корреляции и регрессии.
Парная регрессия и корреляция в эконометрических исследованиях.
Парная регрессия
– уравнение связи двух переменных y
и x
:

где y
– зависимая переменная (результативный признак);
x
– независимая, объясняющая переменная (признак-фактор).
Различают линейные
и нелинейные
регрессии. Линейная регрессия
:
y
=
a
+
bx
+
e
.
Нелинейные регрессии
делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нелинейные по оцениваемым параметрам.
Регрессии, нелинейные по объясняющим переменным:
· полиномы разных степеней y
=
a
+
b
1
x
+
b
2
x
2
+
b
3
x
3
+
e
;
· равносторонняя гипербола   . .
Регрессии, нелинейные по оцениваемым параметрам:
· степенная y
=
a
×
xb
×
e
;
· показательная y
=
a
×
bx
×
e;
· экспоненциальная y
=
e
a
+
b
×
x
×
e
.
Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метод наименьших квадратов
(МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y
от теоретических  минимальна, т.е. минимальна, т.е.
 . .
Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно a
и b
:
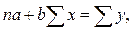

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:  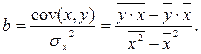
Тесноту связи изучаемых явлений оценивает линейный коэффициент парной корреляции
r
xy
для линейной регрессии (-1
£
rxy
£1
):

и индекс корреляции
ρ
xy
– для линейной регрессии (0
£
ρ
xy
£1
):

Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.
Средняя ошибка аппроксимации
– среднее отклонение расчетных значений от фактических:  Допустимый предел значений Допустимый предел значений 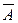 – не более 8-10%. – не более 8-10%.
Средний коэффициент эластичности
 показывает, на сколько процентов в среднем по совокупности изменится результат y
от своей средней величины при изменении фактора x
на 1% от своего среднего значения: показывает, на сколько процентов в среднем по совокупности изменится результат y
от своей средней величины при изменении фактора x
на 1% от своего среднего значения:
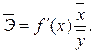
Задача дисперсионного анализа
состоит в анализе дисперсии зависимой переменной: 
где  - общая сумма квадратов отклонений; - общая сумма квадратов отклонений;
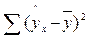 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»); - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
 - остаточная сумма квадратов отклонений. - остаточная сумма квадратов отклонений.
Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака y
характеризует коэффициент (индекс) детерминации
R
2
: 
Коэффициент детерминации – квадрат коэффициента или индекса корреляции.
F-тест
– оценивание качества уравнения регрессии – состоит в проверке гипотезы H
0
о статистической незначимости уравнения регрессии
и показателя тесноты связи
. Для этого выполняется сравнение фактического F
факт
и критического (табличного) F
табл
значений F-критерия Фишера
. F
факт
определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
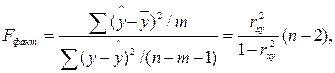
где n –
число единиц совокупности; m –
число параметров при переменныхx
.
F
табл
– это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости a
. Уровень значимости a
– вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно a
принимается равной 0,05 или 0,01.
Если F
табл
<
F
факт
, то H
0
– гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если F
табл
>
F
факт
, то H
0
– гипотеза не отклоняется и признается статистическая незначимость, надежность уравнения регрессии.
Для оценки статистической значимости коэффициентов регрессии и корреляции
рассчитываются t-критерий Стьюдента
и доверительные интервалы
каждого из показателей. Выдвигается гипотеза H
0
о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:
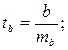 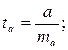 
Случайные ошибки
параметров линейной регрессии и коэффициента корреляции определяются по формулам: 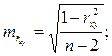
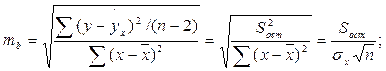
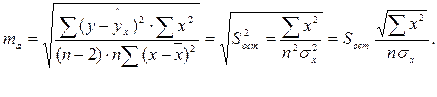
Если t
табл
<
t
фак
, то H
0
отклоняется, т.е. a
,b
и r
xy
не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора x
. Если t
табл
>
t
фак
, гипотеза H
0
не отклоняется и признается случайная природа формирования a
,b
или r
xy
.
Для расчета доверительного интервала определяем предельную ошибку
D
для каждого показателя: 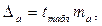 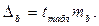
Формулы для расчета доверительных интервалов
имеют следующий вид:
 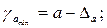  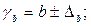  
Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.
Прогнозное значение
y
p
определяется путем подстановки в уравнение регрессии 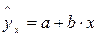 соответствующего (прогнозного) x
p
. Вычисляется средняя стандартная ошибка прогноза соответствующего (прогнозного) x
p
. Вычисляется средняя стандартная ошибка прогноза  где
где 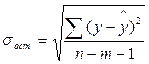 , и строится доверительный интервал прогноза
: , и строится доверительный интервал прогноза
:
  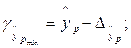 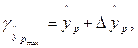 где где 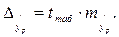
|
 .
.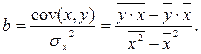


 Допустимый предел значений
Допустимый предел значений 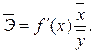

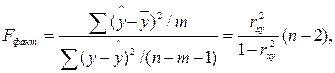
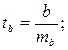
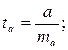

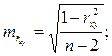
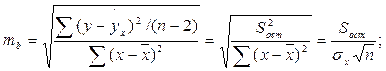
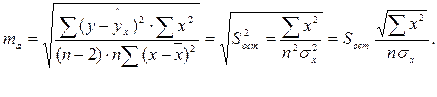
 где
где 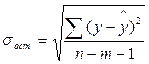 , и строится доверительный интервал прогноза
:
, и строится доверительный интервал прогноза
: