Экономико-математическая модель
Экономико-математическая модель – это выраженная в формально-математических терминах экономическая абстракция, логическая структура которой определяется как объективными свойствами предметами описания, так и субъективным целевым фактором исследования, для которого это описание предпринимается.
Между моделью и ее прототипом не может существовать взаимооднозначного соответствия, так как модель – это абстракция, связанная с обобщениями и потерей информации. Адекватность реальной действительности - основное требование ,предъявляемое к модели.
Конструктивно каждая математическая модель представляет собой совокупность взаимосвязанных математических зависимостей , отражающих определенные группы реальных экономических зависимостей.
Классифицируются экономико-математические модели по различным признакам, в том числе и по математическому инструменту, применяемому при моделировании.
Наиболее распространенными и эффективными математическими методами, которые нашли как теоретическое, так и практическое приложение в экономических исследованиях, являются: дифференциальное исчисление, математическая статистика, линейная алгебра, математическое программирование и другие.
Порядок построения экономико-математической модели
Для построения экономико-математической модели определяется объект исследования: экономика государства в целом, отрасль, предприятие, цех и т.п.
Формулируется цель исследования.
В рассматриваемом экономическом объекте выделяются структурные и функциональные элементы и выделяются наиболее существенные качественные характеристики этих элементов, влияющие на достижения поставленной цели.
Вводятся символические обозначения для учитываемых характеристик экономического объекта. Определяется, какие из них будут рассматриваться как зависимые величины, а какие как независимые.
Формализуются взаимосвязи между определенными параметрами модели, т.е. строится собственно экономико-математическая модель.
Проводятся расчеты по модели и анализируются результаты полученных расчетов.
Если результаты оказываются неудовлетворительными с точки зрения неадекватности отображения моделируемого процесса или явления ,то происходит возврат к одному из предшествующих пунктов и процесс повторяется.
Пример экономико-математической модели
Структуру предприятия удобно описывать организационной моделью, которая демонстрирует состав функциональных подразделений предприятия и связи их подчинения и взаимодействия.
При функциональной организационной структуре предприятие подразделяется на элементы, каждый из которых имеет свои задачи и обязанности. Характеристики и особенности того или иного подразделения соответствуют наиболее важным направлениям деятельности предприятия.
Функциональная организационная модель предприятия на примере ОАО швейная фабрика «Березка»:
Производство,
швейный цех
|
|
 Отдел конструкторов и дизайна
|
|
Такой вид организационной модели , как правило, встречается в крупных организациях, когда необходимо обеспечить слаженную совместную работу большого числа функциональных подразделений.
Объектом исследования будет являться швейная фабрика «Березка», целью исследования – оценка эффективности работы выпуска продукции. Более подробно для разрешения поставленной цели будем рассматривать функциональный и структурный элемент объекта - производство.
Наиболее существенные и качественные характеристики этого элемента представлены ниже в таблице 1 за временной период с мая 2005 по май 2006.
Для построения экономико-математической модели применен метод математической статистики
.
Расчеты по модели и анализ полученных результатов при использовании данного метода включает в себя этапы:
1.Графическое представление характеристик.
2.Предварительный статистический анализ(анализ данных по выборкам).
3.Корреляционный анализ данных.
4.Регрессионный анализ данных.
| сырье, м погонный
|
затраты на оплату труда,
тыс.руб.
|
материальные затраты, тыс.руб
|
амортизация, тыс.руб.
|
полная себестоимость, тыс.руб
|
| май
|
230 |
18729 |
21516 |
4642 |
78164 |
| июнь
|
303 |
7415 |
36225 |
1951 |
61068 |
| июль
|
102 |
7340 |
12064 |
1697 |
30564 |
| август
|
175 |
3156 |
18770 |
120 |
31750 |
| сентябрь
|
155 |
31854 |
32548 |
5364 |
93611 |
| октябрь
|
195 |
28224 |
23190 |
1693 |
77059 |
| ноябрь
|
112 |
19939 |
17061 |
2018 |
53794 |
| декабрь
|
185 |
26850 |
25530 |
2811 |
81330 |
| январь
|
98 |
18589 |
21042 |
4061 |
57179 |
| февраль
|
248 |
25728 |
35358 |
3718 |
89639 |
| март
|
111 |
14607 |
22426 |
2537 |
51239 |
| апрель
|
68 |
3920 |
13190 |
118 |
21689 |
| май
|
28 |
2347 |
5094 |
104 |
10510 |
Исходные данные ОАО швейная фабрика «Березка»
Таблица 1
Из исходных характеристик экономического объекта являются независимыми (Х1,Х2,Х3,Х4) или факторными признаками : сырье, затраты на оплату труда, материальные затраты, амортизация, а зависимой или результативным признаком (У) – полная себестоимость.
1. Графический анализ

Рисунок 1
2. Анализ данных по выборкам.
Предварительный статистический анализ представлен в таблице 2., в ходе которого по каждому параметру рассчитывались следующие статистические показатели: среднее значение показателя, стандартная ошибка, медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, ассиметричность, минимум, максимум, интервал, сумма, коэффициент вариации. Брался уровень надежности 95%.
Таблица 2 Результаты расчетов по этапу Статистический анализ
:
| СЫРЬЕ, М ПОГОННЫЙ
|
ЗАТРАТЫ НА ОПЛАТУ ТРУДА, Т.РУБ.
|
| Среднее |
154,6153846 |
Среднее |
16053,69231 |
| Стандартная ошибка |
21,57531188 |
Стандартная ошибка |
2876,404897 |
| Медиана |
155 |
Медиана |
18589 |
| Мода |
#Н/Д |
Мода |
#Н/Д |
| Стандартное отклонение |
77,79089328 |
Стандартное отклонение |
10371,02535 |
| Дисперсия выборки |
6051,423077 |
Дисперсия выборки |
107558166,7 |
| Эксцесс |
-0,406977947 |
Эксцесс |
-1,508916139 |
| Асимметричность |
0,302343811 |
Асимметричность |
0,016663109 |
| Интервал |
275 |
Интервал |
29507 |
| Минимум |
28 |
Минимум |
2347 |
| Максимум |
303 |
Максимум |
31854 |
| Сумма |
2010 |
Сумма |
208698 |
| Уровень надежности 95,0% |
47,00856628 |
Уровень надежности 95,0% |
6267,147886 |
| Коэффициент вариации V,% |
50,31251804 |
Коэффициент вариации V,% |
64,60211861 |
| МАТЕРИАЛЬНЫЕ ЗАТРАТЫ, Т.РУБ.
|
АМОРТИЗАЦИЯ,
Т.РУБ.
|
ПОЛНАЯ СЕБЕСТОИМОСТЬ,Т.РУБ.
|
| Среднее |
21847,23077 |
Среднее |
2371,846154 |
Среднее |
56738,15385 |
| Стандартная ошибка |
2536,823476 |
Стандартная ошибка |
477,0664476 |
Стандартная ошибка |
7447,106319 |
| Медиана |
21516 |
Медиана |
2018 |
Медиана |
57179 |
| Мода |
#Н/Д |
Мода |
#Н/Д |
Мода |
#Н/Д |
| Стандартное отклонение |
9146,647119 |
Стандартное отклонение |
1720,087539 |
Стандартное отклонение |
26850,92369 |
| Дисперсия выборки |
83661153,53 |
Дисперсия выборки |
2958701,141 |
Дисперсия выборки |
720972102,8 |
| Эксцесс |
-0,31202086 |
Эксцесс |
-0,830489026 |
Эксцесс |
-1,088043769 |
| Асимметричность |
0,037275084 |
Асимметричность |
0,204463241 |
Асимметричность |
-0,288180418 |
| Интервал |
31131 |
Интервал |
5260 |
Интервал |
83101 |
| Минимум |
5094 |
Минимум |
104 |
Минимум |
10510 |
| Максимум |
36225 |
Максимум |
5364 |
Максимум |
93611 |
| Сумма |
284014 |
Сумма |
30834 |
Сумма |
737596 |
| Уровень надежности 95,0% |
5527,26353 |
Уровень надежности 95,0% |
1039,438496 |
Уровень надежности 95,0% |
16225,85077 |
| Коэффициент вариации V,% |
41,86639129 |
Коэффициент вариации V,% |
72,52104172 |
Коэффициент вариации V,% |
47,32428157 |
Расчет производился в оболочке «Excel», Сервис → Анализ данных → Описательная статистика.
Выводы:
стандартные отклонения выборок исходных данных по сравнению со значениями самих данных велики, т.е. разброс точек в выборках большой.
Отклонения максимальных и минимальных значений выборок от соответствующих медиан и среднего также велики. Это означает , что точки выборок расположены рассеяно.
Значения коэффициента вариации выборок позволяет судить об их неоднородности.
3. Корреляционный анализ данных.
На этом этапе осуществ
ляется парное сравнение выборки результирующего показателя с выборками показателей, которые согласно теоретической модели рассматриваются как факторные, а также проверяется степень коррелируемости факторных показателей. Для этих целей строят и анализируют матрицы парных линейных коэффициентов корреляции r, которые изменяются от -1 до 1. Анализ применим лишь в случае линейной зависимости между признаками. Чем ближе значения коэффициента корреляции к -1 или к 1, тем выше степень коррелируемости соответствующих случайных величин. Однако, при r, близких к 1 или -1, регрессионные связи между соответствующими величинами устанавливаться не могут, так как эта ситуация означает фактически функциональную взаимосвязь показателей.
Значимость (существенность) линейного коэффициента корреляции проверяют на основе t-критерия Стьюдента. При этом выдвигается и проверяется нулевая гипотеза о равенстве коэффициента нулю, т.е. об отсутствии связи между х и у. Для этого определяется расчетное значение критерия:
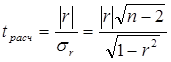 (1) (1)
где r – коэффициент корреляции,
n – число наблюденеий,
σr
– среднее квадратическое отклонение кэффициента корреляции.
и сопоставляется с tтабличное
с заданными параметрами (уровнем значимости α, принимается обычно за 0,05, и числом степеней свободы υ = n – 2, где n – число наблюдений).
Если tрасчетное
› tтабличное
, то нулевая гипотеза отвергается и линейный коэффициент считается значимым, а связь между х и у – существенной, если же неравенство обратное, то связь между х и у отсутствует.
Вообще говоря, отсутствие корреляционной связи между факторным признаками и наличие тесной связи (значение парных коэффициентов корреляции  )между результативным и факторными признаками – условие включения этих факторных признаков в регрессионную модель. )между результативным и факторными признаками – условие включения этих факторных признаков в регрессионную модель.
Кроме того, при построении модели регрессии необходимо учитывать проблему мультиколлениарности (тесной зависимости между факторными признаками), которая существенно искажает результаты исследования.
Одним из индикаторов определения наличия мультиколлинеарности между факторными
признаками является превышение величины парного коэффициента корреляции 0,8 (r ≤ 0,8).
| сырье,м погонный
|
затраты на заработную плату,т.руб.
|
материальные затраты,
тыс.руб
|
амортизация,
тыс.руб.
|
полная себесто-
имость,
тыс.руб
|
| сырье,м погонный
|
1 |
| затраты на заработную плату,т.руб.
|
0,349630305 |
1 |
материальные затраты,
тыс.руб
|
0,830118488 |
0,587647564 |
1 |
амортизация,
тыс.руб.
|
0,377214053 |
0,759164207 |
0,612169366 |
1 |
полная себестоимость,
тыс.руб
|
0,678604269 |
0,909886866 |
0,825715323 |
0,8247215 |
1 |
Таблица 3
Для определения наличия мультиколлениарности и устранения мультиколлениарных признаков была построена и проанализирована матрица парных коэффициентов корреляции, см. таблица 3.
Матрица парных коэффициентов корреляции
Расчет производился в оболочке «Excel», Сервис → Анализ данных → Корреляция.
Из таблицы 3 видно, что между факторными признаками Сырье и Материальные затраты коэффициент корреляции больше 0,8. Для устранения мультиколлинеарности необходимо исключить из корреляционной модели один из этих признаков, расчеты приведены в таблицах 4 и 5.
Матрица парных коэффициентов корреляции для модели без «Материальных затрат»
| сырье, м погонный
|
затраты на оплату труда,
тыс.руб.
|
амортизация,
тыс.руб.
|
полная себестоимость,
тыс.руб
|
| сырье, м погонный
|
1 |
| затраты на оплату труда, тыс.руб.
|
0,349630305 |
1 |
| амортизация, тыс.руб.
|
0,377214053 |
0,759164207 |
1 |
| полная себестоимость, тыс.руб
|
0,678604269 |
0,909886866 |
0,824721504 |
1 |
Таблица 4
Матрица парных коэффициентов корреляции для модели без «Сырья»
затраты на оплату труда,
тыс.руб.
|
материальные затраты,
тыс.руб
|
амортизация,
тыс.руб.
|
полная себестоимость,
тыс.руб
|
| затраты на оплату труда ,тыс.руб.
|
1 |
| материальные затраты, тыс.руб
|
0,587647564 |
1 |
амортизация,
тыс.руб.
|
0,759164207 |
0,612169366 |
1 |
полная себестоимость,
тыс.руб
|
0,909886866 |
0,825715323 |
0,824721504 |
1 |
Таблица 5
В обеих моделях теперь отсутствует проблема мультиколлениарности, т.к. все парные коэффициенты между факторными признаками < 0,8.
Так как коэффициент корреляции r между результативным и факторными признаками больше > 0,3, то все признаки дальше участвуют в анализе.
Какую из этих двух модель необходимо выбрать покажет дальнейший анализ.
Для определения признаков рассчитали tрасчетное
и взяли tтабличное
,см. таблицы 6 и 7.
Матрица расчетных значений t – критерия Стьюдента
для модели без «Материальных затрат»
| сырье, м погонный
|
затраты на оплату труда, тыс.руб.
|
амортизация, тыс.руб.
|
полная себестоимость, тыс.руб
|
| сырье, м погонный
|
Затраты
на оплату труда,
тыс.руб.
|
1,237707018 |
амортизация,
тыс.руб.
|
1,350871631 |
3,868284073 |
| полная себестоимость, тыс.руб
|
3,064211348 |
7,274210595 |
4,836609752 |
| tтабличное
|
2,200985159 |
Таблица 6
Матрица расчетных значений t – критерия Стьюдента
для модели без «Сырья»
| затраты на оплату труда,тыс.руб.
|
материальные затраты, тыс.руб
|
амортизация, тыс.руб.
|
полная себестоимость
,тыс.руб
|
| затраты на оплату труда тыс.руб.
|
| материальные затраты, тыс.руб
|
2,408806699 |
амортизация,
тыс.руб.
|
3,868284073 |
2,567683844 |
полная себестоимость,
тыс.руб
|
7,274210595 |
4,854902951 |
4,836609752 |
| tтабличное
|
2,200985159 |
Таблица 7
Расчет производился в оболочке «Excel» вручную по формуле (1), tтабличное
рассчитывалось с помощью функции СТЬЮДРАСПОБР исходя из той же формулы.
Выводы:
в результате сравнения tрасчетное
и tтабличное
выяснилось, что с вероятностью 0,95 можно утверждать , что связь между результативным и факторными признаками является существенной (tрасчетное
› tтабличное
), неслучайной. Какую из этих двух модель лучше выбрать покажет дальнейший анализ.
4. Регрессионный анализ данных.
На этом этапе, используя метод наименьших квадратов, строится многофакторная регрессионная зависимость(уравнение регрессии) результирующего показателя от оставшейся после предшествующих шагов анализа факторных показателей.
Линейная модель ,содержащая независимые переменные только в первой степени, имеет вид:
 (2) (2)
где а0
– свободный член,
а1…
аn
– параметры уравнения (коэффициенты регрессии),
х1….
хn
– значения факторных признаков.
Параметры уравнения регрессии рассчитываются методом наименьших квадратов , при этом решается система нормальных уравнений с к+1 неизвестными.
Для измерения степени совокупности влияния отобранных факторов на результативный признак рассчитывают совокупный коэффициент детерминации R2
и совокупный коэффициент множественной корреляции R – общие показатели тесноты связи признаков. Пределы изменения : 0 ≤ R ≥ 1. Чем ближе R к 1 , тем точнее уравнение множественной линейной регрессии отражает реальную связь.
Проверка значимости моделей, построенных на основе уравнений регрессии, начинается с проверки значимости каждого коэффициента регрессии. Значимость коэффициента регрессии осуществляется с помощью t – критерия Стьюдента ( отношение коэффициента регрессии к его средней ошибке):
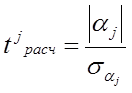 (3) (3)
Коэффициент регрессии считается статистически значимым , если tрасчетное
› tтабличное
с заданными параметрами (уровнем значимости α, = 0,05, и числом степеней свободы υ = n - к -1, где n – число наблюдений, к – число факторных признаков).
Проверка адекватности модели осуществляется с помощью F – критерия Фишера и величины средней ошибки аппроксимации, которая не должна превышать 12 – 15% . Если величина Fрасчетное
> Fтабличное
, то связь признается существенной. Fтабличное
находиться при заданном уровне значимости α = 0,05 и числе степеней свободы v1
=k и v2
= n-k-1. (4)
Модель без учета «Материальных затрат»
В таблице 8 сгенерированы результаты по регрессионной статистике.
| Регрессионная статистика
|
| Множественный R |
0,997434896 |
| R-квадрат |
0,994876372 |
| Нормированный R-квадрат |
0,993168496 |
| Стандартная ошибка |
2219,306976 |
| Наблюдения |
13 |
Таблица 8
Эти результаты соответствуют следующим статистическим показателям:
Множественный R – коэффициент корреляции R,
R-квадрат – коэффициент детерминации R2
;
В таблице 9 сгенерированы результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации R2
.
Таблица 9
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия |
3 |
8607337323 |
2869112441 |
582,5226438 |
1,2734E-10 |
| Остаток |
9 |
44327911,1 |
4925323,455 |
| Итого |
12 |
8651665234 |
Df – число степеней свободы, SS – сумма квадратов отклонений,
MS - дисперсия MS, F – расчетное значение F-критерия Фишера,
Значимость F – значение уровня значимости, соответствующее вычисленному F;
Коэффи
циенты
|
Стандарт
ная
ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
полная
себесто-
имость,
тыс.руб
|
2857,593011 |
1130,014906 |
2,528810014 |
0,094646561 |
603,5411613 |
6318,727183 |
сырье,
м погонный
|
132,3000047 |
8,941959918 |
14,79541464 |
1,27093E-07 |
112,071886 |
152,5281233 |
затраты
на оплату
труда,
тыс.руб.
|
1,586039072 |
0,095432478 |
16,61948958 |
4,61669E-08 |
1,370155809 |
1,801922334 |
амортизация,
тыс.руб.
|
3,357368468 |
0,582082818 |
5,76785358 |
0,000270158 |
2,040605653 |
4,674131282 |
В таблице 10 сгенерированы значения коэффициентов регрессии и их
статистические оценки.
Таблица 10
Коэффициенты – значения коэффициентов регрессии,
Стандартная ошибка – стандартные ошибки коэффициентов регрессии,
t – статистика – расчетные значения t – критерия Стьюдента, вычисляемые по формуле 2,
Р-значения – значения уровней значимости ,соответствующие вычисленным значениям t,
Нижние 95% и Верхние 95% - соответствующие границы доверительных интервалов для коэффициентов регрессии.
В таблице 11 сгенерированы предсказанные значения результирующего фактора Y и значения остатков. Последние вычисляются как разность между предсказанным и исходным значениям Y.
| Наблюдение
|
Предсказанное Y
|
Остатки
|
| 1 |
78576,42428 |
-412,4242814 |
| 2 |
61255,20002 |
-187,2000206 |
| 3 |
33691,17456 |
-3127,174561 |
| 4 |
31418,51735 |
331,4826465 |
| 5 |
91894,70678 |
1716,293221 |
| 6 |
79104,48549 |
-2045,485491 |
| 7 |
56074,39615 |
-2280,396148 |
| 8 |
79355,80571 |
1974,194293 |
| 9 |
58940,14712 |
-1761,147116 |
| 10 |
88956,30336 |
682,6966372 |
| 11 |
49227,81005 |
2011,189951 |
| 12 |
18467,43597 |
3221,564032 |
| 13 |
10633,59316 |
-123,5931632 |
Таблица 11
Расчет производился в оболочке «Excel», Сервис → Анализ данных → Регрессия.
tтабличное
рассчитывалось с помощью функции СТЬЮДРАСПОБР исходя из формулы (3).
Fтабличное
рассчитывалось с помощью функции FРАСПОБР исходя из формулы (4).
Модель без учета «Сырья»
| Регрессионная статистика
|
| Множественный R |
0,983232832 |
| R-квадрат |
0,966746802 |
| Нормированный R-квадрат |
0,955662403 |
| Стандартная ошибка |
5653,863353 |
| Наблюдения |
13 |
Таблица 12
| df
|
SS
|
MS
|
F
|
Значимость F
|
| Регрессия |
3 |
8363969696 |
2787989899 |
87,21688674 |
5,68904E-07 |
| Остаток |
9 |
287695537,3 |
31966170,81 |
| Итого |
12 |
8651665234 |
Таблица 13
Коэффи
циенты
|
Станда
ртная
ошибка
|
t-статистика
|
P-Значение
|
Нижние
95%
|
Верхние 95%
|
полная
себесто
имость,
тыс.руб
|
1992,888488 |
4236,311712 |
0,470430087 |
0,649239402 |
-7590,314376 |
11576,09135 |
затраты
на оплату
труда, тыс.руб.
|
1,430363491 |
0,248983274 |
5,744817576 |
0,000278107 |
0,867124195 |
1,993602788 |
матери
альные
затраты,
тыс.руб
|
1,187585684 |
0,232389908 |
5,11031521 |
0,000636233 |
0,661883189 |
1,713288179 |
аморти
зация,
тыс.руб.
|
2,461032929 |
1,536123969 |
1,602105675 |
0,143596048 |
-1,013920904 |
5,935986761 |
Таблица 14
| Наблюдение
|
Предсказанное Y
|
Остатки
|
| 1 |
65758,37475 |
12405,62525 |
| 2 |
60420,80042 |
647,1995839 |
| 3 |
30995,16308 |
-431,1630845 |
| 4 |
29093,4229 |
2656,577097 |
| 5 |
99410,20661 |
-5799,206609 |
| 6 |
74070,10843 |
2988,891574 |
| 7 |
55740,66995 |
-1946,669945 |
| 8 |
77635,1743 |
3694,825697 |
| 9 |
63565,34811 |
-6386,348112 |
| 10 |
89934,05543 |
-295,0554319 |
| 11 |
55762,64509 |
-4523,645092 |
| 12 |
23554,57043 |
-1865,57043 |
| 13 |
11655,4605 |
-1145,460501 |
Таблица 15
Все пояснения к таблицам , а также способ расчета, указаны в модели без учета «Материальных затрат» .
Перейдем к анализу сгенерированных таблиц обеих моделей.
Значение множественного коэффициента регрессии R в модели без учета «Материальных затрат» равно 0, 997, а в модели без учета «Сырья» равно 0,983. Это позволяет сделать вывод, что первая модель точнее отражает реальную связь.
При оценке значимости коэффициентов регрессии с помощью сравнения расчетного и табличного значений t – критерия Стьюдента стало очевидно, что следует выбрать модель «Материальных затрат».
В данной модели tрасчетное
найденных коэффициентов превышает tтабличное
(см. таблицу 10) t – критерия Стьюдента, что позволяет сделать вывод, что коэффициенты регрессии в уравнении являются значимыми.
Тогда как в модели без учета «Сырья» два коэффициента регрессии ниже tтабличное
( см. таблицу 14), что говорит об отсутствии их значимости.
Проверку адекватности модели осуществляем уже только с моделью без учета «Материальных затрат».
Значение средней ошибки аппроксимации не превышает 12-15 %, что хорошо видно на рисунке 2, так как разница между предсказанным и исходным результирующим фактором Y очень небольшая.
Рассчитанный уровень значимости (см. таблицу 9) равен 1,2734E-10 < 0,05, это подтверждает значимость R2
. Значение Fрасчетное
– критерия Фишера больше Fтабличное
, значит связь между признаками признается существенной.

Рисунок 2
Таким образом, получаем искомое уравнение регрессии:
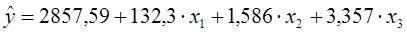
Выводы:
Выполнив данную работу по этапам, была построена экономико-математическая модель методом математической статистики на примере ОАО швейной фабрики «Березка». Модель имеет вид:
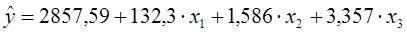 . .
Выбранные факторы Х1
,Х2
и Х3
существенно влияют на У, что подтверждает правильность их включения в построенную модель.
Так как коэффициент детерминации R2
значим, то это свидетельствует о существенности связи между рассматриваемыми признаками.
Отсюда следует, что построенная модель эффективна.
|