Министерство образования и науки Республики Казахстан
Восточно-Казахстанский государственный технический университет
им. Д. Серикбаева
Экономический анализ хозяйственной деятельности предприятий
Рабочая программа, задания и методические указания
по выполнению курсовой работы для студентов специальности 070640 "Финансы и кредит"
Усть-Каменогорск, 2003
УДК 658.1: 338.3 (075.8)
Екеева З.Ж., Садыкова А.Е. Экономический анализ хозяйственной деятельности предприятий: Рабочая программа, задания и методические указания по выполнению курсовой работы для студентов специальности 070640 (СПО) "Финансы и кредит" заочной формы обучения / ВКГТУ. - Усть-Каменогорск, 2003. - 31 с.
Методические указания содержат необходимые положения по организации курсовой работы и теоретические сведения по основным методам экономического анализа.
Цели изучения дисциплины
Переход к рыночной экономике требует от предприятий повышения эффективности производства, конкурентоспособности продукции и услуг на основе внедрения достижений научно-технического прогресса, эффективных форм хозяйствования и управления производством.
Важная роль в реализации этой задачи отводится экономическому анализу деятельности субъектов хозяйствования. С его помощью вырабатываются стратегия и тактика развития предприятия, обосновываются планы и управленческие решения, осуществляется контроль за их выполнением, выявляются резервы повышения эффективности производства, оцениваются результаты деятельности предприятия, его подразделений и работников.
Квалифицированный экономист, финансист, бухгалтер, аудитор должен хорошо владеть современными методами экономических исследований, методикой системного, комплексного экономического анализа, мастерством точного, своевременного, всестороннего анализа результатов хозяйственной деятельности.
Задачи дисциплины
Задачи анализа хозяйственной деятельности как научной дисциплины вытекает прежде всего из тех функций, которые он выполняет в системе других прикладных экономических наук. Таким образом, одними из основных функций анализа являются.
1.2.1 Изучение характера действия экономических законов, установление закономерностей и тенденций экономических явлений и процессов в конкретных условиях предприятия.
1.2.2 Научное обоснование текущих и перспективных планов.
1.2.3 Контроль за выполнением планов и управленческих решений, за экономным использованием ресурсов.
1.2.4 Поиск резервов повышения эффективности производства на основе изучения передового опыта и достижений науки и практики.
1.2.5 Оценка результатов деятельности предприятия выполнению планов, достигнутому уровню развития экономики, использованию имеющихся возможностей.
1.2.6 Разработка мероприятий по использованию выявленных резервов.
Содержание дисциплины
2.1 Метод и методика комплексного экономического анализа хозяйственной деятельности предприятий. Понятие АХД. Анализ и синтез как особенности человеческого мышления. Виды АХД, его роль. АХД как функция управления. Содержание АХД как науки, направленной на решение определенных задач. Функции анализа. Системный подход в АХД, главные особенности системного подхода. Характерные черты метода АХД. Методика АХД. Последовательность комплексного АХД. Способы АХД, их классификация. Роль показателей в комплексном анализе, характеристика содержания подсистем. Взаимосвязи между отдельными подсистемами. Разработка системы аналитических показателей, их классификация.
2.2 Способы обработки экономической информации в АХД. Способы сравнения в АХД. Сущность сравнения, типы сравнений и их цель. Многомерные сравнения в АХД. Задачи, возможности и направления использования многомерных сравнений в АХД. Алгоритм многомерных сравнений. Способы приведения показателей в сопоставимый вид. Условия сопоставимости показателей. Нейтрализация влияния стоимостных, объемных, качественных и структурных факторов. Использование относительных и средних величин в практике экономической и аналитической работы. Способы группировки информации. Алгоритм построения аналитических группировок. Использование балансового способа в АХД. Использование графического и табличного способов.
2.3 Методика факторного анализа. Взаимосвязь экономических явлений. Представление о факторном анализе. Типы факторного анализа, его основные задачи. Значение классификации факторов. Основные типы факторов. Понятие и отличие различных типов факторов в АХД. Необходимость и значение систематизации факторов. Основные способы систематизации факторов в детерминированном и стохастическом анализе. Сущность и значение моделирования, требования к нему. Основные типы факторных детерминированных моделей. Способы преобразования факторных моделей. Правила моделирования.
2.4 Методика функционально-стоимостного анализа (ФСА). История развития ФСА. Сущность функционального подхода к анализу объекта. Виды потребительских функций объекта. Алгоритм ФСА. Особенности и задачи ФСА. Ранняя диагностика, приоритетность, оптимальная детализация, выделение ведущего звена - главные принципы ФСА. Другие принципы ФСА. Этапы выполнения исследований по ФСА. Особенности организации исследований по ФСА в СНГ и ведущих странах Запада. Проблемы дальнейшего развития исследований по методике и организации ФСА.
2.5 Методика обоснования управленческих решений на основе маржинального анализа. Понятие маржинального анализа, его возможности, основные этапы и условия проведения. Методы определения суммы постоянных и переменных издержек. Понятие и значение показателей безубыточного объема продаж и зоны безопасности предприятия. Понятие и порядок определения критической величины постоянных расходов и уровня цены. Порядок обоснования объема продаж, который дает одинаковую прибыль по разным вариантам управленческих решений. Аналитическая оценка решения о принятии дополнительного заказа по цене ниже себестоимости продукции. Обоснование варианта цены на новое изделие. Обоснование решения "производить или покупать". Выбор варианта технологии производства. Выбор решения с учетом ограничения на ресурсы.
3. Цель, задачи выполнения курсовой работы
Цель курсовой работы - получить навыки по анализу производственно-хозяйственной деятельности фирмы (предприятия).
Основными задачами курсовой работы являются:
закрепление и углубление знаний студентов по курсу "Экономический анализ хозяйственной деятельности предприятий".
приобретение практических навыков при расчете основных экономических показателей деятельности предприятия.
применение ЭВМ для обработки экономической информации.
приобретение практических навыков и умений при использовании учебной, справочно-нормативной литературой.
Курсовая работа состоит из следующих заданий:
Задание первое - корреляционно-регрессионный анализ для определения влияния факторных показателей на результативный показатель.
Задание второе - анализ хозяйственной деятельности предприятия:
анализ производства и реализации промышленной продукции.
анализ использования ресурсов предприятия.
анализ прибыли и рентабельности.
4. Порядок выполнения курсовой работы
Курсовая работа по курсу "Экономический анализ хозяйственной деятельности предприятия" представляет собой самостоятельно выполненную студентом и представленную в письменном виде расчетную работу.
Курсовая работа состоит, как правило, из введения, расчетной части, заключения, списка использованной литературы.
Во введении необходимо показать роль анализа хозяйственной деятельности, как одной из основных функций менеджмента предприятия.
Расчетная часть состоит из двух отдельных заданий, к каждому из которых необходимо выбрать исходные данные по соответствующей методике (пункты 4.1 и 4.2). При выполнении заданий необходимо руководствоваться следующими требованиями:
в начале работы должен быть указан номер варианта задания
обязательно приводятся исходные данные
расчеты должны быть развернутыми, их следует сопровождать необходимыми формулами и краткими пояснениями. Если имеется несколько методов расчета, надо применить наиболее рациональный из них.
в процессе выполнения заданий нужно проверять производимые расчеты, пользуясь взаимосвязью между исчисляемыми показателями и обращая внимание на экономическое содержание последних
все расчеты должны сопровождаться выводами, что и является результатом аналитической работы
в заключении даются краткие выводы по результатам расчетов 1 и 2 задания, а также предложения, основанные на данных расчетах.
4.1 Выбор варианта к заданию 1
Исходные данные по вариантам студент получает из таблицы 1. Данные столбца № 2 изменяются вследствие прибавления к исходному числу последней цифры номера зачетной книжки.
Таблица 1 - Исходные данные к заданию 1
| № предприятия |
Прибыль от реали-зации, тыс. тг. |
Объем релизованной прод., млн. тг. |
Объем валовой продукции млн. тг. |
Среднегодовая стои-мость ос-новных и оборотных фондов, млн. тг. |
Себестоимость всей товарной продукции млн. тг. |
Фонд заработ-ной платы рабочих, тыс. тг. |
Затраты на 1 тг.
Товарной продукции тис. тг.
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1 |
41 |
1,7 |
1,66 |
0,27 |
1,5 |
285,3 |
97,7 |
| 2 |
75 |
2,2 |
2,2 |
0,55 |
2,1 |
275,6 |
97,3 |
| 3 |
82 |
1,3 |
1,4 |
0,47 |
1,1 |
253,3 |
94,6 |
| 4 |
106 |
18,9 |
19,9 |
4,96 |
18,7 |
3673,2 |
99,0 |
| 5 |
181 |
8,8 |
8,9 |
1,63 |
8,6 |
1224,0 |
97,7 |
| 6 |
215 |
3,9 |
4,0 |
0,91 |
3,6 |
734,9 |
94,6 |
| 7 |
254 |
4,3 |
4,2 |
0,74 |
4,0 |
753,2 |
93,7 |
| 8 |
262 |
1,6 |
1,7 |
0, 19 |
1,1 |
267,4 |
82,0 |
| 9 |
395 |
11,7 |
11,8 |
1,61 |
11,3 |
1675,6 |
96,0 |
| 10 |
512 |
2,2 |
2,2 |
0,49 |
1,7 |
299,3 |
77,5 |
| 11 |
526 |
4,8 |
4,9 |
1,12 |
4,3 |
956,3 |
89,5 |
| 12 |
558 |
6,5 |
6,6 |
2,18 |
5,7 |
1438,8 |
90,3 |
| 13 |
575 |
14,9 |
15,0 |
2,43 |
14,3 |
2000,9 |
85,3 |
| 14 |
602 |
9,5 |
9,6 |
1,78 |
8,8 |
1056,6 |
93,2 |
| 15 |
664 |
5,9 |
5,9 |
0,56 |
5,1 |
495,8 |
88,7 |
| 16 |
789 |
16,0 |
16,7 |
0,78 |
15,2 |
1383,3 |
94,7 |
| 17 |
902 |
22,3 |
22,1 |
2,72 |
19,2 |
2805,0 |
95,7 |
| 18 |
909 |
8,0 |
7,9 |
2,60 |
7,1 |
1202,0 |
90,4 |
| 19 |
967 |
26,0 |
26,1 |
7,00 |
24,8 |
4161,8 |
96,2 |
| 20 |
998 |
7,5 |
7,5 |
0,30 |
6,4 |
633,2 |
86,2 |
4.2 Выбор варианта к заданию 2.
Значения таблицы 2 "Исходные данные для анализа хозяйственной деятельности предприятия" изменяются в соответствии с коэффициентом, который выбирается из таблицы 3 по двум последним цифрам зачетной книжки
Таблица 2 - Исходные данные для анализа хозяйственной деятельности предприятия
| Показатели |
Единица измерен. |
Отчетный год |
| план |
Факт |
| 1 Производство продукции, всего |
Тыс. шт.
Тыс. тг.
|
| В т. ч. Изделие 1 |
Тыс. шт.
Тыс. тг.
|
20,98
|
20,18 |
| Изделие 2 |
Тыс. шт.
Тыс. тг.
|
18,66 |
18,51 |
| Изделие 3 |
Тыс. шт.
Тыс. тг.
|
13,87 |
13,76 |
| Изделие 4 |
Тыс. шт.
Тыс. тг.
|
22,84 |
22,99 |
| 2 Реализация продукции, всего |
Тыс. шт.
Тыс. тг.
|
| В т. ч. Изделие 1 |
Тыс. шт.
Тыс. тг.
|
19,46 |
119,8 |
| Изделие 2 |
Тыс. шт.
Тыс. тг.
|
18,66 |
14,21 |
| Изделие 3 |
Тыс. шт.
Тыс. тг.
|
13,83 |
12,96 |
| Изделие 4 |
Тыс. шт.
Тыс. тг.
|
22,72 |
22,8 |
3 Число отработанных рабочими за год:
человеко-дней
человеко-часов
в том числе сверхурочно, чел-часов
|
146093
1144742
|
140714
1097569
6300
|
| 4 Среднегодовая численность рабочих |
чел |
596 |
612 |
| 5 Среднегодовая стоимость основных производственных фондов |
Тыс. тг. |
1404,33 |
1343,4 |
6 Нормы расхода материалов
в т. ч. Изделие 1
Изделие 2
Изделие 3
Изделие 4
|
Тг. /ед.
Тг. /ед.
Тг. /ед.
Тг. /ед.
Тг. /ед.
|
54
76
63
59
|
53
78
61
60
|
7 Стоимость материалов:
в т. ч. Изделие 1
Изделие 2
Изделие 3
Изделие 4
|
Тенге
Тенге
Тенге
Тенге
Тенге
|
65
173
113
109
|
66
172
112,3
107
|
| 8 Себестоимость единицы продукции |
Тенге |
188 |
185 |
9 Цена единицы изделия
Изделие 1
Изделие 2
Изделие 3
Изделие 4
|
Тенге
Тенге
Тенге
Тенге
|
В таблице 3 задан коэффициент, который изменяет только показатели пунктов: 1,2, 4, 5 таблицы 2. Здесь также задана плановая цена единицы изделия по видам (выделено курсивом), а распределение цен по видам изделий необходимо сделать исходя из стоимости материалов (изделие, которое изготавливается из самого дорогого материала будет иметь самую высокую цену, и так далее по убывающей). Цены по факту определяются умножением коэффициента на плановые цены.
 Таблица 3 - Коэффициент, изменяющий основные показатели, цены на продукцию (курсив) Таблица 3 - Коэффициент, изменяющий основные показатели, цены на продукцию (курсив)
Предп.
По
след.
цифрв
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 0 |
0,95
240
171
143
194
|
1,32
257
231
183
160
|
1,04
279
249
180
193
|
1,39
284
165
247
200
|
1,12
226
256
296
278
|
1,35
126
181
185
278
|
0,98
269
176
152
235
|
1,1
297
255
125
159
|
0,99
300
290
187
179
|
1,31
123
167
210
262
|
| 1 |
1,37
233
190
289
169
|
1,14
255
177
219
241
|
1,47
244
251
290
144
|
1,07
291
156
265
142
|
1,04
242
203
165
163
|
1,14
180
266
121
282
|
1,23
120
146
194
129
|
0,81
138
241
291
178
|
1,45
136
266
259
137
|
1,07
249
244
239
281
|
| 2 |
1,15
220
150
262
197
|
1,3
226
239
209
210
|
0,91
276
177
133
287
|
0,94
169
208
209
260
|
1,27
289
250
268
255
|
0,92
257
225
205
192
|
1,03
286
281
260
213
|
1,33
220
177
168
243
|
1,25
229
191
152
246
|
0,98
113
138
259
256
|
| 3 |
1,46
142
300
231
129
|
0,94
200
185
191
260
|
1,03
233
264
204
252
|
1,21
148
285
121
124
|
0,82
251
215
183
120
|
1,08
245
140
294
126
|
0,9
272
143
153
132
|
0,89
183
123
249
122
|
0,83
150
245
276
165
|
1,42
126
290
218
166
|
| 4 |
1,02
116
273
198
125
|
1,38
131
184
170
154
|
1,15
230
126
142
113
|
1, 13
241
174
258
162
|
1,05
198
176
254
150
|
1,12
195
152
284
119
|
1,06
248
262
137
248
|
1,43
155
147
291
151
|
1,17
114
285
248
174
|
1,22
145
233
147
160
|
| 5 |
0,83
163
182
245
117
|
1,18
168
121
129
174
|
1,01
221
125
213
144
|
1,37
171
164
216
126
|
1,15
280
125
188
228
|
0,84
260
173
267
134
|
1,34
276
221
145
141
|
1,26
203
151
261
262
|
1,06
248
158
291
205
|
0,87
117
279
170
173
|
| 6 |
1,12
232
217
256
150
|
1,4
267
258
121
191
|
1,49
299
118
288
269
|
1,2
241
161
211
143
|
1,36
185
268
147
231
|
1,11
125
241
226
238
|
1,14
239
172
273
157
|
1,18
158
280
110
222
|
1,32
191
174
246
220
|
1,01
240
171
143
194
|
| 7 |
0,93
257
231
183
160
|
0,96
279
249
180
193
|
0,91
284
165
296
278
|
1,11
226
256
247
200
|
1,13
276
177
133
287
|
1,24
169
208
209
260
|
1, 19
289
250
268
255
|
0,95
257
225
205
192
|
0,98
286
281
260
213
|
1,18
220
177
168
243
|
| 8 |
1,41
229
191
152
246
|
1,17
113
138
259
256
|
1,24
142
300
231
129
|
1,28
200
185
191
260
|
0,86
233
264
204
252
|
1,16
148
285
121
124
|
1,15
251
215
183
120
|
1,31
245
140
294
126
|
1,33
272
143
153
132
|
1,29
183
123
249
122
|
| 9 |
0,86
150
245
276
165
|
1,05
126
290
218
166
|
1,06
116
273
198
125
|
1,16
131
184
170
154
|
1,2
230
126
142
113
|
1,17
241
174
258
162
|
1,09
198
176
254
150
|
1,22
195
152
284
119
|
0,85
248
262
137
248
|
0,95
155
147
291
151
|
4.3 Указания к выполнению задания 1
Постройте многофакторную регрессионную модель, отражающую влияние приведенных факторов на величину рентабельности. Проведите предварительный качественный анализ исходных данных, определите вид уравнения регрессии, отберите факторы, имеющие наибольшее влияние на результативный признак. Рассчитайте множественный, частные и парные коэффициенты корреляции. Определите эластичность факторов. Проанализируйте полученные результаты. Построить диаграммы.
Распечатка подшивается в курсовую работу.
4.4 Указания к выполнению задания 2
4.4.1 Исходные данные для выполнения задания 2 сводятся в соответствующие таблицы.
4.4.2 Анализ производства и реализации промышленной продукции.
Таблица 4 - Исходные данные для анализа производства и реализации промышленной продукции
Вид
изделия
|
Ед. изме
Рения
|
Производство продукции |
Реализация продукции |
| план |
факт |
план |
факт |
| Изделие А |
Шт. тенге |
| Изделие Б |
Шт. тенге |
| … |
| …. |
Анализ производства и реализации продукции необходимо начать с оценки выполнения плана по ассортименту. Расчеты свести в таблицу 5.
Таблица 5 - Выполнение плана по ассортименту продукции
Вид
изделия
|
Объем производства
продукции в плановых ценах,
тыс. тг
|
Выполнение
плана,%
|
Объем продукции, зачтенный в
выполнение плана по ассортименту,
тыс. тг
|
| план |
факт |
Итоги анализа структуры товарной продукции сводятся в таблицу 6.
Таблица 6 - Анализ структуры товарной продукции
| Вид изделия |
Оптовая цена за единицу изделия, тенге |
Объем произв. продукции, тыс. шт |
Товарная продукция в ценах плана, тыс. тг. |
Изменение товарной продукции за счет структуры, тыс. тг. |
| план |
факт |
план |
фактический при плановой структуре |
факт |
Далее находится влияние структуры реализованной продукции на сумму выручки. Результаты расчетов требуется представить в табличной форме самостоятельно и сделать соответствующие выводы по каждому пункту проведенного анализа.
4.4.3 Анализ использования ресурсов предприятия.
Анализ использования ресурсов предприятия проводится по следующим пунктам:
анализ использования трудовых ресурсов;
анализ использования основных производственных фондов;
анализ использования материальных ресурсов
Исходные данные для анализа использования трудовых ресурсов необходимо свести в таблицу 7.
Таблица 7 - Исходные данные для анализа использования трудовых ресурсов
| Показатели |
План |
Факт |
| 1 Среднегодовая численность промышленно-производственного персонала |
| 2 Число отработанных рабочими человеко-дней |
3 Число человеко-часов, отработанных промышленно-производственным персоналом - всего
в т. ч. сверхурочно
|
Результаты расчетов представить в таблице 8 и сделать соответствующие выводы
Таблица 8 - Использование трудовых ресурсов предприятия
| Показатели |
План |
Факт |
Отклонение (+, - -) |
| 1 Среднегодовая численность промышленно-производственного персонала, чел. |
2 Отработано за год одним рабочим: дней
часов
|
| 3 Средняя продолжительность рабочего дня (с тремя десятичными знаками), ч. |
| 4 Фонд рабочего времени, тыс. часов |
| 5 В том числе сверхурочно отработанное время, тыс. часов |
Использование основных производственных фондов необходимо оценить с помощью анализа фондоотдачи. Результаты свести в таблицу 9.
Таблица 9 - Расчет фондоотдачи
| Показатели |
Единица измерения |
Отчетный год |
| План |
Факт |
+, - - |
| Объем выпуска продукции |
Тыс. тг. |
| Среднегодовая стоимость ОПФ |
Тыс. тг. |
| Фондоотдача |
Далее находится влияние факторов на фондоотдачу методом цепных подстановок.
Анализ использования материальных ресурсов необходимо произвести с помощью факторного анализа материалоемкости отдельного вида продукции (частной материалоемкости). Частная материалоемкость зависит от норм расхода материалов (УР), стоимости материалов (ЦМ) и отпускных цен на продукцию (ЦП). Исходные данные в таблице 10.
Таблица 10 - Исходные данные для расчета частной материалоемкости
Вид
изделия
|
Нормы расхода материалов, тг. на единицу (УР) |
Стоимость материалов, тг.
(ЦМ)
|
Оптовая цена на продукцию, тг.
(ЦП)
|
| План |
Факт |
План |
Факт |
План |
Факт |
| Изделие 1 |
| Изделие 2 |
| Изделие 3 |
| Изделие 4 |
Далее методом цепных подстановок производится факторный анализ частной материалоемкости, результаты свести в таблицу 11.
Таблица 11 - Факторный анализ частной материалоемкости
Вид
изделия
|
Материалоемкость, тг. |
Отклонение от плана, тг. |
| План |
Усл.1 |
Усл.2 |
Факт |
Общее |
В т. ч. за счет изменения |
| Нормы расх-а сырья |
Цен на сырье |
Оптовых цен на прод. |
| Изделие 1 |
| Изделие 2 |
| Изделие 3 |
| Изделие 4 |
По результатам расчетов сделать выводы.
4.4.4 Анализ прибыли и рентабельности.
Анализ прибыли и рентабельности предприятия необходимо провести с помощью факторного анализа. Исходные данные сводятся в следующую таблицу.
Таблица 12 - Исходные данные для анализа прибыли и рентабельности
| Показатели |
Отчетный год |
| план |
факт |
| 1 Объем реализованной продукции |
| 2 Цена единицы продукции |
| 3 Себестоимость единицы продукции |
Оценить выполнение плана прибыли, а также влияние каждого из факторов на изменение суммы прибыли от реализации продукции методом абсолютных разниц.
Затем следует сделать факторный анализ рентабельности методом цепных подстановок.
Курсовая работа завершается выводом по проведенному анализу, оценкой производственно-хозяйственной деятельности предприятия.
5. Методические указания к выполнению курсовой работы
5.1 Методические указания по выполнению задания 1
5.1.1 Корреляционно-регрессионный анализ. Метод корреляционно-регрессионного анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости. Для прямолинейной зависимости исчисляется коэффициент корреляции.
Регрессия - это статистический метод, позволяющий найти уравнение, которое наилучшим образом описывает множество данных. Многомерная регрессия выполняет анализ для нескольких множеств данных; это часто дает более реалистичный прогноз.
5.1.2 Организация компьютерной обработки экономической информации. MicrosoftExcel предлагает широкий диапазон средств для обработки экономической информации.
Excel предоставляет несколько функций с линейной регрессией - линейн, тенденция, предсказ, наклон - и две - логарифприбл и рост - для экспоненциальной регрессии. Эти функции вводятся в виде формулы массива и возвращают массив результатов. Каждую из этих функций можно использовать с одной или несколькими независимыми переменными.
Функция линейн.
Рассчитывает статистику для ряда с применением метода наименьших квадратов, чтобы вычислить прямую линию, которая наилучшим образом аппроксимирует имеющиеся данные. Функция возвращает массив, который описывает полученную прямую. Поскольку возвращается массив значений, функция должна задаваться в виде формулы массива. Для получения дополнительных сведений о формулах массива нажмите кнопку.
Уравнение для прямой линии имеет следующий вид:
y = mx + b или
y = m1x1 + m2x2 +... + b
(в случае нескольких интервалов значений x), где зависимое значение y является функцией независимого значения x. Значения m - это коэффициенты, соответствующие каждой независимой переменной x, а b - это постоянная. Функция линейн возвращает массив {mn; mn-1;...; m1; b}. Линейн может также возвращать дополнительную регрессионную статистику.
Известные значения y - это множество значений y, которые уже известны для соотношения y = mx + b.
Если массив известные значения y имеет один столбец, то каждый столбец массива известные значения x интерпретируется как отдельная переменная.
Если массив известные значения y имеет одну строку, то каждая строка массива известные значения x интерпретируется как отдельная переменная.
Известные значения x - это необязательное множество значений x, которые уже известны для соотношения y = mx + b.
Массив известные значения x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то известные значения y и известные значения x могут быть массивами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то известные значения y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец).
Если известные значения x опущены, то предполагается, что это массив {1; 2; 3;... } такого же размера как и известные значения y.
Конст - это логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
Если конст имеет значение истина или опущено, то b вычисляется обычным образом.
Если конст имеет значение ложь, то b полагается равным 0 и значения m подбираются так, чтобы выполнялось соотношение y = mx.
Статистика - это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии.
Если статистика имеет значение истина, то функция линейн возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид:
mn
mn-1
……………. m2
m1
b
sen
sen-1
. ……………. se2
se1
seb
r2
sey
F dF
Ssreg ssresid
Его описание представлено в таблице 13.
Если статистика имеет значение ложь или опущена, то функция линейн возвращает только коэффициенты m и постоянную b.
Точность аппроксимации с помощью прямой, вычисленной функцией линейн, зависит от степени разброса данных. Чем ближе данные к прямой, тем более точной является модель, используемая функцией линейн. Функция линейн использует метод наименьших квадратов для определения наилучшей аппроксимации данных.
Проводя регрессионный анализ, Microsoft Excel вычисляет для каждой точки квадрат разности между прогнозируемым значением y и фактическим значением y. Сумма этих квадратов разностей называется остаточной суммой квадратов. Затем Microsoft Excel подсчитывает сумму квадратов разностей между фактическими значениями y и средним значением y, которая называется общей суммой квадратов (регрессионная сумма квадратов + остаточная сумма квадратов). Чем меньше остаточная сумма квадратов по сравнению с общей суммой квадратов, тем больше значение коэффициента детерминированности r2, который показывает, насколько хорошо уравнение, полученное с помощью регрессионного анализа, объясняет взаимосвязи между переменными.
Таблица 13 - Описание элементов возвращаемого массива
| Величина |
Описание
|
| Se1
,se2
,...,sen
|
Стандартные значения ошибок для коэффициентов m1
, m2
,...,mn
. |
| seb
|
Стандартное значение ошибки для постоянной b (seb = #Н/Д, если конст имеет значение ЛОЖЬ). |
| r2
|
Коэффициент детерминации. Сравниваются фактические значения y и значения, получаемые из уравнения прямой; по результатам сравнения вычисляется коэффициент детерминации, нормированный от 0 до 1. Если он равен 1, то имеет место полная корреляция с моделью, т.е. нет различия между фактическим и оценочным значениями y. В противоположном случае, если коэффициент детерминации равен 0, то уравнение регрессии неудачно для предсказания значений y. |
| sey
|
Стандартная ошибка для оценки y. |
| F |
F-статистика, или F-наблюдаемое значение. F-статистика используется для определения того, является ли наблюдаемая взаимосвязь между зависимой и независимой переменными случайно или нет. |
| dF |
Степени свободы. Степени свободы полезны для нахождения F-критических значений в статистической таблице. Для определения уровня надежности модели нужно сравнить значения в таблице с F - статистикой, возвращаемой функцией ЛИНЕЙН. |
| ssreg |
Регрессионая сумма квадратов. |
| ssresid |
Остаточная сумма квадратов. |
5.2 Методические указания по выполнению задания 2
5.2.1 Способ цепной подстановки
Одним из важнейших методологических вопросов в АХД является определение величины влияния отдельных факторов на прирост результативных показателей. В детерминированном анализе для этого используются следующие способы: цепной подстановки, индексный, абсолютных разниц, относительных разниц, пропорционального деления и интегральный метод.
Первые четыре способа основываются на методе элиминирования. Элиминировать - это значит устранить, отклонить, исключить воздействие всех факторов на величину результативного показателя кроме одного. Этот метод исходит из того, что все факторы изменяются независимо друг от друга: сначала изменяется один, а все другие остаются без изменения, потом изменяются два, затем три и т.д., при неизменности остальных. Это позволяет определить влияние каждого фактора на величину исследуемого показателя в отдельности.
Наиболее универсальным из них является способ цепной подстановки. Он используется для расчета влияния факторов во всех типах детерминированных факторных моделей: аддитивных, мультипликативных, кратных и смешанных (комбинированных). Этот способ позволяет определить влияние отдельных факторов на изменение величины результативного показателя путем постепенной замены базисной величины каждого факторного показателя в объеме результативного показателя на фактическую в отчетном периоде.
С этой целью определяют ряд условных величин результативного показателя, которые учитывают изменение одного, затем двух, трех и т.д. факторов, допуская, что остальные не меняются. Сравнение величины результативного показателя до и после изменения уровня того или другого фактора позволяет элиминироваться от влияния всех факторов, кроме одного, и определить воздействие последнего на прирост результативного показателя.
Порядок применения этого способа рассмотрим на следующем примере (табл.14).
Как нам уже известно, объем валовой продукции (ВП) зависит от двух основных факторов первого уровня: численности рабочих (КР) и среднегодовой выработки {ГВ). Имеем двухфакторную мультипликативную модель:
ВП = КР * ГВ.
Алгоритм расчета способом цепной подстановки для этой модели:
ВПпл
= КРпл
*ГВпл
= 1000*160 = 160000 млн тенге.,
ВПусл
= КРф*ГВ усл
= 1200*160 = 192000 млн тенге,
ВПф
= КРф
*ГВф
= 1200*200 = 240000 млн тенге.
Как видим, второй показатель валовой продукции отличается от первого тем, что при его расчете принята фактическая численность рабочих вместо запланированной. Среднегодовая выработка продукции одним рабочим в том и другом случае плановая. Значит за счет увеличения количества рабочих выпуск продукции увеличился на 32 000 млн тг. (192 000 - 160 000).
Третий показатель отличается от второго тем, что при расчете его величины выработка рабочих принята по фактическому уровню вместо плановой. Количество же работников в обоих случаях фактическое. Отсюда за счет повышения производительности труда объем валовой продукции увеличился на 48 000 млн тг. (240 000 - 192 000).
Таким образом, перевыполнение плана по объему валовой продукции явилось результатом влияния следующих факторов:
а) увеличения численности рабочих + 32 000 млн тг.
б) повышения уровня производительности труда + 48 000 млн тг.
Итого + 80 000 млн тг.
Таблица 14 - Данные для факторного анализа объема валовой продукции
Показатель
|
Условное обознач.
|
План
|
Факт
|
+,-
|
Выполнение плана, % |
| Валовая продукция, тыс. тг. |
ВП |
160000 |
240 000 |
+80 000 |
150 |
Среднегодовая численность рабочих, чел.
|
КР
|
1000
|
1200
|
+200
|
120
|
Отработано всеми рабочими за год:
Дней
Часов
|
SD
t
|
250000 2000000
|
307 200
2 334 720
|
+57 200 +334 720
|
122,88 116,736
|
Среднегодовая выработка на одного рабочего, млн тг.
|
ГВ
|
160
|
200
|
+40
|
125
|
Количество отработанных дней одним рабочим за год
|
Д
|
250
|
256
|
+6
|
102,4
|
Среднедневная выработка продукции одним рабочим, тыс. тг
|
ДВ
|
640
|
781,25
|
+141,25
|
122,1
|
Средняя продолжительность рабочего дня,
|
П
|
8
|
7,6
|
-0,4
|
95
|
Среднечасовая выработка, тыс. тг.
|
СВ
|
80
|
102,796
|
+22,796
|
128,5
|
Алгебраическая сумма влияния факторов обязательно должна быть равна общему приросту результативного показателя:
DВПкр
+ DВПГВ
= DВПобщ
Отсутствие равенства свидетельствует о допущенных ошибках в расчетах.
Для наглядности результаты анализа приведены в табл.15
Таблица 15 - Результаты факторного анализа валовой продукции
Показатель
|
Численность рабочих
|
Годовая выработка, млн тг.
|
Валовая продукция, млрд тг.
|
Отклонение от плана
|
План
|
факт
|
план
|
факт
|
план
|
Усл.
|
факт
|
всего
|
в т. ч. за счет
|
КР
|
ГВ
|
Цех 1
|
200
|
220
|
180
|
210
|
36
|
39,6
|
46,2
|
+10,2
|
+3,6
|
+6,6
|
Цех 2
|
370
|
400
|
150
|
165
|
55,5
|
60,0
|
66,0
|
+10,5
|
+4,5
|
+6,0
|
И т.д.
|
Всего
|
1000
|
1200
|
160
|
200
|
160
|
192
|
240
|
+80
|
+32
|
+48
|
Если требуется определить влияние трех факторов, то в этом случае рассчитывается не один, а два условных дополнительных показателя, т.е. количество условных показателей на единицу меньше количества факторов. Проиллюстрируем это на четырехфакторной модели валовой продукции:
ВП = КР * Д * П * СВ.
Исходные данные для решения задачи приведены в табл.15:
ВПпл
= КРпл
* Дпл
* Ппл
* СВпл
= 1000 * 250 * 8 *80 = 160000 млн тг.;
ВПусл1
= КРф
* Дпл
* Ппл
* СВпл
= 1200 * 250 * 8 * 80 = 192000 млн тг.;
ВПусл2
= КРф
* Дф
* Ппл
* СВпл
= 1200 * 256 * 8* 80 =196608 млн тг.;
ВПусл3
= КРф
* Дф
* Пф
* СВпл
= 1200 * 256 * 7,6 * 80 = 186778 млн тг.;
ВПф
= КРф
* Дф
* Пф * СВф = 1200 * 256 * 7,6 * 102,796 = 240000 млн тг.;
План по выпуску продукции в целом перевыполнен на 80000 млн тг. (240000 - 160000), в том числе за счет изменения:
а) количества рабочих
DВПкр
= ВПусл1
- ВПпл
= 192000 - 160000 = +32000;
б) количества отработанных дней одним рабочим за год
DВПд
= ВПусл2
- ВПусл1
= 196608 - 192000 = +4608;
в) средней продолжительности рабочего дня
DВПп
= ВПусл3
- ВПусл2
= 186778 - 196608 = - 9830;
г) среднечасовой выработки
DВПсв
= ВПф
- ВПусл3
= 240000-186778 =+53222.
Всего + 80 000 млн тг.
Используя способ цепной подстановки, следует придерживаться следующей последовательности расчетов: в первую очередь нужно учитывать изменение количественных, а затем качественных показателей. Если же имеется несколько количественных и несколько качественных показателей, то сначала следует изменить величину факторов первого уровня подчинения, а потом более низкого. В приведенном примере объем производства продукции зависит от четырех факторов: количества рабочих, количества отработанных дней одним рабочим, продолжительности рабочего дня и среднечасовой выработки.
Таким образом, применение способа цепной подстановки требует знания взаимосвязи факторов, их соподчиненности, умения правильно их классифицировать и систематизировать.
Мы рассмотрели пример расчета влияния факторов на прирост результативного показателя в мультипликативных моделях.
В кратных моделях алгоритм расчета факторов на величину исследуемых показателей следующий:

где ФО - фондоотдача; ВП - валовая продукция; ОПФ - среднегодовая стоимость основных производственных фондов.
Методика расчета влияния факторов в смешанных моделях:

где П - сумма прибыли от реализации продукции; VPП - объем реализации продукции;
Ц - цена реализации; С - себестоимость единицы продукции;
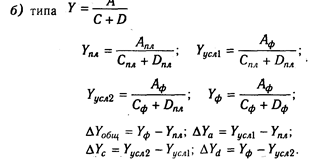
Аналогичным образом рассчитывают влияние факторов и по другим детерминированным моделям смешанного типа.
Отдельно необходимо остановиться на методике определения влияния структурного фактора на прирост результативного показателя с помощью этого способа. Например, выручка от реализации продукции (В) зависит не только от цены (Ц) и количества проданной продукции (VРП), но и от ее структуры (УДi
) Если возрастет доля продукции высшей категории качества, которая продается по более высоким ценам, то выручка за счет этого увеличится, и наоборот. Факторная модель этого показателя может быть записана так:

В процессе анализа необходимо элиминироваться от воздействия всех факторов, кроме структуры продукции. Для этого сравниваем следующие показатели выручки:

Разность. между этими показателями учитывает изменение выручки от реализации продукции за счет изменения ее структуры (табл.).
Из таблицы видно, что в связи с увеличением удельного веса молока второго сорта в общем объеме его реализации выручка уменьшилась на 10 млн тенге. (655 - 665). Это неиспользованный резерв хозяйства.
Таблица 16 - Расчет влияния структурного фактора на изменение выручки от реализации продукции способом цепной подстановки
Сорт
молока
|
Цена 1 т,
тыс. тг.
|
Объем реа-
лизации, т
|
Структура
Продукции
|
Фактический VPП при плановой структуре, т |
Выручка, млн тенге. за VРПф при УДi, |
План
|
Факт
|
план
|
факт
|
план
|
факт
|
1
|
2700
|
180
|
200
|
0,9
|
0,8
|
225
|
607,5
|
540
|
2
|
2300
|
20
|
50
|
0,1
|
0,2
|
25
|
57,5
|
115
|
Итого
|
-
|
200
|
250
|
1,0
|
1,0
|
250
|
665,0
|
655
|
5.2.2 Индексный метод
Индексный метод основан на относительных показателях динамики, пространственных сравнений, выполнения плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому или по другому объекту).
С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.
К примеру возьмем индекс стоимости товарной продукции:

Он отражает изменение физического объема товарной продукции (q) и цен (р) и равен произведению этих индексов:
Iтп =
Iq *
Ip
Чтобы установить, как изменилась стоимость товарной продукции за счет количества произведенной продукции и за счет цен, нужно рассчитать индекс физического объема Iq и индекс цен Iр:
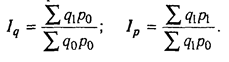
В нашем примере объем валовой продукции можно представить в виде произведения численности рабочих и их среднегодовой выработки.
Следовательно, индекс валовой продукции Iвп будет равен произведению индекса численности рабочих (количество) Iкр и индекса среднегодовой выработки Iгв:

Iвп = Iкр * Iгв = 1,2 * 1,25 = 1,5
Если из числителя вышеприведенных формул вычесть знаменатель, то получим абсолютные приросты валовой продукции в целом и за счет каждого фактора в отдельности, т.е. те же результаты, что и способом цепных подстановок.
5.2.3 Способ абсолютных разниц
Способ абсолютных разниц является одной из модификаций элиминирования. Как и способ цепной подстановки, он применяется для расчета влияния факторов на прирост результативного показателя в детерминированном анализе, но только в мультипликативных и смешанных моделях типа: Y = (а - Ь) с и Y = a (b - с). И хотя его использование ограничено, но благодаря своей простоте он получил широкое применение в АХД. Особенно эффективно применяется этот способ в том случае, если исходные данные уже содержат абсолютные отклонения по факторным показателям.
При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого фактора на базовую (плановую) величину факторов, которые находятся справа от него, и на фактическую величину факторов, расположенных слева от него в модели.
Рассмотрим алгоритм расчета для мультипликативной факторной модели типа Y=a*b*c*d. Имеются плановые и фактические значения по каждому факторному показателю, а также их абсолютные отклонения:
∆а = Аф - Апл; ∆
b = Вф - Впл;
∆с = Сф - Спл; ∆
d = Dф -
Dпл.
Определяем изменение величины результативного показателя за счет каждого фактора:
∆
Ya = ∆а * Впл * Спл *
Dпл;
∆
Yb = Аф * ∆
b * Спл *
Dпл;
∆
Yc = Аф * Вф * ∆с *
Dпл;
∆
Ya = Аф * Вф * Сф * ∆
D
Как видно из приведенной схемы, подсчет строится на последовательной замене плановых значений факторных показателей на их отклонения, а затем на фактический уровень этих показателей.
Возьмем числовой пример. Рассмотрим методику расчета влияния факторов этим способом относительно четырехфакторной мультипликативной модели валовой продукции:
ВП = КР * Д * П * ЧВ
∆ ВПкр = (КРф - КРпл) Дпл * Ппл * ЧВпл= (1200 - 1000) *250*8,0*80,0 = +32000;
∆ ВПд = КРф (Дф - Дпл) Ппл * ЧВпл =1200 * (256 - 250) * 8,0 * 80,0 = +4608;
∆ ВПп= КРф * Дф (Пф - Ппл) ЧВпл =1200 * 256 * (7,6 - 8,0) * 80,0 = - 9830;
∆ВПсв = КРф * Дф * Пф (ЧВф - ЧВпл) =1200*256 * 7,6 * (102,796 - 80) = +53222
Всего + 80 000
Таким образом, способ абсолютных разниц дает те же результаты, что и способ цепной подстановки.
Здесь также необходимо следить за тем, чтобы алгебраическая сумма прироста результативного показателя за счет отдельных факторов была равна общему его приросту.
Рассмотрим алгоритм расчета факторов этим способом в смешанных моделях типа Y = (a - Ь) с. Для примера возьмем факторную модель прибыли от реализации продукции.
П = VРП (Ц - С)
Прирост суммы прибыли за счет изменения объема реализации продукции:
∆П
vpn = ∆
VРП (Цпл - Спл);
цены реализации:
∆Пц, =
VРПф * ∆Ц;
себестоимости продукции:
∆ Пс= VРПф (-∆С)
Расчет влияния структурного фактора при помощи этого способа проводится следующим образом:
∆П = ∑ [ (УДфi - УДплi) * Цi] * VРПобщ. ф.
Как видно из таблицы 17, за счет изменения структуры реализации средняя цена за 1 т молока уменьшилась на 40 тыс. тг., а за весь фактический объем реализации продукции прибыли было получено меньше на сумму 10 млн тенге. (40 тыс. тг. * 250 т).
Таблица 17 - Расчет влияния структурного фактора способом абсолютных разниц
Сорт молока
|
Цена 1т, тыс. руб.
|
Структура продукции,
|
Изменение средней цены реализации за счет структуры продукции, тыс. тг.
|
план
|
факт
|
+,-
|
1
|
2700
|
0,9
|
0,8
|
-0,1
|
-270
|
2
|
2300
|
0,1
|
0,2
|
+0,1
|
+230
|
Всего
|
-
|
1,0
|
1,0
|
-
|
-40
|
5.2.4 Способ относительных разниц
Способ относительных разниц, как и предыдущий, применяется для измерения влияния факторов на прирост результативного показателя только в мультипликативных моделях и комбинированных типа Y = (а - Ь) с. Он значительно проще цепных подстановок, что при определенных обстоятельствах делает его очень эффективным. Это прежде всего касается тех случаев, когда исходные данные содержат уже определенные ранее относительные отклонения факторных показателей в процентах или коэффициентах.
Рассмотрим методику расчета влияния факторов этим способом для мультипликативных моделей типа Y = А * В * С. Сначала необходимо рассчитать относительные отклонения факторных показателей:

Тогда отклонение результативного показателя за счет каждого фактора определяется следующим образом:
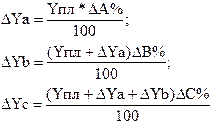
Согласно этому правилу, для расчета влияния первого фактора необходимо базисную (плановую) величину результативного показателя умножить на относительный прирост первого фактора, выраженного в процентах, и результат разделить на 100.
Чтобы рассчитать влияние второго фактора, нужно к плановой величине результативного показателя прибавить изменение его за счет первого фактора и затем полученную сумму умножить на относительный прирост второго фактора в процентах и результат разделить на 100.
Влияние третьего фактора определяется аналогично: к плановой величине результативного показателя необходимо прибавить его прирост за счет первого и второго факторов и полученную сумму умножить на относительный прирост третьего фактора и т.д.
Закрепим рассмотренную методику на примере, приведенном в табл.15:
 
Как видим, результаты расчетов те же, что и при использовании предыдущих способов.
Способ относительных разниц удобно применять в тех случаях, когда требуется рассчитать влияние большого комплекса факторов (8-10 и более). В отличие от предыдущих способов значительно сокращается количество вычислений.
5.2.5 Способ пропорционального деления и долевого участия.
В ряде случаев для определения величины влияния факторов на прирост результативного показателя может быть использован способ пропорционального деления. Это касается тех случаев, когда мы имеем дело с аддитивными моделями типа Y = ∑Хi
и смешанными типа

В первом случае, когда имеем одноуровневую модель типа У = а + b + с, расчет проводится следующим образом:

Например, уровень рентабельности снизился на 8% в связи с увеличением капитала предприятия на 200 млн тг. При этом стоимость основного капитала возросла на 250 млн тг., а оборотного уменьшилась на 50 млн тг. Значит, за счет первого фактора уровень рентабельности снизился, а за счет второго - повысился:

Методика расчета для смешанных моделей несколько сложнее.
Когда известны ∆Вd; ∆Вn и ∆Вm а также ∆Yb то для определения ∆Yd, ∆Yn, ∆Ym можно использовать способ пропорционального деления, который основан на пропорциональном распределении прироста результативного показателя Y за счет изменения фактора В между факторами второго уровня D, N и М соответственно их величине. Пропорциональность этого распределения достигается путем определения постоянного для всех факторов коэффициента, который показывает величину изменения результативного показателя Y за счет изменения фактора В на единицу.
Величина коэффициента (К) определяется следующим образом:

Умножив этот коэффициент на абсолютное отклонение В за счет соответствующего фактора, найдем отклонения результативного показателя:
∆
Yb=К*∆
Bd; ∆
Yn=К*∆
Bn; ∆
Ym=К*∆
Bm
Например, себестоимость 1 т/км за счет снижения среднегодовой выработки автомобиля повысилась на 180 руб. При этом известно, что среднегодовая выработка автомашины снизилась из-за:
а) сверхплановых простоев машин - 5000 т/км
б) сверхплановых холостых пробегов - 4000 т/км
в) неполного использования грузоподъемности - 3000 т/км
Всего-12000 т/км
Отсюда можно определить изменение себестоимости под влиянием факторов второго уровня:

Таблица 18 - Расчет влияния факторов на результативный показатель способом долевого участия
Показатель
|
Изменение годовой выработки машины, т/км
|
Доля показателей в общем изменении годовой выработки,%
|
Изменение себестоимости 1 т/км, руб.
|
Сверхплановые простои машин
|
-5000
|
41,67
|
+75
|
Сверхплановые холостые пробеги
|
-4000
|
33,33
|
+60
|
Неполное использование
грузоподъемности машин
|
-3000
|
25,00
|
+45
|
Всего
|
-12000
|
100,00
|
+180
|
Для решения такого типа задач можно использовать также способ долевого участия. Для этого сначала определяется доля каждого фактора в общей сумме их приростов, которая затем умножается на общий прирост результативного показателя:

Аналогичных примеров применения этого способа в АХД можно привести очень много, в чем вы сможете убедиться в процессе изучения отраслевого курса анализа хозяйственной деятельности на предприятиях.
5.2.6 Способ логарифмирования в анализе хозяйственной деятельности.
Способ логарифмирования применяется для измерения влияния факторов в мультипликативных моделях. В данном случае peзyльтат расчета, как и при интегрировании, не зависит от месторасположения факторов в модели и по сравнению с интегральным методом обеспечивается более высокая точность расчетов. Если п интегрировании дополнительный прирост от взаимодействия факторов распределяется поровну между ними, то с помощью логарифмирования результат совместного действия факторов pacпpeдeляется пропорционально доли изолированного влияния каждого фактора на уровень результативного показателя. В этом его преимущество, а недостаток - в ограниченности сферы его применения.
В отличие от интегрального метода при логарифмировании пользуются не абсолютные приросты показателей, а индексы роста (снижения).
Математически этот метод описывается следующим образе Допустим, что результативный показатель можно представить виде произведения трех факторов: F = xyz. Прологарифмировав обе части равенства, получим

Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, произведем замену абсолютных их значений на индексы:
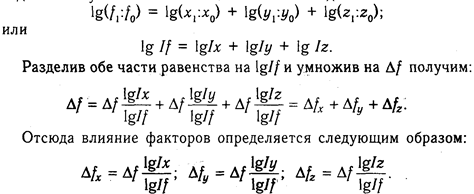
Из формул вытекает, что общий прирост результативного показателя распределяется по факторам пропорционально отношениям логарифмов факторных индексов к логарифму результативного показателя. И не имеет значения, какой логарифм используется - натуральный или десятичный.
Сравнив полученные результаты расчета влияния факторов разными способами по данной факторной модели, можно убедиться в преимуществе способа логарифмирования. Это выражается в относительной простоте вычислений и повышении точности расчетов.
Рассмотрев основные приемы детерминированного факторного анализа и сферу их применения, результаты можно систематизировать в виде следующей матрицы:
Таблица 19 - Детерминированные факторные приемы и модели
 Модели Модели
Приемы
|
Мультипликативные
|
Аддитивные
|
Кратные
|
Смешанные
|
Цепной подстановки
|
+
|
+
|
+
|
+
|
Индексный
|
+
|
-
|
+
|
-
|
Абсолютных разниц
|
+
|
-
|
-
|
Y=a (b-c}
|
Относительных разниц
|
+
|
-
|
-
|
-
|
Пропорционального деления (долевого участия)
|
-
|
+
|
-
|
Y=а/Sxi
|
Интегральный
|
+
|
-
|
+
|
Y= а/Sxi
|
Логарифмирования
|
+
|
-
|
-
|
-
|
Список литературы
1. Баканов М.И., Шеремет А.Д., Теория экономического анализа. - М.: Финансы и статистика, 2000.
2. Савицкая Г.В. Анализ хозяйственной деятельности предприятия: Учебное пособие. - Мн.: ИП "Экоперспектива", 2000. - 498 с.
3. Методика экономического анализа промышленного предприятия (объединения) / Под ред. А.И. Бужинского, А.Д. Шеремета. - М.: Финансы и статистика, 1988
4. Муравьева А.И. Теория экономического анализа. - М.: Финансы и статистика, 1988.
|