МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Институт математики и компьютерных наук
Кафедра математики и информатики
Курсовая работа
«Изучение и анализ различных способов определение тригонометрических функций»
Выполнил:
студентка 362 группы
Латфуллина Р.А.
Научный руководитель:
к.ф.-м.н., доцент
Шармина Т.Н.
Тюмень - 2010
Содержание
Введение. 3
Глава1. Функции 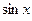 , , 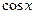 как решения некоторых задач Коши. 5 как решения некоторых задач Коши. 5
Глава2. Аналитическая теория тригонометрических функций. 16
Список литературы.. 22
Данная курсовая работа посвящена изучению и анализу различных способов определения тригонометрических функций.
Тригонометрические функции являются важной составной частью содержания математического образования, как в средних, так и в высших учебных заведениях и часто встречаются в различных приложениях математики. С их помощью могут быть построены и изучены математические модели процессов реального мира. Для школьных учителей полезно знать различные подходы к определению и изучению свойств тригонометрических функций. Имеется не так много математической литературы в которой теория элементарных функций излагается последовательно и подробно разными методами. В этом и заключается актуальность данной темы.
Объектом нашего исследования мы выбрали тригонометрические функции. Предметом же является способы их определения.
Целью курсовой работы является изучение и анализ различных способов определения тригонометрических функций.
Для достижения цели мы поставили следующие задачи: изучить математическую литературу, проанализировать способы определения тригонометрических функций и доказать свойства этих функций на основе соответствующего способа определения.
Курсовая работа состоит из введения, двух глав и списка литературы.
В главе 1 излагается способ построения теории функций 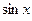 , , 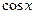 , основываясь на использовании теоремы существования и единственности решения соответствующей задачи Коши и простейших сведений из дифференциального и интегрального исчисления. Также в этой главе приведены доказательства основных свойств этих функций. , основываясь на использовании теоремы существования и единственности решения соответствующей задачи Коши и простейших сведений из дифференциального и интегрального исчисления. Также в этой главе приведены доказательства основных свойств этих функций.
Глава 2 посвящена рассмотрению теории тригонометрических функций на базе степенных рядов и установлению эквивалентности нового и традиционного определения таких функций.
Также в работе проведены доказательства некоторых свойств тригонометрических функций.
Глава1. Функции 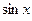 , , 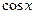 как решения некоторых задач Коши как решения некоторых задач Коши
Для линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами теорема существования и единственности решения задачи Коши формулируется следующим образом.
Теорема1
.
Дифференциальное уравнение
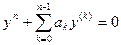 , ,
где 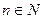 ; ; 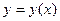 ; ; 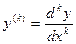 ; ; 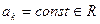 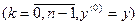 , имеет на , имеет на 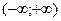 единственное n-кратно дифференцируемое решение единственное n-кратно дифференцируемое решение 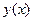 , удовлетворяющее условиям , удовлетворяющее условиям
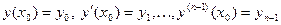
(здесь 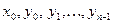 - произвольно заданные фиксированные действительные числа). - произвольно заданные фиксированные действительные числа).
Очевидно, что это решение обладает на 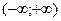 непрерывными производными всех порядков. непрерывными производными всех порядков.
В частности, когда 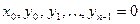 , указанное в теореме 1 решение тривиально ( , указанное в теореме 1 решение тривиально (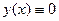 на на 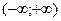 ). ).
Рассмотрим следующие две задачи Коши:
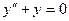 , , 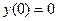 , , 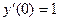 ; (1) ; (1)
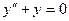 , , 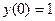 , , 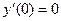 , (2) , (2)
где 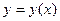 ; ; 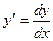 ; ; 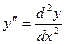 . Их решения обозначим соответственно через . Их решения обозначим соответственно через  и и  . Согласно теореме 1, эти решения определены, непрерывны и бесконечно дифференцируемы на всей числовой прямой, причём . Согласно теореме 1, эти решения определены, непрерывны и бесконечно дифференцируемы на всей числовой прямой, причём 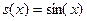 , , 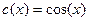 . Однако основные свойства функций . Однако основные свойства функций  , ,  установим, исходя из определения их как решения задач (1) и(2). установим, исходя из определения их как решения задач (1) и(2).
1.
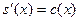 , , 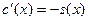 ( (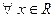 ). ).
Действительно, так как  и и  - решения уравнения - решения уравнения 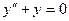 , то , то 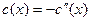 , , 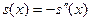 , откуда , откуда 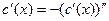 , , 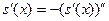 . Это значит, что каждая из функций . Это значит, что каждая из функций 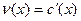 , , 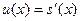 также являются решением уравнения также являются решением уравнения 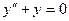 . При этом решения . При этом решения 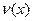 и и 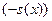 удовлетворяют одним и тем же начальным условиям: удовлетворяют одним и тем же начальным условиям: 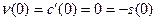 , , 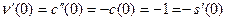 . Следовательно, по теореме существования и единственности . Следовательно, по теореме существования и единственности 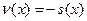 на на 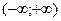 , т.е. , т.е. 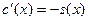 для для 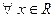 . .
Аналогично убеждаемся и в справедливости соотношения
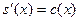 ( (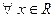 ). ).
2.
Функция  нечётная, а нечётная, а  чётная. чётная.
Доказательство: Прежде всего, области определения этих функций (совпадающие с 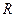 ) симметричны относительно точки ) симметричны относительно точки 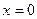 . Покажем теперь, что . Покажем теперь, что 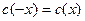 и и 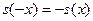 при любом при любом 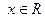 . .
Вводя в рассмотрение функции 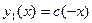 и и 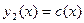 (тогда (тогда 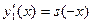 , , 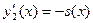 ) и учитывая свойство 1, будем иметь: ) и учитывая свойство 1, будем иметь:
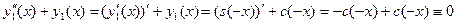 , ,
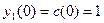 , , 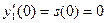 ; ;
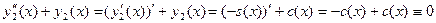 , ,
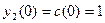 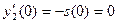 . .
Таким образом, функции 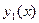 и и 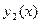 являются решением одной и той же задачи Коши являются решением одной и той же задачи Коши 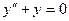 , , 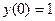 , , 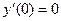 . Поэтому (согласно теореме 1) . Поэтому (согласно теореме 1) 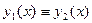 на на 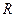 , т.е. , т.е. 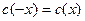 для любого для любого 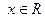 . .
Подобным же образом убеждаемся, что функция 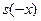 является решением задачи Коши является решением задачи Коши 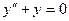 , , 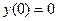 , , 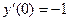 , следовательно, , следовательно, 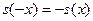 на на 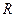 . .
3.
Имеет место тождество 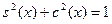 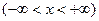 . .
Доказательство. Полагая 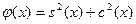 и используя свойство 1, находим и используя свойство 1, находим
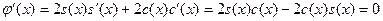 ( (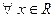 ), ),
Вследствие чего 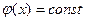 на на 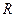 . А так как . А так как 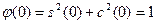 , то , то 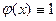 на на 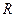 , т.е. , т.е. 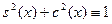 на на 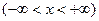 . .
Замечание.
Из свойства 3 следует, что функции  и и  ограничены
, причём ограничены
, причём 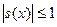 , , 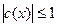 для любого для любого 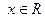 . .
4.
Справедливы следующие соотношения (теоремы сложения для функций
 и и  ):
):
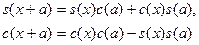 ( (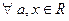 ) (3) Доказательство. Введём в рассмотрение функции ) (3) Доказательство. Введём в рассмотрение функции
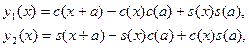
Считая (без ограничения общности) 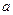 постоянной, а постоянной, а 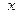 переменной. Эти функции являются решениями уравнения переменной. Эти функции являются решениями уравнения 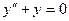 , удовлетворяющими нулевым условиям. Действительно, так как , удовлетворяющими нулевым условиям. Действительно, так как 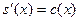 , , 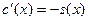 : :
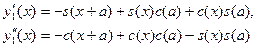
так что
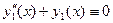 (на (на 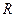 ), ),
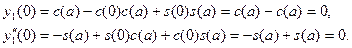
Аналогично
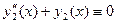 (на (на 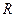 ), ), 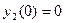 , , 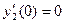 . .
Следовательно, согласно теореме 1, 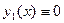 и и 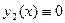 на на 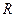 . Из этих тождеств непосредственно следуют требуемые соотношения. . Из этих тождеств непосредственно следуют требуемые соотношения.
Замечание.
Пологая в формулах (3) 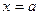 , получаем следующие формулы удвоения
: , получаем следующие формулы удвоения
:
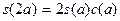 , , 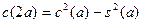 ( (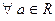 ). ).
Отсюда с учётом свойства 3 получаем:
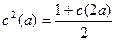 , , 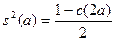 ( (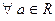 ). ).
Изучим теперь вопрос о нулях функций  , ,  , т.е. о корнях уравнений , т.е. о корнях уравнений 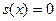 , , 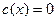 . Для краткости в дальнейшем нуль функции, принадлежащий . Для краткости в дальнейшем нуль функции, принадлежащий 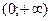 , будем называть её положительным нулём
. , будем называть её положительным нулём
.
Так как 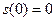 , то число , то число 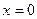 является одним из нулей функции является одним из нулей функции  . .
Лемма1
. Хотя бы одна из функций
 , ,  обладает по крайней мере одним положительным нулём. обладает по крайней мере одним положительным нулём.
Доказательство
.
Предположим (от противного), что уравнения 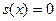 , , 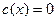 положительных решений не имеют. Тогда на положительных решений не имеют. Тогда на 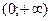 функции функции  и и  знакопостоянны. Действительно, если бы функция знакопостоянны. Действительно, если бы функция  или или  в некоторых точках в некоторых точках 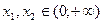 принимала значения противоположных знаков, то по теореме Больцано-Коши нашлась бы точка, заключённая между принимала значения противоположных знаков, то по теореме Больцано-Коши нашлась бы точка, заключённая между 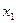 и и 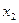 , в которой эта функция обращалась бы в нуль вопреки допущению. , в которой эта функция обращалась бы в нуль вопреки допущению.
Учитывая, далее, что 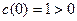 , заключаем, вследствие непрерывности , заключаем, вследствие непрерывности  , что , что  положительна в некоторой окрестности точки положительна в некоторой окрестности точки 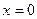 , и, следовательно, , и, следовательно, 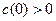 на на 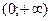 . .
Функция  возрастает на возрастает на 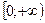 , так как , так как 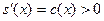 на на 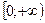 , а поскольку , а поскольку 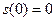 , то , то 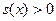 на на 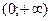 . С учётом свойства 3 и положительности функций . С учётом свойства 3 и положительности функций  , ,  на на 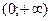 имеем имеем
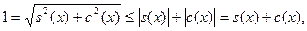
т.е. 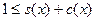 для любого для любого 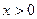 . Очевидно, сто последнее неравенство верно и при . Очевидно, сто последнее неравенство верно и при 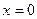 . Интегрируя почленно это неравенство по промежутку . Интегрируя почленно это неравенство по промежутку 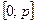 , где , где 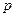 - любое положительное число, большее двух, получаем - любое положительное число, большее двух, получаем
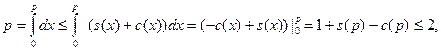
т.е. 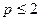 вопреки выбору числа вопреки выбору числа 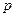 . Полученное противоречие и доказывает лемму. . Полученное противоречие и доказывает лемму.
Лемма2
.
Функция  имеет хотя бы один положительный нуль. имеет хотя бы один положительный нуль.
Доказательство.
Допустив противоречие, получим, что согласно лемме1, функция  обладает хотя бы одним положительным нулём обладает хотя бы одним положительным нулём 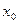 , а тогда (по формуле удвоения для функции , а тогда (по формуле удвоения для функции  ) будем иметь ) будем иметь
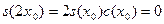 , ,
т.е. 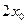 - положительный нуль функции - положительный нуль функции  , но это противоречит допущению. , но это противоречит допущению.
Замечание
.
Если 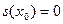 , то и , то и 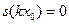 для любого для любого 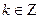 . .
Доказательство. Для 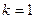 , , 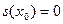 -это известно. -это известно.
Пусть для 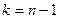 утверждение верно, т.е. утверждение верно, т.е. 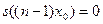 . Докажем справедливость утверждения для . Докажем справедливость утверждения для 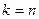 . .
Используя свойство 4, вычислим 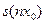 : :
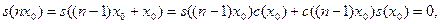
т.к. 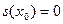 и и 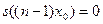 . .
5.
Существует наименьший положительный нуль
функции  . .
Доказательство. Обозначим через 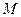 множество положительных нулей функции множество положительных нулей функции  . Это множество бесконечно (на основании леммы 2 и замечания к ней) и ограничено снизу (например, числом 0). Пусть . Это множество бесконечно (на основании леммы 2 и замечания к ней) и ограничено снизу (например, числом 0). Пусть 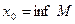 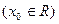 . Очевидно, что . Очевидно, что 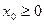 . Предположим теперь, что функция . Предположим теперь, что функция  не обладает наименьшим положительным нулём. С учётом этого предположения и определения точной нижней грани множества не обладает наименьшим положительным нулём. С учётом этого предположения и определения точной нижней грани множества 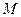 получаем, что получаем, что 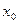 - предельная точка множества - предельная точка множества 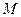 . Теперь легко убедиться, что . Теперь легко убедиться, что 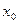 является одним из нулей функции является одним из нулей функции  . Действительно, . Действительно,
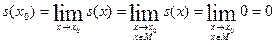
(здесь мы воспользовались непрерывностью функции  и теоремой о пределе функции (в нашем случае и теоремой о пределе функции (в нашем случае  ) в точке ) в точке 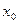 по данному множеству по данному множеству 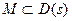 , для которого , для которого 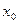 является предельной точкой). Отсюда следует, что является предельной точкой). Отсюда следует, что 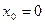 (поскольку в случае (поскольку в случае 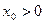 число число 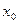 было бы наименьшим положительным нулём функции было бы наименьшим положительным нулём функции  вопреки сделанному выше предположению). вопреки сделанному выше предположению).
Но при 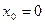 имеем имеем
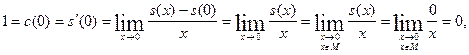
т.е. 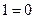 . Поскольку полученное равенство ложно, то наше допущение об отсутствии наименьшего положительного нуля функции . Поскольку полученное равенство ложно, то наше допущение об отсутствии наименьшего положительного нуля функции  неверно, и тем самым требуемое свойство доказано. неверно, и тем самым требуемое свойство доказано.
Обозначим наименьший положительный нуль функции  через через 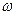 . Выясним свойства функций . Выясним свойства функций  и и  , прямо или косвенно связанные с числом , прямо или косвенно связанные с числом 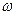 ( (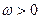 ). ).
6.
Функция  положительна на интервале положительна на интервале 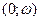 и отрицательна на интервале и отрицательна на интервале 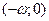 . .
7.
Функция  убывает на убывает на 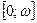 и возрастает на и возрастает на 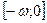 . .
8.
Числа вида 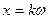 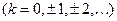 и только эти числа являются нулями функции и только эти числа являются нулями функции  . .
Доказательство. Согласно замечанию к лемме 2, 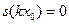 ( (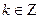 ). Если же ). Если же 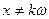 ( (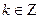 ), то ), то 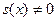 . Для доказательства этого допустим противное, т.е. предположим, что существует число . Для доказательства этого допустим противное, т.е. предположим, что существует число 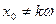 ( (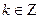 ), такое что ), такое что 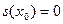 . Без ограничения общности (учитывая нечётность функции . Без ограничения общности (учитывая нечётность функции  ) можем считать, что ) можем считать, что 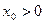 . Пусть . Пусть 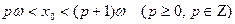 . Положим . Положим 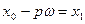 . Очевидно, что . Очевидно, что 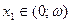 . Кроме того, на основании свойств 2 и 4 получим . Кроме того, на основании свойств 2 и 4 получим
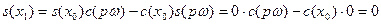
т.е. функция  имеет нуль в интервале имеет нуль в интервале  вопреки определению числа вопреки определению числа 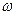 . .
9.
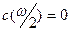 , , 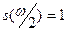 ; ; 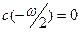 , , 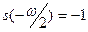 . .
10.
Функция  положительна на положительна на 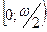 и отрицательна на и отрицательна на 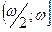 . .
Доказательство.
1) Докажем, что 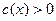 на на 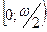 . .
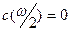 , , 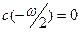 (по свойству 9). Найдём (по свойству 9). Найдём 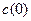 : :
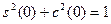 , т.к. , т.к. 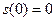 , то , то 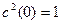 , следовательно , следовательно 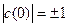 , т.е , т.е 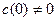 . Учитывая свойство 7 получим, что . Учитывая свойство 7 получим, что 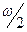 - наименьший положительный нуль функции - наименьший положительный нуль функции  . .
Учитывая, что 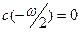 и свойство 7, получаем, что и свойство 7, получаем, что 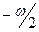 - наибольший отрицательный нуль функции - наибольший отрицательный нуль функции  . .
Таким образом, но интервале 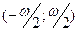 функция функция  не имеет нулей. По теореме Больцано-Коши функция не имеет нулей. По теореме Больцано-Коши функция  будет знакопостоянной на этом интервале. Кроме того, функция будет знакопостоянной на этом интервале. Кроме того, функция  положительна в некоторой правосторонней окрестности точки положительна в некоторой правосторонней окрестности точки 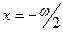 (в силу того, что (в силу того, что 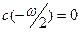 (по свойству 9) (по свойству 9) 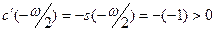 ). Следовательно, ). Следовательно, 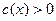 на всём интервале на всём интервале 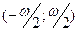 , следовательно, и на , следовательно, и на 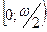 . .
2) Докажем, что 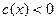 на на 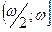 . .
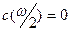 (по свойству 9). Найдём (по свойству 9). Найдём 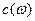 : :
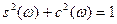 , т.к. , т.к. 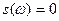 , то , то 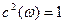 , следовательно , следовательно 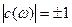 , т.е , т.е 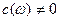 . Учитывая свойство 7 получим, что . Учитывая свойство 7 получим, что 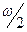 - наибольший отрицательный нуль функции - наибольший отрицательный нуль функции  . .
Таким образом, но интервале 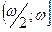 функция функция  не имеет нулей. По теореме Больцано-Коши функция не имеет нулей. По теореме Больцано-Коши функция  будет знакопостоянной на этом интервале. Кроме того, функция будет знакопостоянной на этом интервале. Кроме того, функция  отрицательна в некоторой правосторонней окрестности точки отрицательна в некоторой правосторонней окрестности точки 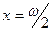 (в силу того, что (в силу того, что 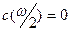 , , 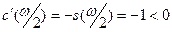 ). Следовательно, ). Следовательно, 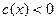 на всём интервале на всём интервале 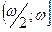 . .
11.
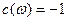 . .
Действительно, из равенства 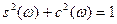 имеем имеем 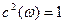 , откуда, учитывая, что , откуда, учитывая, что 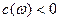 , получим , получим 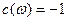 . .
12.
Функция  возрастает на возрастает на 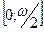 и убывает на и убывает на 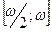 . .
Доказательство. Прежде всего, функция  непрерывна на каждом из отрезков непрерывна на каждом из отрезков 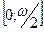 и и 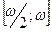 и дифференцируема на и дифференцируема на 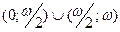 . .
Так как 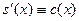 , то учитывая свойство 10, , то учитывая свойство 10, 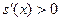 на на 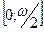 и и 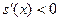 на на 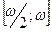 .Требуемое утверждение теперь непосредственно следует из теоремы о достаточных условиях убывания (возрастания) функции на промежутке. .Требуемое утверждение теперь непосредственно следует из теоремы о достаточных условиях убывания (возрастания) функции на промежутке.
Замечание
. Из свойства 2 и 12 следует, что функция убывает на 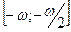 и возрастает на и возрастает на 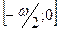 . .
13.
Функции  , , - периодические с периодом - периодические с периодом 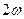 . .
Доказательство. Применяя теоремы сложения и учитывая, что 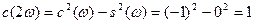 , , 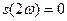 , имеем при любом , имеем при любом 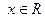 : :
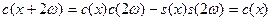 , ,
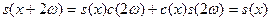 , ,
т.е. 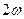 - период функций - период функций  , , . .
Докажем теперь, что ни одна из функций  , , не имеет положительного периода, меньше не имеет положительного периода, меньше 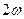 . Действительно, наличие такого периода у функции . Действительно, наличие такого периода у функции  противоречит свойству 7, а если бы таким периодом противоречит свойству 7, а если бы таким периодом 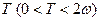 обладала функция обладала функция  , то мы имели бы , то мы имели бы 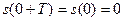 , т.е. , т.е. 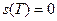 , откуда , откуда 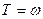 . Поэтому . Поэтому 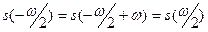 , т.е. , т.е. 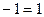 , что невозможно. , что невозможно.
14.
Нулями функции  являются числа вида являются числа вида 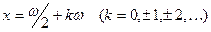 и только эти числа. и только эти числа.
Действительно, согласно тождеству 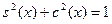 , нулями функции , нулями функции  все те и только те числа все те и только те числа 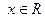 , для которых , для которых 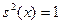 . Последнее же уравнение на отрезке . Последнее же уравнение на отрезке 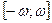 (длина которого равна периоду (длина которого равна периоду 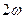 функции функции  ) имеет два решения: ) имеет два решения: 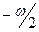 и и 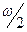 (на основании свойств 2,9,12 и замечания к свойству 12). Для завершения доказательства остаётся воспользоваться свойством 13 и заметить, что полученные две серии решений (на основании свойств 2,9,12 и замечания к свойству 12). Для завершения доказательства остаётся воспользоваться свойством 13 и заметить, что полученные две серии решений
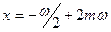 , , 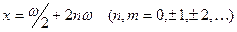
уравнения 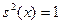 можно объединить в одну: можно объединить в одну:
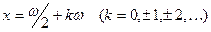 . .
15.
Справедливы следующие тождества (формулы приведения
):
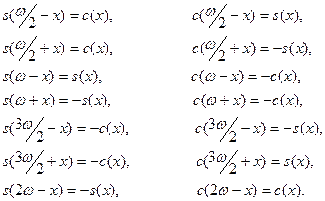
Доказательство. Убедимся, например, что 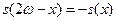 . .
Учитывая свойства 4, 2, замечание к лемме 2 и свойство 3, имеем
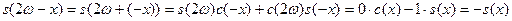 . .
Аналогично убеждаемся в справедливости остальных тождеств.
16.
Наименьший положительный нуль функции  равен равен 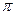 . .
Доказательство. Рассмотрим на координатной плоскости  круг круг 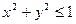 . Его площадь, как известно, равна . Его площадь, как известно, равна 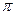 . С другой стороны, эта площадь равна . С другой стороны, эта площадь равна 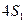 , где , где 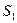 -площадь четверти данного круга, расположенной в первом квадранте. Так как -площадь четверти данного круга, расположенной в первом квадранте. Так как
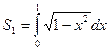 , ,
то
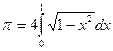
Вводя подстановку 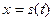 и учитывая, что при возрастании и учитывая, что при возрастании 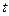 от от 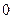 до до 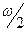 функция функция 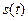 (т.е. (т.е. 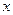 ) возрастает от ) возрастает от 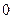 до до 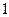 , получаем , получаем
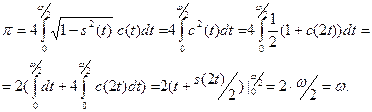
Итак, 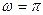 . .
Глава2. Аналитическая теория тригонометрических функций
Функции действительной переменной, представимые в некотором интервале из 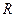 степенными рядами, называются аналитическими
в этом интервале. степенными рядами, называются аналитическими
в этом интервале.
Тригонометрические функции являются аналитическими, т.е. могут быть представлены степенными рядам.
Рассмотрим степенные ряды
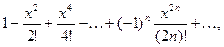 (1) (1)
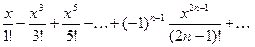 (2) (2)
Эти ряды сходятся, и притом абсолютно, при любом действительном 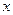 , в чём легко убедиться по признаку Д’Аламбера. Действительно, при любом , в чём легко убедиться по признаку Д’Аламбера. Действительно, при любом 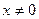
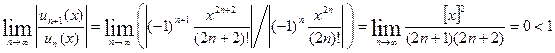 , ,
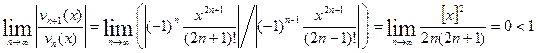 . .
Следовательно, функции 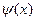 и и 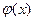 как суммы соответствующих степенных рядов (1) и (2) определены и непрерывны на интервале как суммы соответствующих степенных рядов (1) и (2) определены и непрерывны на интервале 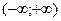 . Более того, эти функции дифференцируемы на . Более того, эти функции дифференцируемы на 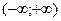 , причём , причём
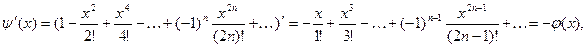
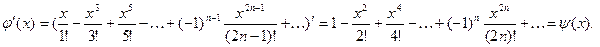
Функция 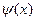 чётная, а чётная, а 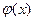 нечётная, так как нечётная, так как 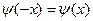 , , 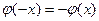 для любого для любого 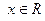 . .
Установим ещё некоторые свойства функций 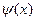 и и 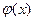 . .
Теорема1.
Для любого действительного 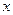
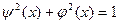 . (3) . (3)
Доказательство.
Имеем
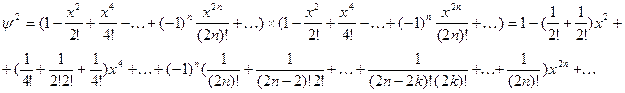
Коэффициент при 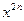 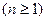 можно представить в виде можно представить в виде
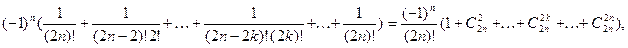 ибо ибо 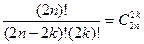 - число сочетаний из - число сочетаний из  элементов по элементов по 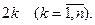
Аналогично
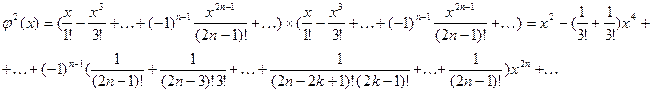
Коэффициент при 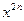  можно представить в виде можно представить в виде
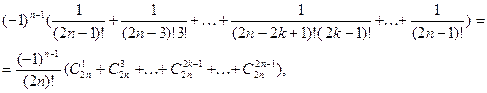
ибо 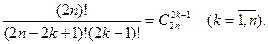
При сложении 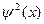 и и 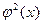 коэффициент при коэффициент при 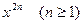 будет равен будет равен

Выражение в скобках равно нулю, в чём можно убедиться, полагая 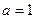 , , 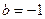 в формуле бинома Ньютона в формуле бинома Ньютона
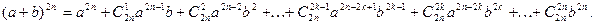
Таким образом, 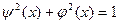 . .
Следствие.
Функции 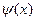 и и 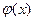 ограниченные, причём ограниченные, причём 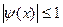 и и 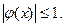
Теорема 2
.
(теорема сложения для функций 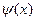 и и 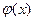 ). Для любых действительных
). Для любых действительных 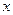 и и 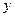
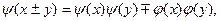 (4) (4)
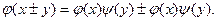 (5) (5)
Доказательство
.
Проверим формулу:
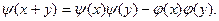
Имеем:
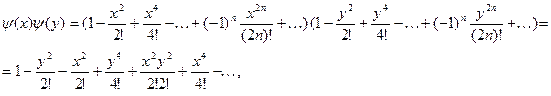
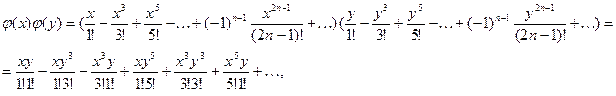
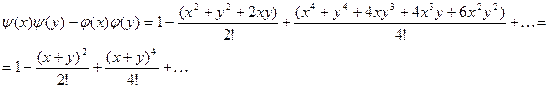
Рассмотрим общий член этого ряда, содержащий произведения вида: 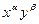 , где , где 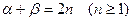 . Получим . Получим
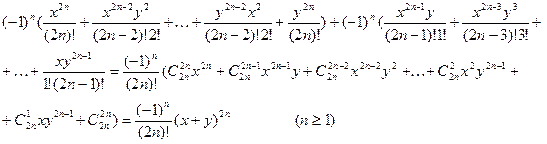
ибо 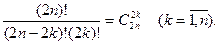
Таким образом,
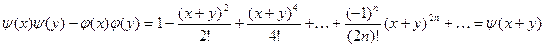 . .
Используя чётность или нечётность функций 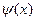 и и 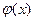 , проверим справедливость формулы: , проверим справедливость формулы:
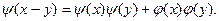
Имеем
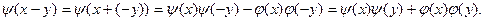
Аналогично проверяется справедливость формул
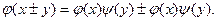
Теорема3.
Для любых действительных
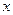 и и 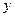 функция функция 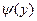 удовлетворяет уравнению удовлетворяет уравнению
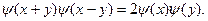 (6) (6)
Доказательство.
По определению функции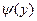 имеем: имеем:
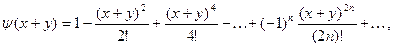
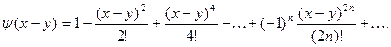
Вычислим 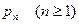 - общий член ряда для суммы - общий член ряда для суммы 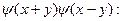
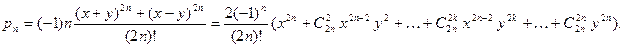
Далее,
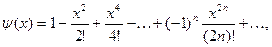
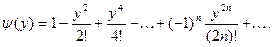
Вычислим 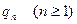 - общий член ряда для произведения - общий член ряда для произведения 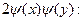
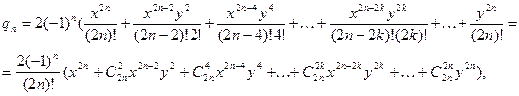
ибо 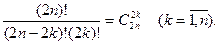 Получим, что Получим, что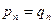 при при 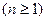 , а поскольку , а поскольку 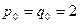 , то при любых действительных , то при любых действительных 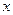 и и 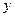 имеет место равенство (6). имеет место равенство (6).
Замечание1.
Из формул сложения (3) и (4) следуют формулы двойного аргумента:
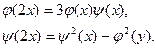 (7) (7)
Замечание2.
Непосредственно из формул (3) и (7) получим:
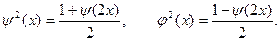
Теорема4.
Ф
ункция 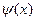 имеет по крайней мере один положительный нуль. имеет по крайней мере один положительный нуль.
Доказательство.
Так как для любого 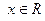
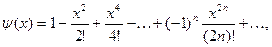
то 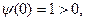
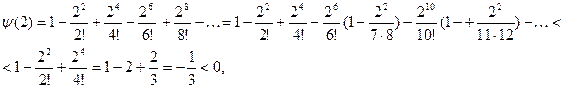
и по теореме о промежуточных значениях непрерывной на отрезке функции 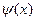 на на 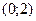 имеет по крайней мере один нуль, т.е. существует число
имеет по крайней мере один нуль, т.е. существует число 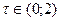 , такое, что , такое, что 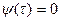 . .
Теперь справедливы следующие утверждения.
1. Функция 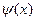 имеет наименьший положительный нуль имеет наименьший положительный нуль 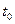 , иными словами, существует , иными словами, существует 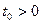 , такое, что , такое, что 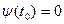 . .
2. Имеют место равенства:
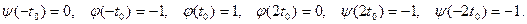
3. Функция 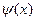 положительна на интервале положительна на интервале 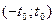 , а функция , а функция 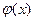 - на интервале - на интервале 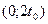 . .
4. Функция 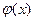 возрастает на отрезке возрастает на отрезке 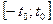 . .
5. Функция 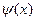 убывает на отрезке убывает на отрезке 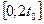 и возрастает на отрезке и возрастает на отрезке 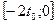 . .
6. 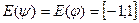 . .
7. Нулями функции 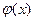 являются числа являются числа 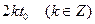 и только такие числа, а функции и только такие числа, а функции 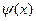 - числа - числа 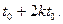
8. Функции 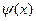 и и 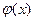 являются периодическими с наименьшим положительным периодом являются периодическими с наименьшим положительным периодом 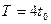 . .
9. Имеют место формулы приведения:
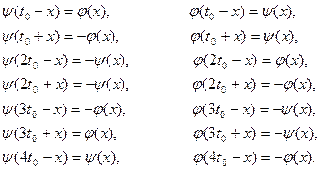
10. Наименьший положительный нуль функции 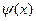 равен равен 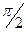 . .
Список литературы
1. Архипов Б.М., Мазаник А.А., Петровский Г.Н., Урбанович М.И., Элементарные функции: Учеб. Пособие.- Мн.: Выш. шк., 1991.-140с.2. Фихтенгольц Г.М., Курс дифференциального и интегрального исчисления: том I-Спб.: Издательство «Лань», 1997.-800с. |