Министерство образования Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Тульский государственный университет»
Кафедра Геоинженерии и Кадастра
КОНТРОЛЬНАЯ РАБОТА
ОСНОВЫ ГЕОДЕЗИИ
Содержание
Задание 1. Определить среднюю квадратическую ошибку угла, измеренного одним полным приемом при помощи теодолита Т-30, учитывая ошибку mо
отсчета по микроскопу при двух наведениях t, визирования mv
и за внецентренность теодолит mc
и вех, если mc
= mr
=15//
+i//
, v=20х
. Принять i равным номеру по журналу.
Задание 2. Оценить точность определения коэффициента дальномера зрительной трубы С, если измерено горизонтальное расстояние от оси вращения трубы до рейки s±ms
и определен отрезок l рейки между дальномерными нитями сетки с ошибкой ml
. Ошибкой в определении слагаемого дальномера можно пренебречь. Принять s=147,83 м±i (см),ms
=± 0,070 м ±(0,000 + i)(м) ;l=1.48м, ml
=±0,0050м. Принять i равным номеру по журналу.
Задание 3. По результатам измерения угла найти вероятнейшее значение угла, средние квадратические ошибки одного измерения и арифметической средины, вероятную ошибку, среднюю ошибку, предельную. Изменить третью, пятую, десятую ошибку по правилу m±0,i//
(табл 1).
Таблица 1.
| Значения углов |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
69о
44/
15//
,5
|
69о
44/
16//
,4 |
69о
44/
15//
,6 |
69о
44/
17//
,0 |
69о
44/
16//
,3 |
69о
44/
18//
,7 |
69о
44/
17//
,3 |
69о
44/
17//
,5 |
69о
44/
17//
,1 |
69о
44/
15//
,7 |
69о
44/
17//
,0 |
69о
44/
15//
,3 |
Задание 4. Уравновесить по способу косвенных измерений результаты нивелирования системы ходов (рис). Вычислить среднюю квадратическую ошибку нивелирования на 1 км хода и произвести оценку точности определения отметок узловых реперов и разности уравновешенных отметок НЕ
-НС
методом весовых коэффициентов по Ганзену. Исходные отметки изменить по правилу Н±0.00(i/3)м.
| № марок |
Отметки Н,м |
| А |
134,836 |
| В |
142,512 |

Рис. Схема нивелирных ходов
| № ходов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| Превышения h,м |
+3,436 |
+4,242 |
+4,176 |
+3,506 |
+2,819 |
-4,866 |
+0,744 |
-1,366 |
| Длины ходов L,км |
8,4 |
7,1 |
3,8 |
4,3 |
6,5 |
2,7 |
5,2 |
3,1 |
Задача 1
Определить среднюю квадратическую ошибку угла, измеренного одним полным приемом при помощи теодолита Т-30, учитывая ошибку mо
отсчета по микроскопу при двух наведениях t, визирования mv
и за внецентренность теодолит mc
и вес, если mc
= mr
=20//
, v=20х
.
Решение:
Найдем ошибки от отдельных источников ошибок. Средняя квадратическая ошибка среднего из отсчетов по двум верньерам
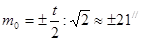 . .
Средняя квадратическая ошибка визирования трубой теодолита
 . .
Суммарная ошибка измеренного одним полуприемом направления найдется по формуле
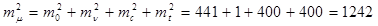 , ,
И  . .
Угол есть разность двух направлений, следовательно,
 , ,
Для среднего значения угла, полученного из двух полуприемов,
 . .
Задача 2
Оценить точность определения коэффициента дальномера зрительной трубы С, если измерено горизонтальное расстояние от оси вращения трубы до рейки s±ms
и определен отрезок l рейки между дальномерными нитями сетки с ошибкой ml
. Ошибкой в определении слагаемого дальномера можно пренебречь. Принять s=147,88 м, ms
=± 0,075 м; l=1.48м, ml
=±0,0050м.
Решение
Логарифмируя функцию  , получаем , получаем

Коэффициент дальномера С будет получен с некоторой ошибкой, вследствии ошибок измерений величин s и l. Эти ошибки вызовут соответствующие ошибки в логарифмах величин s, l, и С, которые обозначим mlgs
, mlgl
, и mlgC
.
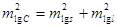 . .
Значение mlgs
, и mlgl
найдем по табличным разностям логарифмов
 Табличная разность равна 3. Табличная разность равна 3.
При изменении s на 0,01 м логарифм s изменяется на 3 единицы последнего знака. При изменении же s на величину  логарифм s изменится на величину, приблизительно в 8 раз большую, то есть логарифм s изменится на величину, приблизительно в 8 раз большую, то есть  единицам 5-го знака логарифма единицам 5-го знака логарифма
Аналогично находим
 Табличная разность равна 30. Табличная разность равна 30.
Здесь при изменении l на 0,01 м логарифм l изменяется на 30 единиц пятого знака, а так как  , то , то 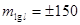 единице 5-го знака логарифма. единице 5-го знака логарифма.
Далее
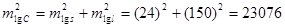 . .
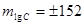 , ,

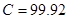 .
.
При изменении С на 0,1 логарифм его изменяется на 44 единицы 5-го знака логарифма. Составит пропорцию  , откуда , откуда 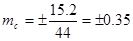 . Эти вычисления записываем в таблицу: . Эти вычисления записываем в таблицу:
| Обозначения величин |
Значения величин |
Изменения |
Средние квадратические ошибки |
m2
lg
|
| величин |
их логарифмов |
величин |
их логарифмов |
| lgs |
2.16991 |
0.01 |
3 |
0.075 |
24 |
576 |
| доп. lgl |
9.82974 |
0.001 |
30 |
0.005 |
150 |
22500 |
| lg C |
1.99965 |
0.1 |
44 |
∑ |
23076 |
| C |
99.92 |
0.35 |
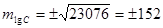 единицы 5-го знака логарифма; единицы 5-го знака логарифма;
 , откуда , откуда  . .
Ответ: 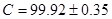 . .
Задача 3
По результатам измерения угла найти вероятнейшее значение угла, средние квадратические ошибки одного измерения и арифметической средины, вероятную ошибку, среднюю ошибку, предельную.
Таблица 1.
| Значения углов |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
69о
44/
15//
,5
|
69о
44/
16//
,4 |
69о
44/
16//
,1 |
69о
44/
17//
,0 |
69о
44/
16//
,8 |
69о
44/
18//
,7 |
69о
44/
17//
,3 |
69о
44/
17//
,5 |
69о
44/
17//
,1 |
69о
44/
16//
,2 |
69о
44/
17//
,0 |
69о
44/
15//
,3 |
Решение:
Решение задачи выполняется в двух вариантах.
Первый вариант:
| №п/п |
l |
ε |
δ |
δ2
|
εδ |
| 0 |
/ |
// |
| 1 |
69 |
44 |
15.5 |
0.2 |
+1.20 |
1.44 |
+0.24 |
| 2 |
16.4 |
1.1 |
+0.30 |
0.09 |
+0.33 |
| 3 |
16.1 |
0.8 |
+0.60 |
0.36 |
+0.48 |
| 4 |
17.0 |
1.7 |
-0.30 |
0.09 |
-0.51 |
| 5 |
16.8 |
1.5 |
-0.10 |
0.01 |
-0.15 |
| 6 |
18.7 |
3.4 |
-2.00 |
4.00 |
-6.80 |
| 7 |
17.3 |
2.0 |
-0.60 |
0.36 |
-1.20 |
| 8 |
17.5 |
2.2 |
-0.80 |
0.64 |
-1.76 |
| 9 |
17.1 |
1.8 |
-0.40 |
0.16 |
-0.72 |
| 10 |
16.2 |
0.9 |
+0.50 |
0.25 |
+0.45 |
| 11 |
17.0 |
1.7 |
-0.30 |
0.09 |
-0.51 |
| 12 |
15.3 |
0.0 |
+1.40 |
1.96 |
0.00 |
| l0
|
69 |
44 |
15.3 |
| [ε]/n |
1.4 |
| x' |
16.7 |
17.3 |
-0.50 |
9.45 |
-10.15 |
 ;
;
 ;
;
 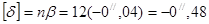 ;
; 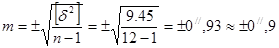 ; ;
 ; ;  . .
Как видим, вследствие ошибок округления контроль сходится весьма приближенно. Можно показать, что этот контроль уточняется следующим образом:
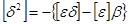 . .
В данном случае
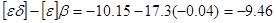 . .
Полученное расхождение с  на 0,01 объясняется приближенностью контрольной формулы. на 0,01 объясняется приближенностью контрольной формулы.
Второй вариант:
| №п/п |
l |
ε" |
ε2
|
δ |
δ2
|
| 0 |
/ |
// |
| 1 |
69 |
44 |
15.5 |
0.2 |
0.04 |
1.20 |
1.44 |
| 2 |
16.4 |
1.1 |
1.21 |
0.30 |
0.09 |
| 3 |
16.1 |
0.8 |
0.64 |
0.60 |
0.36 |
| 4 |
17.0 |
1.7 |
2.89 |
-0.30 |
0.09 |
| 5 |
16.8 |
1.5 |
2.25 |
-0.10 |
0.01 |
| 6 |
18.7 |
3.4 |
11.56 |
-2.00 |
4.00 |
| 7 |
17.3 |
2 |
4 |
-0.60 |
0.36 |
| 8 |
17.5 |
2.2 |
4.84 |
-0.80 |
0.64 |
| 9 |
17.1 |
1.8 |
3.24 |
-0.40 |
0.16 |
| 10 |
16.2 |
0.9 |
0.81 |
0.50 |
0.25 |
| 11 |
17.0 |
1.7 |
2.89 |
-0.30 |
0.09 |
| 12 |
15.3 |
0 |
0 |
1.40 |
1.96 |
| l0
|
69 |
44 |
15.3 |
| [ε]/n |
1.44 |
| x' |
16.70 |
17.3 |
34.37 |
-0.50 |
9.45 |
 ;
;
 ;
;
 ;
;

 ;
;
 ;
;
 .
.
Средняя ошибка:

Вероятная ошибка:
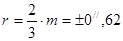 . .
Предельная ошибка:
 . .
Ответ:  . .
Задача 4
Уравновесить по способу косвенных измерений результаты нивелирования системы ходов (рис). Вычислить среднюю квадратическую ошибку нивелирования на 1 км хода и произвести оценку точности определения отметок узловых реперов и разности уравновешенных отметок НЕ
-НС
методом весовых коэффициентов по Ганзену. А=134,838 м, В=142,514 м.
| № ходов |
Превышения h |
Длина ходов L |
| 1 |
3.436 |
8.4 |
| 2 |
4.242 |
7.1 |
| 3 |
4.176 |
3.8 |
| 4 |
3.506 |
4.3 |
| 5 |
2.819 |
6.5 |
| 6 |
-4.866 |
2.7 |
| 7 |
0.744 |
5.2 |
| 8 |
-1.366 |
3.1 |
Решение:
I. Установим в качестве независимых неизвестных отметки узловых реперов С, в и Е и выразим все превышения в функции этих неизвестных. Обозначим вероятнейшие значения отметок HC
, HD
и HE
соответственно через x, y, я и положим
 ,
, 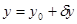 , ,  . .
Вычислим приближенные значения неизвестных:
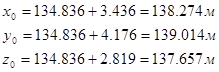
II. Составим уравнения ошибок в общем виде:
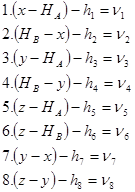
III. Подставив вместо неизвестных их приближенные значения плюс поправки, получим уравнения ошибок с поправками к приближенным значения неизвестных. Свободные члены в этих уравнениях выражаем в сантиметрах:
| 1. |
+ |
= |
 |
| 2. |
- |
-0.2 |
см |
= |
 |
| 3. |
+ |
= |
 |
| 4. |
- |
-0.6 |
см |
= |
 |
| 5. |
+ |
= |
 |
| 6. |
+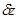 |
+0.9 |
см |
= |
 |
| 7. |
- |
+ |
-0.4 |
см |
= |
 |
| 8. |
- |
+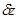 |
+0.9 |
см |
= |
 |
IV. Составим таблицу коэффициентов уравнений ошибок.
| № п/п |
a |
b |
c |
l, см |
s |
p=l/L |
v, см |
pv |
pvv |
plv |
| 1 |
+1 |
+0.0 |
+1 |
0.12 |
-0.26 |
-0.0312 |
0.008 |
0 |
| 2 |
-1 |
-0.2 |
-1.2 |
0.14 |
+0.06 |
+0.0084 |
0.001 |
-0.002 |
| 3 |
+1 |
+0.0 |
+1 |
0.26 |
-0.07 |
-0.0182 |
0.001 |
0 |
| 4 |
-1 |
-0.6 |
-1.6 |
0.23 |
-0.53 |
-0.1219 |
0.065 |
+0.073 |
| 5 |
+1 |
+0.0 |
+1 |
0.15 |
-0.77 |
-0.1155 |
0.089 |
0 |
| 6 |
+1 |
+0.9 |
+1.9 |
0.37 |
+0.14 |
+0.0518 |
0.007 |
+0.047 |
| 7 |
-1 |
+1 |
-0.4 |
-0.4 |
0.19 |
-0.21 |
-0.0399 |
0.008 |
+0.016 |
| 8 |
-1 |
+1 |
+0.9 |
+0.9 |
0.32 |
+0.20 |
+0.0640 |
0.013 |
+0.058 |
| Сумма |
-1 |
0 |
+3 |
+0.6 |
+2.6 |
0.192 |
+0.192 |
| Неизвестные |
-0.260 |
-0.068 |
-0.765 |
Весовая функция по условию задачи имеет вид
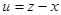
для которой f1
=-1, f2
=0, f3
=+1.
V. Составим таблицу коэффициентов нормальных уравнений (таблица 1).
VI. Выпишем нормальныеуравнения
| 1 |
0.450 |
-0.190 |
+0.104 |
= |
0 |
| 2 |
-0.190 |
+1.000 |
-0.320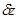 |
-0.226 |
= |
0 |
| 3 |
-0.320 |
+0.840 |
+0.621 |
= |
0 |
| ∑ |
+0.260 |
+0.490 |
+0.520 |
+0.499 |
= |
0 |
Контроль
0.068-0.033-0.398+0.499=0
Этот контроль произведем после решения нормальных уравнений, подставив найденные поправки неизвестных в суммарное уравнение.
VII. Решим нормальные уравнения (таблица 2).
VIII. Вычислим уравновешенные значения превышений.
| № ходов |
Измеренные превышения, м |
Поправки, мм |
Уравновешенные превышения, м |
| 1 |
+3.436 |
-2.6 |
+3.4334 |
| 2 |
+4.242 |
+0.6 |
+4.2426 |
| 3 |
+4.176 |
-0.7 |
+4.1753 |
| 4 |
+3.506 |
-5.3 |
+3.5007 |
| 5 |
+2.819 |
-7.7 |
+2.8113 |
| 6 |
-4.866 |
+1.4 |
-4.8646 |
| 7 |
+0.744 |
-2.1 |
+0.7419 |
| 8 |
-1.366 |
+2.0 |
-1.3640 |
IX. Выполним окончательный контроль всех вычислений
| 1 |
h1
+h7
-h3
= |
0 |
+3.4334 |
+0.7419 |
-4.1753 |
= |
0 |
| 2 |
h2
-h4
-h7
= |
0 |
+4.2426 |
-3.5007 |
-0.7419 |
= |
0 |
| 3 |
h4
+h6
-h8
= |
0 |
+3.5007 |
-4.8646 |
+1.3640 |
= |
0 |
| 4 |
h3
+h8
-h5
= |
0 |
+4.1753 |
-1.3640 |
-2.8113 |
= |
0 |
| 5 |
HA
+h3
+h4
= |
HB
|
134.838 |
_+4.1753 |
+3.5007 |
= |
142.514 |
X. Произведем оценку точности.
1) Средняя квадратическая ошибка единицы веса (превышения по ходу 1 км)
 ; ;
Ошибка самой ошибки единицы веса
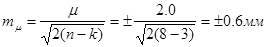 .
.
2) Средние квадратические ошибки высот определяемых реперов

3) Среднюю квадратическую ошибку функции 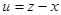 найдем по формуле найдем по формуле

 ;
;
 и
и  . .
Таблица 1
| № п/п |
paa |
pab |
pac |
pal |
pas |
pbb |
pbc |
pbl |
pbs |
pcc |
pcl |
pcs |
pll |
pls |
| 1 |
0.120 |
0.120 |
| 2 |
0.140 |
0.028 |
0.168 |
0.006 |
0.034 |
| 3 |
0.260 |
0.260 |
| 4 |
0.230 |
0.138 |
0.368 |
0.083 |
0.221 |
| 5 |
0.150 |
0.000 |
0.150 |
| 6 |
0.370 |
0.333 |
0.703 |
0.300 |
0.633 |
| 7 |
0.190 |
-0.190 |
0.076 |
0.076 |
0.190 |
-0.076 |
-0.076 |
0.030 |
0.030 |
| 8 |
0.320 |
-0.320 |
-0.288 |
-0.288 |
0.320 |
0.288 |
0.288 |
0.259 |
0.259 |
| Сумма |
0.450 |
-0.190 |
0 |
0.104 |
0.364 |
1.000 |
-0.320 |
-0.226 |
0.264 |
0.840 |
0.621 |
1.141 |
0.678 |
1.177 |
Таблица 2
| № строк |
Название строк |
x |
y |
z |
l |
s |
Контроль |
| 1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
N1
|
|
0.450 |
-0.190 |
0.000 |
0.104 |
0.364 |
0.364 |
| -1 |
| 2 |
C1
|
-2.22222 |
0.4222 |
0.0000 |
-0.2311 |
-0.8089 |
0.8089 |
| 3 |
| 4 |
N2
|
|
1.000 |
-0.320 |
-0.226 |
0.264 |
0.264 |
| 5 |
(1); C1,2
* N1
|
|
-0.080 |
0.000 |
0.044 |
0.154 |
| 6 |
N1
||
|
0.920 |
-0.320 |
-0.182 |
0.418 |
0.418 |
| -1 |
| 7 |
C2
|
-1.087 |
0.3478 |
0.1978 |
-0.4543 |
-0.4543 |
| 8 |
| 9 |
N3
|
|
0.840 |
0.621 |
1.141 |
1.141 |
| 10 |
(1); С1,3
* N1
|
|
0.000 |
0.000 |
0.000 |
| 11 |
(2); С2,3
* N1
||
|
-0.111 |
-0.063 |
0.145 |
| 12 |
N1
|||
|
0.729 |
0.558 |
1.286 |
1.287 |
| -1 |
| 13 |
C3
|
-1.3717 |
-0.7654 |
-1.7641 |
| 14 |
| 15 |
Ci,l
|
-0.231 |
0.198 |
-0.765 |
0.678 |
1.177 |
| 16 |
dz*Ci,3
|
0 |
-0.266 |
dz |
-0.024 |
-0.084 |
| 17 |
dy*Ci,2
|
-0.029 |
-0.068 |
-0.036 |
0.083 |
| 18 |
-0.260 |
dy |
-0.427 |
-0.984 |
| 19 |
dx |
[pvv] |
0.191 |
0.192 |
| 20 |
0 |
1.372 |
| 21 |
3,3) |
0.201 |
0.477 |
Q33
|
| 22 |
3,2) |
0.201 |
Q32
|
| 23 |
3,1) |
Q31
|
| 24 |
1.087 |
| 26 |
0 |
0.166 |
0.477 |
| 27 |
2,3) |
0.529 |
1.253 |
Q23
|
| 28 |
2,2) |
0.529 |
Q22
|
| 29 |
2,1) |
Q21
|
| 30 |
2.222 |
| 31 |
0 |
0.201 |
| 32 |
2,3) |
0.223 |
0.529 |
Q13
|
| 33 |
2,2) |
2.445 |
Q12
|
| 34 |
2,1) |
Q11
|
| 35 |
∑Q |
3.175 |
2.259 |
2.050 |
| 36 |
Si
|
0.260 |
0.490 |
0.520 |
| 37 |
Si∑Q |
0.826 |
1.107 |
1.066 |
2.999 |
3.000 |
|