Курсовая работа: Расчет профиля диффузии сурьмы в кремнии
|
Название: Расчет профиля диффузии сурьмы в кремнии Раздел: Рефераты по физике Тип: курсовая работа | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
АННОТАЦИЯ В данной работе выполнен расчет профилей диффузии сурьмы в кремнии. В основе работы лежало использование феноменологической модели диффузии. Использовалось численное решение уравнения диффузии по неявной разностной схеме. Полученные результаты хорошо согласуются с известными данными из литературы. Полученные таким методом данные могут широко использоваться при расчете необходимой глубины залегания примеси. Объем расчетно-пояснительной записки составляет ___ листа, она содержит 19 рисунков, 2 таблицы, приложение. В работе использовано 7 литературных источников. СОДЕРЖАНИЕ ВВЕДЕНИЕ 1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1.1 Феноменологические модели 1.2 Механизмы диффузии атомов в полупроводниках 1.3 Коэффициент диффузии примесного атома 1.4 Зарядовые состояния точеных дефектов 2 ПРАКТИЧЕСКАЯ ЧАСТЬ ВЫВОДЫ СПИСОК ЛИТЕРАТУРЫ ПРИЛОЖЕНИЕ ВВЕДЕНИЕ Диффузия – один из важнейших технологических процессов при изготовлении любых видов электронных приборов и микросхем, в частности, на кремнии. Диффузия легирующей примеси в полупроводник используется чаще всего для получения p-n перехода. Расчет профилей диффузии очень важен, так как позволяет очень точно определить глубину залегания p-n перехода, установить необходимые параметры проведения процесса для получения нужной глубины. Целью данной работы было рассчитать профили диффузии сурьмы в кремнии, определить основные параметры этого процесса, определить влияние параметров на глубину залегания примеси. 1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Диффузия в жидкости или твёрдом теле есть дискретное термически активированное перемещение атомов или молекул посредством случайных блужданий. Термическая активация необходима для преодоления частицей потенциального барьера между её последовательными положениями. Дискретность означает, что последовательные положения частицы разделены конечным промежутком. «Случайность блужданий» проявляется в том, что направление каждого перемещения не предопределено начальными условиями, то есть положением и направлением предшествующего перемещения.[1] 1.1 Феноменологические модели Феноменологическое описание диффузии основывается на законе Фика и уравнении непрерывности. Закон Фика устанавливает, что плотность диффузионного потока частиц
Коэффициент пропорциональности называется коэффициентом диффузии. Он является локальной характеристикой матрицы и диффузанта одновременно, и может в общем случае зависеть как от концентрации
Закон Фика можно обосновать теоретически методами термодинамики. Именно, плотность потока
Подвижность связана с коэффициентом диффузии соотношением Эйнштейна
Термодинамическая сила равна градиенту химического потенциала примеси
Сам же химический потенциал может быть записан в виде
где
Уравнение непрерывности следует из интегрального баланса диффундирующих частиц в замкнутом объёме
Рис. 1. Баланс диффундирующих частиц Полное число частиц в объёме - вытекания их из объёма - поглощения частиц внутренними стоками с локальной скоростью - генерации частиц внутренними источниками с локальной скоростью - генерации частиц внешним источником с локальной скоростью Уравнение баланса имеет вид
Оно справедливо для любого объёма V. Преобразовав поверхностный интеграл в объёмный с помощью теоремы Остроградского-Гаусса, получим уравнение непрерывности в виде
Или, после подстановки (1) в (8) ,
Внутренние источники и стоки часто можно считать точечными объектами, распределёнными с концентрациями
где
с начальными условиями
Таким образом, в этом случае следует решать систему уравнений (8), (12), (13). Конкретный вид слагаемых, описывающих изменения концентраций внутренних источников и стоков, определяется физическими механизмами взаимодействия их с диффундирующими частицами. Например, в полупроводниках возможна ситуация, когда сток, захвативший диффузант, превращается в источник, который, после высвобождения диффузанта, снова превращается в сток. В этом случае
Уравнения (8) и (9) принимают вид
Если внутренние источники и стоки подвижны, то в уравнения (16) и (17) следует добавить слагаемые, описывающие их диффузию и дрейф,
Уравнения (9), (18) и (19) необходимо дополнить граничными условиями на свободной границе с вакуумом и границах раздела контактирующих сред различной физической природы. Если через свободную поверхность
Если производится диффузия примеси из заданного начального распределения
На границе раздела
и условие соответствия концентраций
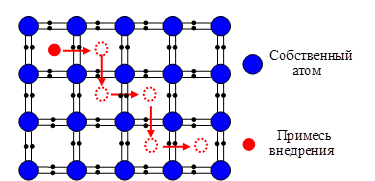
где 1.2 Механизмы диффузии атомов в полупроводниках В кристаллических полупроводниках диффундируют собственные и примесные атомы. Диффузия собственных атомов называется самодиффузией, диффузия примесных атомов - примесной диффузией. Назовём регулярным положением атома в кристалле то, в котором он проявляет присущие ему предназначение и свойства. Регулярные положения собственных атомов – в узлах кристаллической решётки. Для примесных атомов регулярными могут быть как узлы, так и междуузлия. В узлах располагаются примеси, создающие мелкие донорные и акцепторные центры - Примеси внедрения малого радиуса диффундируют по прямому междуузельному механизму. Это значит, что они совершают переход или акт миграции, или скачок, непосредственно из одного междуузлия в другое (рис. 2).
Рис. 2. Прямой междуузельный механизм диффузии Коэффициент диффузии
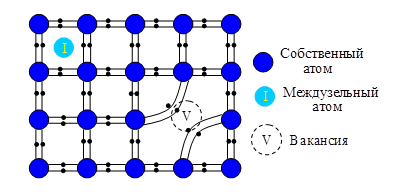
где Собственные атомы и примеси замещения диффундируют при посредстве элементарных точечных дефектов кристаллической решётки – вакансий
Рис. 3. Вакансия Вакансии и собственные междуузельные атомы являются необъемлемой подсистемой кристалла. В состоянии термодинамического равновесия они образуются по механизму Шоттки – при переходе атома из узла в объёме на поверхность создаётся вакансия, при переходе собственного атома с поверхности в объём создаётся междуузельный атом. Концентрации равновесных точечных дефектов
При По соседству с вакансиями и междуузельными атомами всегда имеются занятые узлы решётки или свободные междуузлия, в которые можно совершить скачок, поэтому подвижность их очень высока. Они совершают термически активированные случайные блуждания, преодолевая потенциальные барьеры между своими регулярными положениями. Роль точечных дефектов в диффузии примесей замещения заключается в следующем. Примесный атом Если подвижный комплекс включает вакансию, то говорят, что диффузия идёт по вакансионному механизму. Образование и распад примесно-вакансионного комплекса описывается квазихимической реакцией
Исчезновение комплекса происходит по реакции
Физически комплекс
Рис. 4. Вакансионный механизм диффузии Если в состав подвижного комплекса входит собственный междуузельный атом Выделяют три разновидности междуузельного механизма диффузии: - парный междузельный механизм описывается квазихимической реакцией
- механизм вытеснения описывается квазихимической реакцией
Символ - диссоциативный механизм, или механизм Франка-Тэрнбала описывается квазихимическими реакциями
Примесный атом замещения переходит в междуузельную позицию самостоятельно, вследствие теплового движения, в результате образуется примесно-междуузельный комплекс и вакансия, далее диффундирующие независимо. Наглядная модель диффузионных скачков по междуузельному механизму показана на рис.5.
Рис. 5. Междуузельный механизм диффузии Исчезновение примесно-междуузельного комплекса происходит по реакции
1.3 Коэффициент диффузии примесного атома Если бы все примесные атомы
В общем случае примесь замещения
Парциальные коэффициенты диффузии
Здесь Тогда В состоянии термодинамического равновесия
Относительный вклад каждого механизма характеризуют параметрами
Они связаны естественным соотношением
Концентрации подвижных комплексов тем больше, чем больше концентрации междуузельных атомов
Тогда коэффициент диффузии при произвольных неравновесных концентрациях
Неравновесные точечные дефекты можно создать различными методами. Например, междуузельные атомы инжектируются в кремний при его окислении, а вакансии – при азотировании. Измеряя в таких экспериментах 1. Элементы III группы 2. В IV группе наблюдается переход от междуузельного механизма к вакансионному с возрастанием атомного радиуса:
3. Та же тенденция наблюдается в V группе:
Поскольку и коэффициенты диффузии точечных дефектов, и концентрации примесно-дефектных комплексов активируются термически, то температурные зависимости парциальных коэффициентов диффузии можно аппроксимировать аррениусовскими законами
где 1.4 Зарядовые состояния точеных дефектов Изложенная атомная модель диффузии должна быть обобщена, чтобы учесть тот факт, что точечные дефекты могут находиться в нескольких зарядовых состояниях. Каждое зарядовое состояние независимо вносит вклад в диффузию примеси, при этом аррениусовские параметры у них различны. Рассмотрим сначала вакансии. Установлено, что вклад в диффузию примесей вносят в основном пять зарядовых состояний – нейтральноу Равновесные концентрации заряженных вакансий определяются положениями их энергетических уровней Концентрация нейтральных вакансий Формулы для них приведены в практической части. Можно получить
2 ПРАКТИЧЕСКАЯ ЧАСТЬ Задание: Методом численного решения одномерного уравнения диффузии необходимо исследовать зависимость профиля концентрации Sb в кремний при диффузии из поверхностного источника постоянной концентрации N0 от парциальных вкладов различных зарядовых состояний точечных дефектов в коэффициент диффузии в интервалах температур и концентраций: 850 ˚С ≤ Т ≤ 1200 ˚С 1015 см-3 ≤ N0 ≤ 1021 см-3. Для расчетов будем использовать программу Mathcad 11. Для построения профилей концентрации легирующей примеси необходимо определить величину коэффициента диффузии, а также его зависимость от температуры и концентрации примеси в поверхностном источнике. Диффузия сурьмы будет идти практически стопроцентно по вакансионному механизму [1], так как сурьма – элемент пятой группы и относительный вклад междоузельного механизма составляет порядка 1%. Коэффициент диффузии будем рассчитывать по уравнению (44). Сурьма – донорная примесь, она будет диффундировать только по нейтральным и отрицательно заряженным вакансиям. Кроме того, двукратно отрицательно заряженные дефекты в силу их незначительного влияния можно не учитывать. Таким образом, выражение для коэффициента диффузии примет вид:
Согласно уравнению Аррениуса:
Т.о. Аррениусовские параметры приведены в табл. 1 [1]: Таблица 1. Аррениусовские параметры Sb в Si [3]
То есть для определения коэффициента диффузии необходимо знать зависимость положения уровня Ферми от температуры. Для его определения воспользуемся уравнением электронейтральности:
В данном уравнении вкладом слагаемого Введем обозначение Концентрации электронов и дырок можно выразить через концентрацию собственных носителей.
Концентрации заряженных дефектов также являются функциями температуры:
Аналогично находим:
Поскольку акцепторные энергетические уровни заряженных дефектов жёстко привязаны к дну зоны проводимости
Совершенно аналогично для междоузельных атомов:
Также находим
Подставляя эти величины в выражения для концентрации заряженных дефектов, а их, в свою очередь в уравнение электронейтральности, получаем уравнение вида:
Из него мы определяем х. Коэффициенты А, В, С и P имеют вид:
В эти выражения входят равновесные концентрации вакансий и междоузлий, которые можно определить из (25). Температурную зависимость для ширины запрещенной зоны определяет соотношение Варшни:
Для кремния

Рис. 6. Зависимость коэффициента диффузии от обратной температуры Решая это уравнение и записывая коэффициент диффузии как
где EF – решение уравнения, получаем зависимости рис. 6. Увеличивая масштаб, получим:

Рис. 7. Зависимость коэффициента диффузии от обратной температуры в увеличенном масштабе

Рис. 8. Зависимость коэффициента диффузии от обратной температуры в полулогарифмическом масштабе Зависимость в полулогарифмическом масштабе от обратной температуры приведена на рис. 8. Увеличивая масштаб:

Рис. 9. Зависимость коэффициента диффузии от обратной температуры в полулогарифмическом увеличенном масштабе
Рис. 10. Зависимость коэффициентов диффузии различных примесей в Si от обратной температуры[5] Полученные зависимости подтверждают предполагаемую многими авторами зависимость D(T) = D0exp(-ΔE/kT). Сравнивая данную зависимость с практическими результатами (рис. 10), например из [5], видим, что сходство теоретических и практических данных очень хорошее. Данные для сурьмы здесь приведены для максимальной поверхностной концентрации 1019 см-3 по работе [6]. Зависимость от концентрации в логарифмическом масштабе (рис. 11):

Рис. 11. Зависимость коэффициента диффузии от концентрации доноров в логарифмическом масштабе Такое поведение графиков можно объяснить тем, что при концентрации доноров меньшей собственной концентрации, имеющей порядок 1020-1021 см-3, ее вклад практически не влияет на коэффициент диффузии. При сравнивании их по порядку, влияние начинает заметно проявляться. Когда же концентрация доноров становится большей на порядок, коэффициент диффузии начинает расти очень быстро. К слову Для определения начала нелинейного участка, найдем производные коэффициента диффузии по концентрации (рис. 12). Как видно из полученных зависимостей коэффициент диффузии не зависит от концентрации доноров до следующих значений концентрации (табл. 2).
 б
б
 г
г

Рис. 12. Зависимость производной коэффициента диффузии от концентрации доноров при: а – 1123 К, б – 1223 К, в – 1323 К, г – 1423 К, д – 1473 К Таблица 2. Пределы начала нелинейности в зависимости коэффициента диффузии
Т.о., в этих диапазонах можно решать уравнение Фика в приближении отсутствия зависимости коэффициента диффузии от температуры. Видно, что с ростом температуры поверхностная концентрация, необходимая для начала нелинейной зависимости коэффициента диффузии, немного растет. Это означает, что при более высоких температурах, коэффициент диффузии становится менее чувствительным к примеси. Это можно объяснить тем, что при повышении температуры увеличивается количество и вакансий, и междоузлий, но количество междоузлий растет быстрее, а примесь по ним перемещается медленнее. Возможно также, что отношение созданной концентрации к собственной при более низкой температуре больше, чем при более высокой, т.е. Предельная растворимость сурьмы в кремнии составляет Максимальная погрешность такого решения по коэффициенту диффузии составит (для 1473 К):
то есть все найденные решения будут удовлетворять условию, чтобы погрешность не превышала 5%. Далее покажем погрешность глубины залегания примеси, при расчете методом постоянного коэффициента диффузии. Отметим сразу, что собственная концентрация при выбранном диапазоне температур превышает Пусть диффузия ведется на глубину 10 мкм. Зададим четыре температуры процесса (1173 К, 1273 К, 1373 К и 1473 К) и сравним полученные профили концентрации в этом случае на пятом временном слое. Выбранное t составляет полчаса. Для этого решим уравнение диффузии:
где Полный текст программы приведен в приложении 1. Для расчетов будем использовать программу, учитывающую непостоянство коэффициента диффузии.

Рис. 13. Профиль распределения примеси при разных температурах диффузии (время процесса – 2,5 часа,
ND
= 1019 см-3, температуры Как видно из полученных распределений (рис. 13) увеличение температуры значительно ускоряет диффузию, что проявляется в увеличении глубины залегания примеси. Из графика видно, что при температуре 1173 К концентрация примеси на глубине 0,1 мкм достигает значения 1010 см-3 за 2,5 часа, в то время как при 1473 К та же концентрация за то же время наблюдается на глубине 6 мкм. То есть целесообразно повышать температуру диффузии, это дает существенную экономию времени. Посмотрим, как влияет на диффузию изменение поверхностной концентрации (рис.14). Пусть температура процесса Т=1473 К. Тогда возможные распределения концентрации (поверхностные концентрации 1018 см-3, 1019 см-3, 2*1019 см-3):

Рис. 14. Профиль распределения примеси при разных поверхностных концентрациях (время процесса – 0,5; 2,5; 5 часов, ND = 1018 см-3, ND = 1019 см-3, ND = 2*1019 см-3, температура 1473 К) Обозначение на графике: - - - - - - - - Очевидно, что чем больше поверхностная концентрация в источнике, тем большая концентрация доноров будет в распределении, и тем глубже будет лежать p-n-переход. Исходя из зависимостей, при поверхностной концентрации 2*1019 см-3 за 5 часов концентрация 1010 см-3 достигается на глубине 7,7 мкм, а за 2,5 часа на глубине 6,2 мкм. Концентрация же в 1 см-3 при 5-часовом процессе и поверхностной концентрации 2*1019 см-3 достигается на глубине 13,3 мкм (рис. 15).
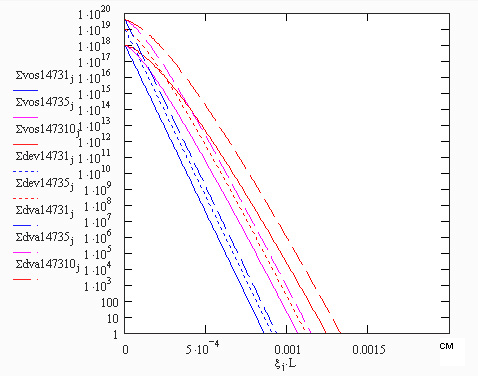
Рис. 15 Профиль распределения примеси при разных поверхностных концентрациях (время процесса – 0,5; 2,5; 5 часов, ND = 1018 см-3, ND = 1019 см-3, ND = 2*1019 см-3, температура 1473 К) в уменьшенном масштабе Построим зависимость для температуры 1473 К и поверхностной концентрации 1019 см-3 и посмотрим, как примесь диффундирует во времени (рис. 16). Из зависимости видно, что при данных условиях, для достижения1010 см-3 на требуемой глубине в 10 мкм требуется проводить процесс более 10 часов. За 10 часов на глубине в 10 мкм будем иметь концентрацию доноров в 2*106 см-3, а за полчаса – 10-3 см-3.

Рис. 16. Эволюция профиля распределения примеси (время процесса – Покажем максимальную погрешность при использовании постоянного коэффициента диффузии и учета его непостоянства (рис. 17):

Рис. 17. Погрешность определения профиля диффузии Здесь Видно, что при проведении процесса в течении 5 часов погрешность на почти 10 мкм при концентрации в 10-6 см-3 составит не более 60 Å, что допустимо даже для самого современного уровня производства. Это говорит о том, что для данной примеси можно вести расчет в предположении постоянства коэффициента диффузии. Также интересно посмотреть на влияние на профиль вклада в коэффициент диффузии отрицательно заряженных дефектов. Для этого исключим из уравнения (45) второе слагаемое. Тогда получим (рис. 18):
Рис. 18. Сравнительная зависимость коэффициентов диффузии от температуры в полулогарифмическом масштабе с учетом и без учета отрицательно заряженных дефектов Как видно из графиков, отрицательно заряженные дефекты вносят весьма существенный вклад в скорость диффузии, без ее учета коэффициент диффузии может падать почти на порядок. Покажем как будут отличаться диффузионные профили в отсутствии этого вклада на рис. 19.
Рис. 19. Сравнение профилей диффузии с учетом и без учета отрицательно заряженных дефектов (время 2,5 часа, температура 1473 К, ND = 2*1019 см-3 ) Как видно, ошибка при таком вычислении при 1473 К, 2,5-часовом процессе и ND = 2*1019см-3 достигает почти 50%, то есть влиянием этого вклада пренебрегать никак нельзя. ВЫВОДЫ В ходе работы была промоделирована диффузия сурьмы в кремний. Также теоретически были определены основные параметры этого процесса: коэффициент диффузии, его зависимость от температуры и поверхностной концентрации примеси, определены температурные зависимости для концентраций дефектов в кремнии. Проведено сравнение полученных температурных зависимостей коэффициента диффузии с практическими. Сходимость результатов найдена очень хорошей. Это говорит о довольно точном значении аррениусовских коэффициентов. Определены пределы начала нелинейности коэффициента диффузии в зависимости от поверхностной концентрации. Было выяснено, что максимальная предельная растворимость сурьмы в кремнии ( Предложено объяснение нелинейного поведения коэффициента диффузии в зависимости от поверхностной концентрации. Рассчитаны диффузионные профили для различных значений температуры, поверхностной концентрации и времени процесса. Также приведена эволюция профиля диффузии во времени. Определены точные значения времени процесса для проникновения примеси на необходимую толщину. Показано, что для ускорения процесса необходимо выбирать как можно большие значения поверхностной концентрации и температуры (2*1019 см-3 при 1473 К). Также показано, что для сурьмы концентрация примеси ни при каких температурах не может превысит собственную концентрацию (например, Проанализирован вклад отрицательно заряженных дефектов в скорость распространения примеси и выяснено, что погрешность при пренебрежении этим вкладом в рассчитанных профилях может достигать 50%, то есть вести расчет без учета этого слагаемого недопустимо. СПИСОК ЛИТЕРАТУРЫ 1. Головатый Ю.П., Косушкин В.Г. Ионная имплантация и диффузия. Методические указания к выполнению курсовой работы по дисциплине «Математическое моделирование технологических процессов». – Калуга, 2007 2. Fahey P. M., Griffin P. B. and Plummer J. D. Rev. Mod. Phys.. - v. 61, 1989. - p.289 3. Van Vechten J.A. Handbook on Semiconductors, edited by T. S. Moss, vol. 3: Materials, Properties and Preparation, ed. S. P. Keller. - North-Holland, New York, 1980. - p. 1 4. http://ioffe.ru 5. Мазель Е.З., Пресс Ф.П. Планарная технология кремниевых приборов. – М.: Энергия, 1974. – 384 с. 6. Fuller, Ditzenberger // J. Appl. Phys, 1954, v. 25, p. 1439-1440; 1956, v. 27, p. 544-553 7. Бургер Р, Донован Р. Окисление, диффузия, эпитаксия. – М.: Мир, 1969 |
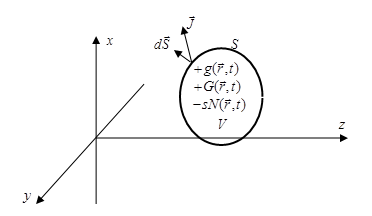

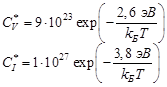 (25)
(25)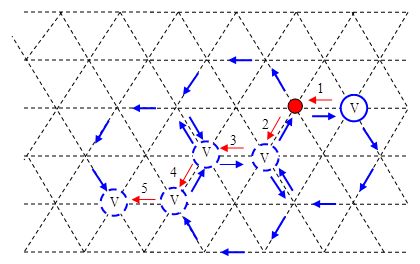

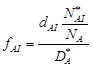 (34)
(34)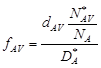 (35)
(35)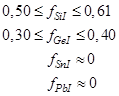
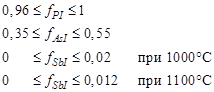
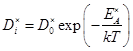 (46)
(46)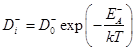 , (47)
, (47)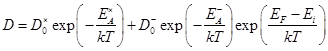 (48)
(48)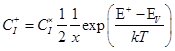 (56)
(56)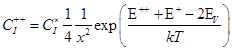 (57)
(57)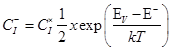 .(58)
.(58)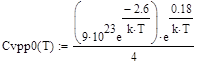 , (71)
, (71)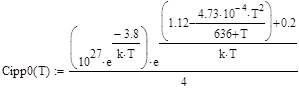 , (72)
, (72)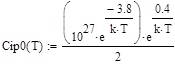 , (73)
, (73) , (74)
, (74) , (75)
, (75)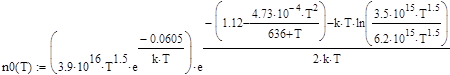 , (76)
, (76)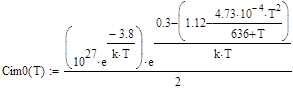 , (77)
, (77)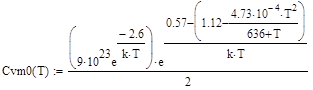 , (78)
, (78)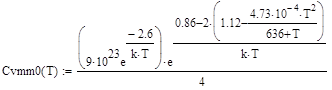 . (79)
. (79)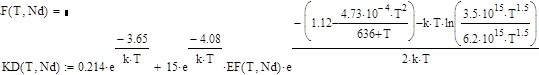 (81)
(81)
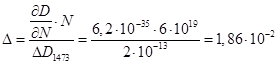 ,(82)
,(82)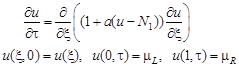 (83)
(83)
